2021-2022学年人教版 九年级上册 23.2.1 中心对称 同步练习(word含答案)
文档属性
| 名称 | 2021-2022学年人教版 九年级上册 23.2.1 中心对称 同步练习(word含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 283.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 16:56:16 | ||
图片预览


文档简介
人教版2021年九年级上册:23.2.1 中心对称 同步练习
一、选择题
1.下列四组图形中,左边的图形与右边的图形成中心对称的有 ( )
A.1组 B.2组 C.3组 D.4组
2.若线段AB与线段CD(与AB不在同一条直线上)关于点O成中心对称,则AB和CD的关系是( )
A.AB=CD B.AB∥CD
C.AB平行且等于CD D.不确定
3.如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是 ( )
A.A与A'是对称点 B.BO=B'O
C.AB∥A'B' D.∠ACB=∠C'A'B'
4.如图,在?ABCD中,对角线AC,BD相交于点O,则图中成中心对称的三角形共有 ( )
A.4对 B.3对 C.2对 D.1对
5.如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是 ( )
A.1或4 B.2或3
C.3或4 D.1或2
6.如图,△ABC与△A'B'C'关于点O成中心对称,ED是△ABC的中位线,E'D'是△A'B'C'的中位线.已知BC=6,则E'D'=( )
A.1 B.3 C.4 D.6
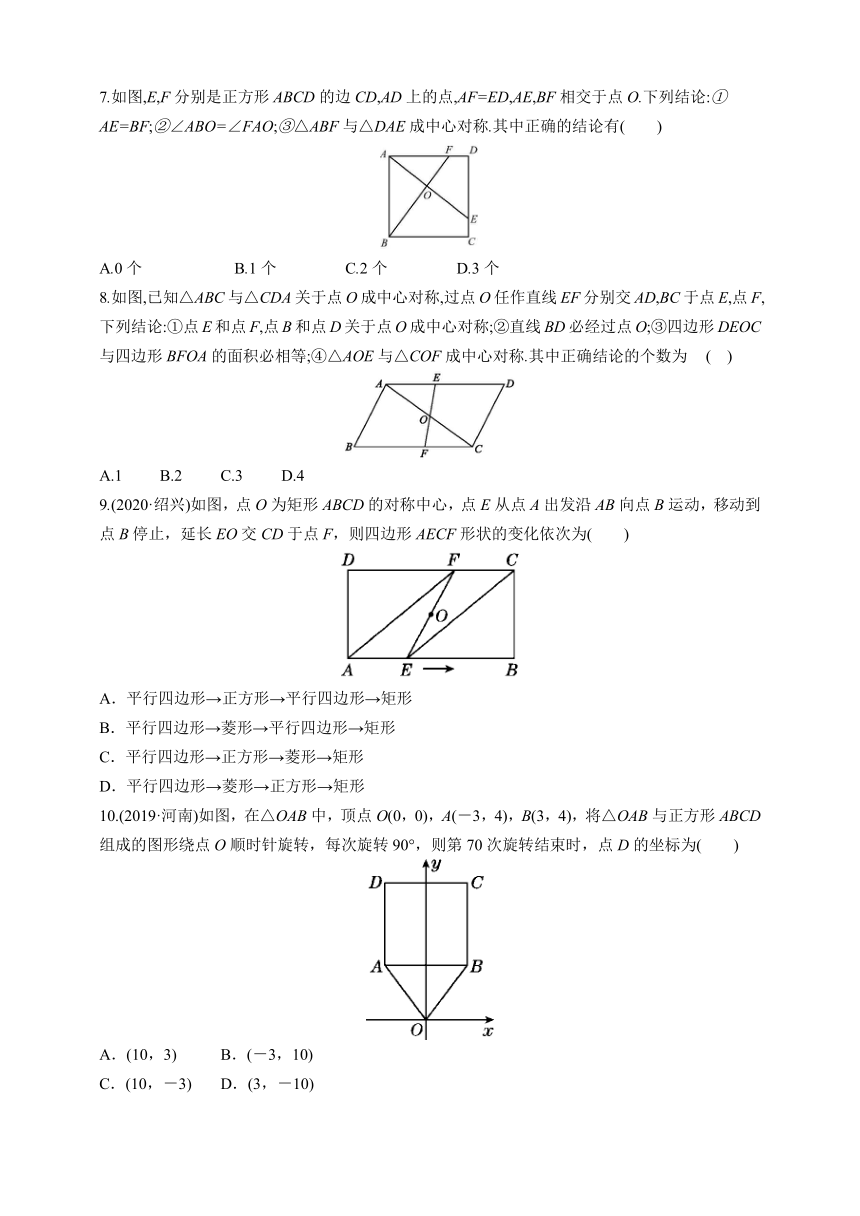
7.如图,E,F分别是正方形ABCD的边CD,AD上的点,AF=ED,AE,BF相交于点O.下列结论:①AE=BF;②∠ABO=∠FAO;③△ABF与△DAE成中心对称.其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
8.如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,点F,下列结论:①点E和点F,点B和点D关于点O成中心对称;②直线BD必经过点O;③四边形DEOC与四边形BFOA的面积必相等;④△AOE与△COF成中心对称.其中正确结论的个数为 ( )
A.1 B.2 C.3 D.4
9.(2020·绍兴)如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
10.(2019·河南)如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为( )
A.(10,3) B.(-3,10)
C.(10,-3) D.(3,-10)
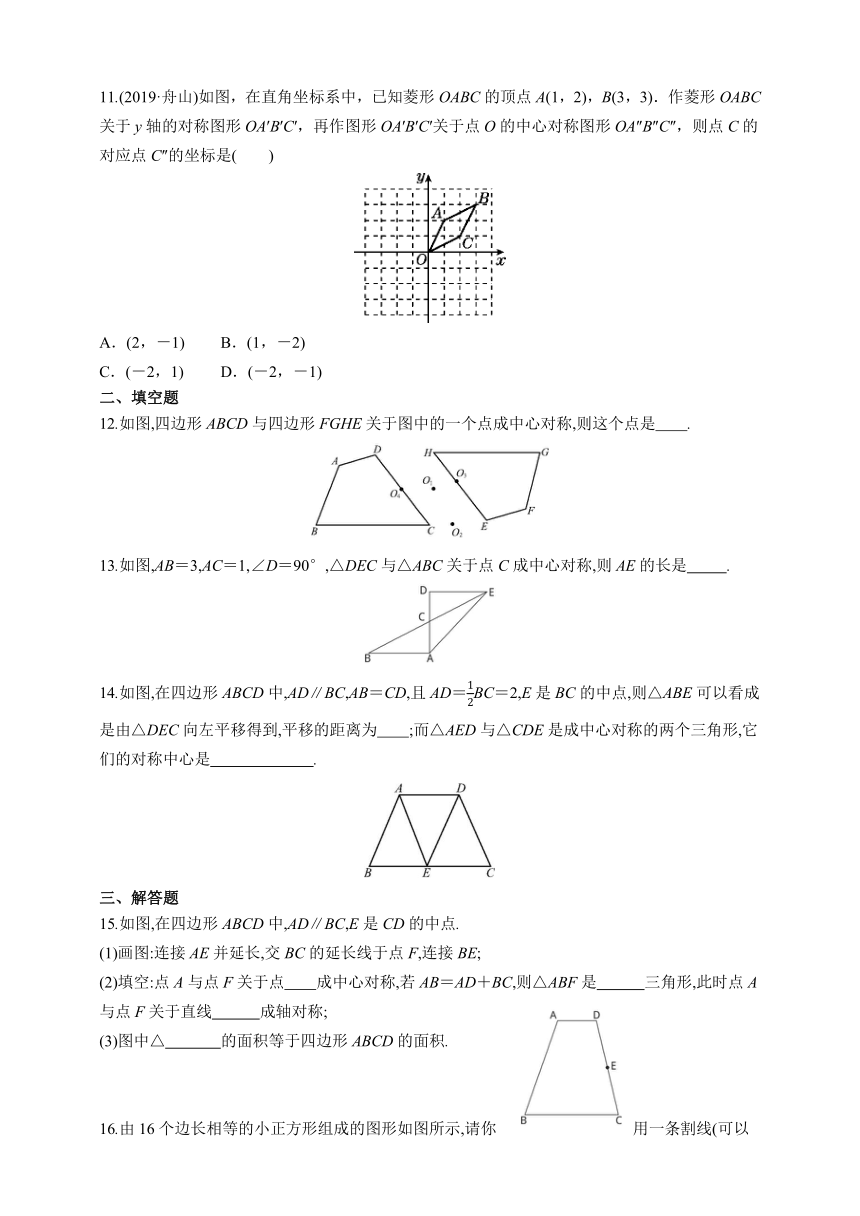
11.(2019·舟山)如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA′B′C′,再作图形OA′B′C′关于点O的中心对称图形OA″B″C″,则点C的对应点C″的坐标是( )
A.(2,-1) B.(1,-2)
C.(-2,1) D.(-2,-1)
二、填空题
12.如图,四边形ABCD与四边形FGHE关于图中的一个点成中心对称,则这个点是 .?
13.如图,AB=3,AC=1,∠D=90°,△DEC与△ABC关于点C成中心对称,则AE的长是 .?
14.如图,在四边形ABCD中,AD∥BC,AB=CD,且AD=12BC=2,E是BC的中点,则△ABE可以看成是由△DEC向左平移得到,平移的距离为 ;而△AED与△CDE是成中心对称的两个三角形,它们的对称中心是 .?
三、解答题
15.如图,在四边形ABCD中,AD∥BC,E是CD的中点.
(1)画图:连接AE并延长,交BC的延长线于点F,连接BE;
3700780364490(2)填空:点A与点F关于点 成中心对称,若AB=AD+BC,则△ABF是 三角形,此时点A与点F关于直线 成轴对称;?
(3)图中△ 的面积等于四边形ABCD的面积.?
16.由16个边长相等的小正方形组成的图形如图所示,请你用一条割线(可以是折线)将它分割成两个图形,使之关于某一点成中心对称,要求给出两种不同的方法.
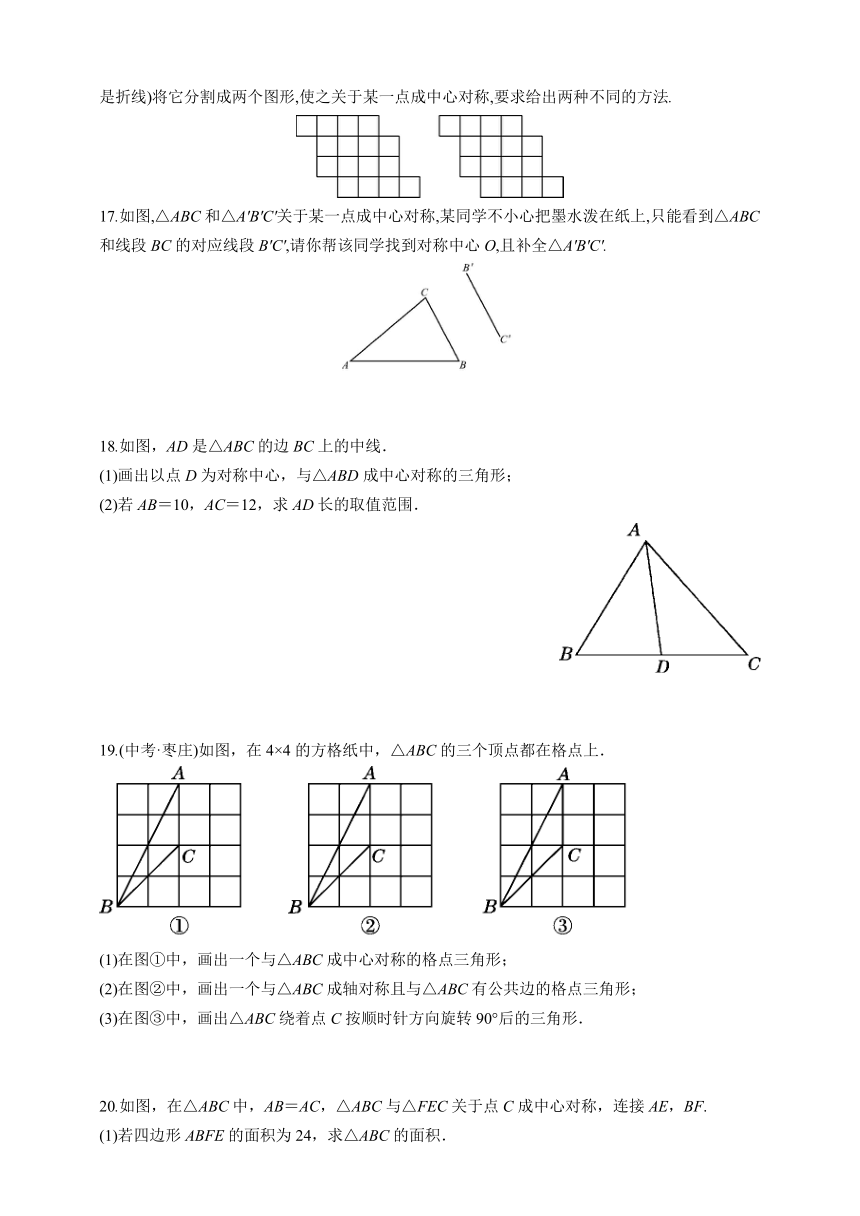
17.如图,△ABC和△A'B'C'关于某一点成中心对称,某同学不小心把墨水泼在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
18.如图,AD是△ABC的边BC上的中线.
(1)画出以点D为对称中心,与△ABD成中心对称的三角形;
(2)若AB=10,AC=12,求AD长的取值范围.
19.(中考·枣庄)如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图①中,画出一个与△ABC成中心对称的格点三角形;
(2)在图②中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;
(3)在图③中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.
20.如图,在△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF.
(1)若四边形ABFE的面积为24,求△ABC的面积.
(2)当∠ACB为多少度时,四边形ABFE为矩形?并说明理由.
21.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,-1),B(-1,-4),C(-3,-4).
(1)作出△A1B1C1,使△A1B1C1与△ABC关于y轴成轴对称图形;
(2)作出与△ABC关于原点成中心对称的图形△A2B2C2,并求出△A2B2C2的面积.
22.课外兴趣小组活动时,老师提出了如下问题:
如图1,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形的三边关系可得2感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
解决问题:受到上述的启发,请你证明下列命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
(1)求证:BE+CF>EF;
(2)若∠A=90°,探索线段BE,CF,EF之间的等量关系,并加以证明.
参考答案
一、选择题
1.下列四组图形中,左边的图形与右边的图形成中心对称的有 (C)
A.1组 B.2组 C.3组 D.4组
2.若线段AB与线段CD(与AB不在同一条直线上)关于点O成中心对称,则AB和CD的关系是(C)
A.AB=CD B.AB∥CD
C.AB平行且等于CD D.不确定
3.如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是 (D)
A.A与A'是对称点 B.BO=B'O
C.AB∥A'B' D.∠ACB=∠C'A'B'
4.如图,在?ABCD中,对角线AC,BD相交于点O,则图中成中心对称的三角形共有 (A)
A.4对 B.3对 C.2对 D.1对
5.如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是 (D)
A.1或4 B.2或3
C.3或4 D.1或2
6.如图,△ABC与△A'B'C'关于点O成中心对称,ED是△ABC的中位线,E'D'是△A'B'C'的中位线.已知BC=6,则E'D'=( B )
A.1 B.3 C.4 D.6
7.如图,E,F分别是正方形ABCD的边CD,AD上的点,AF=ED,AE,BF相交于点O.下列结论:①AE=BF;②∠ABO=∠FAO;③△ABF与△DAE成中心对称.其中正确的结论有( C )
A.0个 B.1个 C.2个 D.3个
8.如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,点F,下列结论:①点E和点F,点B和点D关于点O成中心对称;②直线BD必经过点O;③四边形DEOC与四边形BFOA的面积必相等;④△AOE与△COF成中心对称.其中正确结论的个数为 (D)
A.1 B.2 C.3 D.4
9.(2020·绍兴)如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( B )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
10.(2019·河南)如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为( )
A.(10,3) B.(-3,10)
C.(10,-3) D.(3,-10)
【点拨】∵A(-3,4),B(3,4),∴AB=3+3=6.
∵四边形ABCD为正方形,∴AD=AB=6.
∴D(-3,10).
∵每4次一个循环,70=4×17+2,
∴第70次旋转结束时,相当于将△OAB与正方形ABCD组成的图形绕点O顺时针旋转2次,每次旋转90°.
∴所求点D的坐标为(3,-10).
【答案】D
11.(2019·舟山)如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA′B′C′,再作图形OA′B′C′关于点O的中心对称图形OA″B″C″,则点C的对应点C″的坐标是( A )
A.(2,-1) B.(1,-2)
C.(-2,1) D.(-2,-1)
二、填空题
12.如图,四边形ABCD与四边形FGHE关于图中的一个点成中心对称,则这个点是 O1 .?
13.如图,AB=3,AC=1,∠D=90°,△DEC与△ABC关于点C成中心对称,则AE的长是?13 .?
14.如图,在四边形ABCD中,AD∥BC,AB=CD,且AD=12BC=2,E是BC的中点,则△ABE可以看成是由△DEC向左平移得到,平移的距离为 2 ;而△AED与△CDE是成中心对称的两个三角形,它们的对称中心是 DE的中点 .?
三、解答题
15.如图,在四边形ABCD中,AD∥BC,E是CD的中点.
(1)画图:连接AE并延长,交BC的延长线于点F,连接BE;
(2)填空:点A与点F关于点 E 成中心对称,若AB=AD+BC,则△ABF是 等腰 三角形,此时点A与点F关于直线 BE 成轴对称;?
(3)图中△ ABF 的面积等于四边形ABCD的面积.?
解:(1)图略.
16.由16个边长相等的小正方形组成的图形如图所示,请你用一条割线(可以是折线)将它分割成两个图形,使之关于某一点成中心对称,要求给出两种不同的方法.
解:如图所示.(答案不唯一)
17.如图,△ABC和△A'B'C'关于某一点成中心对称,某同学不小心把墨水泼在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
解:如图所示,BB',CC'的交点即为O,△A'B'C'即为所求.
18.如图,AD是△ABC的边BC上的中线.
(1)画出以点D为对称中心,与△ABD成中心对称的三角形;
解:延长AD至E,使DE=AD,
连接CE,则△ECD即为所求,如图所示.
(2)若AB=10,AC=12,求AD长的取值范围.
解:由(1)知AD=DE,EC=AB=10.
在△ACE中,由AC-EC可得12-10又∵AE=2AD,∴2<2AD<22.
∴119.(中考·枣庄)如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图①中,画出一个与△ABC成中心对称的格点三角形;
解:如图①,△DEC为所求作的三角形.(答案不唯一)
(2)在图②中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;
解:如图②,△ADC为所求作的三角形.
(答案不唯一)
(3)在图③中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.
如图③,△DEC为所求作的三角形.
20.如图,在△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF.
(1)若四边形ABFE的面积为24,求△ABC的面积.
【思路点拨】利用特殊四边形与三角形面积关系求解;
解:∵△ABC与△FEC关于点C成中心对称,
∴点A,C,F共线,点B,C,E共线,AC=FC,BC=EC.
∴四边形ABFE是平行四边形.
∴S△ABC=S?ABFE=6.
(2)当∠ACB为多少度时,四边形ABFE为矩形?并说明理由.
【思路点拨】用逆向思维法探求条件.
解:当∠ACB=60°时,四边形ABFE是矩形.理由如下:
∵AC=AB,∠ACB=60°,∴△ABC是等边三角形.
∴AC=BC.
又∵AC=CF=AF,BC=EC=BE,∴AF=BE.
又∵四边形ABFE是平行四边形,∴?ABFE是矩形.
21.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,-1),B(-1,-4),C(-3,-4).
(1)作出△A1B1C1,使△A1B1C1与△ABC关于y轴成轴对称图形;
(2)作出与△ABC关于原点成中心对称的图形△A2B2C2,并求出△A2B2C2的面积.
解:(1)图略.
(2)图略,S△A2B2C2=12×3×2=3.
22.课外兴趣小组活动时,老师提出了如下问题:
如图1,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形的三边关系可得2感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
解决问题:受到上述的启发,请你证明下列命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
(1)求证:BE+CF>EF;
(2)若∠A=90°,探索线段BE,CF,EF之间的等量关系,并加以证明.
解:(1)延长FD到点G,使得DG=DF,连接BG,EG(或把△CFD绕点D逆时针旋转180°得到△BGD),
∴CF=BG,DF=DG.
又∵DE⊥DF,∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
(2)若∠A=90°,则∠EBC+∠FCB=90°.
由(1)知∠FCB=∠DBG,EF=EG,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,BE2+BG2=EG2,
∴BE2+CF2=EF2.
一、选择题
1.下列四组图形中,左边的图形与右边的图形成中心对称的有 ( )
A.1组 B.2组 C.3组 D.4组
2.若线段AB与线段CD(与AB不在同一条直线上)关于点O成中心对称,则AB和CD的关系是( )
A.AB=CD B.AB∥CD
C.AB平行且等于CD D.不确定
3.如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是 ( )
A.A与A'是对称点 B.BO=B'O
C.AB∥A'B' D.∠ACB=∠C'A'B'
4.如图,在?ABCD中,对角线AC,BD相交于点O,则图中成中心对称的三角形共有 ( )
A.4对 B.3对 C.2对 D.1对
5.如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是 ( )
A.1或4 B.2或3
C.3或4 D.1或2
6.如图,△ABC与△A'B'C'关于点O成中心对称,ED是△ABC的中位线,E'D'是△A'B'C'的中位线.已知BC=6,则E'D'=( )
A.1 B.3 C.4 D.6
7.如图,E,F分别是正方形ABCD的边CD,AD上的点,AF=ED,AE,BF相交于点O.下列结论:①AE=BF;②∠ABO=∠FAO;③△ABF与△DAE成中心对称.其中正确的结论有( )
A.0个 B.1个 C.2个 D.3个
8.如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,点F,下列结论:①点E和点F,点B和点D关于点O成中心对称;②直线BD必经过点O;③四边形DEOC与四边形BFOA的面积必相等;④△AOE与△COF成中心对称.其中正确结论的个数为 ( )
A.1 B.2 C.3 D.4
9.(2020·绍兴)如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
10.(2019·河南)如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为( )
A.(10,3) B.(-3,10)
C.(10,-3) D.(3,-10)
11.(2019·舟山)如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA′B′C′,再作图形OA′B′C′关于点O的中心对称图形OA″B″C″,则点C的对应点C″的坐标是( )
A.(2,-1) B.(1,-2)
C.(-2,1) D.(-2,-1)
二、填空题
12.如图,四边形ABCD与四边形FGHE关于图中的一个点成中心对称,则这个点是 .?
13.如图,AB=3,AC=1,∠D=90°,△DEC与△ABC关于点C成中心对称,则AE的长是 .?
14.如图,在四边形ABCD中,AD∥BC,AB=CD,且AD=12BC=2,E是BC的中点,则△ABE可以看成是由△DEC向左平移得到,平移的距离为 ;而△AED与△CDE是成中心对称的两个三角形,它们的对称中心是 .?
三、解答题
15.如图,在四边形ABCD中,AD∥BC,E是CD的中点.
(1)画图:连接AE并延长,交BC的延长线于点F,连接BE;
3700780364490(2)填空:点A与点F关于点 成中心对称,若AB=AD+BC,则△ABF是 三角形,此时点A与点F关于直线 成轴对称;?
(3)图中△ 的面积等于四边形ABCD的面积.?
16.由16个边长相等的小正方形组成的图形如图所示,请你用一条割线(可以是折线)将它分割成两个图形,使之关于某一点成中心对称,要求给出两种不同的方法.
17.如图,△ABC和△A'B'C'关于某一点成中心对称,某同学不小心把墨水泼在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
18.如图,AD是△ABC的边BC上的中线.
(1)画出以点D为对称中心,与△ABD成中心对称的三角形;
(2)若AB=10,AC=12,求AD长的取值范围.
19.(中考·枣庄)如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图①中,画出一个与△ABC成中心对称的格点三角形;
(2)在图②中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;
(3)在图③中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.
20.如图,在△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF.
(1)若四边形ABFE的面积为24,求△ABC的面积.
(2)当∠ACB为多少度时,四边形ABFE为矩形?并说明理由.
21.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,-1),B(-1,-4),C(-3,-4).
(1)作出△A1B1C1,使△A1B1C1与△ABC关于y轴成轴对称图形;
(2)作出与△ABC关于原点成中心对称的图形△A2B2C2,并求出△A2B2C2的面积.
22.课外兴趣小组活动时,老师提出了如下问题:
如图1,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形的三边关系可得2
解决问题:受到上述的启发,请你证明下列命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
(1)求证:BE+CF>EF;
(2)若∠A=90°,探索线段BE,CF,EF之间的等量关系,并加以证明.
参考答案
一、选择题
1.下列四组图形中,左边的图形与右边的图形成中心对称的有 (C)
A.1组 B.2组 C.3组 D.4组
2.若线段AB与线段CD(与AB不在同一条直线上)关于点O成中心对称,则AB和CD的关系是(C)
A.AB=CD B.AB∥CD
C.AB平行且等于CD D.不确定
3.如图,△ABC与△A'B'C'关于点O成中心对称,则下列结论不成立的是 (D)
A.A与A'是对称点 B.BO=B'O
C.AB∥A'B' D.∠ACB=∠C'A'B'
4.如图,在?ABCD中,对角线AC,BD相交于点O,则图中成中心对称的三角形共有 (A)
A.4对 B.3对 C.2对 D.1对
5.如图是由三个边长分别是2,3和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是 (D)
A.1或4 B.2或3
C.3或4 D.1或2
6.如图,△ABC与△A'B'C'关于点O成中心对称,ED是△ABC的中位线,E'D'是△A'B'C'的中位线.已知BC=6,则E'D'=( B )
A.1 B.3 C.4 D.6
7.如图,E,F分别是正方形ABCD的边CD,AD上的点,AF=ED,AE,BF相交于点O.下列结论:①AE=BF;②∠ABO=∠FAO;③△ABF与△DAE成中心对称.其中正确的结论有( C )
A.0个 B.1个 C.2个 D.3个
8.如图,已知△ABC与△CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,点F,下列结论:①点E和点F,点B和点D关于点O成中心对称;②直线BD必经过点O;③四边形DEOC与四边形BFOA的面积必相等;④△AOE与△COF成中心对称.其中正确结论的个数为 (D)
A.1 B.2 C.3 D.4
9.(2020·绍兴)如图,点O为矩形ABCD的对称中心,点E从点A出发沿AB向点B运动,移动到点B停止,延长EO交CD于点F,则四边形AECF形状的变化依次为( B )
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→菱形→正方形→矩形
10.(2019·河南)如图,在△OAB中,顶点O(0,0),A(-3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,则第70次旋转结束时,点D的坐标为( )
A.(10,3) B.(-3,10)
C.(10,-3) D.(3,-10)
【点拨】∵A(-3,4),B(3,4),∴AB=3+3=6.
∵四边形ABCD为正方形,∴AD=AB=6.
∴D(-3,10).
∵每4次一个循环,70=4×17+2,
∴第70次旋转结束时,相当于将△OAB与正方形ABCD组成的图形绕点O顺时针旋转2次,每次旋转90°.
∴所求点D的坐标为(3,-10).
【答案】D
11.(2019·舟山)如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA′B′C′,再作图形OA′B′C′关于点O的中心对称图形OA″B″C″,则点C的对应点C″的坐标是( A )
A.(2,-1) B.(1,-2)
C.(-2,1) D.(-2,-1)
二、填空题
12.如图,四边形ABCD与四边形FGHE关于图中的一个点成中心对称,则这个点是 O1 .?
13.如图,AB=3,AC=1,∠D=90°,△DEC与△ABC关于点C成中心对称,则AE的长是?13 .?
14.如图,在四边形ABCD中,AD∥BC,AB=CD,且AD=12BC=2,E是BC的中点,则△ABE可以看成是由△DEC向左平移得到,平移的距离为 2 ;而△AED与△CDE是成中心对称的两个三角形,它们的对称中心是 DE的中点 .?
三、解答题
15.如图,在四边形ABCD中,AD∥BC,E是CD的中点.
(1)画图:连接AE并延长,交BC的延长线于点F,连接BE;
(2)填空:点A与点F关于点 E 成中心对称,若AB=AD+BC,则△ABF是 等腰 三角形,此时点A与点F关于直线 BE 成轴对称;?
(3)图中△ ABF 的面积等于四边形ABCD的面积.?
解:(1)图略.
16.由16个边长相等的小正方形组成的图形如图所示,请你用一条割线(可以是折线)将它分割成两个图形,使之关于某一点成中心对称,要求给出两种不同的方法.
解:如图所示.(答案不唯一)
17.如图,△ABC和△A'B'C'关于某一点成中心对称,某同学不小心把墨水泼在纸上,只能看到△ABC和线段BC的对应线段B'C',请你帮该同学找到对称中心O,且补全△A'B'C'.
解:如图所示,BB',CC'的交点即为O,△A'B'C'即为所求.
18.如图,AD是△ABC的边BC上的中线.
(1)画出以点D为对称中心,与△ABD成中心对称的三角形;
解:延长AD至E,使DE=AD,
连接CE,则△ECD即为所求,如图所示.
(2)若AB=10,AC=12,求AD长的取值范围.
解:由(1)知AD=DE,EC=AB=10.
在△ACE中,由AC-EC
∴1
(1)在图①中,画出一个与△ABC成中心对称的格点三角形;
解:如图①,△DEC为所求作的三角形.(答案不唯一)
(2)在图②中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;
解:如图②,△ADC为所求作的三角形.
(答案不唯一)
(3)在图③中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形.
如图③,△DEC为所求作的三角形.
20.如图,在△ABC中,AB=AC,△ABC与△FEC关于点C成中心对称,连接AE,BF.
(1)若四边形ABFE的面积为24,求△ABC的面积.
【思路点拨】利用特殊四边形与三角形面积关系求解;
解:∵△ABC与△FEC关于点C成中心对称,
∴点A,C,F共线,点B,C,E共线,AC=FC,BC=EC.
∴四边形ABFE是平行四边形.
∴S△ABC=S?ABFE=6.
(2)当∠ACB为多少度时,四边形ABFE为矩形?并说明理由.
【思路点拨】用逆向思维法探求条件.
解:当∠ACB=60°时,四边形ABFE是矩形.理由如下:
∵AC=AB,∠ACB=60°,∴△ABC是等边三角形.
∴AC=BC.
又∵AC=CF=AF,BC=EC=BE,∴AF=BE.
又∵四边形ABFE是平行四边形,∴?ABFE是矩形.
21.如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,-1),B(-1,-4),C(-3,-4).
(1)作出△A1B1C1,使△A1B1C1与△ABC关于y轴成轴对称图形;
(2)作出与△ABC关于原点成中心对称的图形△A2B2C2,并求出△A2B2C2的面积.
解:(1)图略.
(2)图略,S△A2B2C2=12×3×2=3.
22.课外兴趣小组活动时,老师提出了如下问题:
如图1,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形的三边关系可得2
解决问题:受到上述的启发,请你证明下列命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
(1)求证:BE+CF>EF;
(2)若∠A=90°,探索线段BE,CF,EF之间的等量关系,并加以证明.
解:(1)延长FD到点G,使得DG=DF,连接BG,EG(或把△CFD绕点D逆时针旋转180°得到△BGD),
∴CF=BG,DF=DG.
又∵DE⊥DF,∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
(2)若∠A=90°,则∠EBC+∠FCB=90°.
由(1)知∠FCB=∠DBG,EF=EG,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,BE2+BG2=EG2,
∴BE2+CF2=EF2.
同课章节目录
