2021年春重庆市长寿区双龙镇中学八年级数学下6月月考试题(word版含答案)
文档属性
| 名称 | 2021年春重庆市长寿区双龙镇中学八年级数学下6月月考试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 369.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 21:20:51 | ||
图片预览




文档简介
2021年春八年级数学下6月月考试题
(考试总分:150
分)
一、
单选题
(本题共计12小题,总分48分)
1.(4分)函数、自变量的取值范围是(
)
A.
B.
C.
D.
2.(4分)已知的三边分别是6,8,
10,则的面积是(
)
A.24
B.30
C.40
D.48
3.(4分)下列式子中,属于最简二次根式的是(
)
A.
B.
C.
D.
4.(4分)若点在正比例函数的图象上,则这个正比例函数的解析式是(
)
A.
B.
C.
D.
5.(4分)甲、乙两组数据的平均数相等,甲组数据的方差,乙组数据的方差0.055,则(
)
A.甲组数据比乙组数据波动大
B.乙组数据比甲组数据波动大
C.甲组数据与乙组数据的波动一样大
D.甲,乙两组数据的数据波动不能比较
6.(4分)如图,菱形中,点分别是的中点,若,则菱形的周长是(
)
A.12
B.16
C.20
D.24
7.(4分)若数据2、4、
、9、8的平均数是5,则这组数据的中位数是(
)
A.2
B.4
C.8
D.9
8.(4分)关于的一次函数的图象可能正确的是(
)
A.
B.
C.
D.
9.(4分)等式成立的条件是(
)
A.
B.
C.
D.或
10.(4分)如图,圆柱形开口杯底部固定在长方体水池底,向水池匀速注入水(倒在杯外),水池中水面高度为,注水时间为,则与之间的关系大致为下图中的(
)
A.
B.
C.
D.
11.(4分)在学习“勾股数”的知识时,爱动脑的小明发现了一组有规律的勾股数,并将它们记录在如下的表格中,则当时,的值为(
)
A.250
B.288
C.300
D.574
12.(4分)若实数使得关于的分式方程的解为负数,且使得关于的一次函数过第一、二、三象限,则符合条件的所有整数的和为(
)
A.6
B.5
C.3
D.2
二、
填空题
(本题共计6小题,总分24分)
13.(4分)计算:=__________.
14.(4分)在一次函数中,若随着的增大而减小,则的取值范围是__________.
15.(4分)如图,在矩形中,对角线与相交于点,过点作,垂足为点,若,则_____.
16.(4分)疫情期间,张老师为了了解本班学生居家学习期间每天体育锻炼的情况,张老师随机抽查了本班20名学生,统计数据如下表:
若这20名学生每天体育锻炼时间的平均数为小时,则的值为_____.
17.(4分)武汉疫情爆发期间,大学生小玲和小丽应聘成为了阳光小区的疫情防控志愿者,一天,小玲从阳光小区出发骑三轮车匀速到距离7500米处的区疾病防控中心领取防疫物资,出发一段时间后,小丽发现小玲忘记带了社区介绍信,立即骑自行车沿小玲行驶的路线匀速行驶去追赶,当小丽追上小玲后,立即将介绍信交给了她,并用2分钟时间与小玲核对了一下防疫物资的清,单,然后小玲继续以原速度前往区疾病防控中心,而小丽则按原路以原来速度的一半匀速返回阳光小区,设小丽与小玲之间的距离y(米)与小玲从阳光小区出发后的时间x(分)之间的关系如图所示,当小丽刚好返回到阳光小区时,小玲离区疾病防控中心的距离还有_____米?
18.(4分)如图所示,直线与两坐标轴分别交于、两点,点C是的中点,、分别是直线轴上的动点,则周长的最小值是_____.
三、
解答题
(本题共计8小题,总分78分)
19.(10分)计算:
(1);
(2).
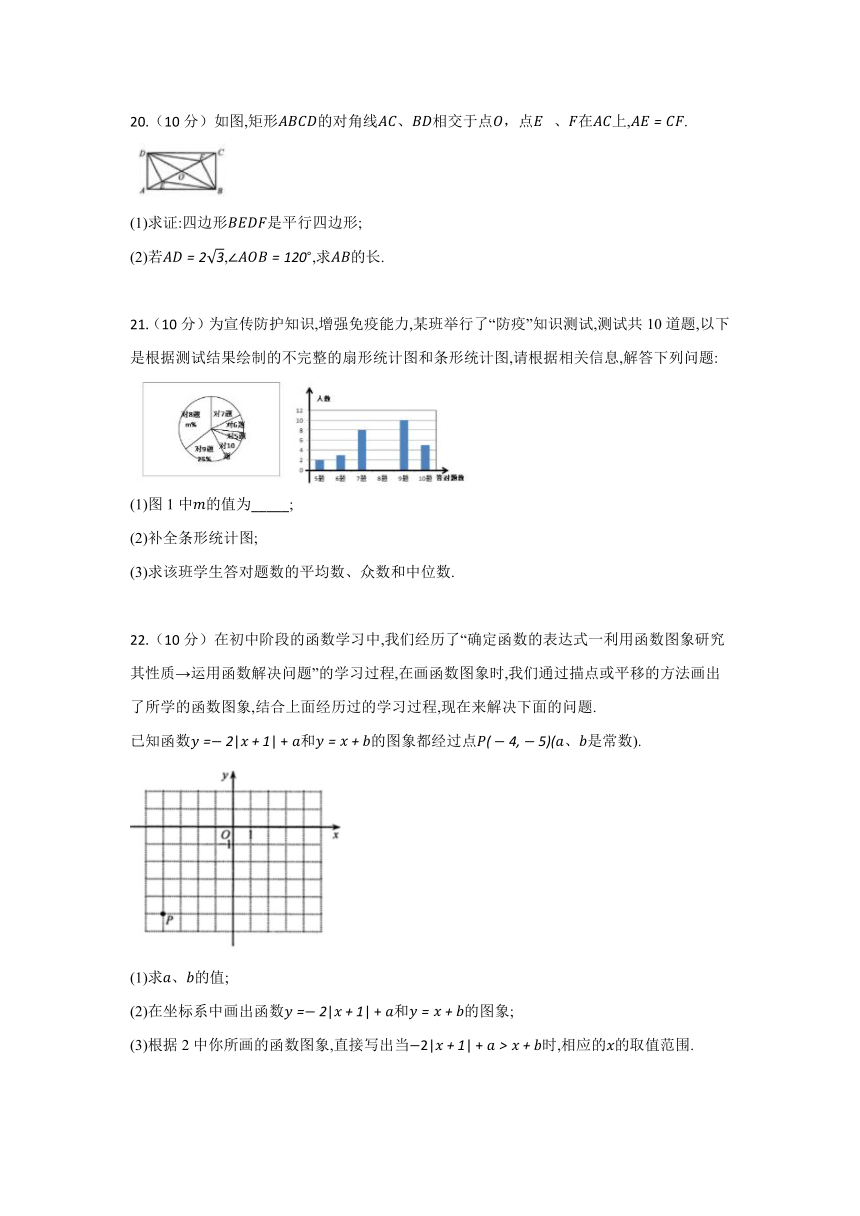
20.(10分)如图,矩形的对角线、相交于点,点、在上,.
(1)求证:四边形是平行四边形;
(2)若,,求的长.
21.(10分)为宣传防护知识,增强免疫能力,某班举行了“防疫”知识测试,测试共10道题,以下是根据测试结果绘制的不完整的扇形统计图和条形统计图,请根据相关信息,解答下列问题:
(1)图1中的值为_____;
(2)补全条形统计图;
(3)求该班学生答对题数的平均数、众数和中位数.
22.(10分)在初中阶段的函数学习中,我们经历了“确定函数的表达式一利用函数图象研究其性质→运用函数解决问题”的学习过程,在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象,结合上面经历过的学习过程,现在来解决下面的问题.
已知函数和的图象都经过点、是常数).
(1)求、的值;
(2)在坐标系中画出函数和的图象;
(3)根据2中你所画的函数图象,直接写出当时,相应的的取值范围.
23.(10分)阅读下列两则材料,回答问题.
材料一:定义直线与直线互为“共同体直线”,例如,直线与直线互为“共同体直线”
材料二:对于半面直角坐标系中的任意两点,,之两点间的直角距离,例如:、两点间的直角距离为,改为一个定点,是直线上的动点,我们把的最小值叫做到直线的直角距离.
(1)计算两点间的直角距离_____,直线上的一点又是它的“共同体直线”上的点,求点的坐标.
(2)对于直线上的任意一点,都有点在它的“共同体直线”上,试求点到直线的直角距离.
24.(10分)为支援武汉抗击新冠肺炎,某地捐赠了240吨的救援物资并联系了一家快递公司用甲、乙两种型号的货车进行运送,已知甲型货车3辆、乙型货车2辆时,需运费1300元;甲型货车1辆、乙型货车4辆时,需运费1100元.
(1)甲、乙两种型号的货车的运费每辆各是多少元?
(2)已知甲型货车每辆可装15吨物资,乙型货车每辆可装10吨物资,现快递公司计划安排甲型货车和乙型货车共20辆,一次性将救援物资全部运往武汉,设安排甲型货车辆车,那么总运费为元,求与之间的函数关系式,并求出的最小值.
25.(10分)已知:在平行四边形中,过点作,过点作的垂线,分别交于点、、,且.
(1)若,求的值;
(2)连接,证明:.
26.(8分)如图,在平面直角坐标系中,矩形的两条边分别在坐标轴上,.
(1)求所在的直线的解析式;
(2)把矩形沿直线对折,使点落在点处,与相交于点,求点的坐标;
(3)在直线上是否存在点,使以点三点为顶点的三角形是等腰三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
答案
一、
单选题
(本题共计12小题,总分48分)
1.(4分)【答案】C
2.(4分)【答案】A
3.(4分)【答案】D
4.(4分)【答案】B
5.(4分)【答案】B
6.(4分)【答案】D
7.(4分)【答案】B
8.(4分)【答案】C
9.(4分)【答案】A
10.(4分)【答案】B
11.(4分)【答案】B
12.(4分)【答案】D
二、
填空题
(本题共计6小题,总分24分)
13.(4分)【答案】
14.(4分)【答案】
15.(4分)【答案】
16.(4分)【答案】
1.3
17.(4分)【答案】625
18.(4分)【答案】
三、
解答题
(本题共计8小题,总分78分)
19.(10分)(1);
【解析】原式;
(2).
【解析】原式
.
20.(10分)(1)在矩形中,
∴,
∵,
∴,
∴四边形是平行四边形.
(2)由1可知:,
∵,
∴,
,
∴.
21.(10分)(1)∵
被调查的总人数为(人),
∴答对8题的人数为(人),
∴,即;
故答案为:.
(2)补全条形图如下:
(3)答对题数的平均数为.
22.(10分)(1)∵函数和的图象都经过点是常数),
,
∴;
(2)函数中,当时,,
当时,,图象经过,
函数中,当图象经过,
在坐标系中画出函数和的图象如图:
(3)由图象可知:当时,相应的的取值范围是.
23.(10分)(1)
【解析】∵、则两点的直角距离为,
∴、两点间的直角距离,
直线的“共同体直线”是,
由题意知是它们的交点,则有:
,
解得,
∴点的坐标为:.
(2)10.
【解析】∵点是直线上的任意一点,
∴
∵点是直线的“共同体直线”上的一点,
即在直线上,
∴
,
将①代入②得,,
整理得:,
∴,
∵对于任意一点等式均成立,
∴,
解得,
,
∵是直线上的动点,定点,
∴,
∴,
∵当时,代数有最小值10,
∴点到直线的直角距离是10.
24.(10分)(1)设每辆甲型货车的运费为元,每辆乙型货车的运费为元,根据题意得:
,
解得.
答:每辆甲型货车的运费为300元,每辆乙型货车的运费为200元;
(2)设安排甲型货车辆车,那么安排乙型货车辆车,根据题意得:
,
由题意得:,
解得,
又,
∴随的增大而增大,
∴时,最小,最小值为4800元.
25.(10分)(1)∵四边形是平行四边形,
∴,,
∵,
∴,
∴,
∴,,
,
在中,,
∴,
∴,
.
(2)证明:过点作,交延长线于,如图所示:
∵,
∴,
∵
∴,
∴,
∴,
∵,
,
在中,
∴,
,
∵,
,
∵,
∴,
在中,,
∴,
∴
∴是等腰直角三角形,
∴,
∴,
∴.
26.(8分)(1)设直线的解析式是,
∵,
∴,,
∵点都在直线上,
∴,
解得:,
∴直线的解析式为;
(2)连接,由折叠可知,
设,则,
∵在中,,
∴,
解得:,
∴点的坐标为,
(3)存在,
,
∴,
∵点在直线上,
∴设,
①当时,点是线段,的中垂线与直线的交点,则;
②当时,,
整理得:,
解得:,
,;
③当时,
整理得:,
则,
∵,
,
,
综上所述,符合条件的点P有:
,,,.
(考试总分:150
分)
一、
单选题
(本题共计12小题,总分48分)
1.(4分)函数、自变量的取值范围是(
)
A.
B.
C.
D.
2.(4分)已知的三边分别是6,8,
10,则的面积是(
)
A.24
B.30
C.40
D.48
3.(4分)下列式子中,属于最简二次根式的是(
)
A.
B.
C.
D.
4.(4分)若点在正比例函数的图象上,则这个正比例函数的解析式是(
)
A.
B.
C.
D.
5.(4分)甲、乙两组数据的平均数相等,甲组数据的方差,乙组数据的方差0.055,则(
)
A.甲组数据比乙组数据波动大
B.乙组数据比甲组数据波动大
C.甲组数据与乙组数据的波动一样大
D.甲,乙两组数据的数据波动不能比较
6.(4分)如图,菱形中,点分别是的中点,若,则菱形的周长是(
)
A.12
B.16
C.20
D.24
7.(4分)若数据2、4、
、9、8的平均数是5,则这组数据的中位数是(
)
A.2
B.4
C.8
D.9
8.(4分)关于的一次函数的图象可能正确的是(
)
A.
B.
C.
D.
9.(4分)等式成立的条件是(
)
A.
B.
C.
D.或
10.(4分)如图,圆柱形开口杯底部固定在长方体水池底,向水池匀速注入水(倒在杯外),水池中水面高度为,注水时间为,则与之间的关系大致为下图中的(
)
A.
B.
C.
D.
11.(4分)在学习“勾股数”的知识时,爱动脑的小明发现了一组有规律的勾股数,并将它们记录在如下的表格中,则当时,的值为(
)
A.250
B.288
C.300
D.574
12.(4分)若实数使得关于的分式方程的解为负数,且使得关于的一次函数过第一、二、三象限,则符合条件的所有整数的和为(
)
A.6
B.5
C.3
D.2
二、
填空题
(本题共计6小题,总分24分)
13.(4分)计算:=__________.
14.(4分)在一次函数中,若随着的增大而减小,则的取值范围是__________.
15.(4分)如图,在矩形中,对角线与相交于点,过点作,垂足为点,若,则_____.
16.(4分)疫情期间,张老师为了了解本班学生居家学习期间每天体育锻炼的情况,张老师随机抽查了本班20名学生,统计数据如下表:
若这20名学生每天体育锻炼时间的平均数为小时,则的值为_____.
17.(4分)武汉疫情爆发期间,大学生小玲和小丽应聘成为了阳光小区的疫情防控志愿者,一天,小玲从阳光小区出发骑三轮车匀速到距离7500米处的区疾病防控中心领取防疫物资,出发一段时间后,小丽发现小玲忘记带了社区介绍信,立即骑自行车沿小玲行驶的路线匀速行驶去追赶,当小丽追上小玲后,立即将介绍信交给了她,并用2分钟时间与小玲核对了一下防疫物资的清,单,然后小玲继续以原速度前往区疾病防控中心,而小丽则按原路以原来速度的一半匀速返回阳光小区,设小丽与小玲之间的距离y(米)与小玲从阳光小区出发后的时间x(分)之间的关系如图所示,当小丽刚好返回到阳光小区时,小玲离区疾病防控中心的距离还有_____米?
18.(4分)如图所示,直线与两坐标轴分别交于、两点,点C是的中点,、分别是直线轴上的动点,则周长的最小值是_____.
三、
解答题
(本题共计8小题,总分78分)
19.(10分)计算:
(1);
(2).
20.(10分)如图,矩形的对角线、相交于点,点、在上,.
(1)求证:四边形是平行四边形;
(2)若,,求的长.
21.(10分)为宣传防护知识,增强免疫能力,某班举行了“防疫”知识测试,测试共10道题,以下是根据测试结果绘制的不完整的扇形统计图和条形统计图,请根据相关信息,解答下列问题:
(1)图1中的值为_____;
(2)补全条形统计图;
(3)求该班学生答对题数的平均数、众数和中位数.
22.(10分)在初中阶段的函数学习中,我们经历了“确定函数的表达式一利用函数图象研究其性质→运用函数解决问题”的学习过程,在画函数图象时,我们通过描点或平移的方法画出了所学的函数图象,结合上面经历过的学习过程,现在来解决下面的问题.
已知函数和的图象都经过点、是常数).
(1)求、的值;
(2)在坐标系中画出函数和的图象;
(3)根据2中你所画的函数图象,直接写出当时,相应的的取值范围.
23.(10分)阅读下列两则材料,回答问题.
材料一:定义直线与直线互为“共同体直线”,例如,直线与直线互为“共同体直线”
材料二:对于半面直角坐标系中的任意两点,,之两点间的直角距离,例如:、两点间的直角距离为,改为一个定点,是直线上的动点,我们把的最小值叫做到直线的直角距离.
(1)计算两点间的直角距离_____,直线上的一点又是它的“共同体直线”上的点,求点的坐标.
(2)对于直线上的任意一点,都有点在它的“共同体直线”上,试求点到直线的直角距离.
24.(10分)为支援武汉抗击新冠肺炎,某地捐赠了240吨的救援物资并联系了一家快递公司用甲、乙两种型号的货车进行运送,已知甲型货车3辆、乙型货车2辆时,需运费1300元;甲型货车1辆、乙型货车4辆时,需运费1100元.
(1)甲、乙两种型号的货车的运费每辆各是多少元?
(2)已知甲型货车每辆可装15吨物资,乙型货车每辆可装10吨物资,现快递公司计划安排甲型货车和乙型货车共20辆,一次性将救援物资全部运往武汉,设安排甲型货车辆车,那么总运费为元,求与之间的函数关系式,并求出的最小值.
25.(10分)已知:在平行四边形中,过点作,过点作的垂线,分别交于点、、,且.
(1)若,求的值;
(2)连接,证明:.
26.(8分)如图,在平面直角坐标系中,矩形的两条边分别在坐标轴上,.
(1)求所在的直线的解析式;
(2)把矩形沿直线对折,使点落在点处,与相交于点,求点的坐标;
(3)在直线上是否存在点,使以点三点为顶点的三角形是等腰三角形?若存在,请直接写出点的坐标;若不存在,请说明理由.
答案
一、
单选题
(本题共计12小题,总分48分)
1.(4分)【答案】C
2.(4分)【答案】A
3.(4分)【答案】D
4.(4分)【答案】B
5.(4分)【答案】B
6.(4分)【答案】D
7.(4分)【答案】B
8.(4分)【答案】C
9.(4分)【答案】A
10.(4分)【答案】B
11.(4分)【答案】B
12.(4分)【答案】D
二、
填空题
(本题共计6小题,总分24分)
13.(4分)【答案】
14.(4分)【答案】
15.(4分)【答案】
16.(4分)【答案】
1.3
17.(4分)【答案】625
18.(4分)【答案】
三、
解答题
(本题共计8小题,总分78分)
19.(10分)(1);
【解析】原式;
(2).
【解析】原式
.
20.(10分)(1)在矩形中,
∴,
∵,
∴,
∴四边形是平行四边形.
(2)由1可知:,
∵,
∴,
,
∴.
21.(10分)(1)∵
被调查的总人数为(人),
∴答对8题的人数为(人),
∴,即;
故答案为:.
(2)补全条形图如下:
(3)答对题数的平均数为.
22.(10分)(1)∵函数和的图象都经过点是常数),
,
∴;
(2)函数中,当时,,
当时,,图象经过,
函数中,当图象经过,
在坐标系中画出函数和的图象如图:
(3)由图象可知:当时,相应的的取值范围是.
23.(10分)(1)
【解析】∵、则两点的直角距离为,
∴、两点间的直角距离,
直线的“共同体直线”是,
由题意知是它们的交点,则有:
,
解得,
∴点的坐标为:.
(2)10.
【解析】∵点是直线上的任意一点,
∴
∵点是直线的“共同体直线”上的一点,
即在直线上,
∴
,
将①代入②得,,
整理得:,
∴,
∵对于任意一点等式均成立,
∴,
解得,
,
∵是直线上的动点,定点,
∴,
∴,
∵当时,代数有最小值10,
∴点到直线的直角距离是10.
24.(10分)(1)设每辆甲型货车的运费为元,每辆乙型货车的运费为元,根据题意得:
,
解得.
答:每辆甲型货车的运费为300元,每辆乙型货车的运费为200元;
(2)设安排甲型货车辆车,那么安排乙型货车辆车,根据题意得:
,
由题意得:,
解得,
又,
∴随的增大而增大,
∴时,最小,最小值为4800元.
25.(10分)(1)∵四边形是平行四边形,
∴,,
∵,
∴,
∴,
∴,,
,
在中,,
∴,
∴,
.
(2)证明:过点作,交延长线于,如图所示:
∵,
∴,
∵
∴,
∴,
∴,
∵,
,
在中,
∴,
,
∵,
,
∵,
∴,
在中,,
∴,
∴
∴是等腰直角三角形,
∴,
∴,
∴.
26.(8分)(1)设直线的解析式是,
∵,
∴,,
∵点都在直线上,
∴,
解得:,
∴直线的解析式为;
(2)连接,由折叠可知,
设,则,
∵在中,,
∴,
解得:,
∴点的坐标为,
(3)存在,
,
∴,
∵点在直线上,
∴设,
①当时,点是线段,的中垂线与直线的交点,则;
②当时,,
整理得:,
解得:,
,;
③当时,
整理得:,
则,
∵,
,
,
综上所述,符合条件的点P有:
,,,.
同课章节目录
