2021-2022学年湘教新版八年级上册数学《第2章 三角形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年湘教新版八年级上册数学《第2章 三角形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 289.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 21:26:47 | ||
图片预览



文档简介
2021-2022学年湘教新版八年级上册数学《第2章
三角形》单元测试卷
一.选择题
1.如图所示,以BC为边的三角形共有( )
A.1个
B.2个
C.3个
D.4个
2.如图中,三角形的个数为( )
A.3个
B.4个
C.5个
D.6个
3.已知三角形ABC三边a、b、c满足(a﹣b)2+|b﹣c|=0,则△ABC的形状是( )
A.钝角三角形
B.直角三角形
C.等边三角形
D.以上都不对
4.画△ABC中AC边上的高,下列四个画法中正确的是( )
A.
B.
C.
D.
5.三角形的重心是( )
A.三角形三条边上中线的交点
B.三角形三条边上高线的交点
C.三角形三条边垂直平分线的交点
D.三角形三条内角平分线的交点
6.下列长度的三条线段能构成三角形的是( )
A.3,4,8
B.3,4,7
C.5,6,10
D.5,6,11
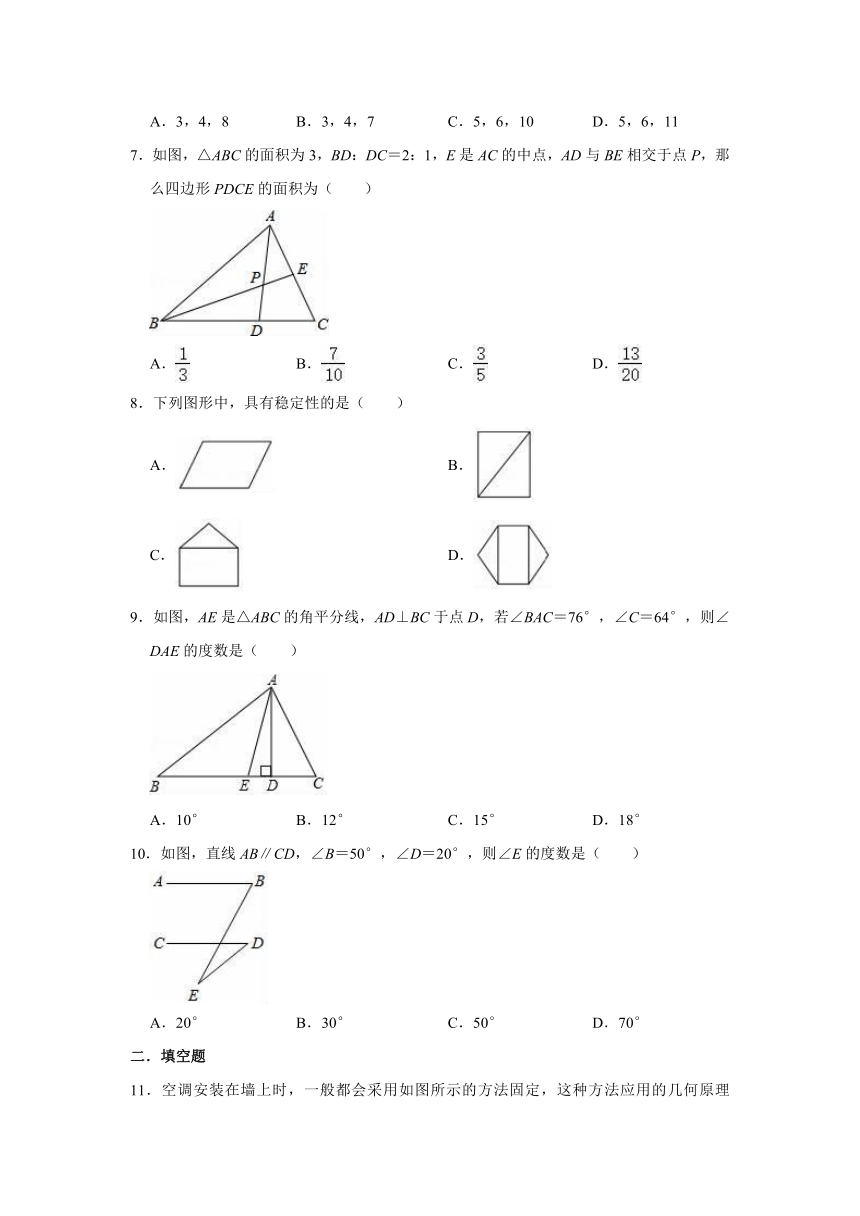
7.如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为( )
A.
B.
C.
D.
8.下列图形中,具有稳定性的是( )
A.
B.
C.
D.
9.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=76°,∠C=64°,则∠DAE的度数是( )
A.10°
B.12°
C.15°
D.18°
10.如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是( )
A.20°
B.30°
C.50°
D.70°
二.填空题
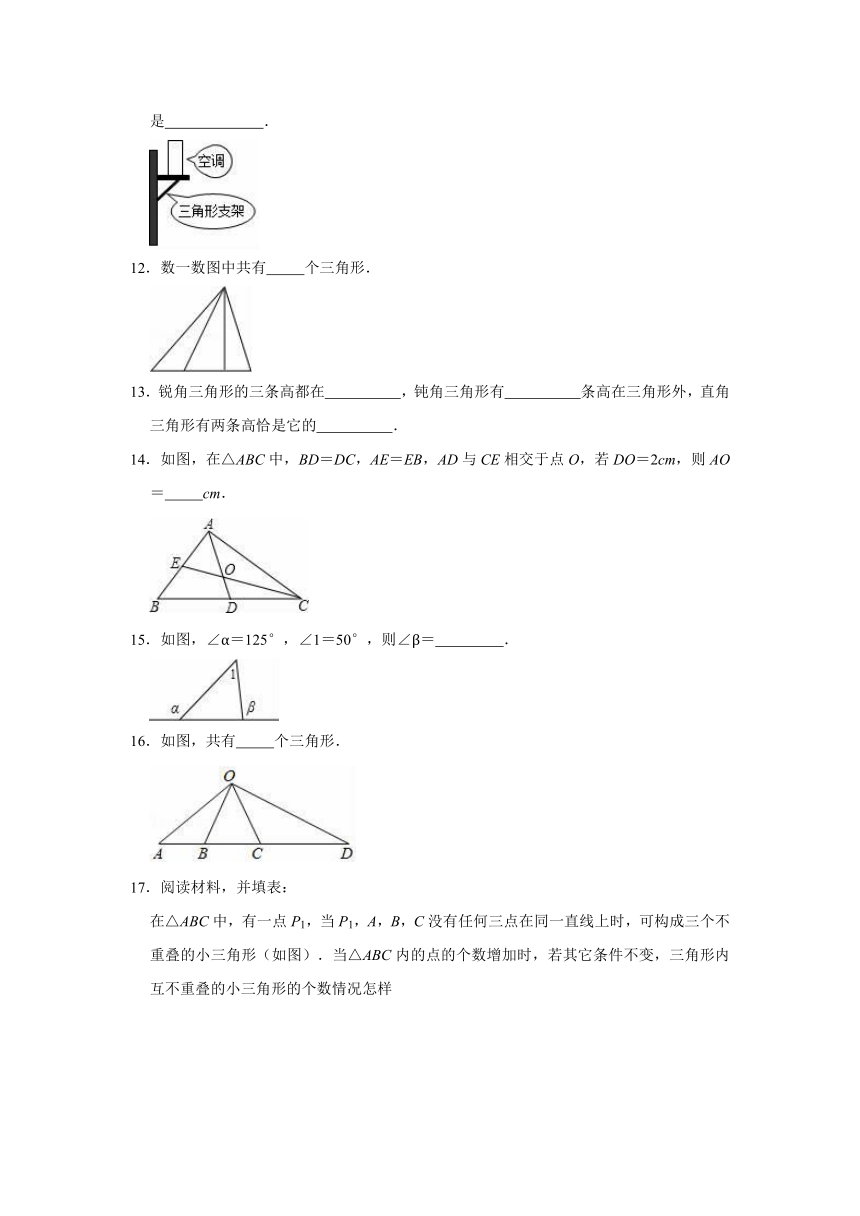
11.空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是
.
12.数一数图中共有
个三角形.
13.锐角三角形的三条高都在
,钝角三角形有
条高在三角形外,直角三角形有两条高恰是它的
.
14.如图,在△ABC中,BD=DC,AE=EB,AD与CE相交于点O,若DO=2cm,则AO=
cm.
15.如图,∠α=125°,∠1=50°,则∠β=
.
16.如图,共有
个三角形.
17.阅读材料,并填表:
在△ABC中,有一点P1,当P1,A,B,C没有任何三点在同一直线上时,可构成三个不重叠的小三角形(如图).当△ABC内的点的个数增加时,若其它条件不变,三角形内互不重叠的小三角形的个数情况怎样
完成下表:
ABC内点的个数
1
2
3
…
1002
构成不重叠的小三角形的个数
3
5
…
按表格顺序填入为
,
.
18.已知D、E分别是△ABC的边BC和AC的中点,若△ABC的面积=24cm2,则△DEC的面积为
.
19.设△ABC三边为a、b、c,其中a、b满足|a+b﹣6|+(a﹣b+4)2=0,则第三边c的取值范围
.
20.如图,在直角三角形ABC中,点P、Q分别是AC、BC边上的两个动点,MP、NQ分别平分∠APQ和∠BQP,交AB于点M、N,MR、NR又分别平分∠BMP和∠ANQ,两条角平分线交于点R,则∠R=
°.
三.解答题
21.(1)下列图形中具有稳定性是
;(只填图形序号)
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
22.【数学经验】三角形的中线的性质:三角形的中线等分三角形的面积.
【经验发展】面积比和线段比的联系:
(1)如图1,M为△ABC的AB上一点,且BM=2AM,若△ABC的面积为a,若△CBM的面积为S,则S=
(用含a的代数式表示).
【结论应用】如图2,已知△CDE的面积为1,,,求△ABC的面积.
【迁移应用】如图3,在△ABC中,M是AB的三等分点(AM=AB),N是BC的中点,若△ABC的面积是1,请直接写出四边形BMDN的面积为
.
23.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
24.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为
个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
25.观察以下图形,回答问题:
(1)图②有
个三角形;图③有
个三角形;图④有
个三角形;…猜测第七个图形中共有
个三角形.
(2)按上面的方法继续下去,第n个图形中有
个三角形(用含n的代数式表示结论).
26.已知AD是△ABC的高,∠BAD=70°,∠CAD=20°,求∠BAC的度数.
27.如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O.
(1)BO与OD的长度有什么关系?并证明你的结论.
(2)BC边上的中线是否一定过点O?为什么?
参考答案与试题解析
一.选择题
1.解:以BC为边的三角形有△BCE,△BAC,△DBC,
故选:C.
2.解:根据图示知,图中的三角形有:△ABE,△ABC,△DEC,△DBC,△EBC,共有5个.
故选:C.
3.解:根据非负数的性质,a﹣b=0,b﹣c=0,
解得a=b,b=c,
所以,a=b=c,
所以,△ABC是等边三角形.
故选:C.
4.解:由三角形的高线的定义,C选项图形表示△ABC中AC边上的高.
故选:C.
5.解:三角形的重心是三条中线的交点,
故选:A.
6.解:根据三角形任意两边的和大于第三边,得
A中,3+4=7<8,不能组成三角形;
B中,3+4=7,不能组成三角形;
C中,5+6=11>10,能够组成三角形;
D中,5+6=11,不能组成三角形.
故选:C.
7.解:连接CP,
设△CPE的面积是x,△CDP的面积是y.
∵BD:DC=2:1,E为AC的中点,
∴△BDP的面积是2y,△APE的面积是x,
∵BD:DC=2:1,CE:AC=1:2,
∴△ABP的面积是4x.
∴4x+x=2y+x+y,
解得y=x.
又∵4x+x=,
x=.
则四边形PDCE的面积为x+y=.
故选:B.
8.解:根据三角形具有稳定性可得选项B具有稳定性,
故选:B.
9.解:∵AE平分∠BAC,
∴∠CAE=∠CAB=×76°=38°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=90°﹣64°=26°,
∴∠DAE=∠EAC﹣∠CAD=38°﹣26°=12°,
故选:B.
10.解:∵AB∥CD,
∴∠BMD=∠B=50°,
又∵∠BMD是△CDE的外角,
∴∠E=∠BMD﹣∠D=50°﹣20°=30°.
故选:B.
二.填空题
11.解:这种方法应用的数学知识是:三角形的稳定性,
故答案为:三角形具有稳定性.
12.解:线段AD上有4个点,
可以与E组成的三角形有×4×(4﹣1)=6个.
故答案是:6.
13.解:锐角三角形有三条高,高都在三角形内部,且锐角三角形三条高的交点一定在三角形内部;
钝角三角形有三条高,一条高在三角形内部,另外两条高在三角形外部,
直角三角形有两条高即三角形的两条直角边,一条在内部,三条高的交点在顶点上;
故答案分别是:三角形内部;二;直角边.
14.解:∵BD=DC,AE=EB,AD与CE相交于点O,
∴O是△ABC的重心,
∴AO=2DO=2×2=4cm.
故答案为:4.
15.解:∵∠2=∠α﹣∠1=75°,
∴∠β=180°﹣∠2=180°﹣75°=105°.
16.解:图中有:△OAB,△OAC,△OAD,△OBC,△OCD,△OBD,共6个.
故答案为:6.
17.解:当△ABC内的点的个数是n时,三角形内互不重叠的小三角形的个数2n+1.∴按表格顺序填入为7,2005.
18.解:∵D、E分别是△ABC的边BC和AC的中点,
∴S△ABC=2S△ADC
又∵D是△ABC的边BC的中点,S△ABC=24cm2,
∴S△DEC=S△ABC=6cm2.
故答案为:6cm2.
19.解:由题意得:,
解得,
根据三角形的三边关系定理可得5﹣1<c<5+1,
即4<c<6.
故答案为:4<c<6.
20.解:∵∠C+∠A+∠B=180°,∠C+∠CPQ+∠CQP=180°,∠C=90°,
∴∠A+∠B=90°,∠CPQ+∠CQP=90°,
∴∠APQ+∠BQP+∠CPQ+∠CQP=360°,
∴∠APQ+∠BQP=270°,
∵MP、NQ分别平分∠APQ和∠BQP,
∴∠MPQ+∠NQP=∠APM+∠BQN=135°,
∵∠MPQ+∠NQP+∠PMN+∠QNM=360°,
∴∠PMN+∠QNM=225°,
∵MR、NR又分别平分∠BMP和∠ANQ,
∴∠NMR+∠MNR=112.5°,
∵∠NMR+∠MNR+∠R=180°,
∴∠R=67.5°.
故答案为67.5.
三.解答题
21.解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
22.解:(1)∵M为△ABC的AB上一点,且BM=2AM,
∴S=a,
故答案为a;
(2)连接BD,
∵△CDE的面积为1,,
∴S△BDC=3S△DEC=3,
∵,
∴S△ABC=4S△BDC=12;
(3)连接BD,
设S△ADM=a,
∵M是AB的三等分点(AM=AB),
∴S△ABD=3a,S△BDM=2a,
∵N是BC的中点,
∴S△ABN=S△ACN,S△BDN=S△CDN,
∴S△ADC=S△ADB=3a,
∴S△ACM=4a,
∵AM=AB,
∴S△CBM=2S△ACM=8a,
∴S△CDB=6a,S△ABC=12a,
∴S△BDN=3a,
∴S四边形BMDN=5a,
∴S四边形BMDN=S△ABC=×1=,
故答案为.
23.解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
24.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
25.解:(1)图②有3个三角形;图③有5个三角形;图④有7个三角形;…猜测第七个图形中共有13个三角形.
(2)∵图②有3个三角形,3=2×2﹣1;
图③有5个三角形,5=2×3﹣1;
图④有7个三角形,7=2×4﹣1;
∴第n个图形中有(2n﹣1)个三角形.
故答案为3,5,7,13,(2n﹣1).
26.解:①如图1,当高AD在△ABC的内部时,
∠BAC=∠BAD+∠CAD=70°+20°=90°;
②如图2,当高AD在△ABC的外部时,
∠BAC=∠BAD﹣∠CAD=70°﹣20°=50°,
综上所述,∠BAC的度数为90°或50°.
27.解:(1)BO=2OD,理由如下:
连接DE,
∵BD、CE是边AC、AB上的中线,
∴DE∥BC,DE=BC.
∴△ODE~△OBC,
∴=,
即BO=2OD.
(2)BC边上的中线一定过点O,
理由是:作BC边上的中线AF,交BD于M,
连接DF,
∵BD、AF是边AC、BC上的中线,
.∴DF∥BA,DF=BA.
∴△MDF~△MBA
∴===,
即BD=3DM,
BO=BD,
∴O和M重合,
即BC边上的中线一定过点O.
三角形》单元测试卷
一.选择题
1.如图所示,以BC为边的三角形共有( )
A.1个
B.2个
C.3个
D.4个
2.如图中,三角形的个数为( )
A.3个
B.4个
C.5个
D.6个
3.已知三角形ABC三边a、b、c满足(a﹣b)2+|b﹣c|=0,则△ABC的形状是( )
A.钝角三角形
B.直角三角形
C.等边三角形
D.以上都不对
4.画△ABC中AC边上的高,下列四个画法中正确的是( )
A.
B.
C.
D.
5.三角形的重心是( )
A.三角形三条边上中线的交点
B.三角形三条边上高线的交点
C.三角形三条边垂直平分线的交点
D.三角形三条内角平分线的交点
6.下列长度的三条线段能构成三角形的是( )
A.3,4,8
B.3,4,7
C.5,6,10
D.5,6,11
7.如图,△ABC的面积为3,BD:DC=2:1,E是AC的中点,AD与BE相交于点P,那么四边形PDCE的面积为( )
A.
B.
C.
D.
8.下列图形中,具有稳定性的是( )
A.
B.
C.
D.
9.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=76°,∠C=64°,则∠DAE的度数是( )
A.10°
B.12°
C.15°
D.18°
10.如图,直线AB∥CD,∠B=50°,∠D=20°,则∠E的度数是( )
A.20°
B.30°
C.50°
D.70°
二.填空题
11.空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是
.
12.数一数图中共有
个三角形.
13.锐角三角形的三条高都在
,钝角三角形有
条高在三角形外,直角三角形有两条高恰是它的
.
14.如图,在△ABC中,BD=DC,AE=EB,AD与CE相交于点O,若DO=2cm,则AO=
cm.
15.如图,∠α=125°,∠1=50°,则∠β=
.
16.如图,共有
个三角形.
17.阅读材料,并填表:
在△ABC中,有一点P1,当P1,A,B,C没有任何三点在同一直线上时,可构成三个不重叠的小三角形(如图).当△ABC内的点的个数增加时,若其它条件不变,三角形内互不重叠的小三角形的个数情况怎样
完成下表:
ABC内点的个数
1
2
3
…
1002
构成不重叠的小三角形的个数
3
5
…
按表格顺序填入为
,
.
18.已知D、E分别是△ABC的边BC和AC的中点,若△ABC的面积=24cm2,则△DEC的面积为
.
19.设△ABC三边为a、b、c,其中a、b满足|a+b﹣6|+(a﹣b+4)2=0,则第三边c的取值范围
.
20.如图,在直角三角形ABC中,点P、Q分别是AC、BC边上的两个动点,MP、NQ分别平分∠APQ和∠BQP,交AB于点M、N,MR、NR又分别平分∠BMP和∠ANQ,两条角平分线交于点R,则∠R=
°.
三.解答题
21.(1)下列图形中具有稳定性是
;(只填图形序号)
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
22.【数学经验】三角形的中线的性质:三角形的中线等分三角形的面积.
【经验发展】面积比和线段比的联系:
(1)如图1,M为△ABC的AB上一点,且BM=2AM,若△ABC的面积为a,若△CBM的面积为S,则S=
(用含a的代数式表示).
【结论应用】如图2,已知△CDE的面积为1,,,求△ABC的面积.
【迁移应用】如图3,在△ABC中,M是AB的三等分点(AM=AB),N是BC的中点,若△ABC的面积是1,请直接写出四边形BMDN的面积为
.
23.一个三角形有两条边相等,周长为20cm,三角形的一边长6cm,求其他两边长.
24.两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为
个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?
25.观察以下图形,回答问题:
(1)图②有
个三角形;图③有
个三角形;图④有
个三角形;…猜测第七个图形中共有
个三角形.
(2)按上面的方法继续下去,第n个图形中有
个三角形(用含n的代数式表示结论).
26.已知AD是△ABC的高,∠BAD=70°,∠CAD=20°,求∠BAC的度数.
27.如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O.
(1)BO与OD的长度有什么关系?并证明你的结论.
(2)BC边上的中线是否一定过点O?为什么?
参考答案与试题解析
一.选择题
1.解:以BC为边的三角形有△BCE,△BAC,△DBC,
故选:C.
2.解:根据图示知,图中的三角形有:△ABE,△ABC,△DEC,△DBC,△EBC,共有5个.
故选:C.
3.解:根据非负数的性质,a﹣b=0,b﹣c=0,
解得a=b,b=c,
所以,a=b=c,
所以,△ABC是等边三角形.
故选:C.
4.解:由三角形的高线的定义,C选项图形表示△ABC中AC边上的高.
故选:C.
5.解:三角形的重心是三条中线的交点,
故选:A.
6.解:根据三角形任意两边的和大于第三边,得
A中,3+4=7<8,不能组成三角形;
B中,3+4=7,不能组成三角形;
C中,5+6=11>10,能够组成三角形;
D中,5+6=11,不能组成三角形.
故选:C.
7.解:连接CP,
设△CPE的面积是x,△CDP的面积是y.
∵BD:DC=2:1,E为AC的中点,
∴△BDP的面积是2y,△APE的面积是x,
∵BD:DC=2:1,CE:AC=1:2,
∴△ABP的面积是4x.
∴4x+x=2y+x+y,
解得y=x.
又∵4x+x=,
x=.
则四边形PDCE的面积为x+y=.
故选:B.
8.解:根据三角形具有稳定性可得选项B具有稳定性,
故选:B.
9.解:∵AE平分∠BAC,
∴∠CAE=∠CAB=×76°=38°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=90°﹣64°=26°,
∴∠DAE=∠EAC﹣∠CAD=38°﹣26°=12°,
故选:B.
10.解:∵AB∥CD,
∴∠BMD=∠B=50°,
又∵∠BMD是△CDE的外角,
∴∠E=∠BMD﹣∠D=50°﹣20°=30°.
故选:B.
二.填空题
11.解:这种方法应用的数学知识是:三角形的稳定性,
故答案为:三角形具有稳定性.
12.解:线段AD上有4个点,
可以与E组成的三角形有×4×(4﹣1)=6个.
故答案是:6.
13.解:锐角三角形有三条高,高都在三角形内部,且锐角三角形三条高的交点一定在三角形内部;
钝角三角形有三条高,一条高在三角形内部,另外两条高在三角形外部,
直角三角形有两条高即三角形的两条直角边,一条在内部,三条高的交点在顶点上;
故答案分别是:三角形内部;二;直角边.
14.解:∵BD=DC,AE=EB,AD与CE相交于点O,
∴O是△ABC的重心,
∴AO=2DO=2×2=4cm.
故答案为:4.
15.解:∵∠2=∠α﹣∠1=75°,
∴∠β=180°﹣∠2=180°﹣75°=105°.
16.解:图中有:△OAB,△OAC,△OAD,△OBC,△OCD,△OBD,共6个.
故答案为:6.
17.解:当△ABC内的点的个数是n时,三角形内互不重叠的小三角形的个数2n+1.∴按表格顺序填入为7,2005.
18.解:∵D、E分别是△ABC的边BC和AC的中点,
∴S△ABC=2S△ADC
又∵D是△ABC的边BC的中点,S△ABC=24cm2,
∴S△DEC=S△ABC=6cm2.
故答案为:6cm2.
19.解:由题意得:,
解得,
根据三角形的三边关系定理可得5﹣1<c<5+1,
即4<c<6.
故答案为:4<c<6.
20.解:∵∠C+∠A+∠B=180°,∠C+∠CPQ+∠CQP=180°,∠C=90°,
∴∠A+∠B=90°,∠CPQ+∠CQP=90°,
∴∠APQ+∠BQP+∠CPQ+∠CQP=360°,
∴∠APQ+∠BQP=270°,
∵MP、NQ分别平分∠APQ和∠BQP,
∴∠MPQ+∠NQP=∠APM+∠BQN=135°,
∵∠MPQ+∠NQP+∠PMN+∠QNM=360°,
∴∠PMN+∠QNM=225°,
∵MR、NR又分别平分∠BMP和∠ANQ,
∴∠NMR+∠MNR=112.5°,
∵∠NMR+∠MNR+∠R=180°,
∴∠R=67.5°.
故答案为67.5.
三.解答题
21.解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
22.解:(1)∵M为△ABC的AB上一点,且BM=2AM,
∴S=a,
故答案为a;
(2)连接BD,
∵△CDE的面积为1,,
∴S△BDC=3S△DEC=3,
∵,
∴S△ABC=4S△BDC=12;
(3)连接BD,
设S△ADM=a,
∵M是AB的三等分点(AM=AB),
∴S△ABD=3a,S△BDM=2a,
∵N是BC的中点,
∴S△ABN=S△ACN,S△BDN=S△CDN,
∴S△ADC=S△ADB=3a,
∴S△ACM=4a,
∵AM=AB,
∴S△CBM=2S△ACM=8a,
∴S△CDB=6a,S△ABC=12a,
∴S△BDN=3a,
∴S四边形BMDN=5a,
∴S四边形BMDN=S△ABC=×1=,
故答案为.
23.解:(1)当6是腰时,底边=20﹣6×2=8cm,即其它两边是6cm,8cm,此时6+6=12,能构成三角形;
(2)当6是底边时,腰=(20﹣6)÷2=7cm,此时能构成三角形,所以其它两边是7cm、7cm.
因此其它两边长分别为7cm,7cm,
综上所述两边长分别为6cm,8cm或7cm,7cm.
24.解:(1)
4个;
(2)当有n对点时,最少可以画2(n﹣1)个三角形;
(3)2×(2006﹣1)=4010个.
答:当n=2006时,最少可以画4010个三角形.
25.解:(1)图②有3个三角形;图③有5个三角形;图④有7个三角形;…猜测第七个图形中共有13个三角形.
(2)∵图②有3个三角形,3=2×2﹣1;
图③有5个三角形,5=2×3﹣1;
图④有7个三角形,7=2×4﹣1;
∴第n个图形中有(2n﹣1)个三角形.
故答案为3,5,7,13,(2n﹣1).
26.解:①如图1,当高AD在△ABC的内部时,
∠BAC=∠BAD+∠CAD=70°+20°=90°;
②如图2,当高AD在△ABC的外部时,
∠BAC=∠BAD﹣∠CAD=70°﹣20°=50°,
综上所述,∠BAC的度数为90°或50°.
27.解:(1)BO=2OD,理由如下:
连接DE,
∵BD、CE是边AC、AB上的中线,
∴DE∥BC,DE=BC.
∴△ODE~△OBC,
∴=,
即BO=2OD.
(2)BC边上的中线一定过点O,
理由是:作BC边上的中线AF,交BD于M,
连接DF,
∵BD、AF是边AC、BC上的中线,
.∴DF∥BA,DF=BA.
∴△MDF~△MBA
∴===,
即BD=3DM,
BO=BD,
∴O和M重合,
即BC边上的中线一定过点O.
同课章节目录
