2021-2022学年湘教新版七年级上册数学《第2章 代数式》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年湘教新版七年级上册数学《第2章 代数式》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 00:00:00 | ||
图片预览




文档简介
2021-2022学年湘教新版七年级上册数学《第2章
代数式》单元测试卷
一.选择题
1.下列各式符合代数式书写规范的是( )
A.
B.a×3
C.3x﹣1个
D.
2.关于代数式x+1的结果,下列说法一定正确的是( )
A.比1大
B.比1小
C.比x大
D.比x小
3.下列代数式书写规范的是( )
A.a×2
B.2a
C.(5÷3)a
D.2a2
4.已知a﹣7b=﹣2,则4﹣2a+14b的值是( )
A.0
B.2
C.4
D.8
5.当x=﹣2时,ax3+bx﹣7的值为9,则当x=2时,ax3+bx﹣7的值是( )
A.﹣23
B.﹣17
C.23
D.17
6.下列说法正确的是( )
A.单项式是整式,整式也是单项式
B.25与x5是同类项
C.单项式的系数是,次数是4
D.是一次二项式
7.“a的2倍与3的和”用式子表示是( )
A.2a﹣3
B.2a+3
C.2(a+3)
D.3a+2
8.一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23、33和43分别可以“分裂”成2个、3个和4个连续奇数的和,即23=3+5,33=7+9+11,43=13+15+17+19,…若1003也按照此规律来进行“分裂”,则1003“分裂”出的奇数中,最小的奇数是( )
A.9999
B.9910
C.9901
D.9801
9.m表示一个两位数,n表示一个三位数,把m放在n的左边组成一个五位数,那么这个五位数可以表示成( )
A.mn
B.1000m+n
C.100m+1000n
D.100m+n
10.观察下列图形:
它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).
A.4+3(n﹣1)
B.4n
C.4n+1
D.3n+4
二.填空题
11.对代数式“5x”,我们可以这样来解释:某人以5千米/小时的速度走了x小时,他一共走的路程是5x千米.请你对“5x”再给出另一个生活实际方面的解释:
.
12.若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如a+b+c就是完全对称式,下列三个代数式:①a﹣b﹣c;②﹣a﹣b﹣c+2;③ab+bc+ca;④a2b+b2c+c2a,其中是完全对称式的是
.
13.实验中学初三年级12个班中共有团员a人,则表示的实际意义是
.
14.a的2倍与b的差用代数式表示为
.
15.代数式2a2﹣b=7,则10﹣4a2+2b的值是
.
16.将一张长为12.6cm,宽为acm的长方形纸片按图折叠出一个正方形并剪下,称为第一次操作;将余下的长方形纸片再次折叠出一个正方形并剪下,称为第二次操作;如此操作下去,若每一次剪下后的长方形纸片只能折出一个正方形,则当第五次操作后,剩下图形的长与宽之比为2:1,则a的值为
.
17.某种商品n千克的售价是m元,则这种商品8千克的售价是
元.
18.有一列数:,﹣,,﹣,,…按规律第6个数是
;第n个数是
.
19.按图中的程序计算,若输出的值为﹣1,则输入的数为
.
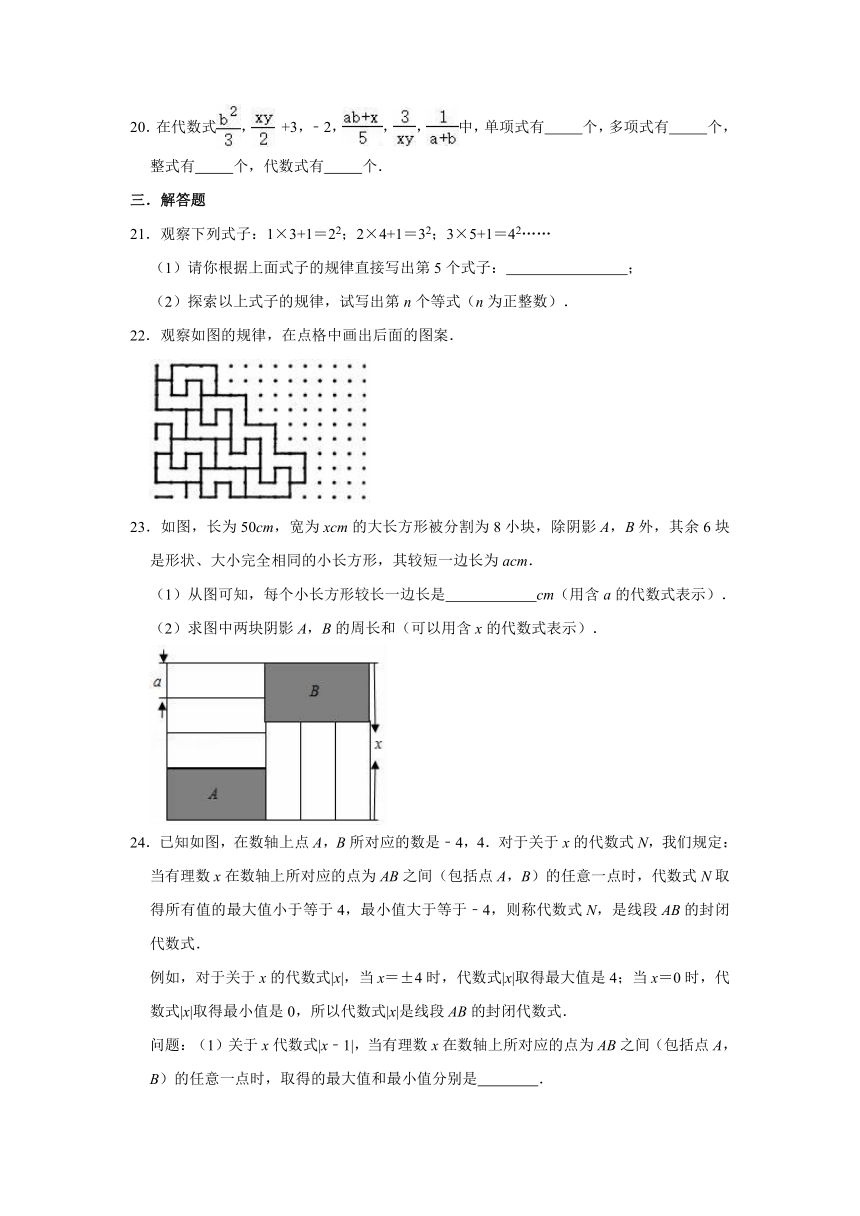
20.在代数式,
+3,﹣2,,,中,单项式有
个,多项式有
个,整式有
个,代数式有
个.
三.解答题
21.观察下列式子:1×3+1=22;2×4+1=32;3×5+1=42……
(1)请你根据上面式子的规律直接写出第5个式子:
;
(2)探索以上式子的规律,试写出第n个等式(n为正整数).
22.观察如图的规律,在点格中画出后面的图案.
23.如图,长为50cm,宽为xcm的大长方形被分割为8小块,除阴影A,B外,其余6块是形状、大小完全相同的小长方形,其较短一边长为acm.
(1)从图可知,每个小长方形较长一边长是
cm(用含a的代数式表示).
(2)求图中两块阴影A,B的周长和(可以用含x的代数式表示).
24.已知如图,在数轴上点A,B所对应的数是﹣4,4.对于关于x的代数式N,我们规定:当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,代数式N取得所有值的最大值小于等于4,最小值大于等于﹣4,则称代数式N,是线段AB的封闭代数式.
例如,对于关于x的代数式|x|,当x=±4时,代数式|x|取得最大值是4;当x=0时,代数式|x|取得最小值是0,所以代数式|x|是线段AB的封闭代数式.
问题:(1)关于x代数式|x﹣1|,当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,取得的最大值和最小值分别是
.
所以代数式|x﹣1|
(填是或不是)线段AB的封闭代数式.
(2)以下关于x的代数式:
①;②x2+1;③x2+|x|﹣8;④|x+2|﹣|x﹣1|﹣1.
是线段AB的封闭代数式是
,并证明(只需要证明是线段AB的封闭代数式的式子,不是的不需证明).
(3)关于x的代数式+3是线段AB的封闭代数式,则有理数a的最大值是
,最小值是
.
25.绝对值拓展材料:|a|表示数a在数轴上的对应点与原点的距离如:|5|表示5在数轴上的对应点到原点的距离而|5|=|5﹣0|,即|5﹣0|表示5、0在数轴上对应的两点之间的距离,类似的,有:|5+3|=|5﹣(﹣3)|表示5、﹣3在数轴上对应的两点之间的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
完成下列题目:
(1)A、B分别为数轴上两点,A点对应的数为﹣2,B点对应的数为4
①A、B两点之间的距离为
;
②折叠数轴,使A点与B点重合,则表示﹣3的点与表示
的点重合;
③若在数轴上存在一点P到A的距离是点P到B的距离的2倍,则点P所表示的数是
;
(2)求|x﹣2|+|x+2|的最小值为
,若满足|x﹣2|+|x+2|=6时,则x的值是
.
26.已知如图,在数轴上点A,B所对应的数是﹣4,4.
对于关于x的代数式N,我们规定:当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,代数式N取得所有值的最大值小于等于4,最小值大于等于﹣4,则称代数式N,是线段AB的吉祥式.
例如,对于关于x的代数式|x|,当x=±4时,代数式|x|取得最大值是4;当x=0时,代数式|x|取得最小值是0,所以代数式|x|是线段AB的吉祥式.
问题:
(1)关于x代数式|x﹣1|,当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,取得的最大值是
,取得的最小值是
;所以代数式|x﹣1|
(填是或不是)线段AB的吉祥式.
(2)以下关于x的代数式:
①x2+1;②|x+2|﹣|x﹣1|﹣1,是线段AB的封闭代数式是
.(填序号)
(3)关于x的代数式|x+1|+2a是线段AB的吉祥式,请求出有理数a的最大值和最小值.
27.在罗山县某住房小区建设中,为了提高业主的宜居环境,某小区规划修建一个广场(平面图如图所示).
(1)用含m、n的代数式表示该广场的面积S;
(2)若m、n满足(m﹣6)2+|n﹣8|=0,求出该广场的面积.
参考答案与试题解析
一.选择题
1.解:A、符合代数式的书写,故A选项正确;
B、中乘号应省略,数字放前面,故B选项错误;
C、中后面有单位的应加括号,故C选项错误;
D、中的带分数应写成假分数,故D选项错误.
故选:A.
2.解:由于1>0,
∴x+1>x,
故选:C.
3.解:选项A正确的书写格式是2a,
B正确的书写格式是a,
C正确的书写格式是a,
D正确.
故选:D.
4.解:∵a﹣7b=﹣2,
∴原式=4﹣2(a﹣7b)=4+4=8,
故选:D.
5.解:∵当x=﹣2时,ax3+bx﹣7的值为9,
∴﹣8b﹣2b=16,
∴8a+2b=﹣16,
当x=2时,原式=8a+2b﹣7=﹣16﹣7=﹣23.
故选:A.
6.解;A、整式包括单项式和多项式,所以单项式是整式,但整式不一定是单项式,故本选项错误;
B、25与x5指数相同,但底数不同,故本选项错误;
C、单项式的系数是,次数是4,正确;
D、中的不是整式,故本选项错误.
故选:C.
7.解:“a的2倍与3的和”用式子表示是:2a+3,
故选:B.
8.解:23=3+5;33=7+9+11;43=13+15+17+19;
∵3=2×1+1,
7=3×2+1,
13=4×3+1,
∴m3“分裂”出的奇数中最小的奇数是m(m﹣1)+1,
∴1003“分裂”出的奇数中最小的奇数是100×99+1=9901,
故选:C.
9.解:∵m表示一个两位数,n表示一个三位数,把m放在n的左边组成一个五位数,
∴相当于把m扩大1000倍,
∴表示这个五位数的代数式1000m+n.
故选:B.
10.解:根据已知图形得:
第1个图形五角星个数:1×3+1,
第2个图形五角星个数:2×3+1,
第3个图形五角星个数:3×3+1,
第4个图形五角星个数:4×3+1,
由此规律得:
第2个图形五角星个数:n×3+1,
故第n个图形中共有3n+1个图形;
A答案为4+3(n﹣1)=3n+1.
故选:A.
二.填空题
11.解:答案不唯一.
如:某人以5个/分钟的效率工作了x分钟,他一共做的零件总数为5x.
12.解:∵把a、b两个字母交换,b﹣a﹣c不一定等于a﹣b﹣c,a2b+b2c+c2a不一定等于b2b+a2c+c2a,
∴①④不符合题意.
∵若将代数式中的任意两个字母交换,代数式不变,
∴②③符合题意.
故答案为:②③.
13.解:表示的实际意义是平均每班团员数.
故答案为:平均每班团员数.
14.解:a的2倍与b的差用代数式表示为2a﹣b,
故答案为:2a﹣b.
15.解:∵2a2﹣b=7,
∴10﹣4a2+2b=10﹣2(2a2﹣b)=10﹣2×7=﹣4.
故答案为:﹣4.
16.解:∵每一次剪下后的长方形纸片只能折出一个正方形,
∴①长:a,宽12.6﹣a;
②长:12.6﹣a,宽2a﹣12.6;
③长:2a﹣12.6,宽25.2﹣3a;
④长:25.2﹣3a,宽5a﹣37.8;
⑤长:5a﹣37.8,宽63﹣8a;
∵第五次操作后,剩下图形的长与宽之比为2:1,
∴5a﹣37.8=2(63﹣8a),
解得:a=7.8,
故答案为:7.8.
17.解:根据题意,得:,
故答案为:.
18.解:∵第n个数为(﹣1)n+1,
∴第6个数是﹣.
故答案为:﹣,(﹣1)n+1.
19.解:设输入的数为x,
根据题意,得:(x﹣6)÷(﹣2)+3=﹣1,
解得:x=14,
故答案为:14.
20.解:根据整式,单项式,多项式的概念可知,单项式有,﹣2,共2个;多项式有+3,,共2个,整式有4个,代数式有6个.
故本题答案为:2;2;4;6.
三.解答题
21.解:(1)∵1×3+1=4=22,
2×4+1=9=32,
3×5+1=16=42,
∴4×6+1=25=52,
5×7+1=36=62,
故答案为5×7+1=36=62;
(2)∵1×3+1=4=22,
2×4+1=9=32,
3×5+1=16=42,
4×6+1=25=52,
5×7+1=36=62,
∴第n个式子表达式为:n(n+2)+1=(n+1)2.
22.解:∵图形是由向上的“凹”字和向下的“凹”字组成,
∴画出图形如下:
.
23.解:(1)每个小长方形较长一边长是(50﹣3a)cm.
故答案为(50﹣3a);
(2)2[50﹣3a+(x﹣3a)]+2[3a+x﹣(50﹣3a)],
=2(50+x﹣6a)+2(6a+x﹣50),
=4x.
24.(1)解:当x=﹣4时,|x﹣1|取得最大值为5,
当x=1时,|x﹣1|取得最小值为0,
∵|x﹣1|的最大值>4,
∴|x﹣1|不是线段AB的封闭代数式.
(2)证明:①∵﹣4≤x≤4,
∵,
∴,
∵的最小值为,不满足最小值大于等于﹣4,
∴不是线段AB的封闭代数式.
②当x=±4时,
代数式x2+1取得最大值17,不满足最大值小于等于4,
∴x2+1不是线段AB的封闭代数式.
③当x=±4时,
代数式x2+|x|﹣8取得最大值12,不满足最大值小于等于4,
∴x2+|x|﹣8不是线段AB的封闭代数式.
④当﹣4≤x<﹣2时,
原式=|x+2|﹣|x﹣1|﹣1=﹣(x+2)+(x﹣1)﹣1=﹣4,
当﹣2≤x≤1时,
原式=|x+2|﹣|x﹣1|﹣1=(x+2)﹣(x﹣1)﹣1=2x,
∴﹣4≤2x≤2,
当1≤x≤4时,
原式=|x+2|﹣|x﹣1|﹣1=(x+2)﹣(x﹣1)﹣1=2,
综上所述:﹣4≤|x+2|﹣|x﹣1|﹣1≤2满足最大值小于等于4,最小值大于等于﹣4,
∴|x+2|﹣|x﹣1|﹣1是线段AB的封闭代数式.
(3)+3≤4,
a≤|x+1|+2,
|x+1|+2在﹣4和4之间的最小值是2,a要不大于这个最小值才能使所有在﹣4和4之间的x都成立,
所以a的最大值是2,
+3≥﹣4,
a≥﹣7(|x+1|+2),
﹣7(|x+1|+2)在﹣4和4之间的最大值是﹣14,a要不小于这个最大值才能使所有在﹣4和4之间的x都成立,
所以a的最小值是﹣14.
故答案为:(1)5,0,不是;(2)④;(3)2;﹣14.
25.解:(1)①A、B两点之间的距离为4﹣(﹣2)=6,
故答案为:6;
②折叠数轴,使A点与B点重合,则折痕为点1,
则表示﹣3的点与表示5的点重合;
故答案为:5;
③分两种情况:当P在AB之间时,P表示的数为2,
当P在B的右侧时,P表示的数为10,
综上,则点P所表示的数是2或10;
故答案为:2或10;
(2)|x﹣2|表示x与2距离,|x+2|表示x与﹣2的距离,所以当表示x的点在2与﹣2之间时,|x﹣2|+|x+2|的值最小,且最小值是4,
|x﹣2|+|x+2|=6,
∴当x<﹣2时,2﹣x﹣x﹣2=6,得x=﹣3,
当﹣2≤x≤2时,2﹣x+x+2=4≠6,故此时无解;
当x>2时,x﹣2+x+2=6,得x=3,
故答案为:±3.
26.解:(1)当x=﹣4时,|x﹣1|取得最大值为5,
当x=1时,|x﹣1|取得最小值为0,
∵|x﹣1|的最大值>4,
∴|x﹣1|不是线段AB的吉祥式.
故答案为:5,0,不是;
(2)当﹣4≤x<﹣2时,
|x+2|﹣|x﹣1|﹣1=﹣(x+2)+(x﹣1)﹣1=﹣4,
当﹣2≤x≤1时,
|x+2|﹣|x﹣1|﹣1=(x+2)﹣(x﹣1)﹣1=2x,
∴﹣4≤2x≤2,
当1≤x≤4时,
原式=|x+2|﹣|x﹣1|﹣1=(x+2)﹣(x﹣1)﹣1=2,
综上所述:﹣4≤|x+2|﹣|x﹣1|﹣1≤2满足最大值小于等于4,最小值大于等于﹣4,|x+2|﹣|x﹣1|﹣1是线段AB的封闭代数式.
故答案为:②;
(3)|x+1|+2a≤4,,在﹣4和4之间的最小值是,a要不大于这个最小值才能使所有在﹣4和4之间的x都成立,所以a的最大值是,
|x+1|+2a≥﹣4,,在﹣4和4之间的最大值是﹣2,a要不小于这个最大值才能使所有在﹣4和4之间的x都成立,所以a的最小值是﹣2.
27.解:(1)S=2m×2n﹣m(2n﹣n﹣0.5n)
=4mn﹣0.5mn
=3.5mn;
(2)由题意得m﹣6=0,n﹣8=0,
∴m=6,n=8,
代入,可得
原式=3.5×6×8=168.
代数式》单元测试卷
一.选择题
1.下列各式符合代数式书写规范的是( )
A.
B.a×3
C.3x﹣1个
D.
2.关于代数式x+1的结果,下列说法一定正确的是( )
A.比1大
B.比1小
C.比x大
D.比x小
3.下列代数式书写规范的是( )
A.a×2
B.2a
C.(5÷3)a
D.2a2
4.已知a﹣7b=﹣2,则4﹣2a+14b的值是( )
A.0
B.2
C.4
D.8
5.当x=﹣2时,ax3+bx﹣7的值为9,则当x=2时,ax3+bx﹣7的值是( )
A.﹣23
B.﹣17
C.23
D.17
6.下列说法正确的是( )
A.单项式是整式,整式也是单项式
B.25与x5是同类项
C.单项式的系数是,次数是4
D.是一次二项式
7.“a的2倍与3的和”用式子表示是( )
A.2a﹣3
B.2a+3
C.2(a+3)
D.3a+2
8.一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23、33和43分别可以“分裂”成2个、3个和4个连续奇数的和,即23=3+5,33=7+9+11,43=13+15+17+19,…若1003也按照此规律来进行“分裂”,则1003“分裂”出的奇数中,最小的奇数是( )
A.9999
B.9910
C.9901
D.9801
9.m表示一个两位数,n表示一个三位数,把m放在n的左边组成一个五位数,那么这个五位数可以表示成( )
A.mn
B.1000m+n
C.100m+1000n
D.100m+n
10.观察下列图形:
它们是按一定规律排列的,依照此规律,第n个图形中共有( )个五角星(n为正整数).
A.4+3(n﹣1)
B.4n
C.4n+1
D.3n+4
二.填空题
11.对代数式“5x”,我们可以这样来解释:某人以5千米/小时的速度走了x小时,他一共走的路程是5x千米.请你对“5x”再给出另一个生活实际方面的解释:
.
12.若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如a+b+c就是完全对称式,下列三个代数式:①a﹣b﹣c;②﹣a﹣b﹣c+2;③ab+bc+ca;④a2b+b2c+c2a,其中是完全对称式的是
.
13.实验中学初三年级12个班中共有团员a人,则表示的实际意义是
.
14.a的2倍与b的差用代数式表示为
.
15.代数式2a2﹣b=7,则10﹣4a2+2b的值是
.
16.将一张长为12.6cm,宽为acm的长方形纸片按图折叠出一个正方形并剪下,称为第一次操作;将余下的长方形纸片再次折叠出一个正方形并剪下,称为第二次操作;如此操作下去,若每一次剪下后的长方形纸片只能折出一个正方形,则当第五次操作后,剩下图形的长与宽之比为2:1,则a的值为
.
17.某种商品n千克的售价是m元,则这种商品8千克的售价是
元.
18.有一列数:,﹣,,﹣,,…按规律第6个数是
;第n个数是
.
19.按图中的程序计算,若输出的值为﹣1,则输入的数为
.
20.在代数式,
+3,﹣2,,,中,单项式有
个,多项式有
个,整式有
个,代数式有
个.
三.解答题
21.观察下列式子:1×3+1=22;2×4+1=32;3×5+1=42……
(1)请你根据上面式子的规律直接写出第5个式子:
;
(2)探索以上式子的规律,试写出第n个等式(n为正整数).
22.观察如图的规律,在点格中画出后面的图案.
23.如图,长为50cm,宽为xcm的大长方形被分割为8小块,除阴影A,B外,其余6块是形状、大小完全相同的小长方形,其较短一边长为acm.
(1)从图可知,每个小长方形较长一边长是
cm(用含a的代数式表示).
(2)求图中两块阴影A,B的周长和(可以用含x的代数式表示).
24.已知如图,在数轴上点A,B所对应的数是﹣4,4.对于关于x的代数式N,我们规定:当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,代数式N取得所有值的最大值小于等于4,最小值大于等于﹣4,则称代数式N,是线段AB的封闭代数式.
例如,对于关于x的代数式|x|,当x=±4时,代数式|x|取得最大值是4;当x=0时,代数式|x|取得最小值是0,所以代数式|x|是线段AB的封闭代数式.
问题:(1)关于x代数式|x﹣1|,当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,取得的最大值和最小值分别是
.
所以代数式|x﹣1|
(填是或不是)线段AB的封闭代数式.
(2)以下关于x的代数式:
①;②x2+1;③x2+|x|﹣8;④|x+2|﹣|x﹣1|﹣1.
是线段AB的封闭代数式是
,并证明(只需要证明是线段AB的封闭代数式的式子,不是的不需证明).
(3)关于x的代数式+3是线段AB的封闭代数式,则有理数a的最大值是
,最小值是
.
25.绝对值拓展材料:|a|表示数a在数轴上的对应点与原点的距离如:|5|表示5在数轴上的对应点到原点的距离而|5|=|5﹣0|,即|5﹣0|表示5、0在数轴上对应的两点之间的距离,类似的,有:|5+3|=|5﹣(﹣3)|表示5、﹣3在数轴上对应的两点之间的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
完成下列题目:
(1)A、B分别为数轴上两点,A点对应的数为﹣2,B点对应的数为4
①A、B两点之间的距离为
;
②折叠数轴,使A点与B点重合,则表示﹣3的点与表示
的点重合;
③若在数轴上存在一点P到A的距离是点P到B的距离的2倍,则点P所表示的数是
;
(2)求|x﹣2|+|x+2|的最小值为
,若满足|x﹣2|+|x+2|=6时,则x的值是
.
26.已知如图,在数轴上点A,B所对应的数是﹣4,4.
对于关于x的代数式N,我们规定:当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,代数式N取得所有值的最大值小于等于4,最小值大于等于﹣4,则称代数式N,是线段AB的吉祥式.
例如,对于关于x的代数式|x|,当x=±4时,代数式|x|取得最大值是4;当x=0时,代数式|x|取得最小值是0,所以代数式|x|是线段AB的吉祥式.
问题:
(1)关于x代数式|x﹣1|,当有理数x在数轴上所对应的点为AB之间(包括点A,B)的任意一点时,取得的最大值是
,取得的最小值是
;所以代数式|x﹣1|
(填是或不是)线段AB的吉祥式.
(2)以下关于x的代数式:
①x2+1;②|x+2|﹣|x﹣1|﹣1,是线段AB的封闭代数式是
.(填序号)
(3)关于x的代数式|x+1|+2a是线段AB的吉祥式,请求出有理数a的最大值和最小值.
27.在罗山县某住房小区建设中,为了提高业主的宜居环境,某小区规划修建一个广场(平面图如图所示).
(1)用含m、n的代数式表示该广场的面积S;
(2)若m、n满足(m﹣6)2+|n﹣8|=0,求出该广场的面积.
参考答案与试题解析
一.选择题
1.解:A、符合代数式的书写,故A选项正确;
B、中乘号应省略,数字放前面,故B选项错误;
C、中后面有单位的应加括号,故C选项错误;
D、中的带分数应写成假分数,故D选项错误.
故选:A.
2.解:由于1>0,
∴x+1>x,
故选:C.
3.解:选项A正确的书写格式是2a,
B正确的书写格式是a,
C正确的书写格式是a,
D正确.
故选:D.
4.解:∵a﹣7b=﹣2,
∴原式=4﹣2(a﹣7b)=4+4=8,
故选:D.
5.解:∵当x=﹣2时,ax3+bx﹣7的值为9,
∴﹣8b﹣2b=16,
∴8a+2b=﹣16,
当x=2时,原式=8a+2b﹣7=﹣16﹣7=﹣23.
故选:A.
6.解;A、整式包括单项式和多项式,所以单项式是整式,但整式不一定是单项式,故本选项错误;
B、25与x5指数相同,但底数不同,故本选项错误;
C、单项式的系数是,次数是4,正确;
D、中的不是整式,故本选项错误.
故选:C.
7.解:“a的2倍与3的和”用式子表示是:2a+3,
故选:B.
8.解:23=3+5;33=7+9+11;43=13+15+17+19;
∵3=2×1+1,
7=3×2+1,
13=4×3+1,
∴m3“分裂”出的奇数中最小的奇数是m(m﹣1)+1,
∴1003“分裂”出的奇数中最小的奇数是100×99+1=9901,
故选:C.
9.解:∵m表示一个两位数,n表示一个三位数,把m放在n的左边组成一个五位数,
∴相当于把m扩大1000倍,
∴表示这个五位数的代数式1000m+n.
故选:B.
10.解:根据已知图形得:
第1个图形五角星个数:1×3+1,
第2个图形五角星个数:2×3+1,
第3个图形五角星个数:3×3+1,
第4个图形五角星个数:4×3+1,
由此规律得:
第2个图形五角星个数:n×3+1,
故第n个图形中共有3n+1个图形;
A答案为4+3(n﹣1)=3n+1.
故选:A.
二.填空题
11.解:答案不唯一.
如:某人以5个/分钟的效率工作了x分钟,他一共做的零件总数为5x.
12.解:∵把a、b两个字母交换,b﹣a﹣c不一定等于a﹣b﹣c,a2b+b2c+c2a不一定等于b2b+a2c+c2a,
∴①④不符合题意.
∵若将代数式中的任意两个字母交换,代数式不变,
∴②③符合题意.
故答案为:②③.
13.解:表示的实际意义是平均每班团员数.
故答案为:平均每班团员数.
14.解:a的2倍与b的差用代数式表示为2a﹣b,
故答案为:2a﹣b.
15.解:∵2a2﹣b=7,
∴10﹣4a2+2b=10﹣2(2a2﹣b)=10﹣2×7=﹣4.
故答案为:﹣4.
16.解:∵每一次剪下后的长方形纸片只能折出一个正方形,
∴①长:a,宽12.6﹣a;
②长:12.6﹣a,宽2a﹣12.6;
③长:2a﹣12.6,宽25.2﹣3a;
④长:25.2﹣3a,宽5a﹣37.8;
⑤长:5a﹣37.8,宽63﹣8a;
∵第五次操作后,剩下图形的长与宽之比为2:1,
∴5a﹣37.8=2(63﹣8a),
解得:a=7.8,
故答案为:7.8.
17.解:根据题意,得:,
故答案为:.
18.解:∵第n个数为(﹣1)n+1,
∴第6个数是﹣.
故答案为:﹣,(﹣1)n+1.
19.解:设输入的数为x,
根据题意,得:(x﹣6)÷(﹣2)+3=﹣1,
解得:x=14,
故答案为:14.
20.解:根据整式,单项式,多项式的概念可知,单项式有,﹣2,共2个;多项式有+3,,共2个,整式有4个,代数式有6个.
故本题答案为:2;2;4;6.
三.解答题
21.解:(1)∵1×3+1=4=22,
2×4+1=9=32,
3×5+1=16=42,
∴4×6+1=25=52,
5×7+1=36=62,
故答案为5×7+1=36=62;
(2)∵1×3+1=4=22,
2×4+1=9=32,
3×5+1=16=42,
4×6+1=25=52,
5×7+1=36=62,
∴第n个式子表达式为:n(n+2)+1=(n+1)2.
22.解:∵图形是由向上的“凹”字和向下的“凹”字组成,
∴画出图形如下:
.
23.解:(1)每个小长方形较长一边长是(50﹣3a)cm.
故答案为(50﹣3a);
(2)2[50﹣3a+(x﹣3a)]+2[3a+x﹣(50﹣3a)],
=2(50+x﹣6a)+2(6a+x﹣50),
=4x.
24.(1)解:当x=﹣4时,|x﹣1|取得最大值为5,
当x=1时,|x﹣1|取得最小值为0,
∵|x﹣1|的最大值>4,
∴|x﹣1|不是线段AB的封闭代数式.
(2)证明:①∵﹣4≤x≤4,
∵,
∴,
∵的最小值为,不满足最小值大于等于﹣4,
∴不是线段AB的封闭代数式.
②当x=±4时,
代数式x2+1取得最大值17,不满足最大值小于等于4,
∴x2+1不是线段AB的封闭代数式.
③当x=±4时,
代数式x2+|x|﹣8取得最大值12,不满足最大值小于等于4,
∴x2+|x|﹣8不是线段AB的封闭代数式.
④当﹣4≤x<﹣2时,
原式=|x+2|﹣|x﹣1|﹣1=﹣(x+2)+(x﹣1)﹣1=﹣4,
当﹣2≤x≤1时,
原式=|x+2|﹣|x﹣1|﹣1=(x+2)﹣(x﹣1)﹣1=2x,
∴﹣4≤2x≤2,
当1≤x≤4时,
原式=|x+2|﹣|x﹣1|﹣1=(x+2)﹣(x﹣1)﹣1=2,
综上所述:﹣4≤|x+2|﹣|x﹣1|﹣1≤2满足最大值小于等于4,最小值大于等于﹣4,
∴|x+2|﹣|x﹣1|﹣1是线段AB的封闭代数式.
(3)+3≤4,
a≤|x+1|+2,
|x+1|+2在﹣4和4之间的最小值是2,a要不大于这个最小值才能使所有在﹣4和4之间的x都成立,
所以a的最大值是2,
+3≥﹣4,
a≥﹣7(|x+1|+2),
﹣7(|x+1|+2)在﹣4和4之间的最大值是﹣14,a要不小于这个最大值才能使所有在﹣4和4之间的x都成立,
所以a的最小值是﹣14.
故答案为:(1)5,0,不是;(2)④;(3)2;﹣14.
25.解:(1)①A、B两点之间的距离为4﹣(﹣2)=6,
故答案为:6;
②折叠数轴,使A点与B点重合,则折痕为点1,
则表示﹣3的点与表示5的点重合;
故答案为:5;
③分两种情况:当P在AB之间时,P表示的数为2,
当P在B的右侧时,P表示的数为10,
综上,则点P所表示的数是2或10;
故答案为:2或10;
(2)|x﹣2|表示x与2距离,|x+2|表示x与﹣2的距离,所以当表示x的点在2与﹣2之间时,|x﹣2|+|x+2|的值最小,且最小值是4,
|x﹣2|+|x+2|=6,
∴当x<﹣2时,2﹣x﹣x﹣2=6,得x=﹣3,
当﹣2≤x≤2时,2﹣x+x+2=4≠6,故此时无解;
当x>2时,x﹣2+x+2=6,得x=3,
故答案为:±3.
26.解:(1)当x=﹣4时,|x﹣1|取得最大值为5,
当x=1时,|x﹣1|取得最小值为0,
∵|x﹣1|的最大值>4,
∴|x﹣1|不是线段AB的吉祥式.
故答案为:5,0,不是;
(2)当﹣4≤x<﹣2时,
|x+2|﹣|x﹣1|﹣1=﹣(x+2)+(x﹣1)﹣1=﹣4,
当﹣2≤x≤1时,
|x+2|﹣|x﹣1|﹣1=(x+2)﹣(x﹣1)﹣1=2x,
∴﹣4≤2x≤2,
当1≤x≤4时,
原式=|x+2|﹣|x﹣1|﹣1=(x+2)﹣(x﹣1)﹣1=2,
综上所述:﹣4≤|x+2|﹣|x﹣1|﹣1≤2满足最大值小于等于4,最小值大于等于﹣4,|x+2|﹣|x﹣1|﹣1是线段AB的封闭代数式.
故答案为:②;
(3)|x+1|+2a≤4,,在﹣4和4之间的最小值是,a要不大于这个最小值才能使所有在﹣4和4之间的x都成立,所以a的最大值是,
|x+1|+2a≥﹣4,,在﹣4和4之间的最大值是﹣2,a要不小于这个最大值才能使所有在﹣4和4之间的x都成立,所以a的最小值是﹣2.
27.解:(1)S=2m×2n﹣m(2n﹣n﹣0.5n)
=4mn﹣0.5mn
=3.5mn;
(2)由题意得m﹣6=0,n﹣8=0,
∴m=6,n=8,
代入,可得
原式=3.5×6×8=168.
同课章节目录
