2021-2022学年青岛新版八年级上册数学《第2章 图形的轴对称》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年青岛新版八年级上册数学《第2章 图形的轴对称》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 313.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 00:00:00 | ||
图片预览


文档简介
2021-2022学年青岛新版八年级上册数学《第2章
图形的轴对称》单元测试卷
一.选择题
1.如果一个三角形是轴对称图形,且有一个内角是60°,那么这个三角形是( )
A.等边三角形
B.等腰直角三角形
C.等腰三角形
D.含30°角的直角三角形
2.圆是轴对称图形,它的对称轴有( )
A.1条
B.2条
C.3条
D.无数条
3.下列说法错误的是( )
A.关于某直线成轴对称的两个图形一定能完全重合
B.线段是轴对称图形
C.全等的两个三角形一定关于某直线成轴对称
D.轴对称图形的对称轴至少有一条
4.点A(﹣2,3)关于x轴的对称点A′的坐标为( )
A.(2,﹣3)
B.(﹣2,﹣3)
C.(﹣2,3)
D.(
2,3)
5.如图,点D为△ABC边AB的中点,将△ABC沿经过点D的直线折叠,使点A刚好落在BC边上的点F处,若∠B=48°,则∠BDF的度数为( )
A.88°
B.86°
C.84°
D.82°
6.用两个全等的直角三角形拼成下列图形:①平行四边形;②矩形;③菱形;④正方形;⑤等腰三角形;⑥等边三角形.则一定可以拼成的图形是( )
A.①④⑤
B.②⑤⑥
C.①②③
D.①②⑤
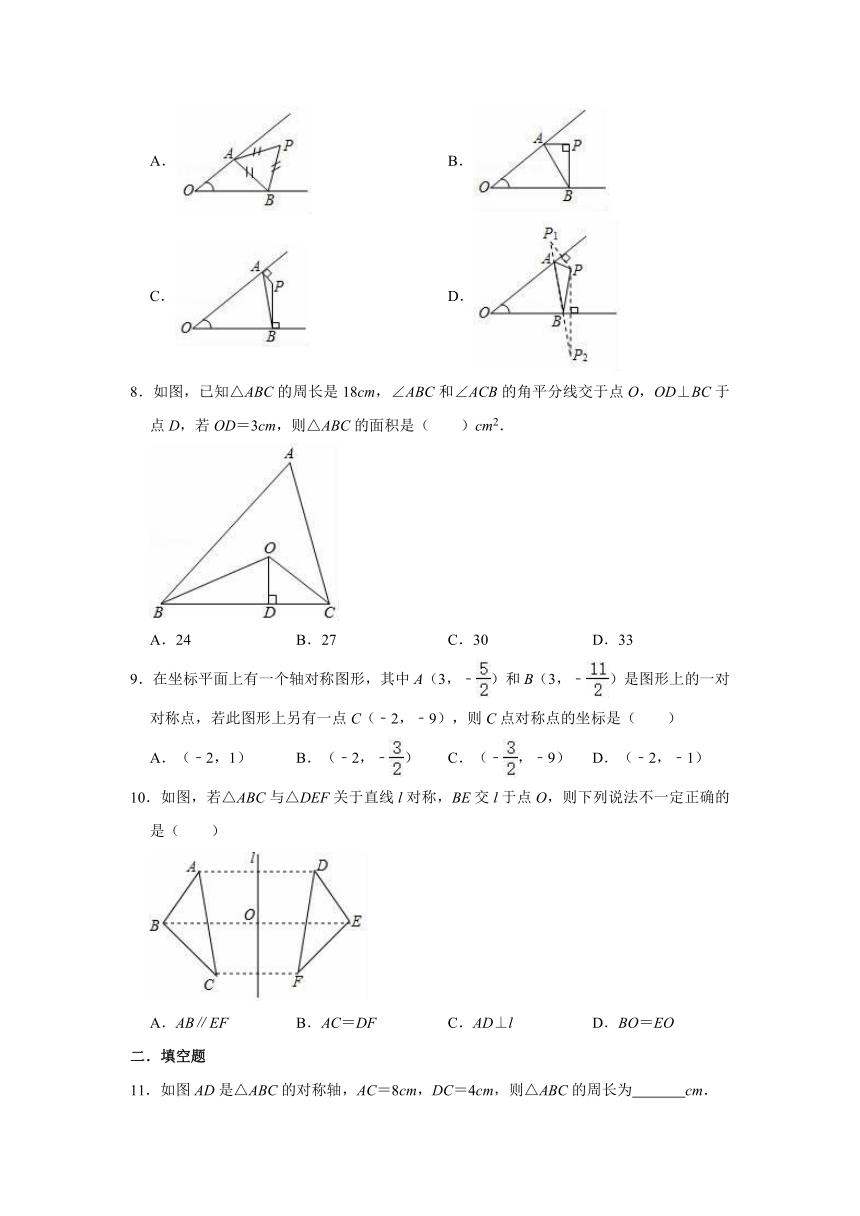
7.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A.
B.
C.
D.
8.如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.
A.24
B.27
C.30
D.33
9.在坐标平面上有一个轴对称图形,其中A(3,﹣)和B(3,﹣)是图形上的一对对称点,若此图形上另有一点C(﹣2,﹣9),则C点对称点的坐标是( )
A.(﹣2,1)
B.(﹣2,﹣)
C.(﹣,﹣9)
D.(﹣2,﹣1)
10.如图,若△ABC与△DEF关于直线l对称,BE交l于点O,则下列说法不一定正确的是( )
A.AB∥EF
B.AC=DF
C.AD⊥l
D.BO=EO
二.填空题
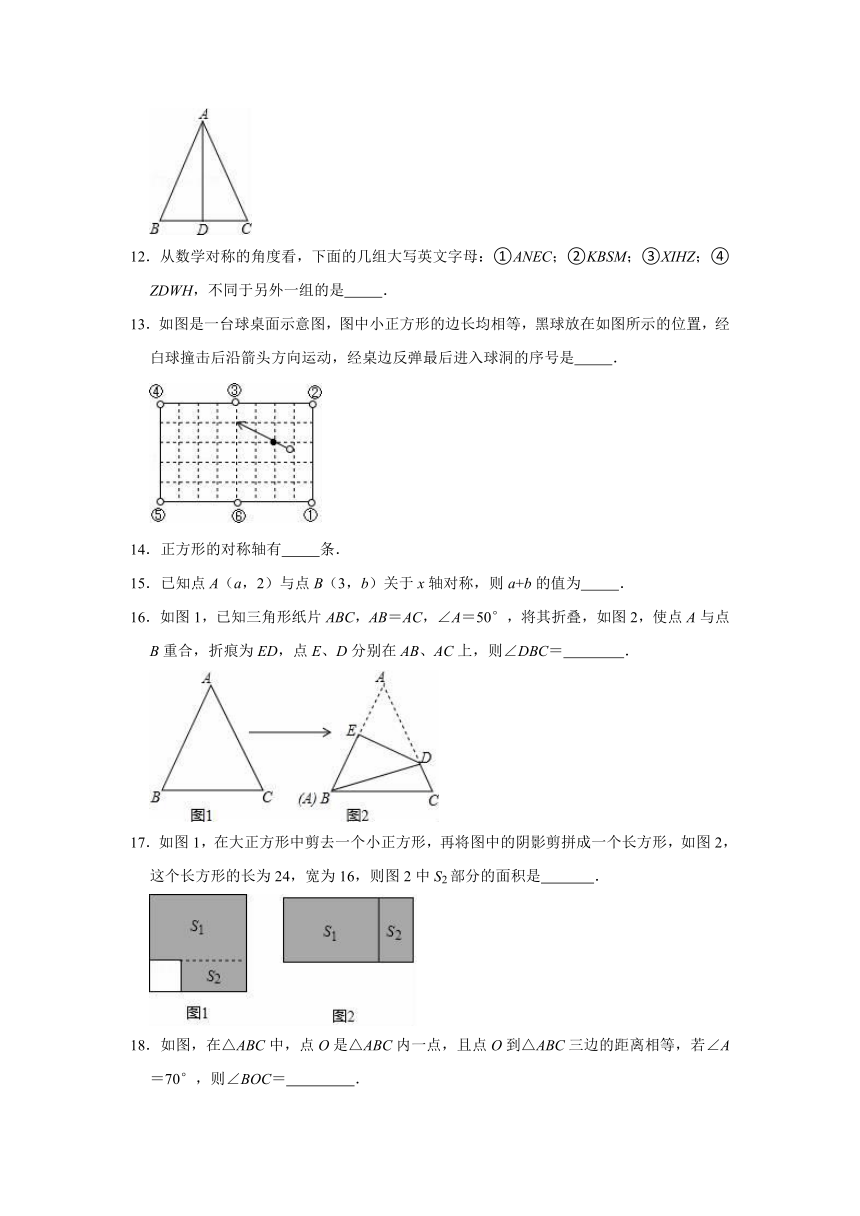
11.如图AD是△ABC的对称轴,AC=8cm,DC=4cm,则△ABC的周长为
cm.
12.从数学对称的角度看,下面的几组大写英文字母:①ANEC;②KBSM;③XIHZ;④ZDWH,不同于另外一组的是
.
13.如图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是
.
14.正方形的对称轴有
条.
15.已知点A(a,2)与点B(3,b)关于x轴对称,则a+b的值为
.
16.如图1,已知三角形纸片ABC,AB=AC,∠A=50°,将其折叠,如图2,使点A与点B重合,折痕为ED,点E、D分别在AB、AC上,则∠DBC=
.
17.如图1,在大正方形中剪去一个小正方形,再将图中的阴影剪拼成一个长方形,如图2,这个长方形的长为24,宽为16,则图2中S2部分的面积是
.
18.如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等,若∠A=70°,则∠BOC=
.
19.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2019次变换后所得的A点坐标是
.
20.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为
三.解答题
21.如图,△ABC的点C与C′关于AB对称,点B与B′关于AC对称,连接BB′、CC′,交于点O.
(1)如图(1),若∠BAC=30°,
①求∠B'AC'的度数;
②观察并描述:△ABC'可以由△AB'C通过什么变换得来?求出∠BOC'的角度;
(2)如图(2),若∠BAC=α,点D、E分别在AB、AC上,且C′D∥BC∥B′E,BE、CD交于点F,设∠BFD=β,试探索α与β之间的数量关系,并说明理由.
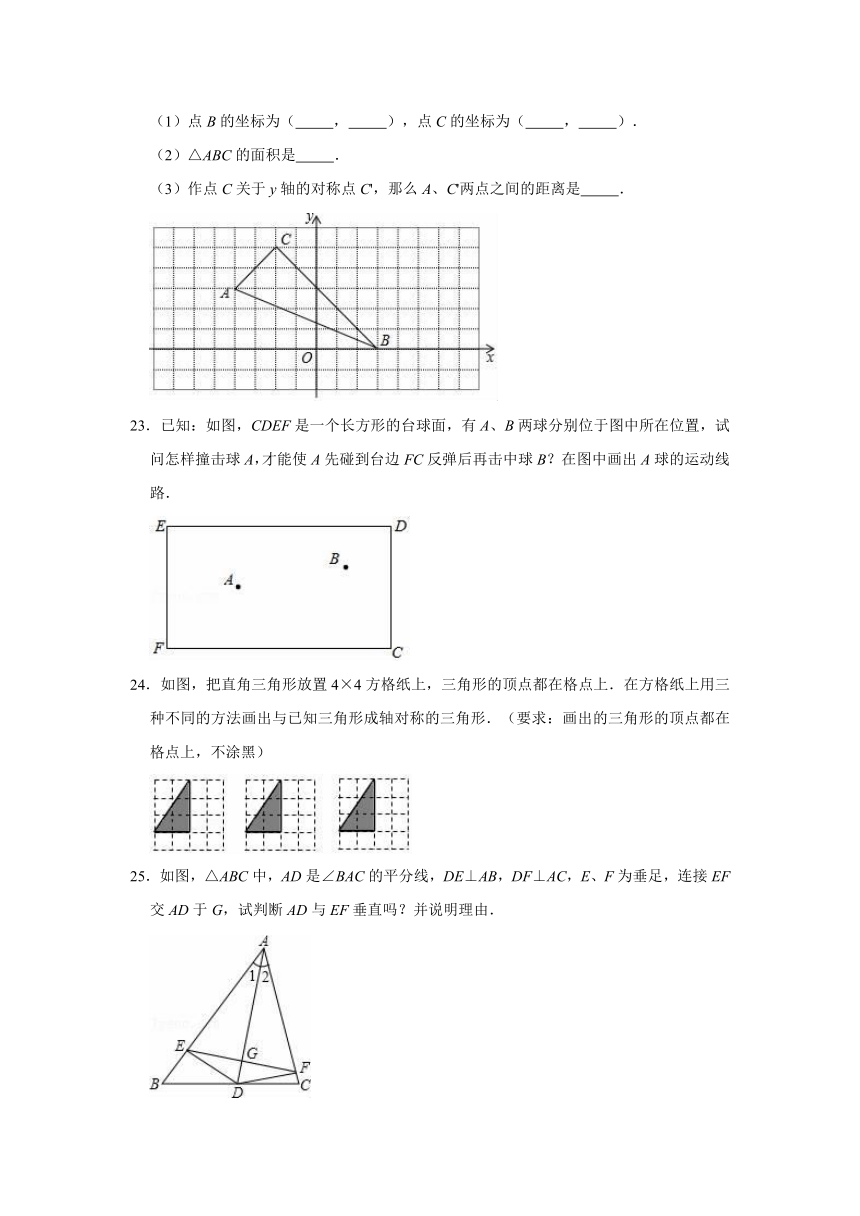
22.在平面直角坐标系中,△ABC的位置如图所示,已知点A的坐标是(﹣4,3).
(1)点B的坐标为(
,
),点C的坐标为(
,
).
(2)△ABC的面积是
.
(3)作点C关于y轴的对称点C',那么A、C'两点之间的距离是
.
23.已知:如图,CDEF是一个长方形的台球面,有A、B两球分别位于图中所在位置,试问怎样撞击球A,才能使A先碰到台边FC反弹后再击中球B?在图中画出A球的运动线路.
24.如图,把直角三角形放置4×4方格纸上,三角形的顶点都在格点上.在方格纸上用三种不同的方法画出与已知三角形成轴对称的三角形.(要求:画出的三角形的顶点都在格点上,不涂黑)
25.如图,△ABC中,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,E、F为垂足,连接EF交AD于G,试判断AD与EF垂直吗?并说明理由.
26.如图,长方形台球桌ABCD上有两个球P,Q.
(1)请画出一条路径,使得球P撞击台球桌边AB反弹后,正好撞到球Q;
(2)请画出一条路径,使得球P撞击台球桌边,经过两次反弹后,正好撞到球Q;
27.如图,若将△ABC顶点横坐标增加4个单位,纵坐标不变,三角形将如何变化?若将△ABC顶点横坐标都乘以﹣1,纵坐标不变,三角形将如何变化?
参考答案与试题解析
一.选择题
1.解:因为三角形是轴对称图形,则该三角形是等腰三角形,
根据有一个内角是60°的等腰三角形是等边三角形.
故选:A.
2.解:圆的对称轴是经过圆心的直线,有无数条.
故选:D.
3.解:A、关于某直线成轴对称的两个图形一定能完全重合,正确,故本选项错误;
B、线段是轴对称图形,正确,故本选项错误;
C、全等的两个三角形不一定关于某直线成轴对称,但关于某直线成轴对称的两个三角形一定,故本选项正确;
D、轴对称图形的对称轴至少有一条,正确,故本选项错误.
故选:C.
4.解:A(﹣2,3)关于x轴的对称点A′的坐标为(﹣2,﹣3);
故选:B.
5.解:由题意得:
DF=DA,
而DB=DA,
∴DF=DB,
∴∠DFB=∠B=48°,
∴∠BDF=180°﹣2×48°=84°,
即∠BDF的度数为84°,
故选:C.
6.解:根据题意,用形状和大小完全相同的直角三角形一定能拼出平行四边形、矩形和等腰三角形,共3种图形.
画出图形如下所示:
故选:D.
7.解:分别在∠O的两边上找点A、B,使△PAB周长最小的是D选项,
故选:D.
8.解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
∵OB平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=3,
同理可得OF=OD=3,
∴S△ABC=S△OAB+S△OBC+S△OAC
=×OE×AB+×OD×BC+×OF×AC
=(AB+BC+AC),
∵△ABC的周长是18,
∴S△ABC=×18=27(cm2).
故选:B.
9.解:∵A(3,﹣)和B(3,﹣)是图形上的一对对称点,
∴点A与点B关于直线y=﹣4对称,
∴点C(﹣2,﹣9)关于直线y=﹣4的对称点的坐标为(﹣2,1).
故选:A.
10.解:∵△ABC与△DEF关于直线l对称,
∴AC=DF,AD⊥l,BO=EO,故D、B、C选项正确,
AB∥EF不一定成立,故A选项错误,
所以,不一定正确的是A.
故选:A.
二.填空题
11.解:∵AD是△ABC的对称轴,
∴BD=CD=4cm,
BC=BD+CD=8cm
AB=AC=8cm,
∴△ABC的周长为=AB+AC+BC=24cm.
12.解:③XIHZ中全是中心对称;
所以而其它选项都有一个以上非中心对称图形.
故应填③.
13.解:如图,求最后落入①球洞;
故答案为:①.
14.解:如图,正方形对称轴为经过对边中点的直线,两条对角线所在的直线,共4条.
故答案为:4.
15.解:∵点A(a,2)与点B(3,b)关于x轴对称,
∴a=3,b=﹣2,
∴a+b=1,
故答案为:1.
16.解:∵△ABC中,AB=AC,∠A=50°,
∴∠ABC==65°.
∵△EBD由△EAD折叠而成,
∴∠EBD=∠A=50°,
∴∠DAB=∠ABC﹣∠EBD=65°﹣50°=15°.
故答案为:15°.
17.解:设大正方形的边长为a,小正方形的边长为b,
根据题意得出:,
解得:,
故图2中S2部分的面积是:4×(20﹣4)=64,
故答案为:64.
18.解:∵在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等,
∴O为△ABC的三内角平分线的交点,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠A=70°,
∴∠ABC+∠ACB=180°﹣∠A=110°,
∴∠OBC+∠OCB=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=125°,
故答案为:125°.
19.解:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2019÷4=504余3,
∴经过第2019次变换后所得的A点与第三次变换的位置相同,在第二象限,坐标为(﹣a,b).
故答案为:(﹣a,b)
20.解:如图所示:在AB上取点F′,使AF′=AF,过点C作CH⊥AB,垂足为H.
在Rt△ABC中,依据勾股定理可知BA=10.
CH=,
∵EF+CE=EF′+EC,
∴当C、E、F′共线,且点F′与H重合时,FE+EC的值最小,最小值为,
故答案为:
三.解答题
21.解:(1)①∵C,C′关于AB对称,B,B′关于AC对称,
∴∠CAB=∠BAC′=∠CAB′=30°,
∴∠B′AC′=90°.
②如图(1)中,设AC交BB′于J.
△ABC'可以由△AB'C绕点A顺时针旋转60°得到.
∵AC=AC′,AB=AB′,∠CAC′=∠BAB′=60°,
∴∠AB′A=∠ACO=60°,
∵∠AJB′=∠OJC,
∴∠B′OC=∠B′AJ=30°.
(2)如图(2)中,结论:β=2α.
理由:由对称的性质可知:BC=BC′,DC′=DC,∠ABC′=∠ABC,
∵DC′∥BC,
∴∠C′DB=∠ABC=∠C′BD,
∴C′D=C′B,
∴BC=BC′=C′D=DC,
∴四边形BCDC′是菱形,
∴CD∥BC′,同法可证,BE∥CB′,
∴∠FCB+∠CBC′=180°,即∠FCB+2∠ABC=180°,
同法可得,∠FBC+2∠ACB=180°,
∵∠BFD=∠FBC+∠FCB,
∴∠DFB=180°﹣2∠ABC+180°﹣2∠ACB=360°﹣2(∠ABC+∠ACB)=360°﹣2(180°﹣∠BAC)=2∠BAC,
∴β=2α.
22.解:(1)点B的坐标为(3,0),点C的坐标为(﹣2,5),
故答案为:3;0;﹣2;5;
(2))△ABC的面积是:7×5﹣3×7﹣2×2﹣×5×5=35﹣10.5﹣2﹣12.5=10,
故答案为:10;
(3)A、C'两点之间的距离是:==2,
故答案为:2.
23.解:如图所示:运动路线:A→P→B.
24.解:如图1,2,3所示,即为所求;.
25.解:AD⊥EF.理由如下:
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△AED和Rt△AFD中,
∵,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵AD平分∠EAF,
∴AD⊥EF(等腰三角形三线合一).
26.解:(1)如图,运动路径:P→M→Q,点M即为所求.
(2)如图,运动路径:P→E→F→Q,点E,点F即为所求.
27.解:横坐标增加4个单位,纵坐标不变,所得各顶点的坐标依次是A(1,3),B(1,1),C(3,1),连接AB、AC、BC,整个三角形向右平移4个单位;
横坐标都乘以﹣1,纵坐标不变,所得各顶点的坐标依次是A(3,3),B(3,1),C(1,1),连接AB、AC、BC,所得到的三角形与原三角形关于y轴对称.
图形的轴对称》单元测试卷
一.选择题
1.如果一个三角形是轴对称图形,且有一个内角是60°,那么这个三角形是( )
A.等边三角形
B.等腰直角三角形
C.等腰三角形
D.含30°角的直角三角形
2.圆是轴对称图形,它的对称轴有( )
A.1条
B.2条
C.3条
D.无数条
3.下列说法错误的是( )
A.关于某直线成轴对称的两个图形一定能完全重合
B.线段是轴对称图形
C.全等的两个三角形一定关于某直线成轴对称
D.轴对称图形的对称轴至少有一条
4.点A(﹣2,3)关于x轴的对称点A′的坐标为( )
A.(2,﹣3)
B.(﹣2,﹣3)
C.(﹣2,3)
D.(
2,3)
5.如图,点D为△ABC边AB的中点,将△ABC沿经过点D的直线折叠,使点A刚好落在BC边上的点F处,若∠B=48°,则∠BDF的度数为( )
A.88°
B.86°
C.84°
D.82°
6.用两个全等的直角三角形拼成下列图形:①平行四边形;②矩形;③菱形;④正方形;⑤等腰三角形;⑥等边三角形.则一定可以拼成的图形是( )
A.①④⑤
B.②⑤⑥
C.①②③
D.①②⑤
7.如图,已知∠O,点P为其内一定点,分别在∠O的两边上找点A、B,使△PAB周长最小的是( )
A.
B.
C.
D.
8.如图,已知△ABC的周长是18cm,∠ABC和∠ACB的角平分线交于点O,OD⊥BC于点D,若OD=3cm,则△ABC的面积是( )cm2.
A.24
B.27
C.30
D.33
9.在坐标平面上有一个轴对称图形,其中A(3,﹣)和B(3,﹣)是图形上的一对对称点,若此图形上另有一点C(﹣2,﹣9),则C点对称点的坐标是( )
A.(﹣2,1)
B.(﹣2,﹣)
C.(﹣,﹣9)
D.(﹣2,﹣1)
10.如图,若△ABC与△DEF关于直线l对称,BE交l于点O,则下列说法不一定正确的是( )
A.AB∥EF
B.AC=DF
C.AD⊥l
D.BO=EO
二.填空题
11.如图AD是△ABC的对称轴,AC=8cm,DC=4cm,则△ABC的周长为
cm.
12.从数学对称的角度看,下面的几组大写英文字母:①ANEC;②KBSM;③XIHZ;④ZDWH,不同于另外一组的是
.
13.如图是一台球桌面示意图,图中小正方形的边长均相等,黑球放在如图所示的位置,经白球撞击后沿箭头方向运动,经桌边反弹最后进入球洞的序号是
.
14.正方形的对称轴有
条.
15.已知点A(a,2)与点B(3,b)关于x轴对称,则a+b的值为
.
16.如图1,已知三角形纸片ABC,AB=AC,∠A=50°,将其折叠,如图2,使点A与点B重合,折痕为ED,点E、D分别在AB、AC上,则∠DBC=
.
17.如图1,在大正方形中剪去一个小正方形,再将图中的阴影剪拼成一个长方形,如图2,这个长方形的长为24,宽为16,则图2中S2部分的面积是
.
18.如图,在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等,若∠A=70°,则∠BOC=
.
19.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2019次变换后所得的A点坐标是
.
20.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为
三.解答题
21.如图,△ABC的点C与C′关于AB对称,点B与B′关于AC对称,连接BB′、CC′,交于点O.
(1)如图(1),若∠BAC=30°,
①求∠B'AC'的度数;
②观察并描述:△ABC'可以由△AB'C通过什么变换得来?求出∠BOC'的角度;
(2)如图(2),若∠BAC=α,点D、E分别在AB、AC上,且C′D∥BC∥B′E,BE、CD交于点F,设∠BFD=β,试探索α与β之间的数量关系,并说明理由.
22.在平面直角坐标系中,△ABC的位置如图所示,已知点A的坐标是(﹣4,3).
(1)点B的坐标为(
,
),点C的坐标为(
,
).
(2)△ABC的面积是
.
(3)作点C关于y轴的对称点C',那么A、C'两点之间的距离是
.
23.已知:如图,CDEF是一个长方形的台球面,有A、B两球分别位于图中所在位置,试问怎样撞击球A,才能使A先碰到台边FC反弹后再击中球B?在图中画出A球的运动线路.
24.如图,把直角三角形放置4×4方格纸上,三角形的顶点都在格点上.在方格纸上用三种不同的方法画出与已知三角形成轴对称的三角形.(要求:画出的三角形的顶点都在格点上,不涂黑)
25.如图,△ABC中,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,E、F为垂足,连接EF交AD于G,试判断AD与EF垂直吗?并说明理由.
26.如图,长方形台球桌ABCD上有两个球P,Q.
(1)请画出一条路径,使得球P撞击台球桌边AB反弹后,正好撞到球Q;
(2)请画出一条路径,使得球P撞击台球桌边,经过两次反弹后,正好撞到球Q;
27.如图,若将△ABC顶点横坐标增加4个单位,纵坐标不变,三角形将如何变化?若将△ABC顶点横坐标都乘以﹣1,纵坐标不变,三角形将如何变化?
参考答案与试题解析
一.选择题
1.解:因为三角形是轴对称图形,则该三角形是等腰三角形,
根据有一个内角是60°的等腰三角形是等边三角形.
故选:A.
2.解:圆的对称轴是经过圆心的直线,有无数条.
故选:D.
3.解:A、关于某直线成轴对称的两个图形一定能完全重合,正确,故本选项错误;
B、线段是轴对称图形,正确,故本选项错误;
C、全等的两个三角形不一定关于某直线成轴对称,但关于某直线成轴对称的两个三角形一定,故本选项正确;
D、轴对称图形的对称轴至少有一条,正确,故本选项错误.
故选:C.
4.解:A(﹣2,3)关于x轴的对称点A′的坐标为(﹣2,﹣3);
故选:B.
5.解:由题意得:
DF=DA,
而DB=DA,
∴DF=DB,
∴∠DFB=∠B=48°,
∴∠BDF=180°﹣2×48°=84°,
即∠BDF的度数为84°,
故选:C.
6.解:根据题意,用形状和大小完全相同的直角三角形一定能拼出平行四边形、矩形和等腰三角形,共3种图形.
画出图形如下所示:
故选:D.
7.解:分别在∠O的两边上找点A、B,使△PAB周长最小的是D选项,
故选:D.
8.解:过O点作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
∵OB平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=3,
同理可得OF=OD=3,
∴S△ABC=S△OAB+S△OBC+S△OAC
=×OE×AB+×OD×BC+×OF×AC
=(AB+BC+AC),
∵△ABC的周长是18,
∴S△ABC=×18=27(cm2).
故选:B.
9.解:∵A(3,﹣)和B(3,﹣)是图形上的一对对称点,
∴点A与点B关于直线y=﹣4对称,
∴点C(﹣2,﹣9)关于直线y=﹣4的对称点的坐标为(﹣2,1).
故选:A.
10.解:∵△ABC与△DEF关于直线l对称,
∴AC=DF,AD⊥l,BO=EO,故D、B、C选项正确,
AB∥EF不一定成立,故A选项错误,
所以,不一定正确的是A.
故选:A.
二.填空题
11.解:∵AD是△ABC的对称轴,
∴BD=CD=4cm,
BC=BD+CD=8cm
AB=AC=8cm,
∴△ABC的周长为=AB+AC+BC=24cm.
12.解:③XIHZ中全是中心对称;
所以而其它选项都有一个以上非中心对称图形.
故应填③.
13.解:如图,求最后落入①球洞;
故答案为:①.
14.解:如图,正方形对称轴为经过对边中点的直线,两条对角线所在的直线,共4条.
故答案为:4.
15.解:∵点A(a,2)与点B(3,b)关于x轴对称,
∴a=3,b=﹣2,
∴a+b=1,
故答案为:1.
16.解:∵△ABC中,AB=AC,∠A=50°,
∴∠ABC==65°.
∵△EBD由△EAD折叠而成,
∴∠EBD=∠A=50°,
∴∠DAB=∠ABC﹣∠EBD=65°﹣50°=15°.
故答案为:15°.
17.解:设大正方形的边长为a,小正方形的边长为b,
根据题意得出:,
解得:,
故图2中S2部分的面积是:4×(20﹣4)=64,
故答案为:64.
18.解:∵在△ABC中,点O是△ABC内一点,且点O到△ABC三边的距离相等,
∴O为△ABC的三内角平分线的交点,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∵∠A=70°,
∴∠ABC+∠ACB=180°﹣∠A=110°,
∴∠OBC+∠OCB=55°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=125°,
故答案为:125°.
19.解:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2019÷4=504余3,
∴经过第2019次变换后所得的A点与第三次变换的位置相同,在第二象限,坐标为(﹣a,b).
故答案为:(﹣a,b)
20.解:如图所示:在AB上取点F′,使AF′=AF,过点C作CH⊥AB,垂足为H.
在Rt△ABC中,依据勾股定理可知BA=10.
CH=,
∵EF+CE=EF′+EC,
∴当C、E、F′共线,且点F′与H重合时,FE+EC的值最小,最小值为,
故答案为:
三.解答题
21.解:(1)①∵C,C′关于AB对称,B,B′关于AC对称,
∴∠CAB=∠BAC′=∠CAB′=30°,
∴∠B′AC′=90°.
②如图(1)中,设AC交BB′于J.
△ABC'可以由△AB'C绕点A顺时针旋转60°得到.
∵AC=AC′,AB=AB′,∠CAC′=∠BAB′=60°,
∴∠AB′A=∠ACO=60°,
∵∠AJB′=∠OJC,
∴∠B′OC=∠B′AJ=30°.
(2)如图(2)中,结论:β=2α.
理由:由对称的性质可知:BC=BC′,DC′=DC,∠ABC′=∠ABC,
∵DC′∥BC,
∴∠C′DB=∠ABC=∠C′BD,
∴C′D=C′B,
∴BC=BC′=C′D=DC,
∴四边形BCDC′是菱形,
∴CD∥BC′,同法可证,BE∥CB′,
∴∠FCB+∠CBC′=180°,即∠FCB+2∠ABC=180°,
同法可得,∠FBC+2∠ACB=180°,
∵∠BFD=∠FBC+∠FCB,
∴∠DFB=180°﹣2∠ABC+180°﹣2∠ACB=360°﹣2(∠ABC+∠ACB)=360°﹣2(180°﹣∠BAC)=2∠BAC,
∴β=2α.
22.解:(1)点B的坐标为(3,0),点C的坐标为(﹣2,5),
故答案为:3;0;﹣2;5;
(2))△ABC的面积是:7×5﹣3×7﹣2×2﹣×5×5=35﹣10.5﹣2﹣12.5=10,
故答案为:10;
(3)A、C'两点之间的距离是:==2,
故答案为:2.
23.解:如图所示:运动路线:A→P→B.
24.解:如图1,2,3所示,即为所求;.
25.解:AD⊥EF.理由如下:
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△AED和Rt△AFD中,
∵,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∵AD平分∠EAF,
∴AD⊥EF(等腰三角形三线合一).
26.解:(1)如图,运动路径:P→M→Q,点M即为所求.
(2)如图,运动路径:P→E→F→Q,点E,点F即为所求.
27.解:横坐标增加4个单位,纵坐标不变,所得各顶点的坐标依次是A(1,3),B(1,1),C(3,1),连接AB、AC、BC,整个三角形向右平移4个单位;
横坐标都乘以﹣1,纵坐标不变,所得各顶点的坐标依次是A(3,3),B(3,1),C(1,1),连接AB、AC、BC,所得到的三角形与原三角形关于y轴对称.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
