2021-2022学年青岛新版七年级上册数学《第1章 基本的几何图形》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年青岛新版七年级上册数学《第1章 基本的几何图形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 282.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-18 22:20:02 | ||
图片预览

文档简介
2021-2022学年青岛新版七年级上册数学《第1章
基本的几何图形》单元测试卷
一.选择题
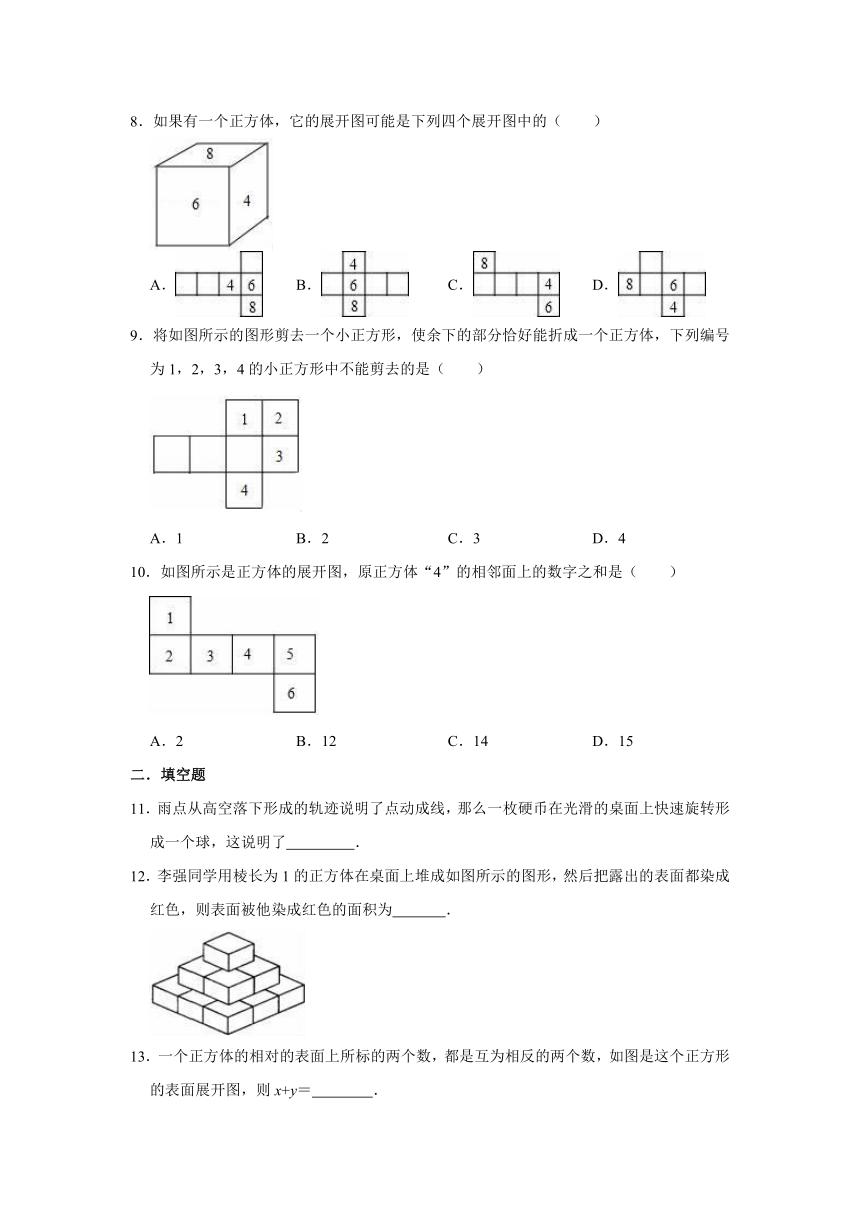
1.下面几何体中,全是由曲面围成的是( )
A.圆柱
B.圆锥
C.球
D.正方体
2.某同学用牙膏纸盒制作一个如图所示的笔筒,笔筒的筒底为长4.5厘米,宽3.4厘米的矩形.则该笔筒最多能放半径为0.4厘米的圆柱形铅笔( )
A.20支
B.21支
C.22支
D.25支
3.在下列图形中,是平面上曲线图形的有( )个
①三角形②正方形③长方形④圆.
A.1
B.2
C.3
D.4
4.在一个正方体的玻璃容器内装了一些水,把容器按不同方式倾斜,容器内水面的形状不可能是以下哪些图形( )
A.锐角三角形
B.钝角三角形
C.等腰梯形
D.五边形
5.将下面四个图形绕着虚线旋转一周,能够得到如图所说的
立体图形的是( )
A.
B.
C.
D.
6.下面几何体中,不能由一个平面图形通过旋转得到的是( )
A.
B.
C.
D.
7.下列的立体图形中,有4个面的是( )
A.三棱锥
B.三棱柱
C.四棱锥
D.四棱柱
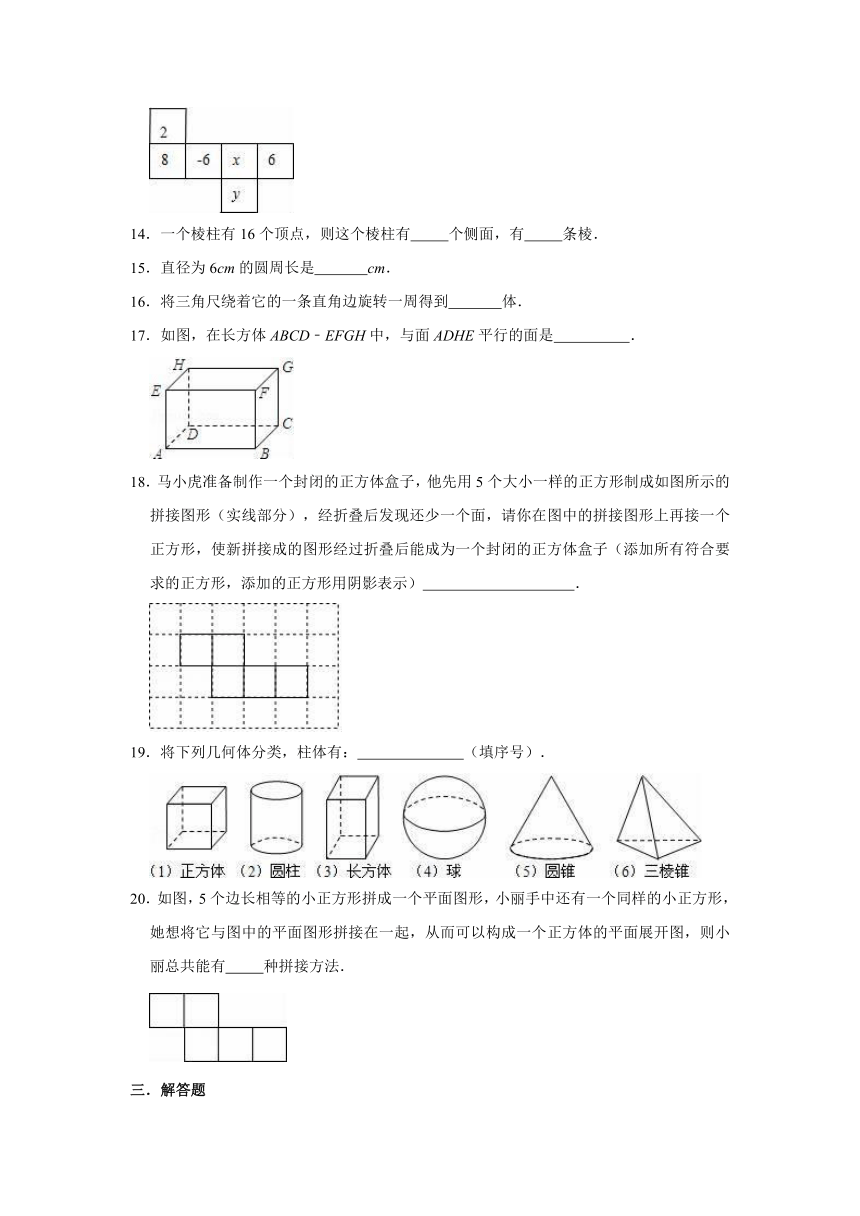
8.如果有一个正方体,它的展开图可能是下列四个展开图中的( )
A.
B.
C.
D.
9.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下列编号为1,2,3,4的小正方形中不能剪去的是( )
A.1
B.2
C.3
D.4
10.如图所示是正方体的展开图,原正方体“4”的相邻面上的数字之和是( )
A.2
B.12
C.14
D.15
二.填空题
11.雨点从高空落下形成的轨迹说明了点动成线,那么一枚硬币在光滑的桌面上快速旋转形成一个球,这说明了
.
12.李强同学用棱长为1的正方体在桌面上堆成如图所示的图形,然后把露出的表面都染成红色,则表面被他染成红色的面积为
.
13.一个正方体的相对的表面上所标的两个数,都是互为相反的两个数,如图是这个正方形的表面展开图,则x+y=
.
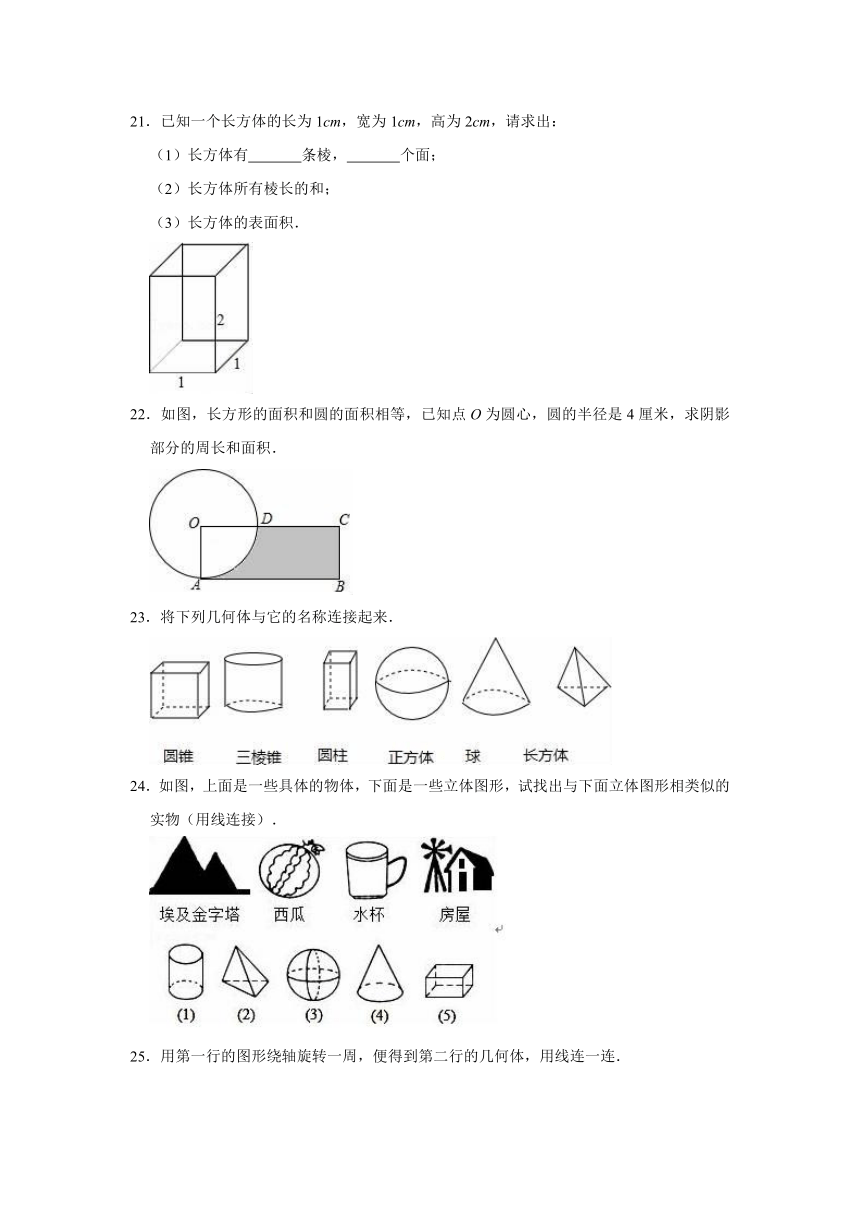
14.一个棱柱有16个顶点,则这个棱柱有
个侧面,有
条棱.
15.直径为6cm的圆周长是
cm.
16.将三角尺绕着它的一条直角边旋转一周得到
体.
17.如图,在长方体ABCD﹣EFGH中,与面ADHE平行的面是
.
18.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子(添加所有符合要求的正方形,添加的正方形用阴影表示)
.
19.将下列几何体分类,柱体有:
(填序号).
20.如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有
种拼接方法.
三.解答题
21.已知一个长方体的长为1cm,宽为1cm,高为2cm,请求出:
(1)长方体有
条棱,
个面;
(2)长方体所有棱长的和;
(3)长方体的表面积.
22.如图,长方形的面积和圆的面积相等,已知点O为圆心,圆的半径是4厘米,求阴影部分的周长和面积.
23.将下列几何体与它的名称连接起来.
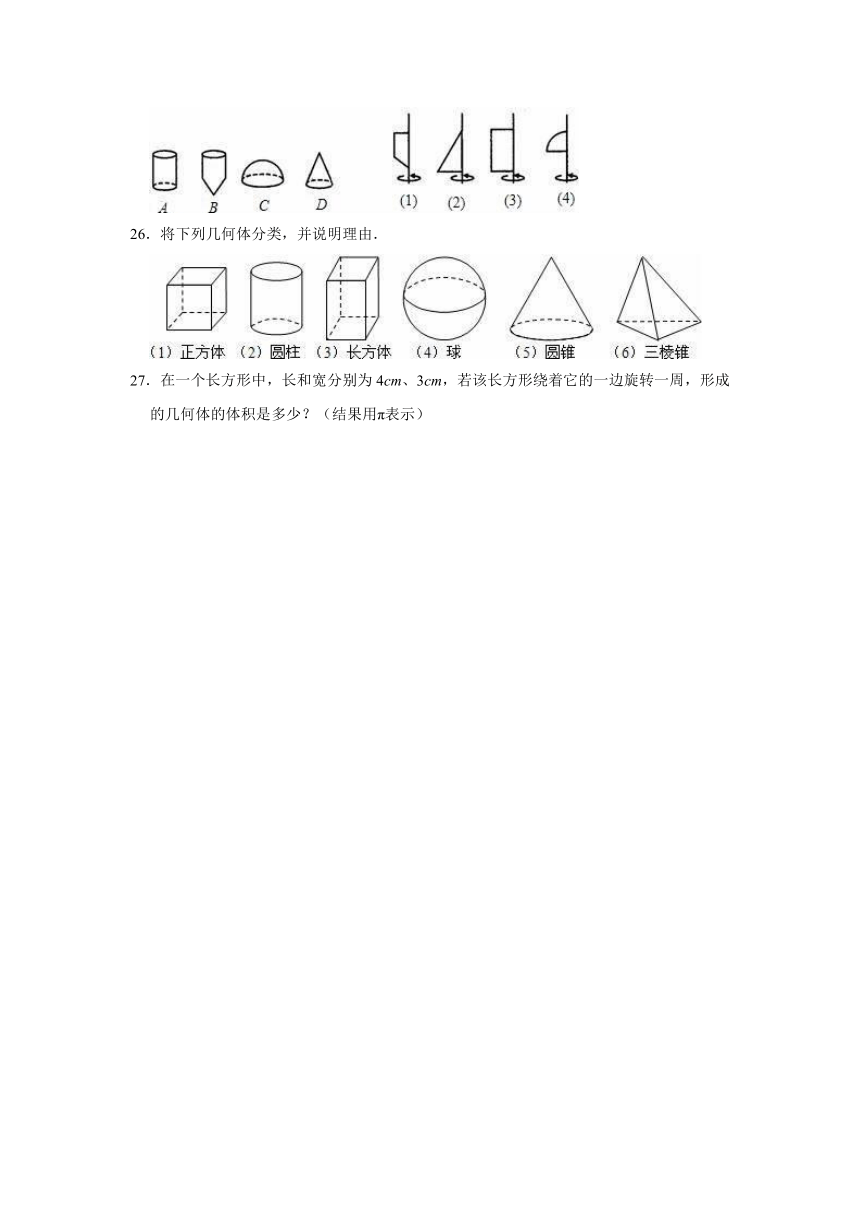
24.如图,上面是一些具体的物体,下面是一些立体图形,试找出与下面立体图形相类似的实物(用线连接).
25.用第一行的图形绕轴旋转一周,便得到第二行的几何体,用线连一连.
26.将下列几何体分类,并说明理由.
27.在一个长方形中,长和宽分别为4cm、3cm,若该长方形绕着它的一边旋转一周,形成的几何体的体积是多少?(结果用π表示)
参考答案与试题解析
一.选择题
1.解:A、圆柱由上下两个平面和侧面一个曲面组成;
B、圆锥由侧面一个曲面和底面一个平面组成;
C、球只有一个曲面组成;
D、正方体是由四个平面组成.
故选:C.
2.解:若按如图方法摆放,
则△ABC为等腰三角形,其高为AD,
则AB=0.8=,BD=0.4+=,
由勾股定理,得AD=≈0.65276,
∵0.8+4×0.65276=3.411>3.4,这种情况不可能,
这样有4个高<2.8+0.4+0.4<3.6,最后还剩下0.9×3.4还可以放4支.
这样,长放0.4+(4个<0.7)+0.4+0.8<4.4<4.5,
宽放4个0.8=3.2<3.4,共4+3+4+3+4+4=22支(如图).
故选:C.
3.解:∵三角形、正方形、长方形都是平面直线图形,圆是平面曲线图形,
∴平面上曲线图形只有圆,
故选:A.
4.解:在一个正方体的玻璃容器内装了一些水,把容器按不同方式倾斜,容器内水面的形状不可能是钝角三角形,
故选:B.
5.解:根据面动成体结合常见立体图形的形状得出只有A选项符合,
故选:A.
6.解:A、圆柱由矩形旋转可得,故此选项不合题意;
B、圆锥由直角三角形旋转可得,故此选项不合题意;
C、球由半圆旋转可得,故此选项不合题意;
D、六棱柱不是由一个平面图形通过旋转得到的,故此选项符合题意;
故选:D.
7.解:A、三棱锥有一个底面,三个侧面组成,共4个面.
B、三棱柱有二个底面,三个侧面组成,共5个面.
C、四棱锥有一个底面,四个侧面组成,共5个面.
D、四棱柱有二个底面,四个侧面组成,共6个面.
故有4个面的是三棱锥.
故选:A.
8.解:由原正方体的特征可知,含有4,6,8的数字的三个面一定相交于一点,而选项B、C、D中,经过折叠后与含有4,6,8的数字的三个面一定相交于一点不符.
故选:A.
9.解:如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,编号为1、2、3、4的小正方形中不能剪去的是4;
故选:D.
10.解:∵正方体的展开图,原正方体“4”的相对面上的数字为2,
∴原正方体“4”的相邻面上的数字分别为1,3,5,6,
∴原正方体“4”的相邻面上的数字之和是15,
故选:D.
二.填空题
11.解:一枚硬币在光滑的桌面上快速旋转形成一个球,这说明了面动成体,
故答案为:面动成体.
12.解:根据题意得:
第一层露出的表面积为:1×1×6﹣1×1=5;
第二层露出的表面积为:1×1×6×4﹣1×1×13=11;
第三层露出的表面积为:1×1×6×9﹣1×1×37=17.
所以红色部分的面积为:5+11+17=33.
故答案为:33.
13.解:由图可知,x,y的对面分别是8,2,则x,y所表示的数分别是﹣8,﹣2.
故x+y=﹣8+(﹣2)=﹣10.
故答案为:﹣10.
14.解:∵一个棱柱有16个顶点,
∴该棱柱是八棱柱,
∴这个棱柱有8个侧面,有24条棱.
故答案为:8,24.
15.解:直径为6cm的圆周长是:6πcm.
故答案为:6π.
16.解:将三角尺绕着它的一条直角边旋转一周得到圆锥体.
17.解:根据长方体的特征,相对的面的面积相等且平行,由此得:与面ADHE平行的面是面BCGF.
故答案为:面BCGF.
18.解:,
故答案为:.
19.解:柱体分为圆柱和棱柱,所以柱体有:(1)(2)(3).
故答案为:(1)(2)(3).
20.解:如图所示:
故小丽总共能有4种拼接方法.
故答案为:4.
三.解答题
21.解:(1)长方体有12条棱,6个面;
故答案为:12,6;
(2)(1+1+2)×4
=4×4
=16(cm).
故长方体所有棱长的和是16cm;
(3)(1×1+1×2+1×2)×2
=(1+2+2)×2
=5×2
=10(cm2).
故长方体的表面积是10cm2.
22.解:圆的面积:
3.14×42
=3.14×16
=50.24(平方厘米),
长方形的长:50.24÷4=12.56(厘米),
长方形的周长:(12.56+4)×2
=16.56×2
=33.12(厘米),
则阴影部分的周长:
33.12﹣4×2+3.14×4×2×=33.12﹣8+25.12×=25.12+6.28=31.4(厘米);
阴影部分的面积:
3.14×42×(1)
=3.14×16×=50.24×=37.68(平方厘米);
答:阴影部分的周长是31.4厘米,面积为37.68平方厘米.
23.解:如图所示:
24.解:埃及金字塔﹣﹣(2)
西瓜﹣﹣(3)
水杯﹣﹣(1)
房屋﹣﹣(5).
25.解:图(1)旋转一周形成一个圆柱与一个圆锥的组合体,即B;图(2)旋转一周形成圆锥,即D;图(3)旋转一周形成圆柱,即A;图(4)旋转一周形成半球,即C.
(1)─B,
(2)─D,
(3)─A,
(4)─C.
26.解:答案不唯一,如
(1)按平面分:正方体,长方体,三棱锥;
(2)按曲面分:圆柱,圆锥,球.
理由是:正方体的面是六个正方形组成,长方体的面是六个长方形组成,三棱锥的面是四个三角形组成,都是平面图形;而圆柱和圆锥的侧面都是曲面,球的整个面是曲面.
27.解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.
绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3.
故形成的几何体的体积是36πcm3或48πcm3.
基本的几何图形》单元测试卷
一.选择题
1.下面几何体中,全是由曲面围成的是( )
A.圆柱
B.圆锥
C.球
D.正方体
2.某同学用牙膏纸盒制作一个如图所示的笔筒,笔筒的筒底为长4.5厘米,宽3.4厘米的矩形.则该笔筒最多能放半径为0.4厘米的圆柱形铅笔( )
A.20支
B.21支
C.22支
D.25支
3.在下列图形中,是平面上曲线图形的有( )个
①三角形②正方形③长方形④圆.
A.1
B.2
C.3
D.4
4.在一个正方体的玻璃容器内装了一些水,把容器按不同方式倾斜,容器内水面的形状不可能是以下哪些图形( )
A.锐角三角形
B.钝角三角形
C.等腰梯形
D.五边形
5.将下面四个图形绕着虚线旋转一周,能够得到如图所说的
立体图形的是( )
A.
B.
C.
D.
6.下面几何体中,不能由一个平面图形通过旋转得到的是( )
A.
B.
C.
D.
7.下列的立体图形中,有4个面的是( )
A.三棱锥
B.三棱柱
C.四棱锥
D.四棱柱
8.如果有一个正方体,它的展开图可能是下列四个展开图中的( )
A.
B.
C.
D.
9.将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,下列编号为1,2,3,4的小正方形中不能剪去的是( )
A.1
B.2
C.3
D.4
10.如图所示是正方体的展开图,原正方体“4”的相邻面上的数字之和是( )
A.2
B.12
C.14
D.15
二.填空题
11.雨点从高空落下形成的轨迹说明了点动成线,那么一枚硬币在光滑的桌面上快速旋转形成一个球,这说明了
.
12.李强同学用棱长为1的正方体在桌面上堆成如图所示的图形,然后把露出的表面都染成红色,则表面被他染成红色的面积为
.
13.一个正方体的相对的表面上所标的两个数,都是互为相反的两个数,如图是这个正方形的表面展开图,则x+y=
.
14.一个棱柱有16个顶点,则这个棱柱有
个侧面,有
条棱.
15.直径为6cm的圆周长是
cm.
16.将三角尺绕着它的一条直角边旋转一周得到
体.
17.如图,在长方体ABCD﹣EFGH中,与面ADHE平行的面是
.
18.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在图中的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子(添加所有符合要求的正方形,添加的正方形用阴影表示)
.
19.将下列几何体分类,柱体有:
(填序号).
20.如图,5个边长相等的小正方形拼成一个平面图形,小丽手中还有一个同样的小正方形,她想将它与图中的平面图形拼接在一起,从而可以构成一个正方体的平面展开图,则小丽总共能有
种拼接方法.
三.解答题
21.已知一个长方体的长为1cm,宽为1cm,高为2cm,请求出:
(1)长方体有
条棱,
个面;
(2)长方体所有棱长的和;
(3)长方体的表面积.
22.如图,长方形的面积和圆的面积相等,已知点O为圆心,圆的半径是4厘米,求阴影部分的周长和面积.
23.将下列几何体与它的名称连接起来.
24.如图,上面是一些具体的物体,下面是一些立体图形,试找出与下面立体图形相类似的实物(用线连接).
25.用第一行的图形绕轴旋转一周,便得到第二行的几何体,用线连一连.
26.将下列几何体分类,并说明理由.
27.在一个长方形中,长和宽分别为4cm、3cm,若该长方形绕着它的一边旋转一周,形成的几何体的体积是多少?(结果用π表示)
参考答案与试题解析
一.选择题
1.解:A、圆柱由上下两个平面和侧面一个曲面组成;
B、圆锥由侧面一个曲面和底面一个平面组成;
C、球只有一个曲面组成;
D、正方体是由四个平面组成.
故选:C.
2.解:若按如图方法摆放,
则△ABC为等腰三角形,其高为AD,
则AB=0.8=,BD=0.4+=,
由勾股定理,得AD=≈0.65276,
∵0.8+4×0.65276=3.411>3.4,这种情况不可能,
这样有4个高<2.8+0.4+0.4<3.6,最后还剩下0.9×3.4还可以放4支.
这样,长放0.4+(4个<0.7)+0.4+0.8<4.4<4.5,
宽放4个0.8=3.2<3.4,共4+3+4+3+4+4=22支(如图).
故选:C.
3.解:∵三角形、正方形、长方形都是平面直线图形,圆是平面曲线图形,
∴平面上曲线图形只有圆,
故选:A.
4.解:在一个正方体的玻璃容器内装了一些水,把容器按不同方式倾斜,容器内水面的形状不可能是钝角三角形,
故选:B.
5.解:根据面动成体结合常见立体图形的形状得出只有A选项符合,
故选:A.
6.解:A、圆柱由矩形旋转可得,故此选项不合题意;
B、圆锥由直角三角形旋转可得,故此选项不合题意;
C、球由半圆旋转可得,故此选项不合题意;
D、六棱柱不是由一个平面图形通过旋转得到的,故此选项符合题意;
故选:D.
7.解:A、三棱锥有一个底面,三个侧面组成,共4个面.
B、三棱柱有二个底面,三个侧面组成,共5个面.
C、四棱锥有一个底面,四个侧面组成,共5个面.
D、四棱柱有二个底面,四个侧面组成,共6个面.
故有4个面的是三棱锥.
故选:A.
8.解:由原正方体的特征可知,含有4,6,8的数字的三个面一定相交于一点,而选项B、C、D中,经过折叠后与含有4,6,8的数字的三个面一定相交于一点不符.
故选:A.
9.解:如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,编号为1、2、3、4的小正方形中不能剪去的是4;
故选:D.
10.解:∵正方体的展开图,原正方体“4”的相对面上的数字为2,
∴原正方体“4”的相邻面上的数字分别为1,3,5,6,
∴原正方体“4”的相邻面上的数字之和是15,
故选:D.
二.填空题
11.解:一枚硬币在光滑的桌面上快速旋转形成一个球,这说明了面动成体,
故答案为:面动成体.
12.解:根据题意得:
第一层露出的表面积为:1×1×6﹣1×1=5;
第二层露出的表面积为:1×1×6×4﹣1×1×13=11;
第三层露出的表面积为:1×1×6×9﹣1×1×37=17.
所以红色部分的面积为:5+11+17=33.
故答案为:33.
13.解:由图可知,x,y的对面分别是8,2,则x,y所表示的数分别是﹣8,﹣2.
故x+y=﹣8+(﹣2)=﹣10.
故答案为:﹣10.
14.解:∵一个棱柱有16个顶点,
∴该棱柱是八棱柱,
∴这个棱柱有8个侧面,有24条棱.
故答案为:8,24.
15.解:直径为6cm的圆周长是:6πcm.
故答案为:6π.
16.解:将三角尺绕着它的一条直角边旋转一周得到圆锥体.
17.解:根据长方体的特征,相对的面的面积相等且平行,由此得:与面ADHE平行的面是面BCGF.
故答案为:面BCGF.
18.解:,
故答案为:.
19.解:柱体分为圆柱和棱柱,所以柱体有:(1)(2)(3).
故答案为:(1)(2)(3).
20.解:如图所示:
故小丽总共能有4种拼接方法.
故答案为:4.
三.解答题
21.解:(1)长方体有12条棱,6个面;
故答案为:12,6;
(2)(1+1+2)×4
=4×4
=16(cm).
故长方体所有棱长的和是16cm;
(3)(1×1+1×2+1×2)×2
=(1+2+2)×2
=5×2
=10(cm2).
故长方体的表面积是10cm2.
22.解:圆的面积:
3.14×42
=3.14×16
=50.24(平方厘米),
长方形的长:50.24÷4=12.56(厘米),
长方形的周长:(12.56+4)×2
=16.56×2
=33.12(厘米),
则阴影部分的周长:
33.12﹣4×2+3.14×4×2×=33.12﹣8+25.12×=25.12+6.28=31.4(厘米);
阴影部分的面积:
3.14×42×(1)
=3.14×16×=50.24×=37.68(平方厘米);
答:阴影部分的周长是31.4厘米,面积为37.68平方厘米.
23.解:如图所示:
24.解:埃及金字塔﹣﹣(2)
西瓜﹣﹣(3)
水杯﹣﹣(1)
房屋﹣﹣(5).
25.解:图(1)旋转一周形成一个圆柱与一个圆锥的组合体,即B;图(2)旋转一周形成圆锥,即D;图(3)旋转一周形成圆柱,即A;图(4)旋转一周形成半球,即C.
(1)─B,
(2)─D,
(3)─A,
(4)─C.
26.解:答案不唯一,如
(1)按平面分:正方体,长方体,三棱锥;
(2)按曲面分:圆柱,圆锥,球.
理由是:正方体的面是六个正方形组成,长方体的面是六个长方形组成,三棱锥的面是四个三角形组成,都是平面图形;而圆柱和圆锥的侧面都是曲面,球的整个面是曲面.
27.解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.
绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3.
故形成的几何体的体积是36πcm3或48πcm3.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
