4.4.2 与坡度、坡角有关的实际问题 课件(共20张PPT)
文档属性
| 名称 | 4.4.2 与坡度、坡角有关的实际问题 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 00:00:00 | ||
图片预览








文档简介
4.4.2 与坡度、坡角有关的实际问题
湘教版·九年级数学上册
新课导入
如图所示,斜坡AB和斜坡A1B1,哪一个倾斜程度比较大?
显然,斜坡A1B1的倾斜程度比较大,说明∠A1>∠A.
从图形可以看出 ,
即tan A1>tan A.
(1)
(2)
图(1)和(2)中,哪个山坡比较陡?
很明显,(2)中的山坡比较陡.
探究新知
如图所示,从山脚到山顶有两条路AB与BD,问哪条路比较陡?
观 察
右边的路BD陡些.
如何用数量来刻画哪条路陡呢?
如图所示,从山坡脚下点A上坡走到点B时,升高的高度h(即线段BC的长度)与水平前进的距离l(即线段AC的长度)的比叫作坡度,用字母i表示,即
(坡度通常写成1∶m的形式).
坡角:山坡与地平面的夹角α叫坡角.
坡度越大,山坡越陡.
∠BAC叫作坡角.
例2:如图,一山坡的坡度为 i = 1∶2 . 小刚从山脚A出发, 沿山坡向上走了240m 到达点C. 这座山坡的坡角是多少度?小刚上升了多少米?(角度精确到0.01°,长度精确到0.1m)
i=1∶2
分析:在直角三角形ABC中,已知了坡度即角α的正切可求出坡角α,然后用α的正弦求出对边BC的长.
解:用α表示坡角的大小, 由题意可得
因此α ≈26.57°.
如图,在Rt△ABC中,
∠B =90°,∠A = 26.57°,AC=240m ,
因此
从而BC=240×sin 26.57°≈ 107.3(m).
答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m.
你还可以用其他方法求出BC吗?
练习
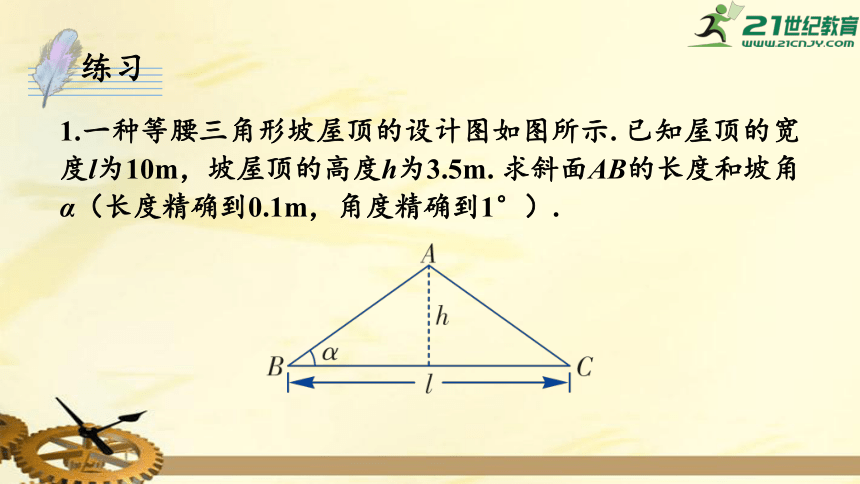
1.一种等腰三角形坡屋顶的设计图如图所示. 已知屋顶的宽度l为10m,坡屋顶的高度h为3.5m. 求斜面AB的长度和坡角α(长度精确到0.1m,角度精确到1°).
解:设CB中点为D ,则由图可知
D
AD⊥BC.
在Rt△ABD中,
AD=h=3.5m,
由勾股定理得
又
∴α ≈ 35°
2.如图,在山坡上种树,要求株距(相邻两树间的水平距离)是5.5m,测得斜坡的倾斜角是24°,求斜坡上相邻两树的坡面距离是多少(精确到0.1m).
分析:将实际问题转化为数学问题画出图形.
解:在Rt△ABC中,∠C=90°,AC=5.5,∠A=24°,求AB.
在Rt△ABC中,
∴AB=
答:斜坡上相邻两树间的坡面距离约是6.0m.
3.如图水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡面角α,坝底宽AD和斜坡AB的长(精确到0.1m).
解:作BE⊥AD,CF⊥AD,在Rt△ABE和Rt△CDF中,
∴AE=3·BE=3×23=69(m).
FD=2.5·CF=2.5×23=57.5(m).
∴AD=AE+EF+FD=69+6+57.5=132.5(m).
∵斜坡AB的坡度
∴α ≈ 18°26′.
∵
∴
4.庞亮和李强相约周六去登山,庞亮从北坡山脚C处出发,以24米/分钟的速度攀登,同时,李强从南坡山脚B处出发.如图,已知小山北坡的坡度i=1∶ ,山坡长为240米,南坡的坡角是45°.问李强以什么速度攀登才能和庞亮同时到达山顶A?(将山路AB、AC看成线段,结果保留根号)
解:过点A作AD⊥BC于点D,
在Rt△ADC中,由i=1∶ 得
∴∠C=30°.
∴
在Rt△ABD中,∠B=45°,
∴
答:李强以12 米/分钟的速度攀登才能和庞亮同时到达山顶A.
课堂小结
坡面的垂直高度h和水平宽度l的比叫坡度(或叫坡比)用字母表示为:
(坡度通常写成1∶m的形式).
坡度越大,山坡越陡.
坡角:山坡与地平面的夹角α叫坡角.
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
湘教版·九年级数学上册
新课导入
如图所示,斜坡AB和斜坡A1B1,哪一个倾斜程度比较大?
显然,斜坡A1B1的倾斜程度比较大,说明∠A1>∠A.
从图形可以看出 ,
即tan A1>tan A.
(1)
(2)
图(1)和(2)中,哪个山坡比较陡?
很明显,(2)中的山坡比较陡.
探究新知
如图所示,从山脚到山顶有两条路AB与BD,问哪条路比较陡?
观 察
右边的路BD陡些.
如何用数量来刻画哪条路陡呢?
如图所示,从山坡脚下点A上坡走到点B时,升高的高度h(即线段BC的长度)与水平前进的距离l(即线段AC的长度)的比叫作坡度,用字母i表示,即
(坡度通常写成1∶m的形式).
坡角:山坡与地平面的夹角α叫坡角.
坡度越大,山坡越陡.
∠BAC叫作坡角.
例2:如图,一山坡的坡度为 i = 1∶2 . 小刚从山脚A出发, 沿山坡向上走了240m 到达点C. 这座山坡的坡角是多少度?小刚上升了多少米?(角度精确到0.01°,长度精确到0.1m)
i=1∶2
分析:在直角三角形ABC中,已知了坡度即角α的正切可求出坡角α,然后用α的正弦求出对边BC的长.
解:用α表示坡角的大小, 由题意可得
因此α ≈26.57°.
如图,在Rt△ABC中,
∠B =90°,∠A = 26.57°,AC=240m ,
因此
从而BC=240×sin 26.57°≈ 107.3(m).
答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m.
你还可以用其他方法求出BC吗?
练习
1.一种等腰三角形坡屋顶的设计图如图所示. 已知屋顶的宽度l为10m,坡屋顶的高度h为3.5m. 求斜面AB的长度和坡角α(长度精确到0.1m,角度精确到1°).
解:设CB中点为D ,则由图可知
D
AD⊥BC.
在Rt△ABD中,
AD=h=3.5m,
由勾股定理得
又
∴α ≈ 35°
2.如图,在山坡上种树,要求株距(相邻两树间的水平距离)是5.5m,测得斜坡的倾斜角是24°,求斜坡上相邻两树的坡面距离是多少(精确到0.1m).
分析:将实际问题转化为数学问题画出图形.
解:在Rt△ABC中,∠C=90°,AC=5.5,∠A=24°,求AB.
在Rt△ABC中,
∴AB=
答:斜坡上相邻两树间的坡面距离约是6.0m.
3.如图水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡面角α,坝底宽AD和斜坡AB的长(精确到0.1m).
解:作BE⊥AD,CF⊥AD,在Rt△ABE和Rt△CDF中,
∴AE=3·BE=3×23=69(m).
FD=2.5·CF=2.5×23=57.5(m).
∴AD=AE+EF+FD=69+6+57.5=132.5(m).
∵斜坡AB的坡度
∴α ≈ 18°26′.
∵
∴
4.庞亮和李强相约周六去登山,庞亮从北坡山脚C处出发,以24米/分钟的速度攀登,同时,李强从南坡山脚B处出发.如图,已知小山北坡的坡度i=1∶ ,山坡长为240米,南坡的坡角是45°.问李强以什么速度攀登才能和庞亮同时到达山顶A?(将山路AB、AC看成线段,结果保留根号)
解:过点A作AD⊥BC于点D,
在Rt△ADC中,由i=1∶ 得
∴∠C=30°.
∴
在Rt△ABD中,∠B=45°,
∴
答:李强以12 米/分钟的速度攀登才能和庞亮同时到达山顶A.
课堂小结
坡面的垂直高度h和水平宽度l的比叫坡度(或叫坡比)用字母表示为:
(坡度通常写成1∶m的形式).
坡度越大,山坡越陡.
坡角:山坡与地平面的夹角α叫坡角.
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
