4.4 解直角三角形的应用 习题课件(共20张PPT)
文档属性
| 名称 | 4.4 解直角三角形的应用 习题课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 00:00:00 | ||
图片预览








文档简介
湘教版·九年级数学上册
1.如图,有一段斜坡BC长为10m,坡角∠CBD=12°,为方便残疾人的轮椅通行,现准备把坡角降为5°.
(1)求坡高CD(结果精确到0.1m);
(2)求斜坡新起点A与原起点B的距离(结果精确到0.1m).
解:(1)∵
∴CD=BC·sin∠CBD=10×sin12°≈2.1 m.
(2)∵
∴
同理可得BD≈9.9m
∴AB=AD-BD=14.1m
2.如图所示,渔船在A处看到灯塔C在北偏东60°方向上,渔船向正东方向航行了12km到达B处,在B处看到灯塔C在正北方向上,这时渔船与灯塔C的距离是多少?
解:∵
∴
3.图(1)是一间安装有壁挂式空调的卧室的一部分,图(2)是该空调挂机的侧面示意图. 已知空调挂机底部BC垂直于墙面CD,且当导风板所在直线AE与竖直线AB的夹角α为40°时,空调风刚好吹到床的外边沿E处.若AB=0.02m,BC=0.2m,床铺长DE=2.3m,求空调挂机底部位置距离床的高度CD(结果精确到0.1m).
解:设射线AB交DE于点F,由题意得,DF=0.2m,CD=BF,
F
∵EF=DE-DF=2.3-0.2=2.1(m),
∴
∴BF≈2.5(m),
∴CD=BF≈2.5(m),
∴空调挂机底部位置距离床的高度CD约为2.5m.
4.如图所示,某同学站在距离圣诞树3m的位置C处.已知他的目高CD为1.4m.若他测得树顶的仰角为30°,求该圣诞树的高度(结果精确到0.1m).
解:如图所示,由题意得DE=BC=3m,BE=CD=1.4m,
在Rt△ADE中,tan∠ADE=
∴AE=3·tan30°≈1.7(m),
∴AB=AE+EB≈1.7+1.4=3.1(m).
∴该圣诞树的高度约为3.1m.
E
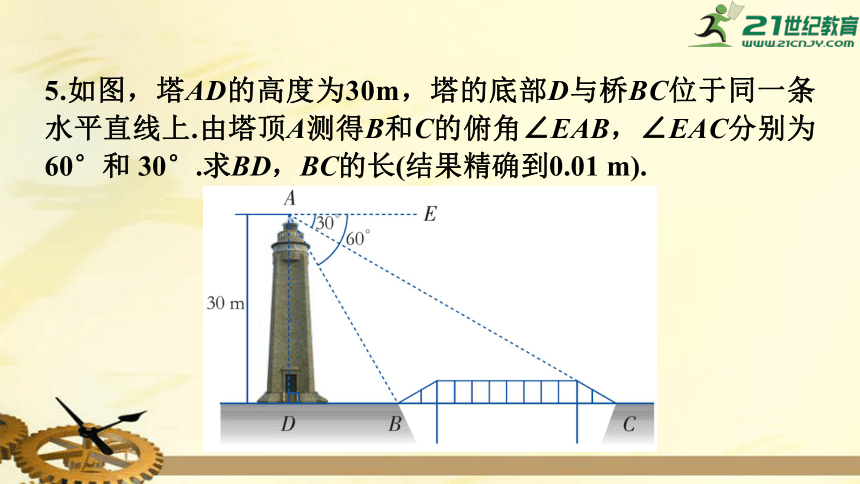
5.如图,塔AD的高度为30m,塔的底部D与桥BC位于同一条水平直线上.由塔顶A测得B和C的俯角∠EAB,∠EAC分别为60°和 30°.求BD,BC的长(结果精确到0.01 m).
解:由题意得∠BAD=90°-60°=30°,
∠CAD=90°-30°=60°,
在Rt△BAD中,tan∠BAD =
∴BD=30·tan30°= (m)≈17.32(m),
同理可得CD= (m),
∴BC=CD-BD
6.如图(a),A,B和C是三个小岛.一艘船由A处出发向正东方向航行4km到达B处,然后向正北方向航行3km到达C处.
(1)求由A测得C的方位角的大小(结果精确到1°).
解:在Rt△ABC中,
∴∠ACB≈53°,
∴由A测得C的方位角的大小约为53°.
(2)如图(b),直升机由C飞往A,其飞行高度一直保持在海平面以上的h km.当直升机飞到P处时,由Р测得C和A的俯角分别是48°和65°.已知A,C,P和海平面上一点M都在同一个平面上,且M位于P的正下方,求h(结果精确到0.1km).
解:由题意得,∠PAM=65°,∠PCM=48°,
在Rt△ABC中,∵AB=4 km,BC=3 km,
∴
在Rt△APM中,∵tan∠PAM=
∴
在Rt△PCM中,∵tan∠PCM=
∴
∵AC=AM+CM,即5=0.5h+0.9h,
∴h≈3.6(km).
7.如图,MN表示水平地面,由地面上A处测得山上B处的仰角是25°,由山顶C处测得B处的俯角是40°.若AB∶BC=2∶3,求由A处测得C处的仰角(结果精确到0.1°).
解:如图,过点B作BD⊥MN于点D,并反向延长BD交CE于点E,则BE⊥CE,过点C作CF⊥MN于点F,则CF=DE,CE=FD,
D
E
F
∵AB∶BC=2∶3,
∴设AB=2k,则BC=3k,
在Rt△BAD中,
∴AD=2k·cos25°≈1.8k,
D
E
F
∵
∴BD=2k·sin25°≈0.8k,
在Rt△BCE中,
∴CE=3k·cos40°≈2.3k,
∴DF=CE≈2.3k,
∵
∴BE=3k·sin40°≈1.9k,
D
E
F
∴DE=BD+BE≈0.8k+1.9k=2.7k,AF=AD+DF≈1.8k+2.3k=4.1k,
∴CF≈2.7k,
在Rt△CAF中,
∴∠CAF≈33.4°,
∴由A处测得C处的仰角约为33.4°.
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
1.如图,有一段斜坡BC长为10m,坡角∠CBD=12°,为方便残疾人的轮椅通行,现准备把坡角降为5°.
(1)求坡高CD(结果精确到0.1m);
(2)求斜坡新起点A与原起点B的距离(结果精确到0.1m).
解:(1)∵
∴CD=BC·sin∠CBD=10×sin12°≈2.1 m.
(2)∵
∴
同理可得BD≈9.9m
∴AB=AD-BD=14.1m
2.如图所示,渔船在A处看到灯塔C在北偏东60°方向上,渔船向正东方向航行了12km到达B处,在B处看到灯塔C在正北方向上,这时渔船与灯塔C的距离是多少?
解:∵
∴
3.图(1)是一间安装有壁挂式空调的卧室的一部分,图(2)是该空调挂机的侧面示意图. 已知空调挂机底部BC垂直于墙面CD,且当导风板所在直线AE与竖直线AB的夹角α为40°时,空调风刚好吹到床的外边沿E处.若AB=0.02m,BC=0.2m,床铺长DE=2.3m,求空调挂机底部位置距离床的高度CD(结果精确到0.1m).
解:设射线AB交DE于点F,由题意得,DF=0.2m,CD=BF,
F
∵EF=DE-DF=2.3-0.2=2.1(m),
∴
∴BF≈2.5(m),
∴CD=BF≈2.5(m),
∴空调挂机底部位置距离床的高度CD约为2.5m.
4.如图所示,某同学站在距离圣诞树3m的位置C处.已知他的目高CD为1.4m.若他测得树顶的仰角为30°,求该圣诞树的高度(结果精确到0.1m).
解:如图所示,由题意得DE=BC=3m,BE=CD=1.4m,
在Rt△ADE中,tan∠ADE=
∴AE=3·tan30°≈1.7(m),
∴AB=AE+EB≈1.7+1.4=3.1(m).
∴该圣诞树的高度约为3.1m.
E
5.如图,塔AD的高度为30m,塔的底部D与桥BC位于同一条水平直线上.由塔顶A测得B和C的俯角∠EAB,∠EAC分别为60°和 30°.求BD,BC的长(结果精确到0.01 m).
解:由题意得∠BAD=90°-60°=30°,
∠CAD=90°-30°=60°,
在Rt△BAD中,tan∠BAD =
∴BD=30·tan30°= (m)≈17.32(m),
同理可得CD= (m),
∴BC=CD-BD
6.如图(a),A,B和C是三个小岛.一艘船由A处出发向正东方向航行4km到达B处,然后向正北方向航行3km到达C处.
(1)求由A测得C的方位角的大小(结果精确到1°).
解:在Rt△ABC中,
∴∠ACB≈53°,
∴由A测得C的方位角的大小约为53°.
(2)如图(b),直升机由C飞往A,其飞行高度一直保持在海平面以上的h km.当直升机飞到P处时,由Р测得C和A的俯角分别是48°和65°.已知A,C,P和海平面上一点M都在同一个平面上,且M位于P的正下方,求h(结果精确到0.1km).
解:由题意得,∠PAM=65°,∠PCM=48°,
在Rt△ABC中,∵AB=4 km,BC=3 km,
∴
在Rt△APM中,∵tan∠PAM=
∴
在Rt△PCM中,∵tan∠PCM=
∴
∵AC=AM+CM,即5=0.5h+0.9h,
∴h≈3.6(km).
7.如图,MN表示水平地面,由地面上A处测得山上B处的仰角是25°,由山顶C处测得B处的俯角是40°.若AB∶BC=2∶3,求由A处测得C处的仰角(结果精确到0.1°).
解:如图,过点B作BD⊥MN于点D,并反向延长BD交CE于点E,则BE⊥CE,过点C作CF⊥MN于点F,则CF=DE,CE=FD,
D
E
F
∵AB∶BC=2∶3,
∴设AB=2k,则BC=3k,
在Rt△BAD中,
∴AD=2k·cos25°≈1.8k,
D
E
F
∵
∴BD=2k·sin25°≈0.8k,
在Rt△BCE中,
∴CE=3k·cos40°≈2.3k,
∴DF=CE≈2.3k,
∵
∴BE=3k·sin40°≈1.9k,
D
E
F
∴DE=BD+BE≈0.8k+1.9k=2.7k,AF=AD+DF≈1.8k+2.3k=4.1k,
∴CF≈2.7k,
在Rt△CAF中,
∴∠CAF≈33.4°,
∴由A处测得C处的仰角约为33.4°.
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
