第四章 锐角三角函数 章末复习 课件(共34张PPT)
文档属性
| 名称 | 第四章 锐角三角函数 章末复习 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 21:34:09 | ||
图片预览








文档简介
第四章 章末复习
湘教版·九年级数学上册
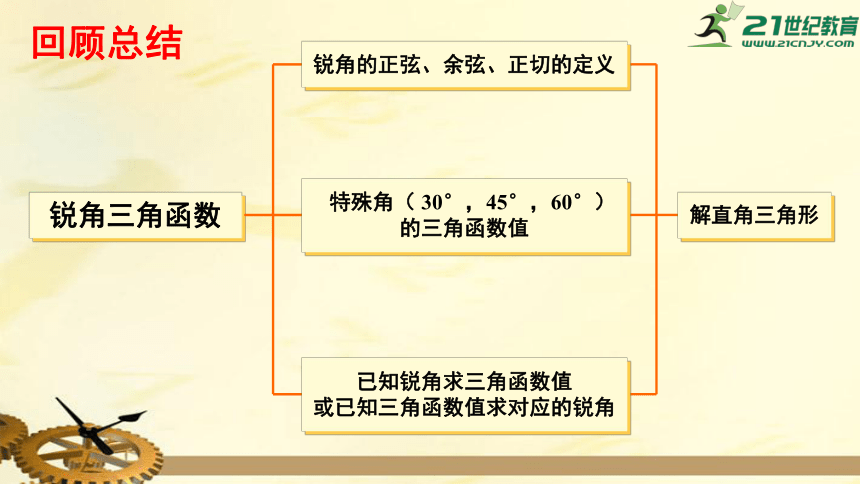
回顾总结
锐角三角函数
锐角的正弦、余弦、正切的定义
特殊角( 30°,45°,60°)
的三角函数值
已知锐角求三角函数值
或已知三角函数值求对应的锐角
解直角三角形
正弦
如图,在直角三角形中,我们把锐角α的对边与斜边的比叫作角α的正弦,记作sinα,即
余弦
如图,在直角三角形中,我们把锐角α的邻边与斜边的比叫作角α的余弦,记作cosα,即
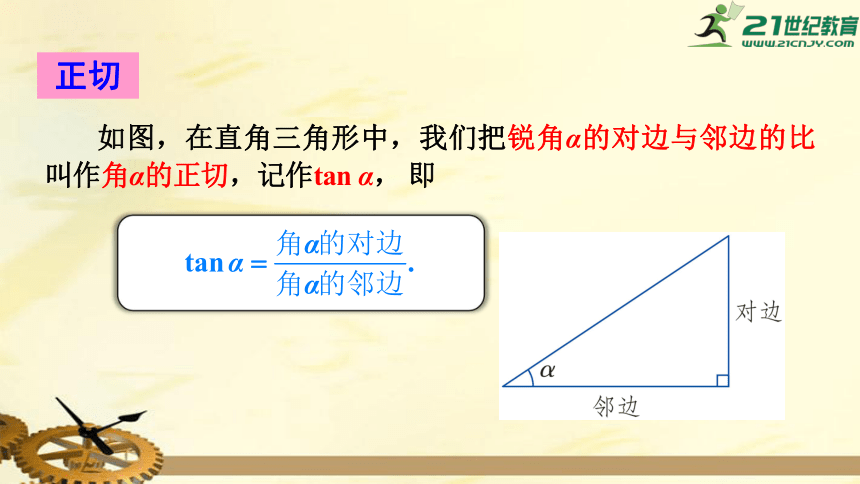
正切
如图,在直角三角形中,我们把锐角α的对边与邻边的比叫作角α的正切,记作tan α, 即
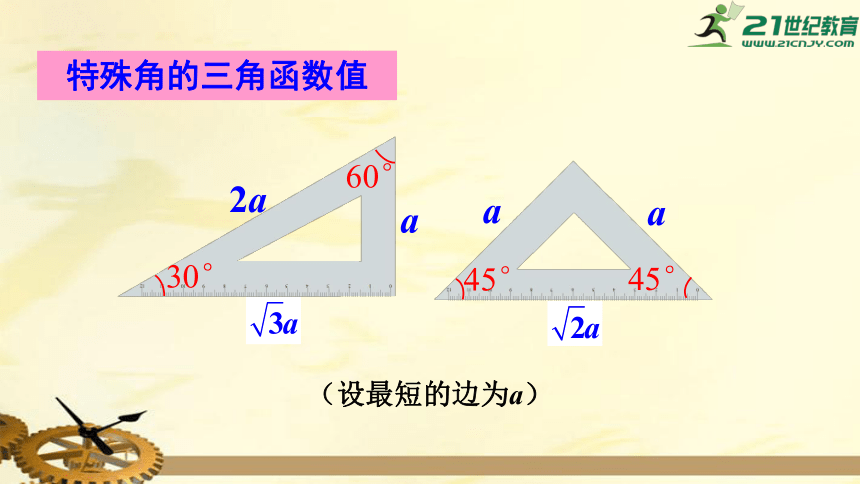
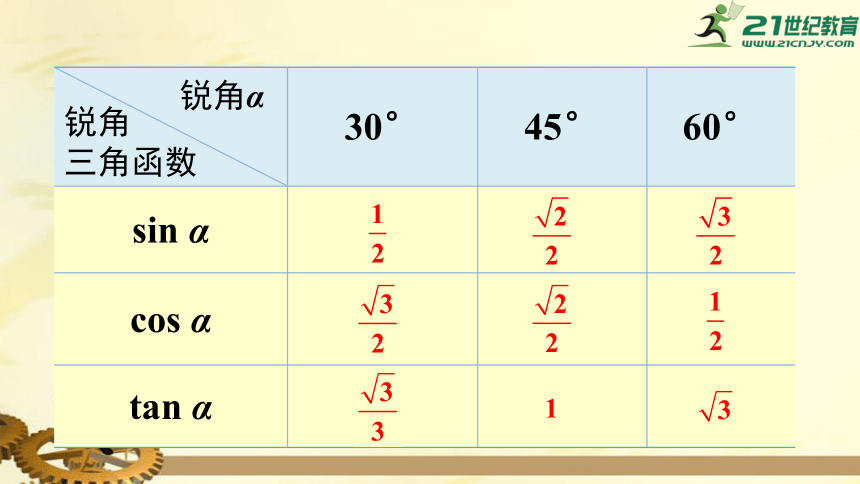
特殊角的三角函数值
a
2a
a
a
(设最短的边为a)
30°
60°
45°
45°
30°
45°
60°
sin α
cos α
tan α
锐角α
锐角
三角函数
解直角三角形的依据
(1)三边之间的关系:
(2)两锐角之间的关系:
a2+b2=c2(勾股定理)
∠A+∠B=90°
(3)边角之间的关系:
利用解直角三角形的知识解决实际问题的一般步骤
1.将实际问题抽象为数学问题;
2.根据问题中的条件,适当选用锐角三角函数等解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
注意
1.在直角三角形中,任一锐角的三角函数只与角的大小有关,而与直角三角形的大小无关.
2.在直角三角形中,已知一条边和一个角,或已知两条边,就可以求出其他的边和角.
3.有些关于图形的实际问题,我们可以结和已知条件,恰当地构造出直角三角形,画出图形,将实际问题转化为解直角三角形的问题.
课堂练习
解:在Rt△ABC中,∠C=90°,AB=12cm,BC=10cm,
∴
(1)解:1-2sin230°
(2)解:sin45°cos30°-cos45°sin30°
(3)解:
(4)解:
解:由tanα=0.625,α是锐角,得α ≈ 32°,
∴sinα=sin32°≈0.5299,
∴cosα=cos32°≈0.8480.
解:(1)sin3°15′≈0.0567,
cos3°15′≈0.9984,
tan3°15′≈0.0568.
(2)sin68°6′≈0.9278,
cos68°6′≈0.3730,
tan68°6′≈2.4876.
解:(1) α ≈ 19°. (2) α ≈ 44°. (3) α ≈ 16°.
解:∠B=180°-∠A-∠C=180°-30°-90°=60°,
∵
∴a=12·sin30°=
∵
∴b=12·cos30°=
解:如图,设AC,BD交于点O,
∵四边形ABCD是菱形,
∴AO=
AC⊥BD,
∴AB=
∵
∴∠ABC=2∠ABO≈2×53°=106°,
∴菱形的边长为3cm,∠DAB≈74°,
∠ABC≈106°.
∴∠OAB≈37°,
∴∠DAB≈37°×2=74°,
∴∠ABO≈90°-37°=53°.
解:(1)在Rt△CDE中,
∴
解:(2)设OD=x cm,则OB=x cm,在Rt△AOC中,
解得x = ,即OD的长度为 cm.
解:在Rt△END中,
∴ND=
在Rt△EMD中,
∴MD=
∵MN=MD-ND=25,
∴
解得ED ≈ 24.63(m),
∴点E到地面的距离ED约为24.63m.
解:在Rt△ABC中,
∴AB=d1·tan40°=4×tan40°≈3.356(m),
在Rt△ABD中,
∴d2=
∴DC=d2-d1≈4.619-4=0.619≈0.62(m).
∴楼梯占用地面增加的长度DC约为0.62m.
解:如图,连接OR,由题意得∠BOR=90°,
∠ARO=30°,∠BRO=45°,∴OB=OR.
∵
∴OA=4·sin30°=
又∵
∴
∴AB=OB-OA=OR-OA≈3.464-2=1.464(km).
∴火箭从A到B处的平均速度为1.464÷5=0.2928(km/s)≈293m/s.
解:如图,∵
∴∠A≈40°,∴∠B=90°-∠A≈50°.
∵AC2=AD2+CD2,
∴AC=
∵
∴BC=AC·tan A≈6.0×tan40°≈5.0(cm).
∵
∴AB=
解:由题意得BD=400-124=276(m),CB2=1100-400=700(m),
∠BAA2=30°,∠CBB2=45°.
在Rt△ABD中,sin∠BAD=sin30°=
∴AB=2BD=2×276=552(m).
在Rt△BCB2中,sin∠CBB2=sin45°=
∴BC=
∴AB+BC≈552+989.95≈1542(m).
答:钢缆AB和BC的总长度约为1542 m.
D
解:过C作CD⊥AB于D.
在Rt△CAD中,sin A=
∴CD=b·sin A.
∴
即
证明:由(1)可知
同理
∴
∴bsin A=asin B,
∴
解:由(2)可知
∴
即
∴
∴∠B=60°,
又∵BD=8,在Rt△BCD中,BC=2BD=16,
∴
在Rt△ADC中,AD= ,
∴AB=AD+BD=2+8=10.
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
湘教版·九年级数学上册
回顾总结
锐角三角函数
锐角的正弦、余弦、正切的定义
特殊角( 30°,45°,60°)
的三角函数值
已知锐角求三角函数值
或已知三角函数值求对应的锐角
解直角三角形
正弦
如图,在直角三角形中,我们把锐角α的对边与斜边的比叫作角α的正弦,记作sinα,即
余弦
如图,在直角三角形中,我们把锐角α的邻边与斜边的比叫作角α的余弦,记作cosα,即
正切
如图,在直角三角形中,我们把锐角α的对边与邻边的比叫作角α的正切,记作tan α, 即
特殊角的三角函数值
a
2a
a
a
(设最短的边为a)
30°
60°
45°
45°
30°
45°
60°
sin α
cos α
tan α
锐角α
锐角
三角函数
解直角三角形的依据
(1)三边之间的关系:
(2)两锐角之间的关系:
a2+b2=c2(勾股定理)
∠A+∠B=90°
(3)边角之间的关系:
利用解直角三角形的知识解决实际问题的一般步骤
1.将实际问题抽象为数学问题;
2.根据问题中的条件,适当选用锐角三角函数等解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
注意
1.在直角三角形中,任一锐角的三角函数只与角的大小有关,而与直角三角形的大小无关.
2.在直角三角形中,已知一条边和一个角,或已知两条边,就可以求出其他的边和角.
3.有些关于图形的实际问题,我们可以结和已知条件,恰当地构造出直角三角形,画出图形,将实际问题转化为解直角三角形的问题.
课堂练习
解:在Rt△ABC中,∠C=90°,AB=12cm,BC=10cm,
∴
(1)解:1-2sin230°
(2)解:sin45°cos30°-cos45°sin30°
(3)解:
(4)解:
解:由tanα=0.625,α是锐角,得α ≈ 32°,
∴sinα=sin32°≈0.5299,
∴cosα=cos32°≈0.8480.
解:(1)sin3°15′≈0.0567,
cos3°15′≈0.9984,
tan3°15′≈0.0568.
(2)sin68°6′≈0.9278,
cos68°6′≈0.3730,
tan68°6′≈2.4876.
解:(1) α ≈ 19°. (2) α ≈ 44°. (3) α ≈ 16°.
解:∠B=180°-∠A-∠C=180°-30°-90°=60°,
∵
∴a=12·sin30°=
∵
∴b=12·cos30°=
解:如图,设AC,BD交于点O,
∵四边形ABCD是菱形,
∴AO=
AC⊥BD,
∴AB=
∵
∴∠ABC=2∠ABO≈2×53°=106°,
∴菱形的边长为3cm,∠DAB≈74°,
∠ABC≈106°.
∴∠OAB≈37°,
∴∠DAB≈37°×2=74°,
∴∠ABO≈90°-37°=53°.
解:(1)在Rt△CDE中,
∴
解:(2)设OD=x cm,则OB=x cm,在Rt△AOC中,
解得x = ,即OD的长度为 cm.
解:在Rt△END中,
∴ND=
在Rt△EMD中,
∴MD=
∵MN=MD-ND=25,
∴
解得ED ≈ 24.63(m),
∴点E到地面的距离ED约为24.63m.
解:在Rt△ABC中,
∴AB=d1·tan40°=4×tan40°≈3.356(m),
在Rt△ABD中,
∴d2=
∴DC=d2-d1≈4.619-4=0.619≈0.62(m).
∴楼梯占用地面增加的长度DC约为0.62m.
解:如图,连接OR,由题意得∠BOR=90°,
∠ARO=30°,∠BRO=45°,∴OB=OR.
∵
∴OA=4·sin30°=
又∵
∴
∴AB=OB-OA=OR-OA≈3.464-2=1.464(km).
∴火箭从A到B处的平均速度为1.464÷5=0.2928(km/s)≈293m/s.
解:如图,∵
∴∠A≈40°,∴∠B=90°-∠A≈50°.
∵AC2=AD2+CD2,
∴AC=
∵
∴BC=AC·tan A≈6.0×tan40°≈5.0(cm).
∵
∴AB=
解:由题意得BD=400-124=276(m),CB2=1100-400=700(m),
∠BAA2=30°,∠CBB2=45°.
在Rt△ABD中,sin∠BAD=sin30°=
∴AB=2BD=2×276=552(m).
在Rt△BCB2中,sin∠CBB2=sin45°=
∴BC=
∴AB+BC≈552+989.95≈1542(m).
答:钢缆AB和BC的总长度约为1542 m.
D
解:过C作CD⊥AB于D.
在Rt△CAD中,sin A=
∴CD=b·sin A.
∴
即
证明:由(1)可知
同理
∴
∴bsin A=asin B,
∴
解:由(2)可知
∴
即
∴
∴∠B=60°,
又∵BD=8,在Rt△BCD中,BC=2BD=16,
∴
在Rt△ADC中,AD= ,
∴AB=AD+BD=2+8=10.
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
