4.1.2 45°,60°角的正弦值及用计算器求正弦值或锐角 课件(共18张PPT)
文档属性
| 名称 | 4.1.2 45°,60°角的正弦值及用计算器求正弦值或锐角 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 00:00:00 | ||
图片预览





文档简介
4.1.2 45°,60°角的正弦值
及用计算器求正弦值或锐角
湘教版·九年级数学上册
新课导入
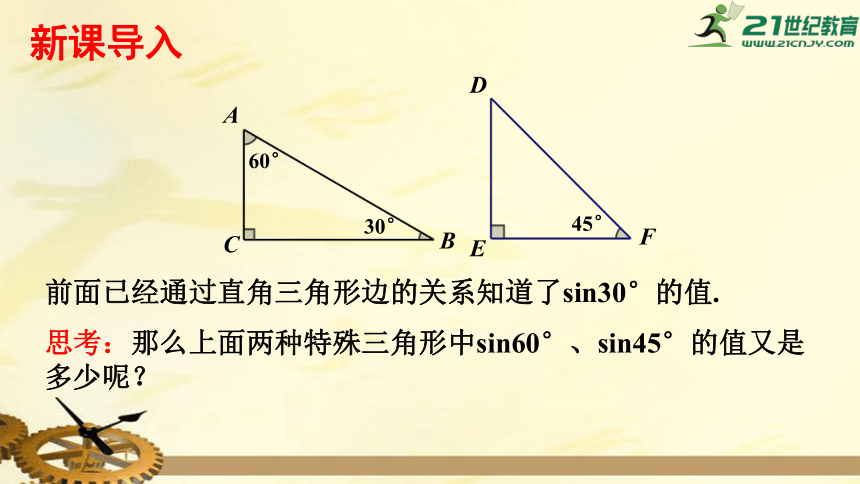
前面已经通过直角三角形边的关系知道了sin30°的值.
思考:那么上面两种特殊三角形中sin60°、sin45°的值又是多少呢?
30°
60°
45°
A
C
B
D
E
F
探究新知
动脑筋
如何求sin 45°的值?
如图,构造一个Rt△ABC,使∠C=90°,∠A=45°.
于是∠B=45°.
从而AC=BC.
根据勾股定理,得
AB2=AC2+BC2=2BC2.
于是AB= BC.
因此sin45°= .
如何求sin 60°的值?
如图所示,构造一个Rt△ABC ,使∠B=60°,则∠A=30°.
从而BC= AB. 根据勾股定理得
AC2=AB2-BC2=AB2-( AB)2= AB2.
于是AC= AB.
因此sin60°=
30°
60°
45°
A
C
B
D
E
F
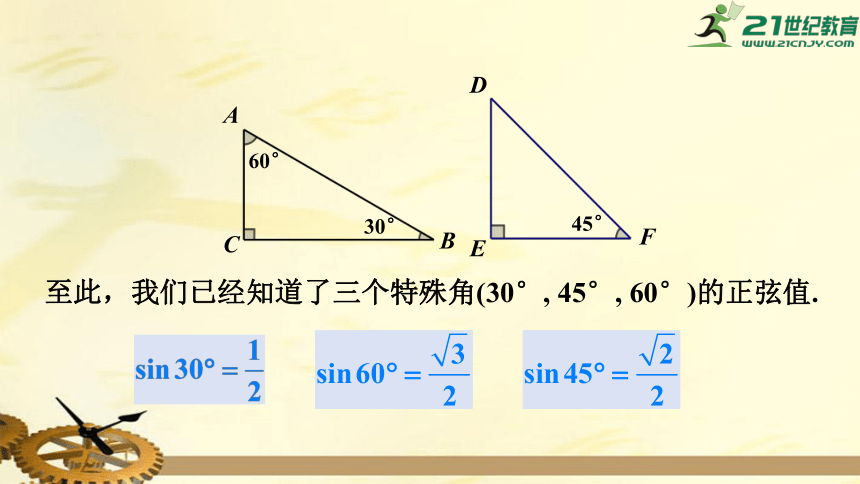
至此,我们已经知道了三个特殊角(30°, 45°, 60°)的正弦值.
对于一般锐角α的正弦值,我们可以利用计算器来求.
用计算器求锐角的正弦值要用到sin键.
例如求50°角的正弦值,可以在计算器上依次按键
,显示结果为0.766 0….
sin
5
0
如果已知正弦值,我们也可以利用计算器求出它的对应锐角.
例如,已知sinα=0.7071,依次按键
sin
2ndF
0
.
7
0
7
1
,
显示结果为44.999…,表示角α约等于45°.
做一做
利用计算器计算:
(1)sin40°≈ ______________(精确到0.0001);
(2)sin15°30′≈ ______________(精确到0.0001);
(3)若sin α=0.522 5,则 α ≈ ____________(精确到0.1°);
(4)若sin α=0.809 0,则 α ≈ ____________(精确到0.1°).
0.6428
0.2672
31.5°
54.0 °
例2:计算:
解:
小 结:
1.直角三角形中,角α的正弦函数等于哪两边之比呢?
2.直角三角形中,sin α值的范围是什么?
3.学习角α的正弦函数时,用到了什么主要的数学思想方法?
练习
1.用计算器求下列锐角的正弦值(精确到0.0001):
(1)35°; (2)65°36′; (3)80°54′.
解:(1)sin35°=0.5736;
(2)sin65°36′=0.9107;
(3)sin80°54′=0.9874.
2.已知下列正弦值,用计算器求对应的锐角(精确到0.1°):
(1)sin α =0.8071; (2)sin α =0.8660.
解:(1)α ≈ 53.8°;
(2)α ≈ 60.0°;
3.计算:
(1) sin260°+sin245°; (2) 1-2sin30°sin60°.
解:sin260°+sin245°
解:1-2sin30°sin60°
4.如图,一名患者体内某器官后面有一肿瘤,在接受放射性治疗时,为了最大限度地保证疗效,并且防止伤害器官,射线必须从侧面照射肿瘤,已知肿瘤在皮下6.3cm的A处,射线从肿瘤右侧9.8cm的B处进入身体,求∠CBA的度数.
解:在Rt△ABC中,由勾股定理可得
AB2= AC2+BC2= 6.32+9.82=135.73.
于是AB≈11.65.
因此
则∠CAB≈32°44′.
课堂小结
30°
60°
45°
A
C
B
D
E
F
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
及用计算器求正弦值或锐角
湘教版·九年级数学上册
新课导入
前面已经通过直角三角形边的关系知道了sin30°的值.
思考:那么上面两种特殊三角形中sin60°、sin45°的值又是多少呢?
30°
60°
45°
A
C
B
D
E
F
探究新知
动脑筋
如何求sin 45°的值?
如图,构造一个Rt△ABC,使∠C=90°,∠A=45°.
于是∠B=45°.
从而AC=BC.
根据勾股定理,得
AB2=AC2+BC2=2BC2.
于是AB= BC.
因此sin45°= .
如何求sin 60°的值?
如图所示,构造一个Rt△ABC ,使∠B=60°,则∠A=30°.
从而BC= AB. 根据勾股定理得
AC2=AB2-BC2=AB2-( AB)2= AB2.
于是AC= AB.
因此sin60°=
30°
60°
45°
A
C
B
D
E
F
至此,我们已经知道了三个特殊角(30°, 45°, 60°)的正弦值.
对于一般锐角α的正弦值,我们可以利用计算器来求.
用计算器求锐角的正弦值要用到sin键.
例如求50°角的正弦值,可以在计算器上依次按键
,显示结果为0.766 0….
sin
5
0
如果已知正弦值,我们也可以利用计算器求出它的对应锐角.
例如,已知sinα=0.7071,依次按键
sin
2ndF
0
.
7
0
7
1
,
显示结果为44.999…,表示角α约等于45°.
做一做
利用计算器计算:
(1)sin40°≈ ______________(精确到0.0001);
(2)sin15°30′≈ ______________(精确到0.0001);
(3)若sin α=0.522 5,则 α ≈ ____________(精确到0.1°);
(4)若sin α=0.809 0,则 α ≈ ____________(精确到0.1°).
0.6428
0.2672
31.5°
54.0 °
例2:计算:
解:
小 结:
1.直角三角形中,角α的正弦函数等于哪两边之比呢?
2.直角三角形中,sin α值的范围是什么?
3.学习角α的正弦函数时,用到了什么主要的数学思想方法?
练习
1.用计算器求下列锐角的正弦值(精确到0.0001):
(1)35°; (2)65°36′; (3)80°54′.
解:(1)sin35°=0.5736;
(2)sin65°36′=0.9107;
(3)sin80°54′=0.9874.
2.已知下列正弦值,用计算器求对应的锐角(精确到0.1°):
(1)sin α =0.8071; (2)sin α =0.8660.
解:(1)α ≈ 53.8°;
(2)α ≈ 60.0°;
3.计算:
(1) sin260°+sin245°; (2) 1-2sin30°sin60°.
解:sin260°+sin245°
解:1-2sin30°sin60°
4.如图,一名患者体内某器官后面有一肿瘤,在接受放射性治疗时,为了最大限度地保证疗效,并且防止伤害器官,射线必须从侧面照射肿瘤,已知肿瘤在皮下6.3cm的A处,射线从肿瘤右侧9.8cm的B处进入身体,求∠CBA的度数.
解:在Rt△ABC中,由勾股定理可得
AB2= AC2+BC2= 6.32+9.82=135.73.
于是AB≈11.65.
因此
则∠CAB≈32°44′.
课堂小结
30°
60°
45°
A
C
B
D
E
F
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
谢谢观看
THANKS
谢谢大家!
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
