课时分层作业12 三角函数的简单应用-2021秋北师大版高中数学必修四练习(word含答案解析)
文档属性
| 名称 | 课时分层作业12 三角函数的简单应用-2021秋北师大版高中数学必修四练习(word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 321.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 11:56:38 | ||
图片预览




文档简介
课时分层作业(十二) 三角函数的简单应用
(建议用时:40分钟)
一、选择题
1.如图是一向右传播的绳波在某一时刻绳子各点的位置图,经过周期后,乙的位置将移至( )
A.甲 B.乙
C.丙 D.丁
2.电流I(A)随时间t(s)变化的关系式是I=5sin ,则当t=时,电流I为( )
A.5 B.
C.2 D.-5
3.某城市6月份的平均气温最高,为29.45°C;12月份平均气温最低,为18.35°C.若x月份的平均气温为y°C,满足条件的一个模拟函数可以是( )
A.y=23.9-5.55sin x B.y=23.9-5.55cos x
C.y=23.9-5.55tan x D.y=23.9+5.55cos x
4.一根长l cm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式是s=3cos ,其中g是重力加速度,当小球摆动的周期是1 s时,线长l等于( )
A. B.
C. D.
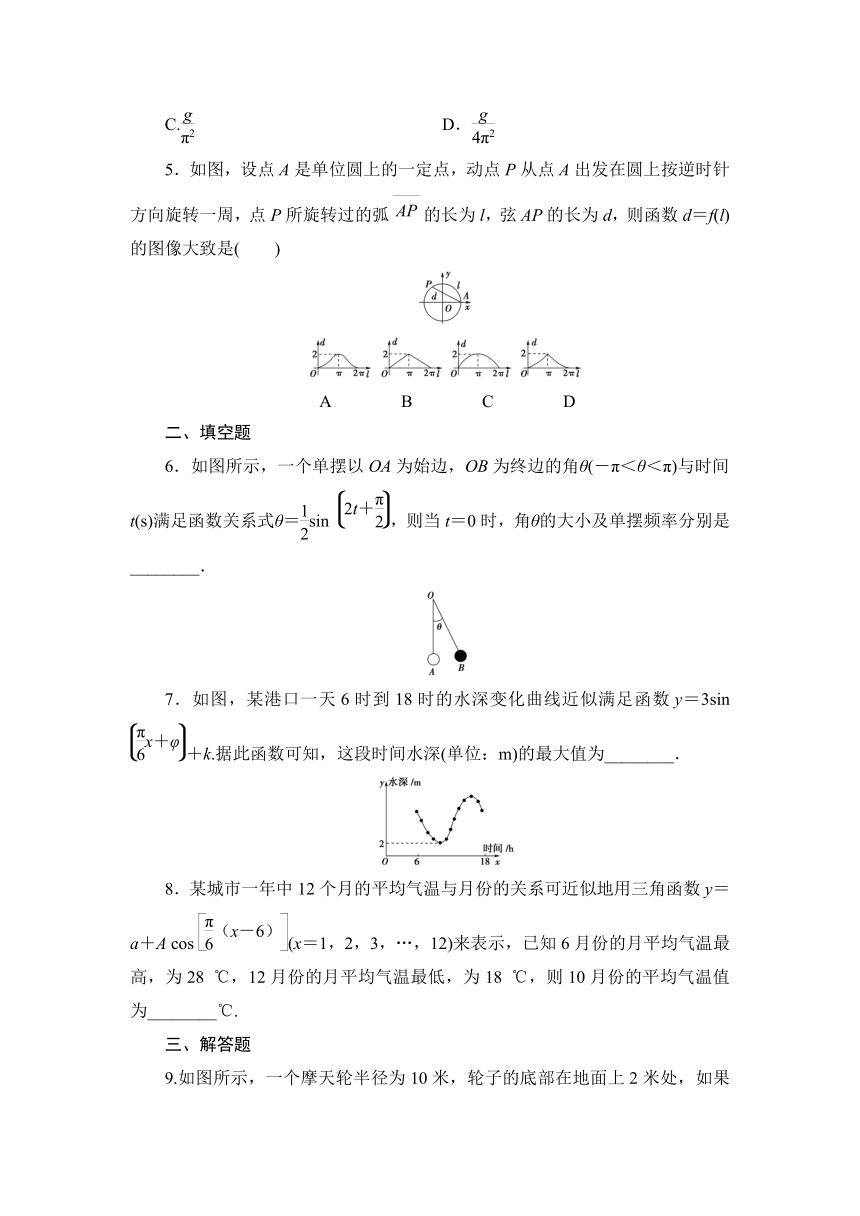
5.如图,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图像大致是( )
A B C D
二、填空题
6.如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=sin ,则当t=0时,角θ的大小及单摆频率分别是________.
7.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin +k.据此函数可知,这段时间水深(单位:m)的最大值为________.
8.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y=a+A cos (x=1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28 ℃,12月份的月平均气温最低,为18 ℃,则10月份的平均气温值为________℃.
三、解答题
9.如图所示,一个摩天轮半径为10米,轮子的底部在地面上2米处,如果此摩天轮每20分钟转一圈,且当摩天轮上某人经过点P处(点P与摩天轮中心O高度相同)时开始计时(按逆时针方向转).
(1)求此人相对于地面的高度关于时间的函数关系式;
(2)在摩天轮转动的一圈内,有多长时间此人相对于地面的高度不超过10米.
10.如图,某动物种群数量1月1日(t=0时)低至700,7月1日高至900,其总量在此两值之间按照正弦型曲线变化.
(1)求出种群数量y关于时间t的函数表达式(其中t以年初以来的月为计量单位);
(2)估计当年3月1日动物种群数量.
1.一半径为10的水轮,水轮的圆心到水面的距离为7,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y与时间x(秒)满足函数关系式y=A sin (ωx+φ)+7,则( )
A.ω=,A=10 B.ω=,A=10
C.ω=,A=17 D.ω= ,A=17
2.一种波的波形为函数y=-sin x的图像,若其在区间[0,t]上至少有2个波峰(图像的最高点),则正整数t的最小值是( )
A.5 B.6 C.7 D.8
3.某星星的亮度变化周期为10天,此星星的平均亮度为3.8等量,最高亮度距平均亮度0.2等量,则可近似地描述此星星亮度与时间关系的一个三角函数式为________.
4.设偶函数f(x)=A sin (ωx+φ)(A>0,ω>0,0<φ<π)的部分图像如图所示,△KLM为等腰直角三角形,∠KML=90°,|KL|=1,则f的值为________.
5.在一个港口,相邻两次高潮发生时间相距12 h,低潮时水的深度为8.4 m,高潮时为16 m,一次高潮发生在10月10日4:00.每天涨潮落潮时,水的深度d(m)与时间t(h)近似满足关系式d=A sin (ωt+φ)+h.
(1)若从10月10日0:00开始计算时间,选用一个三角函数来近似描述该港口的水深d(m)和时间t(h)之间的函数关系;
(2)10月10日17:00该港口水深约为多少?(精确到0.1 m)
(3)10月10日这一天该港口共有多少时间水深低于10.3 m?
课时分层作业(十二) 三角函数的简单应用
(建议用时:40分钟)
一、选择题
1.如图是一向右传播的绳波在某一时刻绳子各点的位置图,经过周期后,乙的位置将移至( )
A.甲 B.乙
C.丙 D.丁
C [因为相邻的最大值与最小值之间间隔区间长度相差半个周期,所以乙的位置将移至丙处.]
2.电流I(A)随时间t(s)变化的关系式是I=5sin ,则当t=时,电流I为( )
A.5 B.
C.2 D.-5
B [把t=代入I=5sin =5sin =,故选B.]
3.某城市6月份的平均气温最高,为29.45°C;12月份平均气温最低,为18.35°C.若x月份的平均气温为y°C,满足条件的一个模拟函数可以是( )
A.y=23.9-5.55sin x B.y=23.9-5.55cos x
C.y=23.9-5.55tan x D.y=23.9+5.55cos x
B [将x=6,x=12分别代入验证可知,只有B项符合要求,故选B.]
4.一根长l cm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式是s=3cos ,其中g是重力加速度,当小球摆动的周期是1 s时,线长l等于( )
A. B.
C. D.
D [∵T=,∴==2π,∴l=.]
5.如图,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图像大致是( )
A B C D
C [由l=αR可知α=,结合圆的几何性质可知=R sin ,所以d=2R sin =2R sin ,又R=1,所以d=2sin ,故结合正弦函数图像可知,选C.]
二、填空题
6.如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=sin ,则当t=0时,角θ的大小及单摆频率分别是________.
, [t=0时,θ=sin =,由函数解析式易知单摆周期为=π,故频率为.]
7.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin +k.据此函数可知,这段时间水深(单位:m)的最大值为________.
8 [根据图像得函数的最小值为2,有-3+k=2,k=5,最大值为3+k=8.]
8.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y=a+A cos (x=1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28 ℃,12月份的月平均气温最低,为18 ℃,则10月份的平均气温值为________℃.
20.5 [由题意可知,A==5,
a==23.
从而,y=5cos +23,
故10月份的平均气温值为
y=5cos +23=20.5 ℃.]
三、解答题
9.如图所示,一个摩天轮半径为10米,轮子的底部在地面上2米处,如果此摩天轮每20分钟转一圈,且当摩天轮上某人经过点P处(点P与摩天轮中心O高度相同)时开始计时(按逆时针方向转).
(1)求此人相对于地面的高度关于时间的函数关系式;
(2)在摩天轮转动的一圈内,有多长时间此人相对于地面的高度不超过10米.
[解] (1)以O为坐标原点,以OP所在直线为x轴建立平面直角坐标系(略),设摩天轮上某人在Q处,则在t分钟内OQ转过的角为t,所以t分钟时,Q点的纵坐标为10·sin ·t,故在t分钟时此人相对于地面的高度为
y=10sin t+12(米).
(2)令y=10sin t+12≤10,则sin t≤-,
因为0≤t≤20,所以10.64≤t≤19.36,故约有8.72分钟此人相对于地面的高度不超过10米.
10.如图,某动物种群数量1月1日(t=0时)低至700,7月1日高至900,其总量在此两值之间按照正弦型曲线变化.
(1)求出种群数量y关于时间t的函数表达式(其中t以年初以来的月为计量单位);
(2)估计当年3月1日动物种群数量.
[解] (1)设种群数量y关于t的解析式为y=A sin (ωt+φ)+b(A>0,ω>0),
则解得A=100,b=800.
又周期T=2×6=12,∴ω==,
∴y=100sin +800.
又当t=6时,y=900,
∴900=100sin +800,
∴sin (π+φ)=1,
∴sin φ=-1,∴可取φ=-,
∴y=100sin +800.
(2)当t=2时,
y=100sin +800=750,
即当年3月1日动物种群数量约是750.
1.一半径为10的水轮,水轮的圆心到水面的距离为7,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y与时间x(秒)满足函数关系式y=A sin (ωx+φ)+7,则( )
A.ω=,A=10 B.ω=,A=10
C.ω=,A=17 D.ω= ,A=17
A [T==15,ω=,A=10.]
2.一种波的波形为函数y=-sin x的图像,若其在区间[0,t]上至少有2个波峰(图像的最高点),则正整数t的最小值是( )
A.5 B.6 C.7 D.8
C [由y=-sin 的图像知,要使在区间[0,t]上至少有2个波峰,必须使区间[0,t]的长度不小于2T-=,即t≥·=·=7,故选C.]
3.某星星的亮度变化周期为10天,此星星的平均亮度为3.8等量,最高亮度距平均亮度0.2等量,则可近似地描述此星星亮度与时间关系的一个三角函数式为________.
y=0.2sin t+3.8(t>0)(答案不唯一) [假设三角函数模型为y=A sin ωt+b,
由题意知,A=0.2,b=3.8,T=10,
∴ω==,∴y=0.2sin t+3.8(t>0).]
4.设偶函数f(x)=A sin (ωx+φ)(A>0,ω>0,0<φ<π)的部分图像如图所示,△KLM为等腰直角三角形,∠KML=90°,|KL|=1,则f的值为________.
[取K,L中点N(图略),则MN=,
因此A=,由T=2得ω=π.
∵函数为偶函数,0<φ<π,∴φ=,
∴f(x)=cos πx,∴f=cos =.]
5.在一个港口,相邻两次高潮发生时间相距12 h,低潮时水的深度为8.4 m,高潮时为16 m,一次高潮发生在10月10日4:00.每天涨潮落潮时,水的深度d(m)与时间t(h)近似满足关系式d=A sin (ωt+φ)+h.
(1)若从10月10日0:00开始计算时间,选用一个三角函数来近似描述该港口的水深d(m)和时间t(h)之间的函数关系;
(2)10月10日17:00该港口水深约为多少?(精确到0.1 m)
(3)10月10日这一天该港口共有多少时间水深低于10.3 m?
[解] (1)依题意知T==12,
故ω=,h==12.2,
A=16-12.2=3.8,
所以d=3.8sin +12.2.
又因为t=4时,d=16,
所以sin =1,
所以φ=-,
所以d=3.8sin +12.2.
(2)t=17时,d=3.8sin +12.2=3.8sin +12.2≈15.5(m).
(3)令3.8sin +12.2<10.3,
有sin <-,
因此2kπ+<t-<2kπ+(k∈Z),
所以2kπ+<t<2kπ+2π,k∈Z,
所以12k+8<t<12k+12,k∈Z.
令k=0,得t∈(8,12);
令k=1,得t∈(20,24).
故这一天共有8 h水深低于10.3 m.
(建议用时:40分钟)
一、选择题
1.如图是一向右传播的绳波在某一时刻绳子各点的位置图,经过周期后,乙的位置将移至( )
A.甲 B.乙
C.丙 D.丁
2.电流I(A)随时间t(s)变化的关系式是I=5sin ,则当t=时,电流I为( )
A.5 B.
C.2 D.-5
3.某城市6月份的平均气温最高,为29.45°C;12月份平均气温最低,为18.35°C.若x月份的平均气温为y°C,满足条件的一个模拟函数可以是( )
A.y=23.9-5.55sin x B.y=23.9-5.55cos x
C.y=23.9-5.55tan x D.y=23.9+5.55cos x
4.一根长l cm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式是s=3cos ,其中g是重力加速度,当小球摆动的周期是1 s时,线长l等于( )
A. B.
C. D.
5.如图,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图像大致是( )
A B C D
二、填空题
6.如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=sin ,则当t=0时,角θ的大小及单摆频率分别是________.
7.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin +k.据此函数可知,这段时间水深(单位:m)的最大值为________.
8.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y=a+A cos (x=1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28 ℃,12月份的月平均气温最低,为18 ℃,则10月份的平均气温值为________℃.
三、解答题
9.如图所示,一个摩天轮半径为10米,轮子的底部在地面上2米处,如果此摩天轮每20分钟转一圈,且当摩天轮上某人经过点P处(点P与摩天轮中心O高度相同)时开始计时(按逆时针方向转).
(1)求此人相对于地面的高度关于时间的函数关系式;
(2)在摩天轮转动的一圈内,有多长时间此人相对于地面的高度不超过10米.
10.如图,某动物种群数量1月1日(t=0时)低至700,7月1日高至900,其总量在此两值之间按照正弦型曲线变化.
(1)求出种群数量y关于时间t的函数表达式(其中t以年初以来的月为计量单位);
(2)估计当年3月1日动物种群数量.
1.一半径为10的水轮,水轮的圆心到水面的距离为7,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y与时间x(秒)满足函数关系式y=A sin (ωx+φ)+7,则( )
A.ω=,A=10 B.ω=,A=10
C.ω=,A=17 D.ω= ,A=17
2.一种波的波形为函数y=-sin x的图像,若其在区间[0,t]上至少有2个波峰(图像的最高点),则正整数t的最小值是( )
A.5 B.6 C.7 D.8
3.某星星的亮度变化周期为10天,此星星的平均亮度为3.8等量,最高亮度距平均亮度0.2等量,则可近似地描述此星星亮度与时间关系的一个三角函数式为________.
4.设偶函数f(x)=A sin (ωx+φ)(A>0,ω>0,0<φ<π)的部分图像如图所示,△KLM为等腰直角三角形,∠KML=90°,|KL|=1,则f的值为________.
5.在一个港口,相邻两次高潮发生时间相距12 h,低潮时水的深度为8.4 m,高潮时为16 m,一次高潮发生在10月10日4:00.每天涨潮落潮时,水的深度d(m)与时间t(h)近似满足关系式d=A sin (ωt+φ)+h.
(1)若从10月10日0:00开始计算时间,选用一个三角函数来近似描述该港口的水深d(m)和时间t(h)之间的函数关系;
(2)10月10日17:00该港口水深约为多少?(精确到0.1 m)
(3)10月10日这一天该港口共有多少时间水深低于10.3 m?
课时分层作业(十二) 三角函数的简单应用
(建议用时:40分钟)
一、选择题
1.如图是一向右传播的绳波在某一时刻绳子各点的位置图,经过周期后,乙的位置将移至( )
A.甲 B.乙
C.丙 D.丁
C [因为相邻的最大值与最小值之间间隔区间长度相差半个周期,所以乙的位置将移至丙处.]
2.电流I(A)随时间t(s)变化的关系式是I=5sin ,则当t=时,电流I为( )
A.5 B.
C.2 D.-5
B [把t=代入I=5sin =5sin =,故选B.]
3.某城市6月份的平均气温最高,为29.45°C;12月份平均气温最低,为18.35°C.若x月份的平均气温为y°C,满足条件的一个模拟函数可以是( )
A.y=23.9-5.55sin x B.y=23.9-5.55cos x
C.y=23.9-5.55tan x D.y=23.9+5.55cos x
B [将x=6,x=12分别代入验证可知,只有B项符合要求,故选B.]
4.一根长l cm的线,一端固定,另一端悬挂一个小球,小球摆动时离开平衡位置的位移s(cm)与时间t(s)的函数关系式是s=3cos ,其中g是重力加速度,当小球摆动的周期是1 s时,线长l等于( )
A. B.
C. D.
D [∵T=,∴==2π,∴l=.]
5.如图,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图像大致是( )
A B C D
C [由l=αR可知α=,结合圆的几何性质可知=R sin ,所以d=2R sin =2R sin ,又R=1,所以d=2sin ,故结合正弦函数图像可知,选C.]
二、填空题
6.如图所示,一个单摆以OA为始边,OB为终边的角θ(-π<θ<π)与时间t(s)满足函数关系式θ=sin ,则当t=0时,角θ的大小及单摆频率分别是________.
, [t=0时,θ=sin =,由函数解析式易知单摆周期为=π,故频率为.]
7.如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin +k.据此函数可知,这段时间水深(单位:m)的最大值为________.
8 [根据图像得函数的最小值为2,有-3+k=2,k=5,最大值为3+k=8.]
8.某城市一年中12个月的平均气温与月份的关系可近似地用三角函数y=a+A cos (x=1,2,3,…,12)来表示,已知6月份的月平均气温最高,为28 ℃,12月份的月平均气温最低,为18 ℃,则10月份的平均气温值为________℃.
20.5 [由题意可知,A==5,
a==23.
从而,y=5cos +23,
故10月份的平均气温值为
y=5cos +23=20.5 ℃.]
三、解答题
9.如图所示,一个摩天轮半径为10米,轮子的底部在地面上2米处,如果此摩天轮每20分钟转一圈,且当摩天轮上某人经过点P处(点P与摩天轮中心O高度相同)时开始计时(按逆时针方向转).
(1)求此人相对于地面的高度关于时间的函数关系式;
(2)在摩天轮转动的一圈内,有多长时间此人相对于地面的高度不超过10米.
[解] (1)以O为坐标原点,以OP所在直线为x轴建立平面直角坐标系(略),设摩天轮上某人在Q处,则在t分钟内OQ转过的角为t,所以t分钟时,Q点的纵坐标为10·sin ·t,故在t分钟时此人相对于地面的高度为
y=10sin t+12(米).
(2)令y=10sin t+12≤10,则sin t≤-,
因为0≤t≤20,所以10.64≤t≤19.36,故约有8.72分钟此人相对于地面的高度不超过10米.
10.如图,某动物种群数量1月1日(t=0时)低至700,7月1日高至900,其总量在此两值之间按照正弦型曲线变化.
(1)求出种群数量y关于时间t的函数表达式(其中t以年初以来的月为计量单位);
(2)估计当年3月1日动物种群数量.
[解] (1)设种群数量y关于t的解析式为y=A sin (ωt+φ)+b(A>0,ω>0),
则解得A=100,b=800.
又周期T=2×6=12,∴ω==,
∴y=100sin +800.
又当t=6时,y=900,
∴900=100sin +800,
∴sin (π+φ)=1,
∴sin φ=-1,∴可取φ=-,
∴y=100sin +800.
(2)当t=2时,
y=100sin +800=750,
即当年3月1日动物种群数量约是750.
1.一半径为10的水轮,水轮的圆心到水面的距离为7,已知水轮每分钟旋转4圈,水轮上的点P到水面距离y与时间x(秒)满足函数关系式y=A sin (ωx+φ)+7,则( )
A.ω=,A=10 B.ω=,A=10
C.ω=,A=17 D.ω= ,A=17
A [T==15,ω=,A=10.]
2.一种波的波形为函数y=-sin x的图像,若其在区间[0,t]上至少有2个波峰(图像的最高点),则正整数t的最小值是( )
A.5 B.6 C.7 D.8
C [由y=-sin 的图像知,要使在区间[0,t]上至少有2个波峰,必须使区间[0,t]的长度不小于2T-=,即t≥·=·=7,故选C.]
3.某星星的亮度变化周期为10天,此星星的平均亮度为3.8等量,最高亮度距平均亮度0.2等量,则可近似地描述此星星亮度与时间关系的一个三角函数式为________.
y=0.2sin t+3.8(t>0)(答案不唯一) [假设三角函数模型为y=A sin ωt+b,
由题意知,A=0.2,b=3.8,T=10,
∴ω==,∴y=0.2sin t+3.8(t>0).]
4.设偶函数f(x)=A sin (ωx+φ)(A>0,ω>0,0<φ<π)的部分图像如图所示,△KLM为等腰直角三角形,∠KML=90°,|KL|=1,则f的值为________.
[取K,L中点N(图略),则MN=,
因此A=,由T=2得ω=π.
∵函数为偶函数,0<φ<π,∴φ=,
∴f(x)=cos πx,∴f=cos =.]
5.在一个港口,相邻两次高潮发生时间相距12 h,低潮时水的深度为8.4 m,高潮时为16 m,一次高潮发生在10月10日4:00.每天涨潮落潮时,水的深度d(m)与时间t(h)近似满足关系式d=A sin (ωt+φ)+h.
(1)若从10月10日0:00开始计算时间,选用一个三角函数来近似描述该港口的水深d(m)和时间t(h)之间的函数关系;
(2)10月10日17:00该港口水深约为多少?(精确到0.1 m)
(3)10月10日这一天该港口共有多少时间水深低于10.3 m?
[解] (1)依题意知T==12,
故ω=,h==12.2,
A=16-12.2=3.8,
所以d=3.8sin +12.2.
又因为t=4时,d=16,
所以sin =1,
所以φ=-,
所以d=3.8sin +12.2.
(2)t=17时,d=3.8sin +12.2=3.8sin +12.2≈15.5(m).
(3)令3.8sin +12.2<10.3,
有sin <-,
因此2kπ+<t-<2kπ+(k∈Z),
所以2kπ+<t<2kπ+2π,k∈Z,
所以12k+8<t<12k+12,k∈Z.
令k=0,得t∈(8,12);
令k=1,得t∈(20,24).
故这一天共有8 h水深低于10.3 m.
