北师大版数学九年级上册专题:反比例函数与图形面积 课件(共13张PPT)
文档属性
| 名称 | 北师大版数学九年级上册专题:反比例函数与图形面积 课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 08:45:23 | ||
图片预览



文档简介
(共13张PPT)
北师大版
九年级
新知导入
A
问题1:若点A在反比例函数
的图像上,
,
则
S矩形ABOC
=
。
数
形
数
新知讲解
反比例函数与图形面积
.gsp
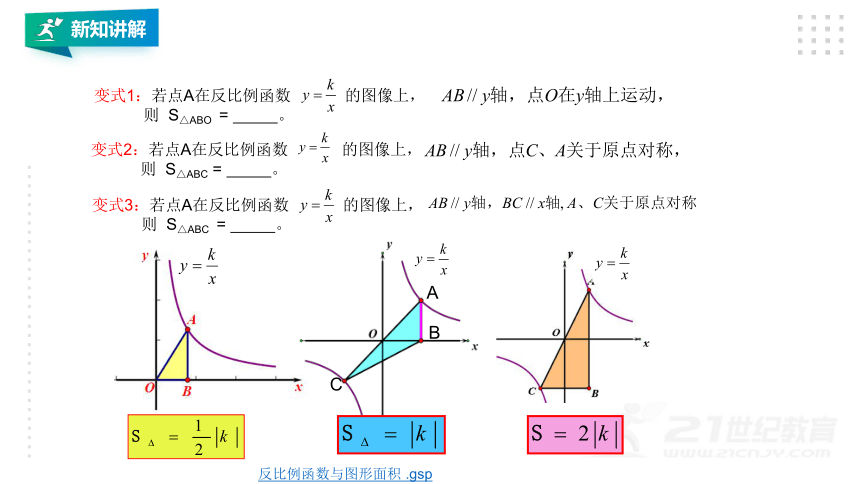
变式1:若点A在反比例函数
的图像上,
则
S△ABO
=
。
A
B
C
变式2:若点A在反比例函数
的图像上,
则
S△ABC
=
。
变式3:若点A在反比例函数
的图像上,
则
S△ABC
=
。
合作探究
问题2:(1)若点A、B分别在反比例函数
的图像上,
求
S△ABP
,你能想到哪些情形?
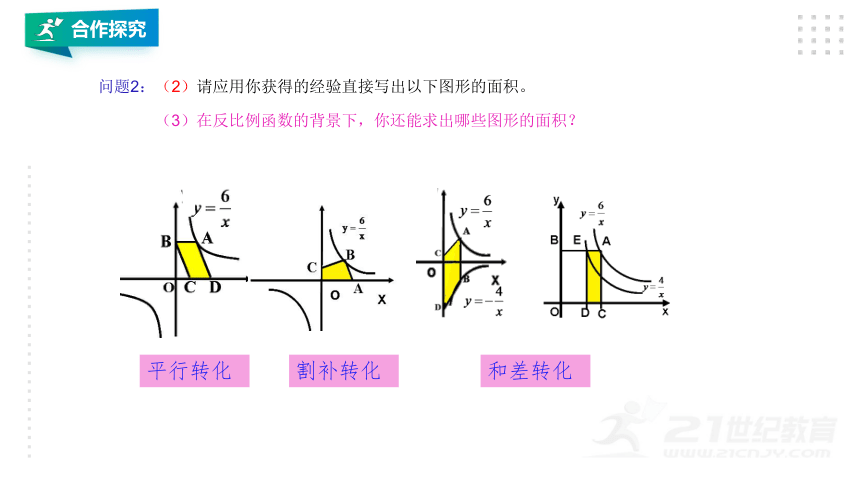
问题2:(2)请应用你获得的经验直接写出以下图形的面积。
(3)在反比例函数的背景下,你还能求出哪些图形的面积?
平行转化
割补转化
和差转化
合作探究
课堂练习
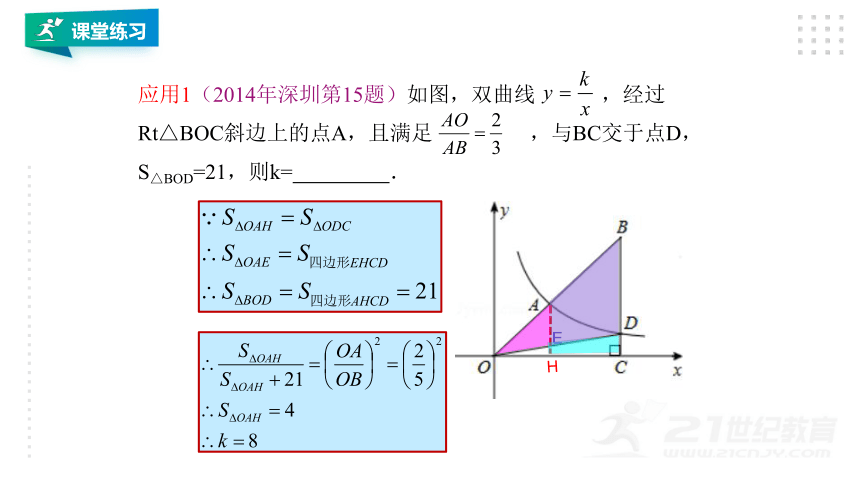
应用1(2014年深圳第15题)如图,双曲线
,经过Rt△BOC斜边上的点A,且满足
,与BC交于点D,S△BOD=21,则k=
.
H
E
课堂练习
应用2(2015年深圳第16题)如图,已知点A在反比例函数
上,作RT⊿ABC,点D为斜边AC的中点,连DB并延长交y轴于点E,若⊿BCE的面积为8,则k=
.
课堂练习
应用3(2020年广东第24题)如图,点B是反比例函数
图象上一点,过点B分别向坐标轴作垂线,垂足为A,C.反比例函数
的图象经过OB的中点M,与AB,BC分别相交于点D,E.连接DE并延长交x轴于点F,点G与点O关于点C对称,连接BF,BG.
(1)填空:k=
;
(2)求△BDF的面积;
(3)求证:四边形BDFG为平行四边形.
H
课堂小结
1.通过本节课的学习,在反比例函数背景下,你会求哪些图形的面积?请归类整理。
2.通过本节课的学习,你积累了哪些数学模型,这些模型之间有什么联系与区别?
3.通过本节课的学习,你掌握了哪些解题的策略和方法?
基本图形
平行转化
对称转化
和差转化
割补转化
数形结合
分解化归
数学建模
数
形
数
延伸拓展
过原点O的另一条直线l交双曲线
(k>0)于P、Q两点(P点在第一象限),若由点A、B、P、Q为顶点组成的四边形面积为24,求P点的坐标。
o
x
y
A
B
延伸拓展
P(2,4)或P(8,1)
P
Q
P
Q
分类讨论:
1.点P在点A的上方
2.点P在点A的下方
https://www.21cnjy.com/help/help_extract.php
北师大版
九年级
新知导入
A
问题1:若点A在反比例函数
的图像上,
,
则
S矩形ABOC
=
。
数
形
数
新知讲解
反比例函数与图形面积
.gsp
变式1:若点A在反比例函数
的图像上,
则
S△ABO
=
。
A
B
C
变式2:若点A在反比例函数
的图像上,
则
S△ABC
=
。
变式3:若点A在反比例函数
的图像上,
则
S△ABC
=
。
合作探究
问题2:(1)若点A、B分别在反比例函数
的图像上,
求
S△ABP
,你能想到哪些情形?
问题2:(2)请应用你获得的经验直接写出以下图形的面积。
(3)在反比例函数的背景下,你还能求出哪些图形的面积?
平行转化
割补转化
和差转化
合作探究
课堂练习
应用1(2014年深圳第15题)如图,双曲线
,经过Rt△BOC斜边上的点A,且满足
,与BC交于点D,S△BOD=21,则k=
.
H
E
课堂练习
应用2(2015年深圳第16题)如图,已知点A在反比例函数
上,作RT⊿ABC,点D为斜边AC的中点,连DB并延长交y轴于点E,若⊿BCE的面积为8,则k=
.
课堂练习
应用3(2020年广东第24题)如图,点B是反比例函数
图象上一点,过点B分别向坐标轴作垂线,垂足为A,C.反比例函数
的图象经过OB的中点M,与AB,BC分别相交于点D,E.连接DE并延长交x轴于点F,点G与点O关于点C对称,连接BF,BG.
(1)填空:k=
;
(2)求△BDF的面积;
(3)求证:四边形BDFG为平行四边形.
H
课堂小结
1.通过本节课的学习,在反比例函数背景下,你会求哪些图形的面积?请归类整理。
2.通过本节课的学习,你积累了哪些数学模型,这些模型之间有什么联系与区别?
3.通过本节课的学习,你掌握了哪些解题的策略和方法?
基本图形
平行转化
对称转化
和差转化
割补转化
数形结合
分解化归
数学建模
数
形
数
延伸拓展
过原点O的另一条直线l交双曲线
(k>0)于P、Q两点(P点在第一象限),若由点A、B、P、Q为顶点组成的四边形面积为24,求P点的坐标。
o
x
y
A
B
延伸拓展
P(2,4)或P(8,1)
P
Q
P
Q
分类讨论:
1.点P在点A的上方
2.点P在点A的下方
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
