2020-2021学年安徽省合肥市庐江县七年级(下)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年安徽省合肥市庐江县七年级(下)期末数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 954.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 00:00:00 | ||
图片预览



文档简介
2020-2021学年安徽省合肥市庐江县七年级(下)期末数学试卷
一、选择题(每小题4分,满分40分)
1.3的平方根是( )
A.9 B. C.﹣ D.±
2.若是二元一次方程x﹣my+3=0的解,则m的值为( )
A.6 B.4 C.0 D.
3.要了解学校在新冠肺炎防控中的有关情况,下面适合用抽样调查的是( )
①了解各校口罩、洗手液、消毒液的储备情况;
②了解师生在假期的离校情况;
③了解师生入校时的体温情况;
④了解师生对“七步洗手法”的运用情况.
A.① B.② C.③ D.④
4.若a<b,则下列变形错误的是( )
A.2a<2b B.2+a<2+b C.2﹣a<2﹣b D.a<b
5.庐江县是合肥市的南部副中心,以下能准确表示庐江县地理位置的是( )
A.在合肥市区的南部
B.东经117.48°
C.距离合肥79km处
D.东经117.48°北纬31.25°
6.如图,在下列条件中,不能判定直线a与b平行的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠5 D.∠3+∠4=180°
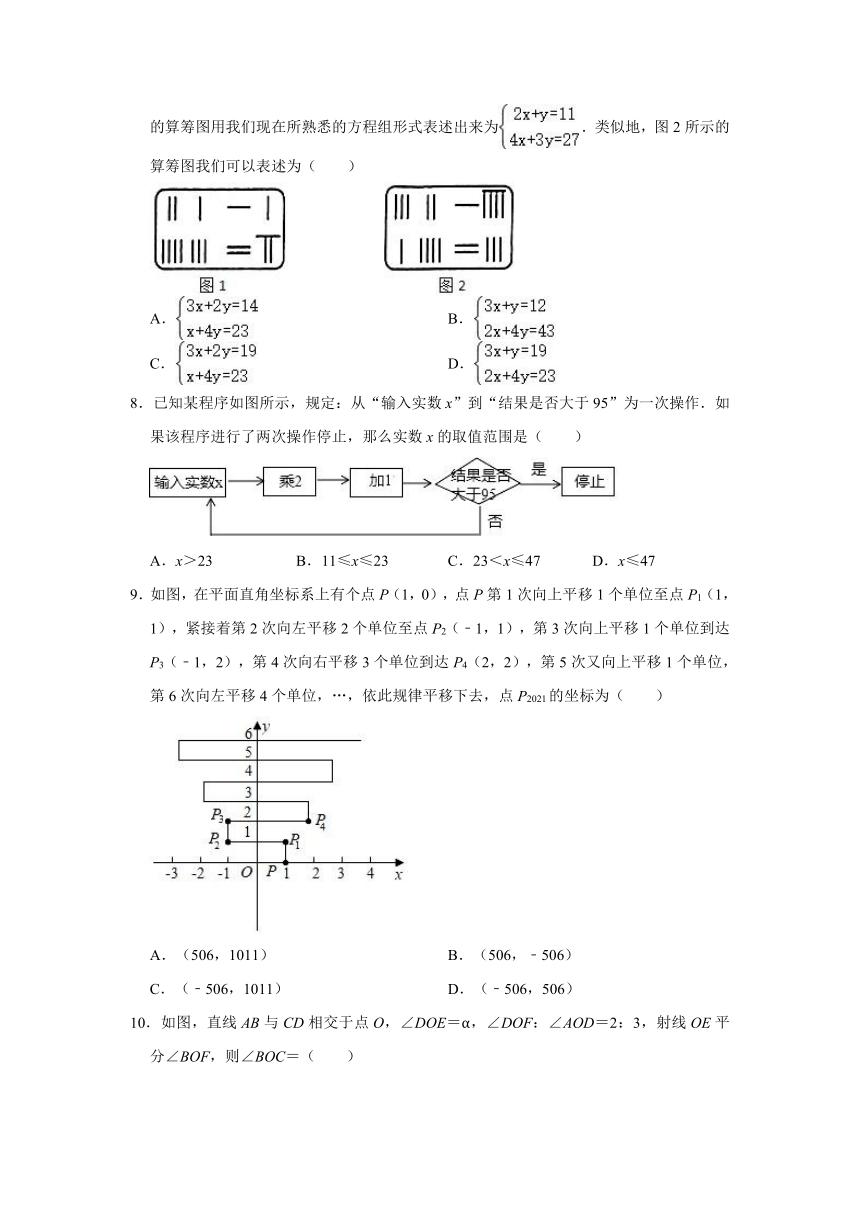
7.《九章算术》中的算筹图是竖排的,为看图方便我们把它改为横排,如图1,图2所示,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.图1表示的算筹图用我们现在所熟悉的方程组形式表述出来为.类似地,图2所示的算筹图我们可以表述为( )
A. B.
C. D.
8.已知某程序如图所示,规定:从“输入实数x”到“结果是否大于95”为一次操作.如果该程序进行了两次操作停止,那么实数x的取值范围是( )
A.x>23 B.11≤x≤23 C.23<x≤47 D.x≤47
9.如图,在平面直角坐标系上有个点P(1,0),点P第1次向上平移1个单位至点P1(1,1),紧接着第2次向左平移2个单位至点P2(﹣1,1),第3次向上平移1个单位到达P3(﹣1,2),第4次向右平移3个单位到达P4(2,2),第5次又向上平移1个单位,第6次向左平移4个单位,…,依此规律平移下去,点P2021的坐标为( )
A.(506,1011) B.(506,﹣506)
C.(﹣506,1011) D.(﹣506,506)
10.如图,直线AB与CD相交于点O,∠DOE=α,∠DOF:∠AOD=2:3,射线OE平分∠BOF,则∠BOC=( )
A.540°﹣5α B.540°﹣6α C.30° D.40°
二、填空题(本题共4小题,每小题5分,满分20分)
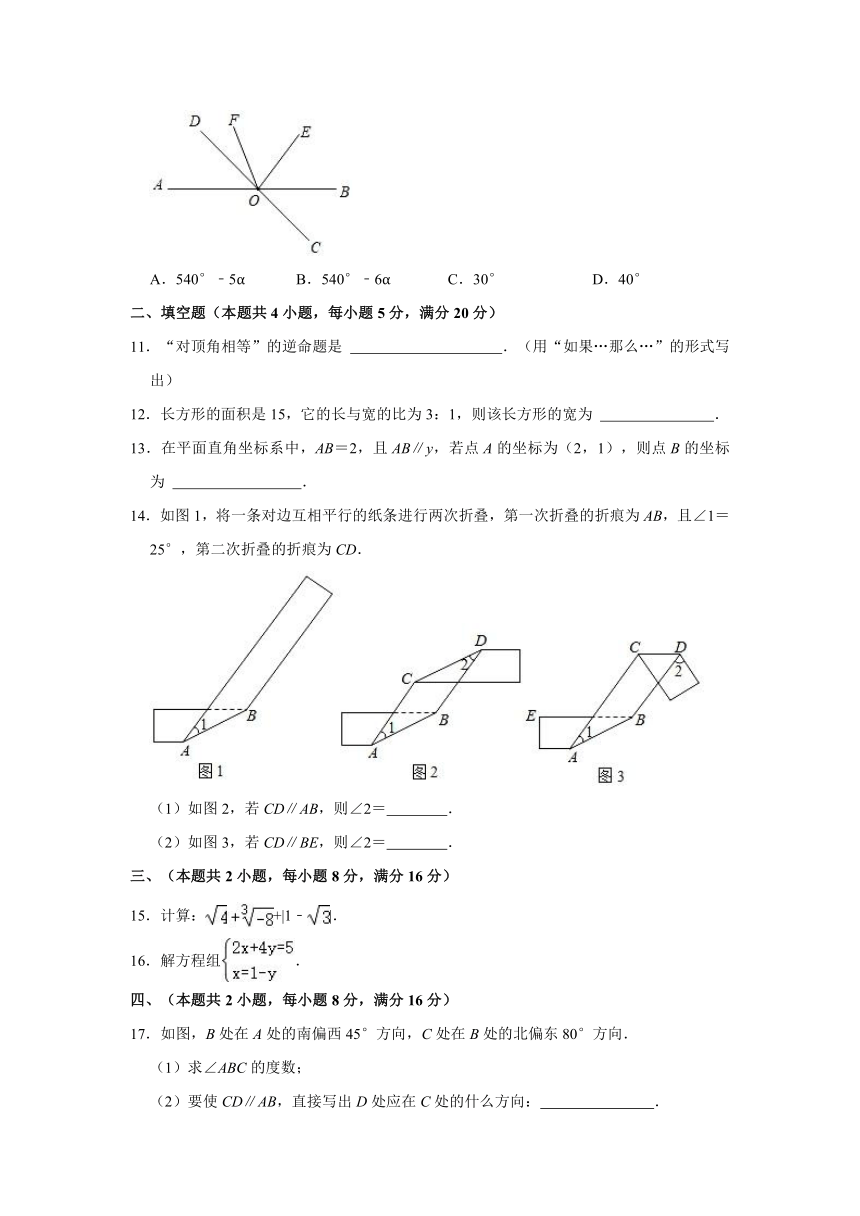
11.“对顶角相等”的逆命题是 .(用“如果…那么…”的形式写出)
12.长方形的面积是15,它的长与宽的比为3:1,则该长方形的宽为 .
13.在平面直角坐标系中,AB=2,且AB∥y,若点A的坐标为(2,1),则点B的坐标为 .
14.如图1,将一条对边互相平行的纸条进行两次折叠,第一次折叠的折痕为AB,且∠1=25°,第二次折叠的折痕为CD.
(1)如图2,若CD∥AB,则∠2= .
(2)如图3,若CD∥BE,则∠2= .
三、(本题共2小题,每小题8分,满分16分)
15.计算:+|1﹣|.
16.解方程组.
四、(本题共2小题,每小题8分,满分16分)
17.如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.
(1)求∠ABC的度数;
(2)要使CD∥AB,直接写出D处应在C处的什么方向: .
18.数轴上的点A、B依次表示两个实数.
(1)如图,在数轴上描出点A和点B的大致位置;
(2)如果点C在数轴上,且点C到点A的距离是,求点C所对应的实数.
五、(本题共2小题。每小题10分,满分20分)
19.解不等式组,并将解集在数轴上表示出来,并写出最小整数解.
20.△ABC在平面直角坐标系中的位置如图,现将△ABC先向上平移2个单位再向左平移5个单位得到△A1B1C1.
(1)画出△A1B1C1;
(2)写出点A1、B1、C1的坐标:A1 、B1 、C1 ;
(3)求△A1B1C1的面积.
六、(本题满分12分)
21.某校为了解学生近视情况,随机抽查了部分同学的视力,整理并制作出频数分布表和频数分布直方图(不完整).
请根据图表中提供的信息解答问题:
得分 频数 百分比
4.2≤x<4.4 5 m%
4.4≤x<4.6 15 7.5%
4.6≤x<4.8 60 30%
4.8≤x<5.0 n 45%
5.0≤x<5.2 30 15%
(1)在统计表中,m= ,n= ;
(2)补全频数分布直方图;
(3)若制作扇形统计图,则“4.6<x≤4.8”所在扇形的圆心角的度数为 ;
(4)该校有2000名学生,请你根据以上抽样调查结果,估计视力5.0以上(包括5.0)的学生有多少人.
七、(本题满分12分)
22.学校为了更新教学辅助设备,准备购买若干台电脑和打印机.如果购买1台电脑,2台打印机,需要花费5900元;如果购买2台电脑,2台打印机,需要花费9400元.
(1)求每台电脑和每台打印机的价格分别是多少元?
(2)如果学校购买电脑和打印机的预算费用不超过20000元,并且购买打印机的台数要比购买电脑的台数多1台,那么该学校至多能购买多少台打印机?
八、(本题满分14分)
23.如图1,AB⊥BC于点B,CD⊥BC于点C,点E在线段BC上,且AE⊥DE.
(1)求证:∠EAB=∠CED;
(2)如图2,AF、DF分别平分∠BAE和∠CDE,则∠F的度数是 (直接写出答案即可);
(3)如图3,EH平分∠CED,EH的反向延长线交∠BAE的平分线AF于点G.求证:EG⊥AF.(提示:三角形内角和等于180°)
参考答案
一、选择题(本题共10小题,每小题4分,满分40分。请将每小题唯一正确选项前的代号填入下面的答题栏内)
1.3的平方根是( )
A.9 B. C.﹣ D.±
解:∵()2=3,
∴3的平方根.
故选:D.
2.若是二元一次方程x﹣my+3=0的解,则m的值为( )
A.6 B.4 C.0 D.
解:将代入x﹣my+3=0中,可得3﹣m+3=0,
∴m=6,
故选:A.
3.要了解学校在新冠肺炎防控中的有关情况,下面适合用抽样调查的是( )
①了解各校口罩、洗手液、消毒液的储备情况;
②了解师生在假期的离校情况;
③了解师生入校时的体温情况;
④了解师生对“七步洗手法”的运用情况.
A.① B.② C.③ D.④
解:①了解各校口罩、洗手液、消毒液的储备情况,适宜采用全面调查;
②了解师生在假期的离校情况,适宜采用全面调查;
③了解师生入校时的体温情况,适宜采用全面调查;
④了解师生对“七步洗手法”的运用情况,适合用抽样调查;
故选:D.
4.若a<b,则下列变形错误的是( )
A.2a<2b B.2+a<2+b C.2﹣a<2﹣b D.a<b
解:∵a<b,
∴2a<2b,2+a<2+b,﹣a>﹣b,a<b,
∴2﹣a>2﹣b,
故选:C.
5.庐江县是合肥市的南部副中心,以下能准确表示庐江县地理位置的是( )
A.在合肥市区的南部
B.东经117.48°
C.距离合肥79km处
D.东经117.48°北纬31.25°
解:A、在合肥市区的南部,无法准确确定庐江县地理位置,不符合题意;
B、东经117.48°,无法准确确定庐江县地理位置,不符合题意;
C、距离合肥79km处,无法准确确定长沙地理位置无法准确确定庐江县地理位置,不符合题意;
D、东经117.48°北纬31.25°,是地球上唯一的点,能准确表示庐江县地理位置,符合题意;
故选:D.
6.如图,在下列条件中,不能判定直线a与b平行的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠5 D.∠3+∠4=180°
解:A、∵∠1=∠2,∴a∥b,不符合题意;
B、∵∠2=∠3,∴a∥b,不符合题意;
C、∵∠1与∠5既不是直线a,b被任何一条直线所截的一组同位角,内错角,
∴∠1=∠5,不能得到a∥b,
∴符合题意;
D、∵∠3+∠4=180°,∴a∥b,不符合题意;
故选:C.
7.《九章算术》中的算筹图是竖排的,为看图方便我们把它改为横排,如图1,图2所示,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.图1表示的算筹图用我们现在所熟悉的方程组形式表述出来为.类似地,图2所示的算筹图我们可以表述为( )
A. B.
C. D.
解:图2所示的算筹图我们可以表述为:.
故选:C.
8.已知某程序如图所示,规定:从“输入实数x”到“结果是否大于95”为一次操作.如果该程序进行了两次操作停止,那么实数x的取值范围是( )
A.x>23 B.11≤x≤23 C.23<x≤47 D.x≤47
解:第一次的结果为:2x+1,没有输出,则2x+1≤95,
解得:x≤47;
第二次的结果为:2(2x+1)+1=4x+3,输出,则4x+3>95,
解得:x>23;
综上可得:23<x≤47.
故选:C.
9.如图,在平面直角坐标系上有个点P(1,0),点P第1次向上平移1个单位至点P1(1,1),紧接着第2次向左平移2个单位至点P2(﹣1,1),第3次向上平移1个单位到达P3(﹣1,2),第4次向右平移3个单位到达P4(2,2),第5次又向上平移1个单位,第6次向左平移4个单位,…,依此规律平移下去,点P2021的坐标为( )
A.(506,1011) B.(506,﹣506)
C.(﹣506,1011) D.(﹣506,506)
解:设第n次跳动至点Pn,
观察发现:P(1,0),P1(1,1),P2(﹣1,1),P3(﹣1,2),P4(2,2),P5(2,3),P6(﹣2,3),P7(﹣2,4),P8(3,4),P9(3,5),…,
∴P4n(n+1,2n),P4n+1(n+1,2n+1),P4n+2(﹣n﹣1,2n+1),P4n+3(﹣n﹣1,2n+2)(n为自然数).
∵2021=505×4+1,
∴P2021(505+1,505×2+1),即(506,1011).
故选:A.
10.如图,直线AB与CD相交于点O,∠DOE=α,∠DOF:∠AOD=2:3,射线OE平分∠BOF,则∠BOC=( )
A.540°﹣5α B.540°﹣6α C.30° D.40°
解:设∠DOF=2x,∠AOD=3x,
∵∠DOE=α,
∴∠FOE=α﹣2x,
∵射线OE平分∠BOF,
∴∠BOE=∠EOF=α﹣2x,
则:3x+α+α﹣2x=180°,
解得:x=180°﹣2α,
∴∠AOD=3×(180°﹣2α)=540°﹣6α,
∴∠BOC=540°﹣6α,
故选:B.
二、填空题(本题共4小题,每小题5分,满分20分)
11.“对顶角相等”的逆命题是 如果两个角相等,那么这两个角是对顶角 .(用“如果…那么…”的形式写出)
解:命题“对顶角相等.”的逆命题:如果两个角相等,那么这两个角是对顶角,
故答案为:如果两个角相等,那么这两个角是对顶角.
12.长方形的面积是15,它的长与宽的比为3:1,则该长方形的宽为 .
解:设矩形的宽为x,则长为3x,
根据题意得:3x2=15,
所以x2=5.
解得:x=±(负值舍去),
∴长方形的宽为,
故答案为:.
13.在平面直角坐标系中,AB=2,且AB∥y,若点A的坐标为(2,1),则点B的坐标为 (2,﹣1)或(2,3) .
解:∵在平面直角坐标系中,AB=2,且AB∥y,若点A的坐标为(2,1),
∴点B的坐标为(2,﹣1)或(2,3).
故答案为:(2,﹣1)或(2,3).
14.如图1,将一条对边互相平行的纸条进行两次折叠,第一次折叠的折痕为AB,且∠1=25°,第二次折叠的折痕为CD.
(1)如图2,若CD∥AB,则∠2= 25° .
(2)如图3,若CD∥BE,则∠2= 80° .
解:(1)如图2,
∵CD∥AB,
∴∠1+∠ACD=180°,
∵∠1=25°,
∴∠ACD=180°﹣25°=155°,
∵AC∥BD,
∴∠ACD+∠2=180°,
∴∠2=180°﹣∠ACD=25°,
故答案为:25°;
(2)如图3,由折叠的性质,可得∠3=∠1=25°,
∵EB∥AM,
∴∠4=∠1+∠3=50°,
∵AC∥BD,
∴∠4+∠EBD=180°,
∴∠EBD=180°﹣∠4=130°,
又∵CD∥BE,
∴∠EBD+∠BDC=180°,
∴∠BDC=50°,
由折叠的性质,可得2∠BDC+∠2=180°,
∴∠2=180°﹣100°=80°,
故答案为:80°.
三、(本题共2小题,每小题8分,满分16分)
15.计算:+|1﹣|.
解:+|1﹣|
=2+(﹣2)+﹣1
=﹣1.
16.解方程组.
解:,
把②代入①,得2(1﹣y)+4y=5,
解得:y=,把y=代入②,得x=1﹣=﹣,
所以方程组的解是.
四、(本题共2小题,每小题8分,满分16分)
17.如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.
(1)求∠ABC的度数;
(2)要使CD∥AB,直接写出D处应在C处的什么方向: D在C的南偏西45° .
解:(1)如图,由题意得∠FAB=45°,
∵AF∥BE,
∴∠FAB=∠ABE=45°,
∵∠EBC=80°
∴∠ABC=35°;
(2)D在C的南偏西45°,理由如下:
∵CG∥BE,
∴∠GCB=∠EBC=80°,
∵∠GCD=45°
∴∠BCD=35°
∴∠ABC=∠BCD=35°,
∴CD∥AB.
故答案为:D在C的南偏西45°.
18.数轴上的点A、B依次表示两个实数.
(1)如图,在数轴上描出点A和点B的大致位置;
(2)如果点C在数轴上,且点C到点A的距离是,求点C所对应的实数.
解:(1)如图:
(2)设点C表示的数是x,则:
|x+|=2.
∴x=或﹣3.
∴点C表示的数是或﹣3.
五、(本题共2小题。每小题10分,满分20分)
19.解不等式组,并将解集在数轴上表示出来,并写出最小整数解.
解:解不等式2x<7(x﹣1)得x>﹣4,
解不等式5﹣(x+4)≥x,得:x≤2,
∴不等式组的解集为﹣4<x≤2,
在数轴上表示如图.故最小整数解是﹣3.
20.△ABC在平面直角坐标系中的位置如图,现将△ABC先向上平移2个单位再向左平移5个单位得到△A1B1C1.
(1)画出△A1B1C1;
(2)写出点A1、B1、C1的坐标:A1 (﹣1,5) 、B1 (﹣2,3) 、C1 (﹣4,4) ;
(3)求△A1B1C1的面积.
解:(1)如图所示,△A1B1C1即为所求.
(2)由图知,A1 (﹣1,5)、B1 (﹣2,3)、C1(﹣4,4),
故答案为:(﹣1,5),(﹣2,3),(﹣4,4);
(3)△A1B1C1的面积为2×3﹣×1×2﹣×1×2﹣×1×3=.
六、(本题满分12分)
21.某校为了解学生近视情况,随机抽查了部分同学的视力,整理并制作出频数分布表和频数分布直方图(不完整).
请根据图表中提供的信息解答问题:
得分 频数 百分比
4.2≤x<4.4 5 m%
4.4≤x<4.6 15 7.5%
4.6≤x<4.8 60 30%
4.8≤x<5.0 n 45%
5.0≤x<5.2 30 15%
(1)在统计表中,m= 2.5 ,n= 90 ;
(2)补全频数分布直方图;
(3)若制作扇形统计图,则“4.6<x≤4.8”所在扇形的圆心角的度数为 108° ;
(4)该校有2000名学生,请你根据以上抽样调查结果,估计视力5.0以上(包括5.0)的学生有多少人.
解:(1)∵被调查的总人数为15÷7.5%=200(人),
∴m%=×100%=2.5%,即m=2.5;n=200×45%=90,
故答案为:2.5,90;
(2)补全图形如下:
(3)若制作扇形统计图,则“4.6<x≤4.8”所在扇形的圆心角的度数为360°×=108°,
故答案为:108°;
(4)估计视力5.0以上(包括5.0)的学生人数为2000×=300(人).
七、(本题满分12分)
22.学校为了更新教学辅助设备,准备购买若干台电脑和打印机.如果购买1台电脑,2台打印机,需要花费5900元;如果购买2台电脑,2台打印机,需要花费9400元.
(1)求每台电脑和每台打印机的价格分别是多少元?
(2)如果学校购买电脑和打印机的预算费用不超过20000元,并且购买打印机的台数要比购买电脑的台数多1台,那么该学校至多能购买多少台打印机?
解:(1)设每台电脑的价格为x元,每台打印机的价格为y元,
根据题意,得:,
解得:,
答:每台电脑的价格为3500元,每台打印机的价格为1200元;
(2)设学校购买a台打印机,则购买电脑为(a﹣1)台,
根据题意,得:3500(a﹣1)+1200a≤20000,
解得:a≤5,
答:该学校至多能购买5台打印机.
八、(本题满分14分)
23.如图1,AB⊥BC于点B,CD⊥BC于点C,点E在线段BC上,且AE⊥DE.
(1)求证:∠EAB=∠CED;
(2)如图2,AF、DF分别平分∠BAE和∠CDE,则∠F的度数是 45° (直接写出答案即可);
(3)如图3,EH平分∠CED,EH的反向延长线交∠BAE的平分线AF于点G.求证:EG⊥AF.(提示:三角形内角和等于180°)
【解答】(1)证明:∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°,
∴∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠CED=90°,
∴∠BAE=∠CED.
(2)解:答案为45°;
过点F作FM∥AB,如图,
∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°,
∴AB∥CD,
∵∠C=90°,
∴∠CED+∠CDE=90°,
∵∠BAE=∠CED,
∴∠BAE+∠CDE=90°,
∵AF、DF分别平分∠BAE和∠CDE,
∴∠CDF=∠CDE,∠BAF=∠BAE,
∴∠CDF+∠BAF=(∠BAE+∠CDE)=45°,
∵FM∥AB∥CD,
∴∠CDF=∠DFM,∠BAF=∠AFM,
∴∠AFD=∠CDF+∠BAF=45°.
(3)∵EH平分∠CED,
∴∠CEH=∠CED,
∴∠BEG=∠CED,
∵AF平分∠BAE,
∴∠BAG=∠BAE,
∵∠BAE=∠CED,
∴∠BAG=∠BEG,
∵∠BAE+∠BEA=90°,
∴∠BAG+∠GAE+∠AEB=90°,
即∠GAE+∠AEB+∠BEG=90°,
∴∠AGE=90°,
∴EG⊥AF.
一、选择题(每小题4分,满分40分)
1.3的平方根是( )
A.9 B. C.﹣ D.±
2.若是二元一次方程x﹣my+3=0的解,则m的值为( )
A.6 B.4 C.0 D.
3.要了解学校在新冠肺炎防控中的有关情况,下面适合用抽样调查的是( )
①了解各校口罩、洗手液、消毒液的储备情况;
②了解师生在假期的离校情况;
③了解师生入校时的体温情况;
④了解师生对“七步洗手法”的运用情况.
A.① B.② C.③ D.④
4.若a<b,则下列变形错误的是( )
A.2a<2b B.2+a<2+b C.2﹣a<2﹣b D.a<b
5.庐江县是合肥市的南部副中心,以下能准确表示庐江县地理位置的是( )
A.在合肥市区的南部
B.东经117.48°
C.距离合肥79km处
D.东经117.48°北纬31.25°
6.如图,在下列条件中,不能判定直线a与b平行的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠5 D.∠3+∠4=180°
7.《九章算术》中的算筹图是竖排的,为看图方便我们把它改为横排,如图1,图2所示,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.图1表示的算筹图用我们现在所熟悉的方程组形式表述出来为.类似地,图2所示的算筹图我们可以表述为( )
A. B.
C. D.
8.已知某程序如图所示,规定:从“输入实数x”到“结果是否大于95”为一次操作.如果该程序进行了两次操作停止,那么实数x的取值范围是( )
A.x>23 B.11≤x≤23 C.23<x≤47 D.x≤47
9.如图,在平面直角坐标系上有个点P(1,0),点P第1次向上平移1个单位至点P1(1,1),紧接着第2次向左平移2个单位至点P2(﹣1,1),第3次向上平移1个单位到达P3(﹣1,2),第4次向右平移3个单位到达P4(2,2),第5次又向上平移1个单位,第6次向左平移4个单位,…,依此规律平移下去,点P2021的坐标为( )
A.(506,1011) B.(506,﹣506)
C.(﹣506,1011) D.(﹣506,506)
10.如图,直线AB与CD相交于点O,∠DOE=α,∠DOF:∠AOD=2:3,射线OE平分∠BOF,则∠BOC=( )
A.540°﹣5α B.540°﹣6α C.30° D.40°
二、填空题(本题共4小题,每小题5分,满分20分)
11.“对顶角相等”的逆命题是 .(用“如果…那么…”的形式写出)
12.长方形的面积是15,它的长与宽的比为3:1,则该长方形的宽为 .
13.在平面直角坐标系中,AB=2,且AB∥y,若点A的坐标为(2,1),则点B的坐标为 .
14.如图1,将一条对边互相平行的纸条进行两次折叠,第一次折叠的折痕为AB,且∠1=25°,第二次折叠的折痕为CD.
(1)如图2,若CD∥AB,则∠2= .
(2)如图3,若CD∥BE,则∠2= .
三、(本题共2小题,每小题8分,满分16分)
15.计算:+|1﹣|.
16.解方程组.
四、(本题共2小题,每小题8分,满分16分)
17.如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.
(1)求∠ABC的度数;
(2)要使CD∥AB,直接写出D处应在C处的什么方向: .
18.数轴上的点A、B依次表示两个实数.
(1)如图,在数轴上描出点A和点B的大致位置;
(2)如果点C在数轴上,且点C到点A的距离是,求点C所对应的实数.
五、(本题共2小题。每小题10分,满分20分)
19.解不等式组,并将解集在数轴上表示出来,并写出最小整数解.
20.△ABC在平面直角坐标系中的位置如图,现将△ABC先向上平移2个单位再向左平移5个单位得到△A1B1C1.
(1)画出△A1B1C1;
(2)写出点A1、B1、C1的坐标:A1 、B1 、C1 ;
(3)求△A1B1C1的面积.
六、(本题满分12分)
21.某校为了解学生近视情况,随机抽查了部分同学的视力,整理并制作出频数分布表和频数分布直方图(不完整).
请根据图表中提供的信息解答问题:
得分 频数 百分比
4.2≤x<4.4 5 m%
4.4≤x<4.6 15 7.5%
4.6≤x<4.8 60 30%
4.8≤x<5.0 n 45%
5.0≤x<5.2 30 15%
(1)在统计表中,m= ,n= ;
(2)补全频数分布直方图;
(3)若制作扇形统计图,则“4.6<x≤4.8”所在扇形的圆心角的度数为 ;
(4)该校有2000名学生,请你根据以上抽样调查结果,估计视力5.0以上(包括5.0)的学生有多少人.
七、(本题满分12分)
22.学校为了更新教学辅助设备,准备购买若干台电脑和打印机.如果购买1台电脑,2台打印机,需要花费5900元;如果购买2台电脑,2台打印机,需要花费9400元.
(1)求每台电脑和每台打印机的价格分别是多少元?
(2)如果学校购买电脑和打印机的预算费用不超过20000元,并且购买打印机的台数要比购买电脑的台数多1台,那么该学校至多能购买多少台打印机?
八、(本题满分14分)
23.如图1,AB⊥BC于点B,CD⊥BC于点C,点E在线段BC上,且AE⊥DE.
(1)求证:∠EAB=∠CED;
(2)如图2,AF、DF分别平分∠BAE和∠CDE,则∠F的度数是 (直接写出答案即可);
(3)如图3,EH平分∠CED,EH的反向延长线交∠BAE的平分线AF于点G.求证:EG⊥AF.(提示:三角形内角和等于180°)
参考答案
一、选择题(本题共10小题,每小题4分,满分40分。请将每小题唯一正确选项前的代号填入下面的答题栏内)
1.3的平方根是( )
A.9 B. C.﹣ D.±
解:∵()2=3,
∴3的平方根.
故选:D.
2.若是二元一次方程x﹣my+3=0的解,则m的值为( )
A.6 B.4 C.0 D.
解:将代入x﹣my+3=0中,可得3﹣m+3=0,
∴m=6,
故选:A.
3.要了解学校在新冠肺炎防控中的有关情况,下面适合用抽样调查的是( )
①了解各校口罩、洗手液、消毒液的储备情况;
②了解师生在假期的离校情况;
③了解师生入校时的体温情况;
④了解师生对“七步洗手法”的运用情况.
A.① B.② C.③ D.④
解:①了解各校口罩、洗手液、消毒液的储备情况,适宜采用全面调查;
②了解师生在假期的离校情况,适宜采用全面调查;
③了解师生入校时的体温情况,适宜采用全面调查;
④了解师生对“七步洗手法”的运用情况,适合用抽样调查;
故选:D.
4.若a<b,则下列变形错误的是( )
A.2a<2b B.2+a<2+b C.2﹣a<2﹣b D.a<b
解:∵a<b,
∴2a<2b,2+a<2+b,﹣a>﹣b,a<b,
∴2﹣a>2﹣b,
故选:C.
5.庐江县是合肥市的南部副中心,以下能准确表示庐江县地理位置的是( )
A.在合肥市区的南部
B.东经117.48°
C.距离合肥79km处
D.东经117.48°北纬31.25°
解:A、在合肥市区的南部,无法准确确定庐江县地理位置,不符合题意;
B、东经117.48°,无法准确确定庐江县地理位置,不符合题意;
C、距离合肥79km处,无法准确确定长沙地理位置无法准确确定庐江县地理位置,不符合题意;
D、东经117.48°北纬31.25°,是地球上唯一的点,能准确表示庐江县地理位置,符合题意;
故选:D.
6.如图,在下列条件中,不能判定直线a与b平行的是( )
A.∠1=∠2 B.∠2=∠3 C.∠1=∠5 D.∠3+∠4=180°
解:A、∵∠1=∠2,∴a∥b,不符合题意;
B、∵∠2=∠3,∴a∥b,不符合题意;
C、∵∠1与∠5既不是直线a,b被任何一条直线所截的一组同位角,内错角,
∴∠1=∠5,不能得到a∥b,
∴符合题意;
D、∵∠3+∠4=180°,∴a∥b,不符合题意;
故选:C.
7.《九章算术》中的算筹图是竖排的,为看图方便我们把它改为横排,如图1,图2所示,图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.图1表示的算筹图用我们现在所熟悉的方程组形式表述出来为.类似地,图2所示的算筹图我们可以表述为( )
A. B.
C. D.
解:图2所示的算筹图我们可以表述为:.
故选:C.
8.已知某程序如图所示,规定:从“输入实数x”到“结果是否大于95”为一次操作.如果该程序进行了两次操作停止,那么实数x的取值范围是( )
A.x>23 B.11≤x≤23 C.23<x≤47 D.x≤47
解:第一次的结果为:2x+1,没有输出,则2x+1≤95,
解得:x≤47;
第二次的结果为:2(2x+1)+1=4x+3,输出,则4x+3>95,
解得:x>23;
综上可得:23<x≤47.
故选:C.
9.如图,在平面直角坐标系上有个点P(1,0),点P第1次向上平移1个单位至点P1(1,1),紧接着第2次向左平移2个单位至点P2(﹣1,1),第3次向上平移1个单位到达P3(﹣1,2),第4次向右平移3个单位到达P4(2,2),第5次又向上平移1个单位,第6次向左平移4个单位,…,依此规律平移下去,点P2021的坐标为( )
A.(506,1011) B.(506,﹣506)
C.(﹣506,1011) D.(﹣506,506)
解:设第n次跳动至点Pn,
观察发现:P(1,0),P1(1,1),P2(﹣1,1),P3(﹣1,2),P4(2,2),P5(2,3),P6(﹣2,3),P7(﹣2,4),P8(3,4),P9(3,5),…,
∴P4n(n+1,2n),P4n+1(n+1,2n+1),P4n+2(﹣n﹣1,2n+1),P4n+3(﹣n﹣1,2n+2)(n为自然数).
∵2021=505×4+1,
∴P2021(505+1,505×2+1),即(506,1011).
故选:A.
10.如图,直线AB与CD相交于点O,∠DOE=α,∠DOF:∠AOD=2:3,射线OE平分∠BOF,则∠BOC=( )
A.540°﹣5α B.540°﹣6α C.30° D.40°
解:设∠DOF=2x,∠AOD=3x,
∵∠DOE=α,
∴∠FOE=α﹣2x,
∵射线OE平分∠BOF,
∴∠BOE=∠EOF=α﹣2x,
则:3x+α+α﹣2x=180°,
解得:x=180°﹣2α,
∴∠AOD=3×(180°﹣2α)=540°﹣6α,
∴∠BOC=540°﹣6α,
故选:B.
二、填空题(本题共4小题,每小题5分,满分20分)
11.“对顶角相等”的逆命题是 如果两个角相等,那么这两个角是对顶角 .(用“如果…那么…”的形式写出)
解:命题“对顶角相等.”的逆命题:如果两个角相等,那么这两个角是对顶角,
故答案为:如果两个角相等,那么这两个角是对顶角.
12.长方形的面积是15,它的长与宽的比为3:1,则该长方形的宽为 .
解:设矩形的宽为x,则长为3x,
根据题意得:3x2=15,
所以x2=5.
解得:x=±(负值舍去),
∴长方形的宽为,
故答案为:.
13.在平面直角坐标系中,AB=2,且AB∥y,若点A的坐标为(2,1),则点B的坐标为 (2,﹣1)或(2,3) .
解:∵在平面直角坐标系中,AB=2,且AB∥y,若点A的坐标为(2,1),
∴点B的坐标为(2,﹣1)或(2,3).
故答案为:(2,﹣1)或(2,3).
14.如图1,将一条对边互相平行的纸条进行两次折叠,第一次折叠的折痕为AB,且∠1=25°,第二次折叠的折痕为CD.
(1)如图2,若CD∥AB,则∠2= 25° .
(2)如图3,若CD∥BE,则∠2= 80° .
解:(1)如图2,
∵CD∥AB,
∴∠1+∠ACD=180°,
∵∠1=25°,
∴∠ACD=180°﹣25°=155°,
∵AC∥BD,
∴∠ACD+∠2=180°,
∴∠2=180°﹣∠ACD=25°,
故答案为:25°;
(2)如图3,由折叠的性质,可得∠3=∠1=25°,
∵EB∥AM,
∴∠4=∠1+∠3=50°,
∵AC∥BD,
∴∠4+∠EBD=180°,
∴∠EBD=180°﹣∠4=130°,
又∵CD∥BE,
∴∠EBD+∠BDC=180°,
∴∠BDC=50°,
由折叠的性质,可得2∠BDC+∠2=180°,
∴∠2=180°﹣100°=80°,
故答案为:80°.
三、(本题共2小题,每小题8分,满分16分)
15.计算:+|1﹣|.
解:+|1﹣|
=2+(﹣2)+﹣1
=﹣1.
16.解方程组.
解:,
把②代入①,得2(1﹣y)+4y=5,
解得:y=,把y=代入②,得x=1﹣=﹣,
所以方程组的解是.
四、(本题共2小题,每小题8分,满分16分)
17.如图,B处在A处的南偏西45°方向,C处在B处的北偏东80°方向.
(1)求∠ABC的度数;
(2)要使CD∥AB,直接写出D处应在C处的什么方向: D在C的南偏西45° .
解:(1)如图,由题意得∠FAB=45°,
∵AF∥BE,
∴∠FAB=∠ABE=45°,
∵∠EBC=80°
∴∠ABC=35°;
(2)D在C的南偏西45°,理由如下:
∵CG∥BE,
∴∠GCB=∠EBC=80°,
∵∠GCD=45°
∴∠BCD=35°
∴∠ABC=∠BCD=35°,
∴CD∥AB.
故答案为:D在C的南偏西45°.
18.数轴上的点A、B依次表示两个实数.
(1)如图,在数轴上描出点A和点B的大致位置;
(2)如果点C在数轴上,且点C到点A的距离是,求点C所对应的实数.
解:(1)如图:
(2)设点C表示的数是x,则:
|x+|=2.
∴x=或﹣3.
∴点C表示的数是或﹣3.
五、(本题共2小题。每小题10分,满分20分)
19.解不等式组,并将解集在数轴上表示出来,并写出最小整数解.
解:解不等式2x<7(x﹣1)得x>﹣4,
解不等式5﹣(x+4)≥x,得:x≤2,
∴不等式组的解集为﹣4<x≤2,
在数轴上表示如图.故最小整数解是﹣3.
20.△ABC在平面直角坐标系中的位置如图,现将△ABC先向上平移2个单位再向左平移5个单位得到△A1B1C1.
(1)画出△A1B1C1;
(2)写出点A1、B1、C1的坐标:A1 (﹣1,5) 、B1 (﹣2,3) 、C1 (﹣4,4) ;
(3)求△A1B1C1的面积.
解:(1)如图所示,△A1B1C1即为所求.
(2)由图知,A1 (﹣1,5)、B1 (﹣2,3)、C1(﹣4,4),
故答案为:(﹣1,5),(﹣2,3),(﹣4,4);
(3)△A1B1C1的面积为2×3﹣×1×2﹣×1×2﹣×1×3=.
六、(本题满分12分)
21.某校为了解学生近视情况,随机抽查了部分同学的视力,整理并制作出频数分布表和频数分布直方图(不完整).
请根据图表中提供的信息解答问题:
得分 频数 百分比
4.2≤x<4.4 5 m%
4.4≤x<4.6 15 7.5%
4.6≤x<4.8 60 30%
4.8≤x<5.0 n 45%
5.0≤x<5.2 30 15%
(1)在统计表中,m= 2.5 ,n= 90 ;
(2)补全频数分布直方图;
(3)若制作扇形统计图,则“4.6<x≤4.8”所在扇形的圆心角的度数为 108° ;
(4)该校有2000名学生,请你根据以上抽样调查结果,估计视力5.0以上(包括5.0)的学生有多少人.
解:(1)∵被调查的总人数为15÷7.5%=200(人),
∴m%=×100%=2.5%,即m=2.5;n=200×45%=90,
故答案为:2.5,90;
(2)补全图形如下:
(3)若制作扇形统计图,则“4.6<x≤4.8”所在扇形的圆心角的度数为360°×=108°,
故答案为:108°;
(4)估计视力5.0以上(包括5.0)的学生人数为2000×=300(人).
七、(本题满分12分)
22.学校为了更新教学辅助设备,准备购买若干台电脑和打印机.如果购买1台电脑,2台打印机,需要花费5900元;如果购买2台电脑,2台打印机,需要花费9400元.
(1)求每台电脑和每台打印机的价格分别是多少元?
(2)如果学校购买电脑和打印机的预算费用不超过20000元,并且购买打印机的台数要比购买电脑的台数多1台,那么该学校至多能购买多少台打印机?
解:(1)设每台电脑的价格为x元,每台打印机的价格为y元,
根据题意,得:,
解得:,
答:每台电脑的价格为3500元,每台打印机的价格为1200元;
(2)设学校购买a台打印机,则购买电脑为(a﹣1)台,
根据题意,得:3500(a﹣1)+1200a≤20000,
解得:a≤5,
答:该学校至多能购买5台打印机.
八、(本题满分14分)
23.如图1,AB⊥BC于点B,CD⊥BC于点C,点E在线段BC上,且AE⊥DE.
(1)求证:∠EAB=∠CED;
(2)如图2,AF、DF分别平分∠BAE和∠CDE,则∠F的度数是 45° (直接写出答案即可);
(3)如图3,EH平分∠CED,EH的反向延长线交∠BAE的平分线AF于点G.求证:EG⊥AF.(提示:三角形内角和等于180°)
【解答】(1)证明:∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°,
∴∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠CED=90°,
∴∠BAE=∠CED.
(2)解:答案为45°;
过点F作FM∥AB,如图,
∵AB⊥BC,CD⊥BC,
∴∠B=∠C=90°,
∴AB∥CD,
∵∠C=90°,
∴∠CED+∠CDE=90°,
∵∠BAE=∠CED,
∴∠BAE+∠CDE=90°,
∵AF、DF分别平分∠BAE和∠CDE,
∴∠CDF=∠CDE,∠BAF=∠BAE,
∴∠CDF+∠BAF=(∠BAE+∠CDE)=45°,
∵FM∥AB∥CD,
∴∠CDF=∠DFM,∠BAF=∠AFM,
∴∠AFD=∠CDF+∠BAF=45°.
(3)∵EH平分∠CED,
∴∠CEH=∠CED,
∴∠BEG=∠CED,
∵AF平分∠BAE,
∴∠BAG=∠BAE,
∵∠BAE=∠CED,
∴∠BAG=∠BEG,
∵∠BAE+∠BEA=90°,
∴∠BAG+∠GAE+∠AEB=90°,
即∠GAE+∠AEB+∠BEG=90°,
∴∠AGE=90°,
∴EG⊥AF.
同课章节目录
