数学:1.5 中位线 课件1(苏科版九上)
文档属性
| 名称 | 数学:1.5 中位线 课件1(苏科版九上) |  | |
| 格式 | zip | ||
| 文件大小 | 150.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-16 22:24:32 | ||
图片预览


文档简介
(共18张PPT)
A
B
C
D
E
F
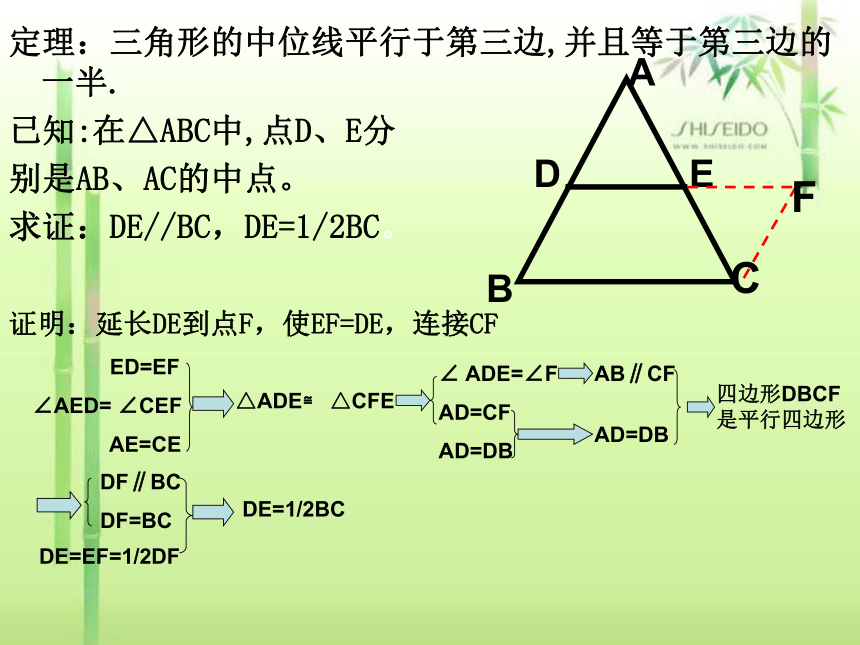
定理:三角形的中位线平行于第三边,并且等于第三边的一半.
已知:在△ABC中,点D、E分
别是AB、AC的中点。
求证:DE//BC,DE=1/2BC。
证明:延长DE到点F,使EF=DE,连接CF
A
B
C
D
E
F
ED=EF
∠AED= ∠CEF
AE=CE
△ADE≌ △CFE
∠ ADE=∠F
AD=CF
AD=DB
AD=DB
AB∥CF
四边形DBCF是平行四边形
DF∥BC
DF=BC
DE=EF=1/2DF
DE=1/2BC
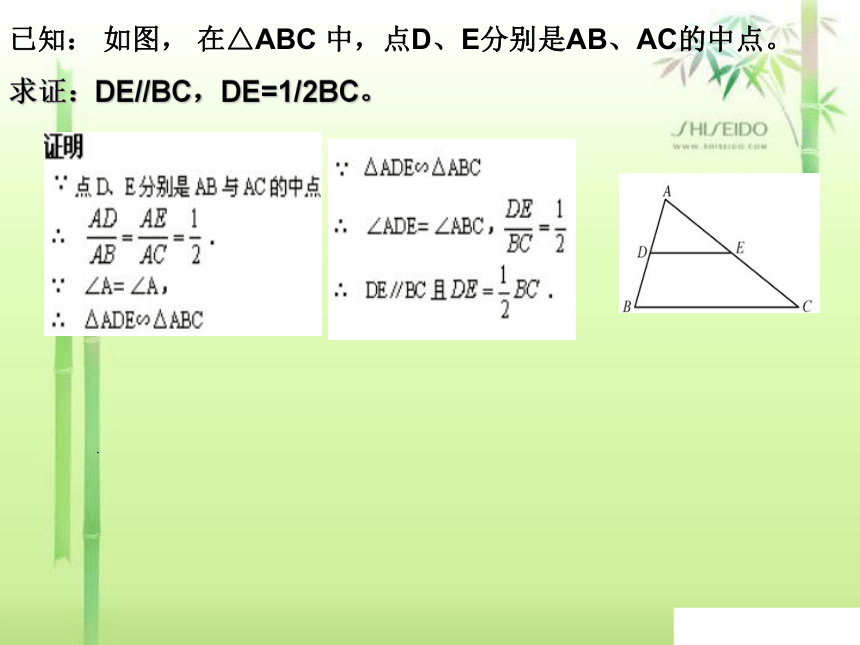
已知: 如图, 在△ABC 中,点D、E分别是AB、AC的中点。
求证:DE//BC,DE=1/2BC。
.
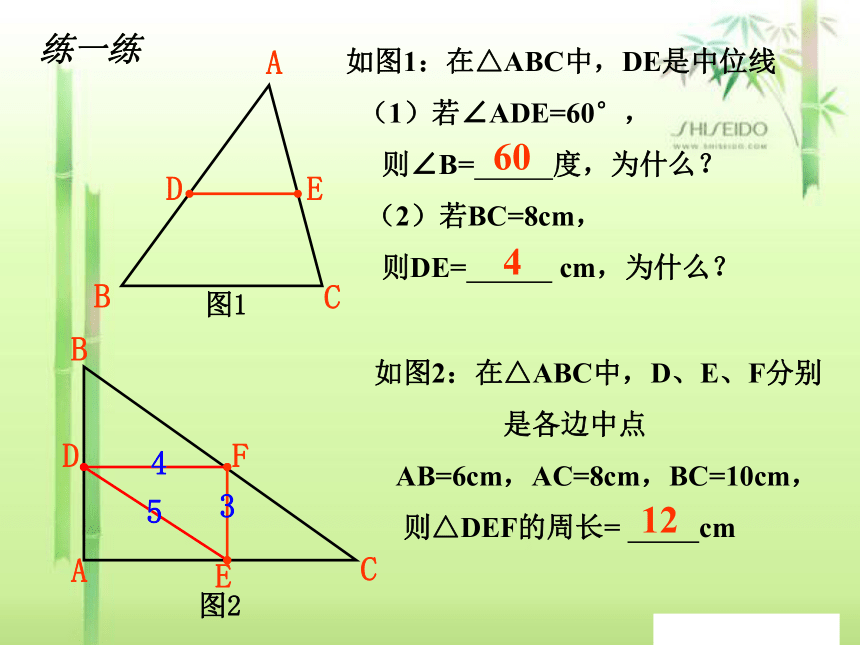
如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么?
如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm
图1
图2
60
4
12
A
B
C
D
E
B
A
C
D
E
F
5
4
3
练一练
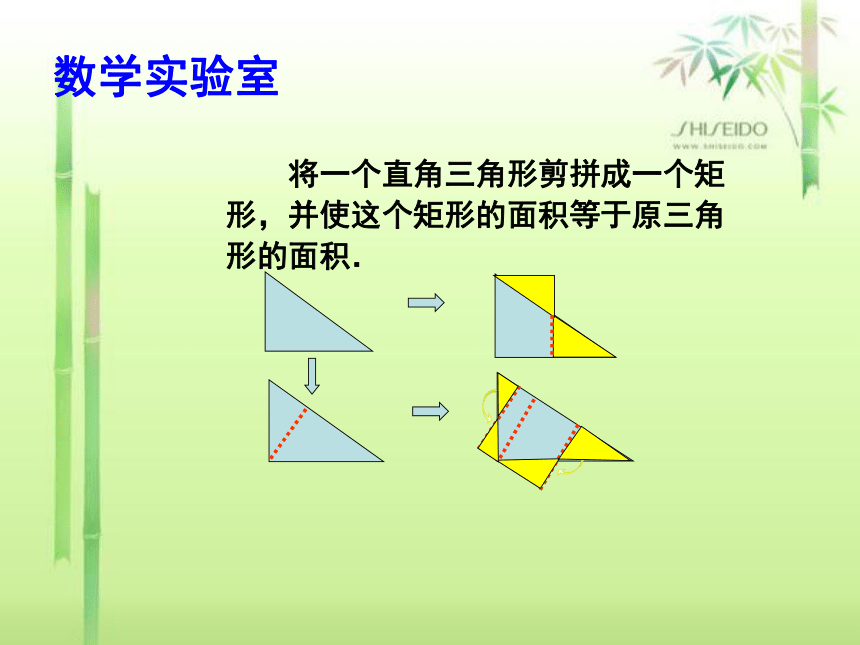
将一个直角三角形剪拼成一个矩形,并使这个矩形的面积等于原三角
形的面积.
数学实验室
将一个直角三角形剪拼成一个矩形,并使这个矩形的面积等于原三角
形的面积.
数学实验室
A
B
C
D
E
F
G
H
通过以上的剪拼活动,你还能找到证明三角形中位线定理的其他方法吗
如果是一个非直角三角形呢
例1:已知:如图,在梯形ABCD中,AD//BC,E、F分别是AB、DC的中点。
求证:EF//BC,且EF=1/2(BC+AD)
E
B
C
D
A
F
G
证明:连接AF并延长,交BC的延长线于点G
∵ AD//BC ∴∠D=∠FCG
在△ADF和△GCF中
∠D=∠FCG
DF=CF
∠AFD=∠GFC
∴ △ADF≌△GCF(ASA)
∴AF=GF,AD=GC
∵AE=EB
∴EF是△ABG的中位线
∴ EF//BC,EF=1/2BG=1/2(BC+CG)
∵AD=GC
∴ EF=1/2(BC+AD)
A
B
C
D
E
F
M
N
证明:过点F作MN∥AB,交AD的延长线于点M,交BC于点N.
∵AD∥BC,
∴四边形AMNB是平行
四边形,且∠MDF=∠FCN.
∴AB=MN.
在△DFM和△CFN中,
∠MDF=∠FCN ,
DF=CF ,
∠DFM=∠CFN ,
∴△DFM≌△CFN(ASA).
∴DM=CN,MF=FN=1/2 MN.
又∵AE=EB=1/2 AB.
∴AE=EB=MF=FN.
∴四边形AEFM,EBNF是平行四边形.
∴AM=EF=BC,
EF∥BC∥AD.
∴ EF=1/2 (AD+BC).
归纳与概括:
你能仿照三角形中位线定理,用文字语言来概括
梯形中位线的性质吗
A
B
C
D
E
F
类比与思考
梯形中位线的性质与三角形中位线定理有什么联系
类比与思考
(1)都有“平行”和“一半”两大特点;
(2)当AD的长度为0时,梯形中位线就变成了三角形中位线.
已知△ABC,分别连接三边中点D,E,F(如图),
你能得到哪些结论呢
A
B
C
D
E
F
我们可以从线段的数量关系、三角形是否全等、是否有平行四边形等不同的角度来寻找.
连接AF,你有什么发现呢
若请你添加一个条件,你又有什么发现呢
一试身手
如图,A,B两地被建筑物阻隔,为测量A,B两地间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB
的中点D,E.
B
E
D
B
A
C
(1)如果DE的长
为36 m,求A,B两地
间的距离;
(2)如果D,E两点间还有障碍物阻隔,你该如何解决
已知:在四边形ABCD中,AB=CD,E、F、G分别是BD、AC、BC的中点。
求证:△EFG是等腰三角形。
A
B
C
D
E
F
G
证明:∵E、G分别是BD、BC的中点
∴EG是△BCD的中位线
∴EG=1/2AB
∵ F、G分别是AC、BC的中点
∴FG是△ABC的中位线
∴FG=1/2AB
∵ AB=CD
∴EG=FG
∴ △EFG是等腰三角形
剪拼三角形
三角形中位线定理
梯形中位线性质
1.
2.从实验操作中发现添加辅助线的方法.
3.转化思想的应用——将三角形问题转化为平行四边形问题,
将梯形中位线问题转化为三角形中位线.
小明有一个解不开的迷:他任意画了三个△ABC(不全等),
发现只要向图中的角平分线BG、CF作垂线AG、AF,连接两
垂足F、G,则FG总是与BC平行,但他不会证明,你能解开
这个迷吗?
M
N
A
B
C
D
E
F
定理:三角形的中位线平行于第三边,并且等于第三边的一半.
已知:在△ABC中,点D、E分
别是AB、AC的中点。
求证:DE//BC,DE=1/2BC。
证明:延长DE到点F,使EF=DE,连接CF
A
B
C
D
E
F
ED=EF
∠AED= ∠CEF
AE=CE
△ADE≌ △CFE
∠ ADE=∠F
AD=CF
AD=DB
AD=DB
AB∥CF
四边形DBCF是平行四边形
DF∥BC
DF=BC
DE=EF=1/2DF
DE=1/2BC
已知: 如图, 在△ABC 中,点D、E分别是AB、AC的中点。
求证:DE//BC,DE=1/2BC。
.
如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B= 度,为什么?
(2)若BC=8cm,
则DE= cm,为什么?
如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长= cm
图1
图2
60
4
12
A
B
C
D
E
B
A
C
D
E
F
5
4
3
练一练
将一个直角三角形剪拼成一个矩形,并使这个矩形的面积等于原三角
形的面积.
数学实验室
将一个直角三角形剪拼成一个矩形,并使这个矩形的面积等于原三角
形的面积.
数学实验室
A
B
C
D
E
F
G
H
通过以上的剪拼活动,你还能找到证明三角形中位线定理的其他方法吗
如果是一个非直角三角形呢
例1:已知:如图,在梯形ABCD中,AD//BC,E、F分别是AB、DC的中点。
求证:EF//BC,且EF=1/2(BC+AD)
E
B
C
D
A
F
G
证明:连接AF并延长,交BC的延长线于点G
∵ AD//BC ∴∠D=∠FCG
在△ADF和△GCF中
∠D=∠FCG
DF=CF
∠AFD=∠GFC
∴ △ADF≌△GCF(ASA)
∴AF=GF,AD=GC
∵AE=EB
∴EF是△ABG的中位线
∴ EF//BC,EF=1/2BG=1/2(BC+CG)
∵AD=GC
∴ EF=1/2(BC+AD)
A
B
C
D
E
F
M
N
证明:过点F作MN∥AB,交AD的延长线于点M,交BC于点N.
∵AD∥BC,
∴四边形AMNB是平行
四边形,且∠MDF=∠FCN.
∴AB=MN.
在△DFM和△CFN中,
∠MDF=∠FCN ,
DF=CF ,
∠DFM=∠CFN ,
∴△DFM≌△CFN(ASA).
∴DM=CN,MF=FN=1/2 MN.
又∵AE=EB=1/2 AB.
∴AE=EB=MF=FN.
∴四边形AEFM,EBNF是平行四边形.
∴AM=EF=BC,
EF∥BC∥AD.
∴ EF=1/2 (AD+BC).
归纳与概括:
你能仿照三角形中位线定理,用文字语言来概括
梯形中位线的性质吗
A
B
C
D
E
F
类比与思考
梯形中位线的性质与三角形中位线定理有什么联系
类比与思考
(1)都有“平行”和“一半”两大特点;
(2)当AD的长度为0时,梯形中位线就变成了三角形中位线.
已知△ABC,分别连接三边中点D,E,F(如图),
你能得到哪些结论呢
A
B
C
D
E
F
我们可以从线段的数量关系、三角形是否全等、是否有平行四边形等不同的角度来寻找.
连接AF,你有什么发现呢
若请你添加一个条件,你又有什么发现呢
一试身手
如图,A,B两地被建筑物阻隔,为测量A,B两地间的距离,在地面上选一点C,连接CA,CB,分别取CA,CB
的中点D,E.
B
E
D
B
A
C
(1)如果DE的长
为36 m,求A,B两地
间的距离;
(2)如果D,E两点间还有障碍物阻隔,你该如何解决
已知:在四边形ABCD中,AB=CD,E、F、G分别是BD、AC、BC的中点。
求证:△EFG是等腰三角形。
A
B
C
D
E
F
G
证明:∵E、G分别是BD、BC的中点
∴EG是△BCD的中位线
∴EG=1/2AB
∵ F、G分别是AC、BC的中点
∴FG是△ABC的中位线
∴FG=1/2AB
∵ AB=CD
∴EG=FG
∴ △EFG是等腰三角形
剪拼三角形
三角形中位线定理
梯形中位线性质
1.
2.从实验操作中发现添加辅助线的方法.
3.转化思想的应用——将三角形问题转化为平行四边形问题,
将梯形中位线问题转化为三角形中位线.
小明有一个解不开的迷:他任意画了三个△ABC(不全等),
发现只要向图中的角平分线BG、CF作垂线AG、AF,连接两
垂足F、G,则FG总是与BC平行,但他不会证明,你能解开
这个迷吗?
M
N
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
