12.2第4课时 利用斜边、直角边判定直角三角形全等(HL) 2021--2022学年人教版八年级数学上册(word版含答案)
文档属性
| 名称 | 12.2第4课时 利用斜边、直角边判定直角三角形全等(HL) 2021--2022学年人教版八年级数学上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 156.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 11:10:21 | ||
图片预览

文档简介
第4课时 利用斜边、直角边判定直角三角形全等(HL)
知识点1 用“HL”判定直角三角形全等
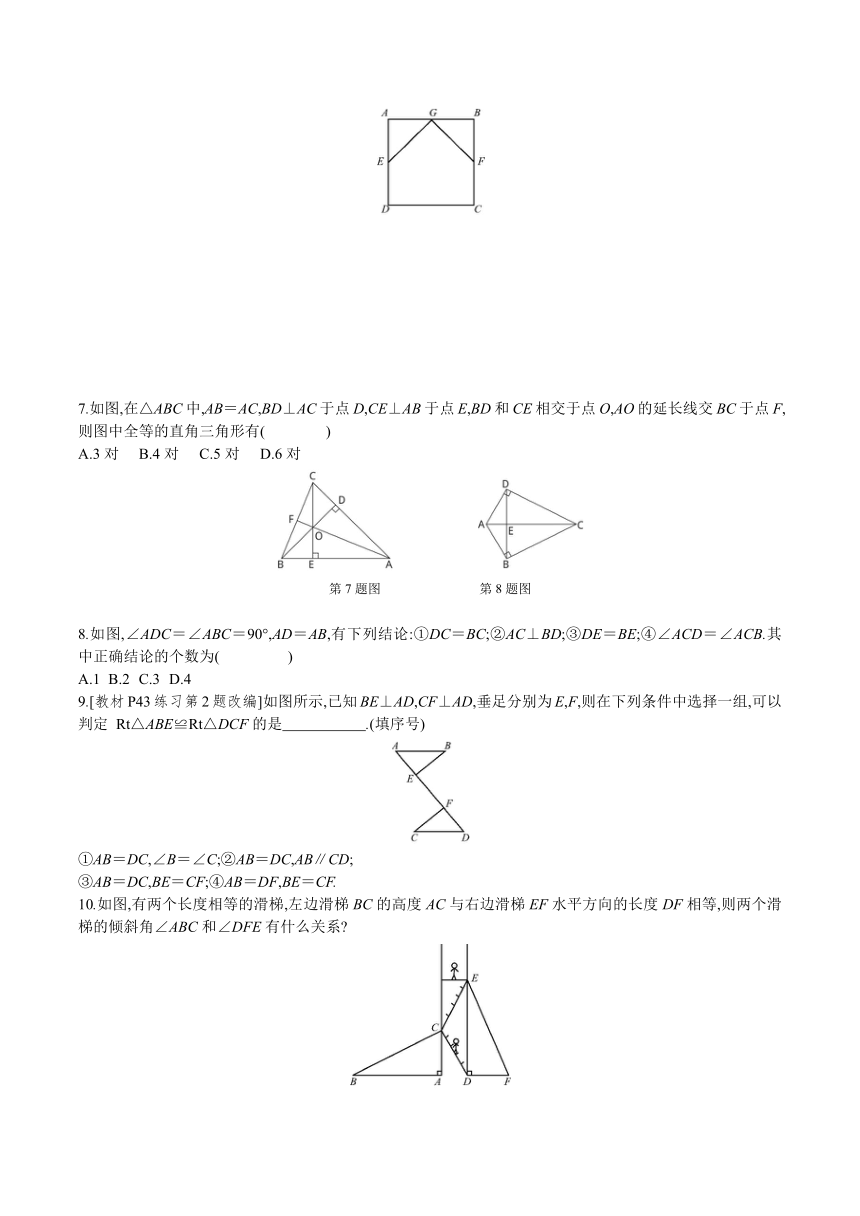
1.如图,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是(
)
A.SSS
B.ASA
C.SAS
D.HL
第1题图
第2题图
2.[教材P42例5改编]如图,在△ABC和△BAD中,已知∠C=∠D=90°,再添加一个条件,就可以用“HL”判定Rt△ABC≌Rt△BAD,你添加的条件是
.?
3.如图,在△ABC中,M是BC的中点,ME⊥AB,MF⊥AC,垂足分别为E,F,ME=MF.求证:△BEM≌△CFM.
知识点2 直角三角形全等的应用
4.如图,已知∠B=∠D=90°,BC=CD,∠1=40°,则∠2的度数为(
)
A.40°
B.50°
C.60°
D.75°
第4题图
第5题图
5.如图,小明和小芳以相同的速度同时分别从点A,B出发,小明沿AC行走,小芳沿BD行走,并且同时到达点C,D.若CB⊥AB,DA⊥AB,则CB
DA.(填“>”“<”或“=”)?
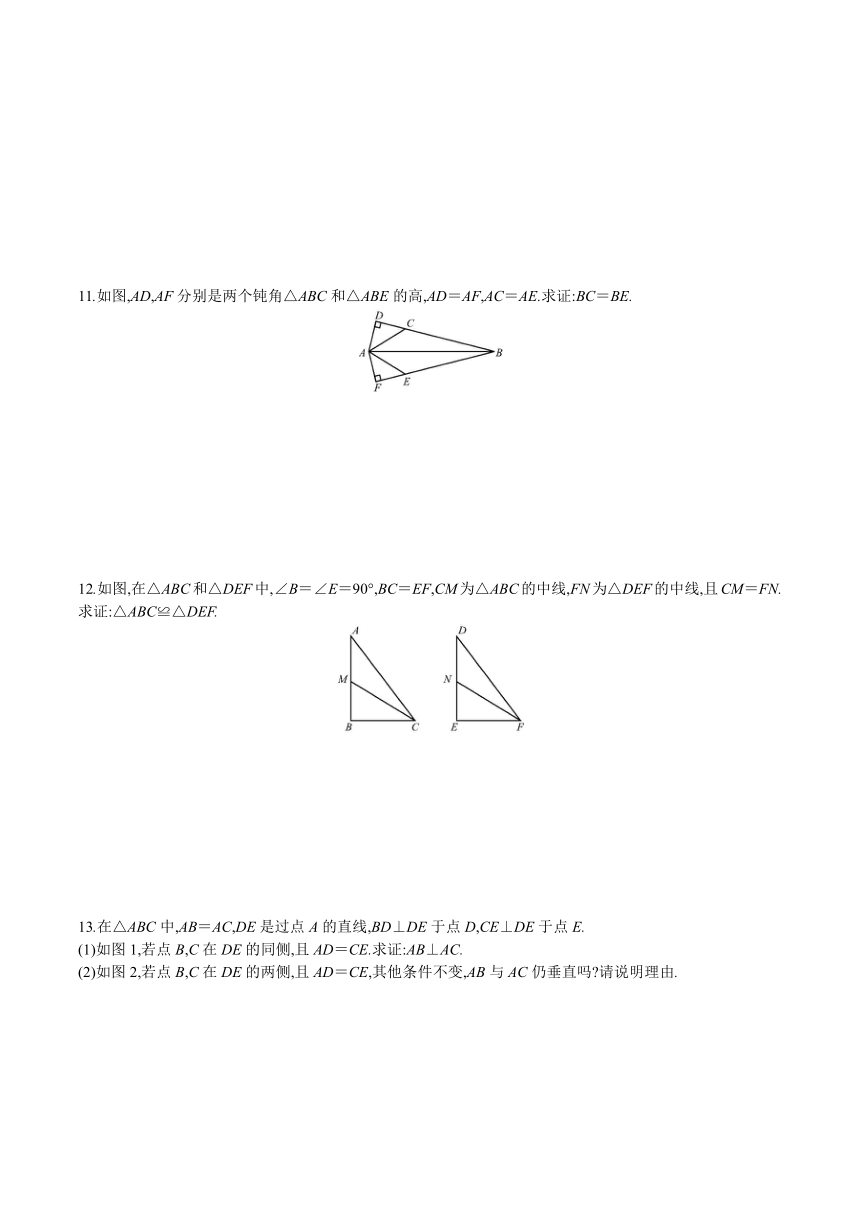
6.如图,工人师傅制作了一个正方形窗架,把窗架立在墙上之前,在上面钉了两根等长的木条GF与GE,E,F分别是AD,BC的中点.
(1)G一定是AB的中点吗?说明理由.
(2)钉这两根木条的作用是什么?
7.如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD和CE相交于点O,AO的延长线交BC于点F,则图中全等的直角三角形有(
)
A.3对
B.4对
C.5对
D.6对
第7题图
第8题图
8.如图,∠ADC=∠ABC=90°,AD=AB,有下列结论:①DC=BC;②AC⊥BD;③DE=BE;④∠ACD=∠ACB.其中正确结论的个数为(
)
A.1
B.2
C.3
D.4
9.[教材P43练习第2题改编]如图所示,已知BE⊥AD,CF⊥AD,垂足分别为E,F,则在下列条件中选择一组,可以判定
Rt△ABE≌Rt△DCF的是
.(填序号)?
①AB=DC,∠B=∠C;②AB=DC,AB∥CD;
③AB=DC,BE=CF;④AB=DF,BE=CF.
10.如图,有两个长度相等的滑梯,左边滑梯BC的高度AC与右边滑梯EF水平方向的长度DF相等,则两个滑梯的倾斜角∠ABC和∠DFE有什么关系?
11.如图,AD,AF分别是两个钝角△ABC和△ABE的高,AD=AF,AC=AE.求证:BC=BE.
12.如图,在△ABC和△DEF中,∠B=∠E=90°,BC=EF,CM为△ABC的中线,FN为△DEF的中线,且CM=FN.求证:△ABC≌△DEF.
13.在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
(1)如图1,若点B,C在DE的同侧,且AD=CE.求证:AB⊥AC.
(2)如图2,若点B,C在DE的两侧,且AD=CE,其他条件不变,AB与AC仍垂直吗?请说明理由.
第4课时 利用斜边、直角边判定直角三角形全等(HL)
知识点1 用“HL”判定直角三角形全等
1.如图,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是(
D
)
A.SSS
B.ASA
C.SAS
D.HL
第1题图
第2题图
2.[教材P42例5改编]如图,在△ABC和△BAD中,已知∠C=∠D=90°,再添加一个条件,就可以用“HL”判定Rt△ABC≌Rt△BAD,你添加的条件是 AC=BD(或AD=BC) .?
3.如图,在△ABC中,M是BC的中点,ME⊥AB,MF⊥AC,垂足分别为E,F,ME=MF.求证:△BEM≌△CFM.
证明:∵M是BC的中点,∴BM=CM.
∵ME⊥AB,MF⊥AC,∴∠BEM=∠CFM=90°.
在Rt△BEM和Rt△CFM中,
∴Rt△BEM≌Rt△CFM(HL).
知识点2 直角三角形全等的应用
4.如图,已知∠B=∠D=90°,BC=CD,∠1=40°,则∠2的度数为(
B
)
A.40°
B.50°
C.60°
D.75°
第4题图
第5题图
5.如图,小明和小芳以相同的速度同时分别从点A,B出发,小明沿AC行走,小芳沿BD行走,并且同时到达点C,D.若CB⊥AB,DA⊥AB,则CB = DA.(填“>”“<”或“=”)?
6.如图,工人师傅制作了一个正方形窗架,把窗架立在墙上之前,在上面钉了两根等长的木条GF与GE,E,F分别是AD,BC的中点.
(1)G一定是AB的中点吗?说明理由.
(2)钉这两根木条的作用是什么?
解:(1)G一定是AB的中点,
理由:在正方形ABCD中,AD=BC,∠A=∠B=90°,
∵E,F分别是AD,BC的中点,∴AE=BF.
在Rt△AEG和Rt△BFG中,
∴△AEG≌△BFG(HL),∴AG=BG,
∴G一定是AB的中点.
(2)结合图形可知,利用三角形的稳定性,使窗架更稳固.
7.如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD和CE相交于点O,AO的延长线交BC于点F,则图中全等的直角三角形有(
D
)
A.3对
B.4对
C.5对
D.6对
第7题图
第8题图
8.如图,∠ADC=∠ABC=90°,AD=AB,有下列结论:①DC=BC;②AC⊥BD;③DE=BE;④∠ACD=∠ACB.其中正确结论的个数为(
D
)
A.1
B.2
C.3
D.4
9.[教材P43练习第2题改编]如图所示,已知BE⊥AD,CF⊥AD,垂足分别为E,F,则在下列条件中选择一组,可以判定
Rt△ABE≌Rt△DCF的是 ①②③ .(填序号)?
①AB=DC,∠B=∠C;②AB=DC,AB∥CD;
③AB=DC,BE=CF;④AB=DF,BE=CF.
10.如图,有两个长度相等的滑梯,左边滑梯BC的高度AC与右边滑梯EF水平方向的长度DF相等,则两个滑梯的倾斜角∠ABC和∠DFE有什么关系?
解:∠ABC与∠DFE互余.
理由:在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ABC=∠DEF.
又∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°,
即两个滑梯的倾斜角∠ABC与∠DFE互余.
11.如图,AD,AF分别是两个钝角△ABC和△ABE的高,AD=AF,AC=AE.求证:BC=BE.
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL),∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL),
∴BD=BF,∴BD-CD=BF-EF,即BC=BE.
12.如图,在△ABC和△DEF中,∠B=∠E=90°,BC=EF,CM为△ABC的中线,FN为△DEF的中线,且CM=FN.求证:△ABC≌△DEF.
证明:在Rt△BCM和Rt△EFN中,
∴Rt△BCM≌Rt△EFN(HL),∴BM=EN.
∵CM为△ABC的中线,FN为△DEF的中线,∴AB=DE.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS).
13.在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
(1)如图1,若点B,C在DE的同侧,且AD=CE.求证:AB⊥AC.
(2)如图2,若点B,C在DE的两侧,且AD=CE,其他条件不变,AB与AC仍垂直吗?请说明理由.
解:(1)∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°.
易证Rt△ABD≌Rt△CAE,∴∠DAB=∠ECA.
∵∠ECA+∠EAC=90°,∴∠DAB+∠EAC=90°,
∴∠BAC=180°-(∠DAB+∠EAC)=90°,
∴AB⊥AC.
(2)AB⊥AC.
理由:易证Rt△ABD≌Rt△CAE,∴∠DAB=∠ECA.
∵∠CAE+∠ECA=90°,∴∠CAE+∠DAB=90°,
即∠BAC=90°,∴AB⊥AC.
知识点1 用“HL”判定直角三角形全等
1.如图,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是(
)
A.SSS
B.ASA
C.SAS
D.HL
第1题图
第2题图
2.[教材P42例5改编]如图,在△ABC和△BAD中,已知∠C=∠D=90°,再添加一个条件,就可以用“HL”判定Rt△ABC≌Rt△BAD,你添加的条件是
.?
3.如图,在△ABC中,M是BC的中点,ME⊥AB,MF⊥AC,垂足分别为E,F,ME=MF.求证:△BEM≌△CFM.
知识点2 直角三角形全等的应用
4.如图,已知∠B=∠D=90°,BC=CD,∠1=40°,则∠2的度数为(
)
A.40°
B.50°
C.60°
D.75°
第4题图
第5题图
5.如图,小明和小芳以相同的速度同时分别从点A,B出发,小明沿AC行走,小芳沿BD行走,并且同时到达点C,D.若CB⊥AB,DA⊥AB,则CB
DA.(填“>”“<”或“=”)?
6.如图,工人师傅制作了一个正方形窗架,把窗架立在墙上之前,在上面钉了两根等长的木条GF与GE,E,F分别是AD,BC的中点.
(1)G一定是AB的中点吗?说明理由.
(2)钉这两根木条的作用是什么?
7.如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD和CE相交于点O,AO的延长线交BC于点F,则图中全等的直角三角形有(
)
A.3对
B.4对
C.5对
D.6对
第7题图
第8题图
8.如图,∠ADC=∠ABC=90°,AD=AB,有下列结论:①DC=BC;②AC⊥BD;③DE=BE;④∠ACD=∠ACB.其中正确结论的个数为(
)
A.1
B.2
C.3
D.4
9.[教材P43练习第2题改编]如图所示,已知BE⊥AD,CF⊥AD,垂足分别为E,F,则在下列条件中选择一组,可以判定
Rt△ABE≌Rt△DCF的是
.(填序号)?
①AB=DC,∠B=∠C;②AB=DC,AB∥CD;
③AB=DC,BE=CF;④AB=DF,BE=CF.
10.如图,有两个长度相等的滑梯,左边滑梯BC的高度AC与右边滑梯EF水平方向的长度DF相等,则两个滑梯的倾斜角∠ABC和∠DFE有什么关系?
11.如图,AD,AF分别是两个钝角△ABC和△ABE的高,AD=AF,AC=AE.求证:BC=BE.
12.如图,在△ABC和△DEF中,∠B=∠E=90°,BC=EF,CM为△ABC的中线,FN为△DEF的中线,且CM=FN.求证:△ABC≌△DEF.
13.在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
(1)如图1,若点B,C在DE的同侧,且AD=CE.求证:AB⊥AC.
(2)如图2,若点B,C在DE的两侧,且AD=CE,其他条件不变,AB与AC仍垂直吗?请说明理由.
第4课时 利用斜边、直角边判定直角三角形全等(HL)
知识点1 用“HL”判定直角三角形全等
1.如图,OD⊥AB于点D,OP⊥AC于点P,且OD=OP,则△AOD与△AOP全等的理由是(
D
)
A.SSS
B.ASA
C.SAS
D.HL
第1题图
第2题图
2.[教材P42例5改编]如图,在△ABC和△BAD中,已知∠C=∠D=90°,再添加一个条件,就可以用“HL”判定Rt△ABC≌Rt△BAD,你添加的条件是 AC=BD(或AD=BC) .?
3.如图,在△ABC中,M是BC的中点,ME⊥AB,MF⊥AC,垂足分别为E,F,ME=MF.求证:△BEM≌△CFM.
证明:∵M是BC的中点,∴BM=CM.
∵ME⊥AB,MF⊥AC,∴∠BEM=∠CFM=90°.
在Rt△BEM和Rt△CFM中,
∴Rt△BEM≌Rt△CFM(HL).
知识点2 直角三角形全等的应用
4.如图,已知∠B=∠D=90°,BC=CD,∠1=40°,则∠2的度数为(
B
)
A.40°
B.50°
C.60°
D.75°
第4题图
第5题图
5.如图,小明和小芳以相同的速度同时分别从点A,B出发,小明沿AC行走,小芳沿BD行走,并且同时到达点C,D.若CB⊥AB,DA⊥AB,则CB = DA.(填“>”“<”或“=”)?
6.如图,工人师傅制作了一个正方形窗架,把窗架立在墙上之前,在上面钉了两根等长的木条GF与GE,E,F分别是AD,BC的中点.
(1)G一定是AB的中点吗?说明理由.
(2)钉这两根木条的作用是什么?
解:(1)G一定是AB的中点,
理由:在正方形ABCD中,AD=BC,∠A=∠B=90°,
∵E,F分别是AD,BC的中点,∴AE=BF.
在Rt△AEG和Rt△BFG中,
∴△AEG≌△BFG(HL),∴AG=BG,
∴G一定是AB的中点.
(2)结合图形可知,利用三角形的稳定性,使窗架更稳固.
7.如图,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD和CE相交于点O,AO的延长线交BC于点F,则图中全等的直角三角形有(
D
)
A.3对
B.4对
C.5对
D.6对
第7题图
第8题图
8.如图,∠ADC=∠ABC=90°,AD=AB,有下列结论:①DC=BC;②AC⊥BD;③DE=BE;④∠ACD=∠ACB.其中正确结论的个数为(
D
)
A.1
B.2
C.3
D.4
9.[教材P43练习第2题改编]如图所示,已知BE⊥AD,CF⊥AD,垂足分别为E,F,则在下列条件中选择一组,可以判定
Rt△ABE≌Rt△DCF的是 ①②③ .(填序号)?
①AB=DC,∠B=∠C;②AB=DC,AB∥CD;
③AB=DC,BE=CF;④AB=DF,BE=CF.
10.如图,有两个长度相等的滑梯,左边滑梯BC的高度AC与右边滑梯EF水平方向的长度DF相等,则两个滑梯的倾斜角∠ABC和∠DFE有什么关系?
解:∠ABC与∠DFE互余.
理由:在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL),
∴∠ABC=∠DEF.
又∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°,
即两个滑梯的倾斜角∠ABC与∠DFE互余.
11.如图,AD,AF分别是两个钝角△ABC和△ABE的高,AD=AF,AC=AE.求证:BC=BE.
证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL),∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL),
∴BD=BF,∴BD-CD=BF-EF,即BC=BE.
12.如图,在△ABC和△DEF中,∠B=∠E=90°,BC=EF,CM为△ABC的中线,FN为△DEF的中线,且CM=FN.求证:△ABC≌△DEF.
证明:在Rt△BCM和Rt△EFN中,
∴Rt△BCM≌Rt△EFN(HL),∴BM=EN.
∵CM为△ABC的中线,FN为△DEF的中线,∴AB=DE.
在△ABC和△DEF中,
∴△ABC≌△DEF(SAS).
13.在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
(1)如图1,若点B,C在DE的同侧,且AD=CE.求证:AB⊥AC.
(2)如图2,若点B,C在DE的两侧,且AD=CE,其他条件不变,AB与AC仍垂直吗?请说明理由.
解:(1)∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°.
易证Rt△ABD≌Rt△CAE,∴∠DAB=∠ECA.
∵∠ECA+∠EAC=90°,∴∠DAB+∠EAC=90°,
∴∠BAC=180°-(∠DAB+∠EAC)=90°,
∴AB⊥AC.
(2)AB⊥AC.
理由:易证Rt△ABD≌Rt△CAE,∴∠DAB=∠ECA.
∵∠CAE+∠ECA=90°,∴∠CAE+∠DAB=90°,
即∠BAC=90°,∴AB⊥AC.
