1.2.8二次函数的图像和性质——对称性_教案-湘教版必修一
文档属性
| 名称 | 1.2.8二次函数的图像和性质——对称性_教案-湘教版必修一 |

|
|
| 格式 | doc | ||
| 文件大小 | 119.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 00:00:00 | ||
图片预览

文档简介
二次函数的图像和性质——对称性
【教学目标】
一、知识与技能:
1.通过对二次函数性质习题的讲评,使学生熟练掌握二次函数的图像与性质。
2.懂得从图像中获取有关的性质信息。
3.使学生会通过二次函数图像的对称性解决相应问题。
二、过程与方法:通过数形结合理解二次函数的对称性性质。
三、情感态度与价值观:培养数形结合思想,体验函数具体解决现实问题的功能。
【教学重点】
如何在图像中获取有用的信息。
【教学难点】
对称性质的综合应用
【教学过程】
一、引入:华罗庚说过:“数缺形时少直观,形少数时难入微”要真正的研究数学就应该数形结合,研究函数就是用数形结合的思想
二次函数是函数问题中的主要内容,中考试题中年年考查,可以出简单题、中档题甚至于综合性难题,但实际上有相当一部分的题型都跟二次函数的图像与性质有关,本节课通过对习题进行讲评,使同学们熟练掌握二次函数的图像与性质尤其对称性这一性质。
二、讲评:
1.抛物线y=ax?+bx+c(a≠0)的性质:
总结抛物线的性质:
a.b.c的代数式 作用 说明
a 1.a的正负决定抛物线的开口方向;
2.决定抛物线开口大小
开口向上
开口向下
b 决定对称轴的位置,对称轴为直线 a.b同号 对称轴在y轴左侧
b=0 对称轴在y轴
a.b异号 对称轴在y轴右侧
c 确定抛物线与y轴交点的位置,交点坐标(0,c)
交点在y轴的正半轴
交点是原点
交点在y轴的负半轴
决定抛物线与x轴交点个数
抛物线与x轴有2个交点
抛物线与x轴有1个交点
抛物线与x轴有0个交点
决定顶点位置 时,顶点纵坐标是二次函数的最小值。
时,顶点纵坐标是二次函数的最大值。
决定抛物线与x轴交点的横坐标 当时,即,则抛物线与轴的交点坐标为
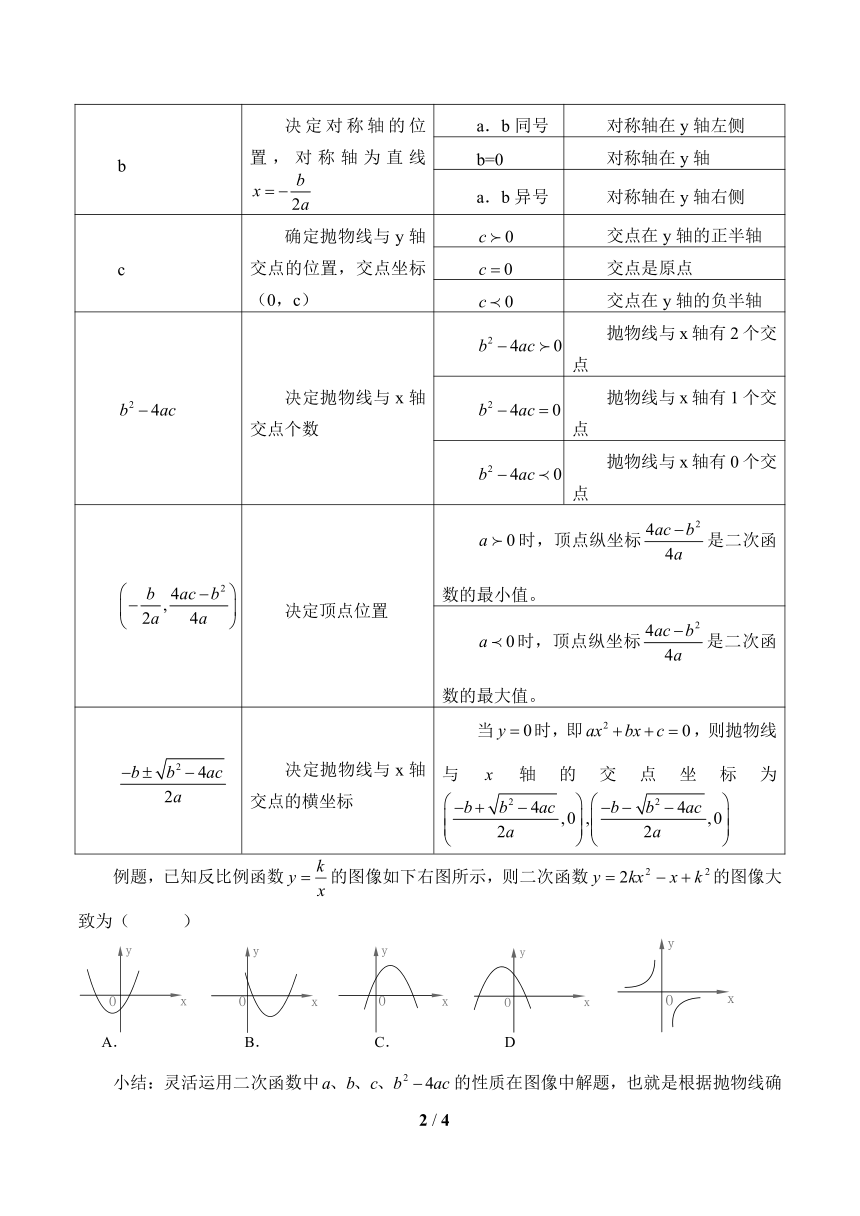
例题,已知反比例函数的图像如下右图所示,则二次函数的图像大致为( )
小结:灵活运用二次函数中的性质在图像中解题,也就是根据抛物线确定二次函数解析式中字母系数的取值范围,很好地体现了数形结合的数学思想,这就需要大家对于二次函数的性质与图像要比较熟悉,并能在图像中从这些性质来思考解决问题的思路。
2.图像对称性
例:二次函数y=ax?+bx+c的图像与x轴相交于(-1, 0)和(5, 0)两点, 则该抛物线的对称轴是
小结:二次函数的对称性:二次函数的图像是一个关于对称轴
对称的轴对称图形,当抛物线上两点的纵坐标相同,即时,。
3.通过例题的解析,得出几条关于二次函数对称性的几个结论:
(1)若抛物线与轴的两个交点是A(x1,0),B(x?,0),则抛物线的对称轴是:
(2)抛物线上两个不同点P1(x1,y1),P2(x?,y?),若有y1=y?,则P1,P2两点是关于抛物线对称轴对称的点,且这时抛物线的对称轴是直线:
三、二次函数对称性综合题
巧用“对称性” 化繁为简
抛物线y=a(x+1)?+2的一部分如图所示,该抛物线在y轴右侧部分与x轴交点的坐标是 ______
已知关于x的方程ax?+bx+c=3的一个根为x1=2,且二次函数y=ax?+bx+c的对称轴直线是x=2,则抛物线的顶点坐标是( )
A.(2,-3 ) B.(2,1) C.(2,3) D.(3,2)
运用二次函数的对称性求方程的根
已知二次函数y=ax?+bx+c(a≠0)的顶点坐标为(-1,-3.2)及部分图像如图,由图像可知关于x的一元二次方程ax?+bx+c=0的两根分别为x1=1.3,x?=_____
巧用“对称性”求距离和差最值如图,抛物线y=0.5x?+bx-2与x轴交于A,B两点,与y轴交于C点,顶点为D,且A(-1,0)。若点 M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值。
【教学反思】
1.抛物线y=ax?+bx+c(a≠0)的性质:
图像的位置
抛物线的增减性。
抛物线的对称性。
最值问题
2.抛物线的对称性的在解题中的使用。
4 / 4
【教学目标】
一、知识与技能:
1.通过对二次函数性质习题的讲评,使学生熟练掌握二次函数的图像与性质。
2.懂得从图像中获取有关的性质信息。
3.使学生会通过二次函数图像的对称性解决相应问题。
二、过程与方法:通过数形结合理解二次函数的对称性性质。
三、情感态度与价值观:培养数形结合思想,体验函数具体解决现实问题的功能。
【教学重点】
如何在图像中获取有用的信息。
【教学难点】
对称性质的综合应用
【教学过程】
一、引入:华罗庚说过:“数缺形时少直观,形少数时难入微”要真正的研究数学就应该数形结合,研究函数就是用数形结合的思想
二次函数是函数问题中的主要内容,中考试题中年年考查,可以出简单题、中档题甚至于综合性难题,但实际上有相当一部分的题型都跟二次函数的图像与性质有关,本节课通过对习题进行讲评,使同学们熟练掌握二次函数的图像与性质尤其对称性这一性质。
二、讲评:
1.抛物线y=ax?+bx+c(a≠0)的性质:
总结抛物线的性质:
a.b.c的代数式 作用 说明
a 1.a的正负决定抛物线的开口方向;
2.决定抛物线开口大小
开口向上
开口向下
b 决定对称轴的位置,对称轴为直线 a.b同号 对称轴在y轴左侧
b=0 对称轴在y轴
a.b异号 对称轴在y轴右侧
c 确定抛物线与y轴交点的位置,交点坐标(0,c)
交点在y轴的正半轴
交点是原点
交点在y轴的负半轴
决定抛物线与x轴交点个数
抛物线与x轴有2个交点
抛物线与x轴有1个交点
抛物线与x轴有0个交点
决定顶点位置 时,顶点纵坐标是二次函数的最小值。
时,顶点纵坐标是二次函数的最大值。
决定抛物线与x轴交点的横坐标 当时,即,则抛物线与轴的交点坐标为
例题,已知反比例函数的图像如下右图所示,则二次函数的图像大致为( )
小结:灵活运用二次函数中的性质在图像中解题,也就是根据抛物线确定二次函数解析式中字母系数的取值范围,很好地体现了数形结合的数学思想,这就需要大家对于二次函数的性质与图像要比较熟悉,并能在图像中从这些性质来思考解决问题的思路。
2.图像对称性
例:二次函数y=ax?+bx+c的图像与x轴相交于(-1, 0)和(5, 0)两点, 则该抛物线的对称轴是
小结:二次函数的对称性:二次函数的图像是一个关于对称轴
对称的轴对称图形,当抛物线上两点的纵坐标相同,即时,。
3.通过例题的解析,得出几条关于二次函数对称性的几个结论:
(1)若抛物线与轴的两个交点是A(x1,0),B(x?,0),则抛物线的对称轴是:
(2)抛物线上两个不同点P1(x1,y1),P2(x?,y?),若有y1=y?,则P1,P2两点是关于抛物线对称轴对称的点,且这时抛物线的对称轴是直线:
三、二次函数对称性综合题
巧用“对称性” 化繁为简
抛物线y=a(x+1)?+2的一部分如图所示,该抛物线在y轴右侧部分与x轴交点的坐标是 ______
已知关于x的方程ax?+bx+c=3的一个根为x1=2,且二次函数y=ax?+bx+c的对称轴直线是x=2,则抛物线的顶点坐标是( )
A.(2,-3 ) B.(2,1) C.(2,3) D.(3,2)
运用二次函数的对称性求方程的根
已知二次函数y=ax?+bx+c(a≠0)的顶点坐标为(-1,-3.2)及部分图像如图,由图像可知关于x的一元二次方程ax?+bx+c=0的两根分别为x1=1.3,x?=_____
巧用“对称性”求距离和差最值如图,抛物线y=0.5x?+bx-2与x轴交于A,B两点,与y轴交于C点,顶点为D,且A(-1,0)。若点 M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值。
【教学反思】
1.抛物线y=ax?+bx+c(a≠0)的性质:
图像的位置
抛物线的增减性。
抛物线的对称性。
最值问题
2.抛物线的对称性的在解题中的使用。
4 / 4
