2.5.2形形色色的函数模型_教案-湘教版必修一
文档属性
| 名称 | 2.5.2形形色色的函数模型_教案-湘教版必修一 |

|
|
| 格式 | doc | ||
| 文件大小 | 198.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 00:00:00 | ||
图片预览

文档简介
指数爆炸和指数衰减
【教学目标】
1.理解指数函数的概念
2.会作指数函数图象的草图(a>1)。
3.学会从函数图象中得到指数函数的性质,感悟数形结合的思想方法。
【教学重点】
结合图象研究函数的性质
【教学难点】
经过概括,领会函数的图象及性质
【教学过程】
一、复习与练习
1.考察幂。(1)当时,是一个怎样的数?用根式形式表示;(2)当时,表示什么含义,能给出它的大致范围吗?(3)任意取定一个实数x,实数是否唯一?
2.比较两个数的大小:
(1)与;(2)与。
二、引入新课
1.指数函数。
函数叫做指数函数,指数函数的定义域是全体实数。
请思考:(1)定义中为什么规定a>0,且a≠1?
(2)a>0时函数y=ax中,值y有可能是0或负数吗,为什么?
2.指数函数y=的图象。
(1)我们先考察a=2时,的图象(能不能事先想象图象的大致情况和走向?用语言大致描述一下)。
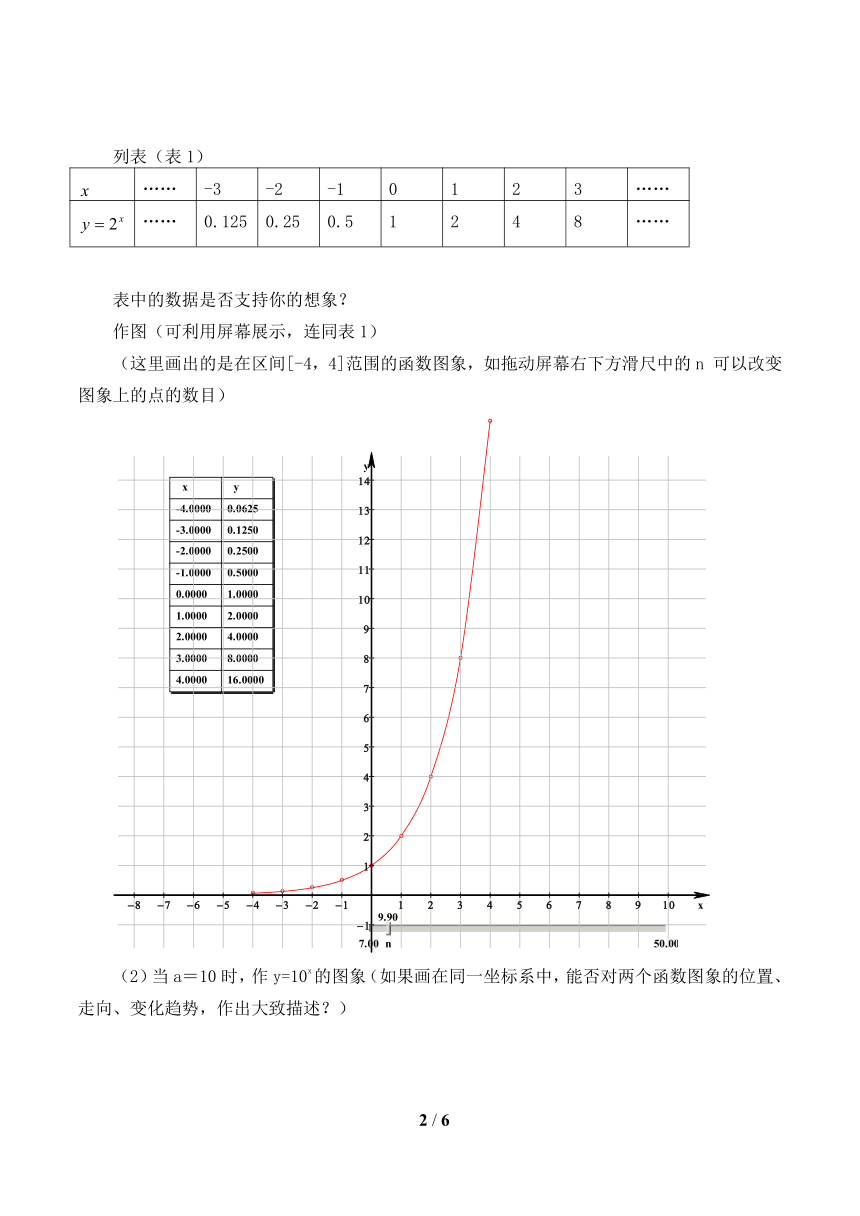
列表(表1)
…… -3 -2 -1 0 1 2 3 ……
…… 0.125 0.25 0.5 1 2 4 8 ……
表中的数据是否支持你的想象?
作图(可利用屏幕展示,连同表1)
(这里画出的是在区间[-4,4]范围的函数图象,如拖动屏幕右下方滑尺中的n 可以改变图象上的点的数目)
(2)当a=10时,作y=10x的图象(如果画在同一坐标系中,能否对两个函数图象的位置、走向、变化趋势,作出大致描述?)
列表(数据续在表1中,构成表2)
…… -3 -2 -1 0 1 2 3 ……
…… 0.125 0.25 0.5 1 2 4 8 ……
…… 0.001 0.01 0.1 1 10 100 1000 ……
作图(可利用屏幕,在同一坐标系中展示连同表2)
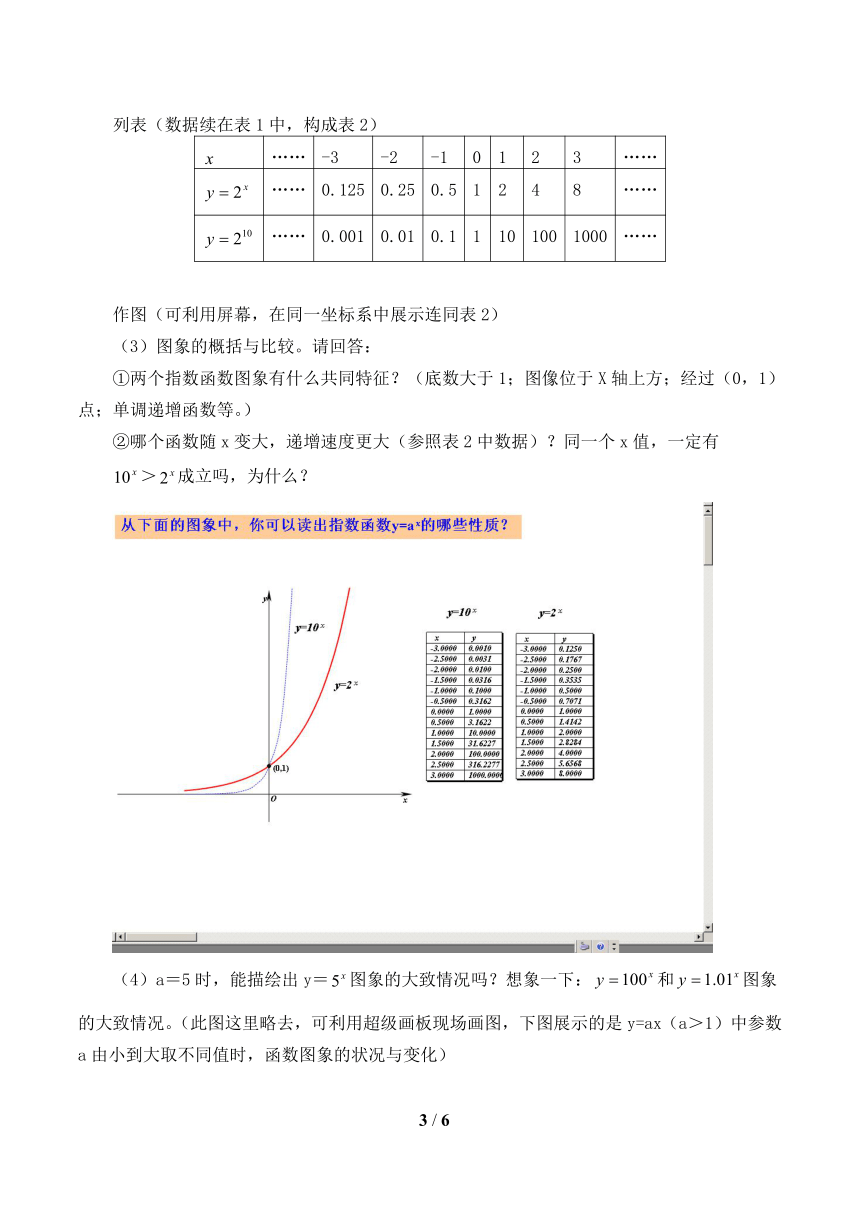
(3)图象的概括与比较。请回答:
①两个指数函数图象有什么共同特征?(底数大于1;图像位于X轴上方;经过(0,1)点;单调递增函数等。)
②哪个函数随x变大,递增速度更大(参照表2中数据)?同一个x值,一定有
>成立吗,为什么?
(4)a=5时,能描绘出y=图象的大致情况吗?想象一下:和图象的大致情况。(此图这里略去,可利用超级画板现场画图,下图展示的是y=ax(a>1)中参数a由小到大取不同值时,函数图象的状况与变化)
3.指数函数y=ax(a>1)的性质
利用图象,我们可以得到哪些基本性质?(先口头交流;再阅读课本84页;最后教师一一列出进一步明确与强调。)
(1)图象总在x轴上方,是实数到正实数之间的一个映射。
即>0恒成立。
(2)图象都过点(0,1)
即=1
(3)a>1时,函数在区间(-∞,+∞)单调递增
即任意实数x1,x2,x1<x2时,总有下式成立:
<
特别地,有
①令x1=0,任意x2>x1=0
>==1
②令x2=0,任意x1 <x2=0
<==1
4.简单应用
注意到,指数函数y=(a>1)是单调(递增)函数,这是一个实数x与正实数y之间的一种一一对应关系。我们以y=为例,观察它的图象(屏幕展示)
当≠时,必有≠(即≠)
反过来,当≠时,必有≠
例1.求x
(1)=16; (2)=; (3)=3; (4)=1
例2.求x的取值范围
(1)>2;(2)<;(3)<1
例3.比较下列各组数间的大小:
(1)2.11.5与2.11.4;(2)与;
(3)x>0时,与; (4)x<0时,与。
例4.利用图象,估计x的取值范围
=6
三、小结
1.“数形结合”是理解和研究函数性质的重要方法。函数的解析式表达了变量之间的相依关系,描述了“动点”运动变化的过程。图象从整体上给出了函数的直观形象,对于图象要以动态的观点来解读和考察。
2.通过取a的值为2.10.5等,来研究一般函数y=ax(a>1)的性质,这是一个归纳、概括的活动。抽取它们共有的本质特征,是从特殊到一般的过程。这是一种重要的数学思想方法。
3.要学会从函数图象中获取函数性质的相关信息。
【作业布置】
在同一坐标系中作出下列函数图象:
(1)y=与y=-1;(2)y=与y=
(补充题可以利用变换法对图象进行平移,也允许采用列表描图的方法。)
4 / 6
【教学目标】
1.理解指数函数的概念
2.会作指数函数图象的草图(a>1)。
3.学会从函数图象中得到指数函数的性质,感悟数形结合的思想方法。
【教学重点】
结合图象研究函数的性质
【教学难点】
经过概括,领会函数的图象及性质
【教学过程】
一、复习与练习
1.考察幂。(1)当时,是一个怎样的数?用根式形式表示;(2)当时,表示什么含义,能给出它的大致范围吗?(3)任意取定一个实数x,实数是否唯一?
2.比较两个数的大小:
(1)与;(2)与。
二、引入新课
1.指数函数。
函数叫做指数函数,指数函数的定义域是全体实数。
请思考:(1)定义中为什么规定a>0,且a≠1?
(2)a>0时函数y=ax中,值y有可能是0或负数吗,为什么?
2.指数函数y=的图象。
(1)我们先考察a=2时,的图象(能不能事先想象图象的大致情况和走向?用语言大致描述一下)。
列表(表1)
…… -3 -2 -1 0 1 2 3 ……
…… 0.125 0.25 0.5 1 2 4 8 ……
表中的数据是否支持你的想象?
作图(可利用屏幕展示,连同表1)
(这里画出的是在区间[-4,4]范围的函数图象,如拖动屏幕右下方滑尺中的n 可以改变图象上的点的数目)
(2)当a=10时,作y=10x的图象(如果画在同一坐标系中,能否对两个函数图象的位置、走向、变化趋势,作出大致描述?)
列表(数据续在表1中,构成表2)
…… -3 -2 -1 0 1 2 3 ……
…… 0.125 0.25 0.5 1 2 4 8 ……
…… 0.001 0.01 0.1 1 10 100 1000 ……
作图(可利用屏幕,在同一坐标系中展示连同表2)
(3)图象的概括与比较。请回答:
①两个指数函数图象有什么共同特征?(底数大于1;图像位于X轴上方;经过(0,1)点;单调递增函数等。)
②哪个函数随x变大,递增速度更大(参照表2中数据)?同一个x值,一定有
>成立吗,为什么?
(4)a=5时,能描绘出y=图象的大致情况吗?想象一下:和图象的大致情况。(此图这里略去,可利用超级画板现场画图,下图展示的是y=ax(a>1)中参数a由小到大取不同值时,函数图象的状况与变化)
3.指数函数y=ax(a>1)的性质
利用图象,我们可以得到哪些基本性质?(先口头交流;再阅读课本84页;最后教师一一列出进一步明确与强调。)
(1)图象总在x轴上方,是实数到正实数之间的一个映射。
即>0恒成立。
(2)图象都过点(0,1)
即=1
(3)a>1时,函数在区间(-∞,+∞)单调递增
即任意实数x1,x2,x1<x2时,总有下式成立:
<
特别地,有
①令x1=0,任意x2>x1=0
>==1
②令x2=0,任意x1 <x2=0
<==1
4.简单应用
注意到,指数函数y=(a>1)是单调(递增)函数,这是一个实数x与正实数y之间的一种一一对应关系。我们以y=为例,观察它的图象(屏幕展示)
当≠时,必有≠(即≠)
反过来,当≠时,必有≠
例1.求x
(1)=16; (2)=; (3)=3; (4)=1
例2.求x的取值范围
(1)>2;(2)<;(3)<1
例3.比较下列各组数间的大小:
(1)2.11.5与2.11.4;(2)与;
(3)x>0时,与; (4)x<0时,与。
例4.利用图象,估计x的取值范围
=6
三、小结
1.“数形结合”是理解和研究函数性质的重要方法。函数的解析式表达了变量之间的相依关系,描述了“动点”运动变化的过程。图象从整体上给出了函数的直观形象,对于图象要以动态的观点来解读和考察。
2.通过取a的值为2.10.5等,来研究一般函数y=ax(a>1)的性质,这是一个归纳、概括的活动。抽取它们共有的本质特征,是从特殊到一般的过程。这是一种重要的数学思想方法。
3.要学会从函数图象中获取函数性质的相关信息。
【作业布置】
在同一坐标系中作出下列函数图象:
(1)y=与y=-1;(2)y=与y=
(补充题可以利用变换法对图象进行平移,也允许采用列表描图的方法。)
4 / 6
