湘教版必修一 函数中的“倚天剑”——数形结合思想 教案设计
文档属性
| 名称 | 湘教版必修一 函数中的“倚天剑”——数形结合思想 教案设计 |  | |
| 格式 | doc | ||
| 文件大小 | 602.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 12:55:40 | ||
图片预览



文档简介
函数中的“倚天剑”——数形结合思想
教 案 设 计
【教学目标】
通过例题1和训练1体会“数”的精准性,规范严密性的优点,体会“形”的生动性与直观性的特点;通过例题2和训练2掌握数形结合思想使用时的三个原则:等价性、双方性、简单性;通过例题3和训练3体会数与形的相互作用,相互转化,提高学生综合解决问题的能力。
2、体会数与形间的联系,激发学习兴趣,训练迁移转化的思维方法与能力。
【教学重点】
以形助数、以数辅形
【教学难点】
画函数图像的精准度;等价转化的能力
【教学方法】
讲练结合法
【教学手段】
多媒体应用
【教学过程】
一、教学引入
前不久热播了一部电视剧《倚天屠龙记2019版》,剧中“倚天剑”是江湖中的一把利器,数形结合思想也是解决函数问题的一个得力工具。高三李华同学近几次的数学月考成绩:67,85,107,89,123,119.一堆数据摆在这里很准确,但很枯燥。如果我把这些数据通过excel生成图形。
怎么样?什么感觉?直观性很强,但有颜值没有内容,如果图形中有数的刻画那就“有颜有料”了。
伟大数学家华罗庚先生曾这样描述“数”与“形”之间的密切联系:
数缺形时少直观,
形少数时难入微,
数形结合百般好,
隔离分家万事休。
二、教学内容
(一)、近三年全国二卷对于数形结合的考查
这么好的思想方法当然也是高考的“宠儿”“热点”。下面在我们看一下近三年全国二卷对于数形结合思想的考查。
大题部分:
2016年 2017年 2018年
19题 立体几何 19题 立体几何 19题 抛物线
20题 椭圆 20题 圆锥曲线 20题 立体几何
21题 函数与导数 21题 函数与导数 21题 函数与导数
22题 直线与圆 22题 极坐标与参数 22题 直线与椭圆
小题部分:
2016年 2017年 2018年
4题 直线与圆 4题 三视图 3题 函数图像
5题 排列组合 5题 线性规划 6题 解三角形
6题 三视图 9题 双曲线求离心率 7题 异面直线的角
10题 几何概型 10题 异面直线的角 10题 三角函数的单调性
11题 双曲线求离心率 11题 函数的极值点 11题 函数的性质
12题 函数的性质 12题 向量数量积 12题 椭圆离心率
13题 解三角形 14题 三角函数求最值 14题 线性规划
14题 线面位置关系 16题 抛物线 16题 圆锥侧面积
从表格可以看出,数形结合思想功能强大,应用广泛;而对于函数性质的考查出现在试卷的11题和12题的位置。也就是试卷中的瓶颈题,怎样才能更好的解决这类问题。今天我们一起来探究函数中的数形结合思想。
(二)、应用举例
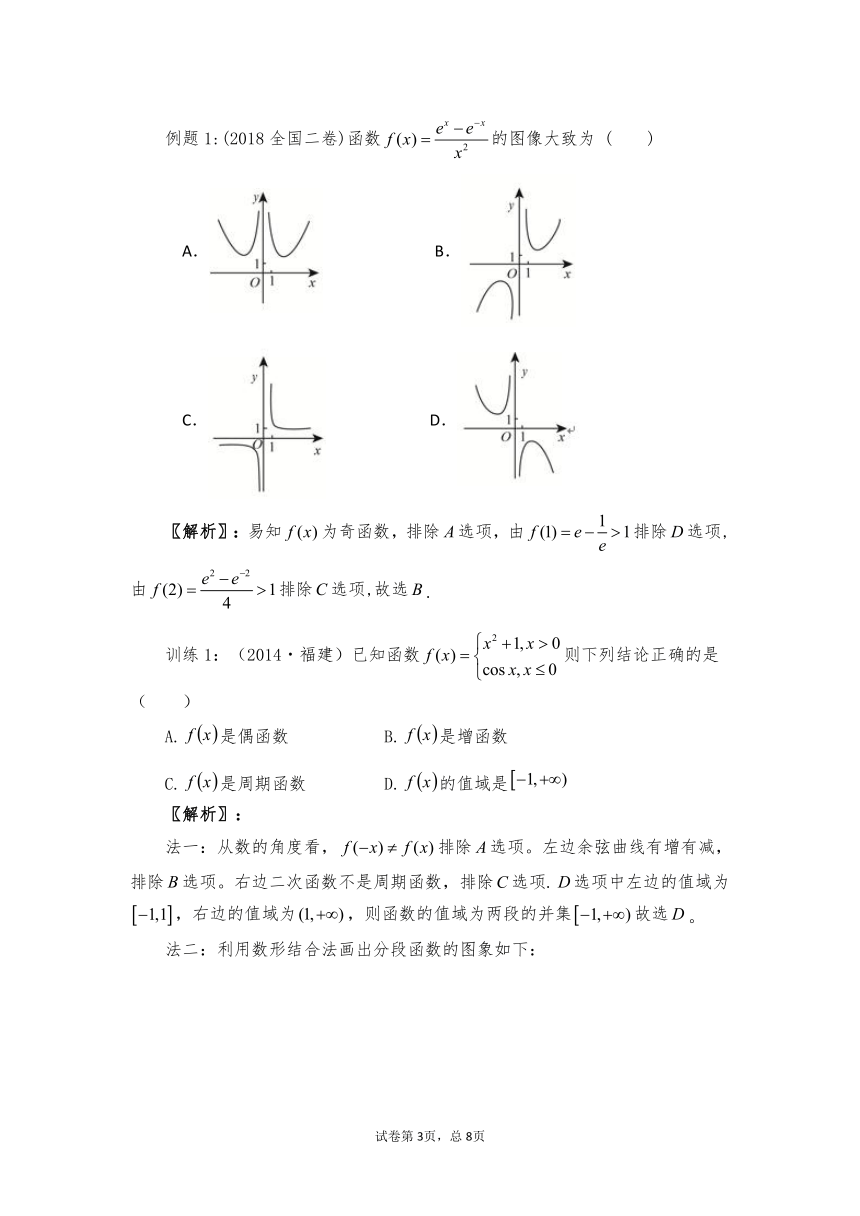
例题1:(2018全国二卷)函数的图像大致为 ( )
A. B.
C. D.
〖解析〗:易知为奇函数,排除选项,由排除选项,由排除选项,故选.
训练1:(2014˙福建)已知函数则下列结论正确的是( )
A.是偶函数 B.是增函数
C.是周期函数 D.的值域是
〖解析〗:
法一:从数的角度看,排除选项。左边余弦曲线有增有减,排除选项。右边二次函数不是周期函数,排除选项.选项中左边的值域为,右边的值域为,则函数的值域为两段的并集故选。
法二:利用数形结合法画出分段函数的图象如下:
由图可知,选.
设计意图:总结数形结合思想的两个内容:(1)以数辅形(2)以形助数。
例题2.方程有唯一实数解,则实数的取值范围是
〖解析〗:
法一(数形结合法):画出函数与函数的图象,观察它们的交点情况:
法二(三角代换法):令,
则,,结合正弦曲线的图象可知,方程只有一解则或
法三(转化法):由原方程变形得:画出函数与函数的图象,观察它们的交点情况:
训练2:已知定义在R上的函数,若,且,则 .
〖解析〗:画出该分段函数的图象:
由图可知,关于对称,所以,而在图中是看不出来的,
所以我们只能进行数的运算:
故。
例3:若函数有三个不同的零点,则的取值范围是( )
〖解析〗:
法一:由得:分别画出和两个函数的图象,显然,且在图象的左边有1个交点,当两曲线在右边有2个交点时,符合题意,两个交点的临界条件是相切,设切点横坐标为,则解得所以,因为指数增长比次数增长更快,所以由图可知.
法二:(分参)由知所以,分别画出和两个函数的图象,由图象观察交点情况即可。对于函数求导得,所以单调性情况应该是:在和上单增;在上单减。
由图可知.
训练3:(2018˙天津卷)已知,函数。若关
于的方程恰有2个互异的实数解,则的取值范围是
〖解析〗:
法一(双函数找交点):当时,由,得;当时,由得令,作出射线和,函数的图象如图所示:
函数的最大值,由图可知,所以。
法二(分参):当时,由,得显然不是方程的实数解,则,当时,由得显然不是方程的实数解则,令,
其中,
作出直线和函数的图象如图所示:
法三(代数判别式法):
①当时,即,且
当时,方程有2个负实数解;
当时,方程有1个负实数解;
当时,方程有0个负实数解;
②当时,即,且
当时,方程有2个正实数解;
当时,方程有1个正实数解;
当时,方程有0个正实数解;
综上所得,实数的取值范围是。
三、课堂小结
1、数形结合思想的两个内容:以形助数、以数辅形;三大原则:等价性,双方性,简单性。
2、新高考的数学核心素养中的数学运算与直观想象就是数形结合思想的重要体现。
3、本堂课我们用到了两个重要的数学思想与方法:数形结合的思想与化归与转化思想。其中数形结合的思想被我喻为“倚天剑”;那化归与转化思想就是“屠龙刀”,掌握好这些数学思想与方法,就能更好的解决数学问题。
希望同学们左手“倚天剑”,右手“屠龙刀”,笑傲高考。祝大家高考成功!谢谢大家。
四、板书设计
数形结合思想
两大内容:1、以数辅形
2、以形助数
三大原则:1、等价性
2、双方性
3、简单性 例题
五、教学反思
试卷第1 11页,总3 33页
教 案 设 计
【教学目标】
通过例题1和训练1体会“数”的精准性,规范严密性的优点,体会“形”的生动性与直观性的特点;通过例题2和训练2掌握数形结合思想使用时的三个原则:等价性、双方性、简单性;通过例题3和训练3体会数与形的相互作用,相互转化,提高学生综合解决问题的能力。
2、体会数与形间的联系,激发学习兴趣,训练迁移转化的思维方法与能力。
【教学重点】
以形助数、以数辅形
【教学难点】
画函数图像的精准度;等价转化的能力
【教学方法】
讲练结合法
【教学手段】
多媒体应用
【教学过程】
一、教学引入
前不久热播了一部电视剧《倚天屠龙记2019版》,剧中“倚天剑”是江湖中的一把利器,数形结合思想也是解决函数问题的一个得力工具。高三李华同学近几次的数学月考成绩:67,85,107,89,123,119.一堆数据摆在这里很准确,但很枯燥。如果我把这些数据通过excel生成图形。
怎么样?什么感觉?直观性很强,但有颜值没有内容,如果图形中有数的刻画那就“有颜有料”了。
伟大数学家华罗庚先生曾这样描述“数”与“形”之间的密切联系:
数缺形时少直观,
形少数时难入微,
数形结合百般好,
隔离分家万事休。
二、教学内容
(一)、近三年全国二卷对于数形结合的考查
这么好的思想方法当然也是高考的“宠儿”“热点”。下面在我们看一下近三年全国二卷对于数形结合思想的考查。
大题部分:
2016年 2017年 2018年
19题 立体几何 19题 立体几何 19题 抛物线
20题 椭圆 20题 圆锥曲线 20题 立体几何
21题 函数与导数 21题 函数与导数 21题 函数与导数
22题 直线与圆 22题 极坐标与参数 22题 直线与椭圆
小题部分:
2016年 2017年 2018年
4题 直线与圆 4题 三视图 3题 函数图像
5题 排列组合 5题 线性规划 6题 解三角形
6题 三视图 9题 双曲线求离心率 7题 异面直线的角
10题 几何概型 10题 异面直线的角 10题 三角函数的单调性
11题 双曲线求离心率 11题 函数的极值点 11题 函数的性质
12题 函数的性质 12题 向量数量积 12题 椭圆离心率
13题 解三角形 14题 三角函数求最值 14题 线性规划
14题 线面位置关系 16题 抛物线 16题 圆锥侧面积
从表格可以看出,数形结合思想功能强大,应用广泛;而对于函数性质的考查出现在试卷的11题和12题的位置。也就是试卷中的瓶颈题,怎样才能更好的解决这类问题。今天我们一起来探究函数中的数形结合思想。
(二)、应用举例
例题1:(2018全国二卷)函数的图像大致为 ( )
A. B.
C. D.
〖解析〗:易知为奇函数,排除选项,由排除选项,由排除选项,故选.
训练1:(2014˙福建)已知函数则下列结论正确的是( )
A.是偶函数 B.是增函数
C.是周期函数 D.的值域是
〖解析〗:
法一:从数的角度看,排除选项。左边余弦曲线有增有减,排除选项。右边二次函数不是周期函数,排除选项.选项中左边的值域为,右边的值域为,则函数的值域为两段的并集故选。
法二:利用数形结合法画出分段函数的图象如下:
由图可知,选.
设计意图:总结数形结合思想的两个内容:(1)以数辅形(2)以形助数。
例题2.方程有唯一实数解,则实数的取值范围是
〖解析〗:
法一(数形结合法):画出函数与函数的图象,观察它们的交点情况:
法二(三角代换法):令,
则,,结合正弦曲线的图象可知,方程只有一解则或
法三(转化法):由原方程变形得:画出函数与函数的图象,观察它们的交点情况:
训练2:已知定义在R上的函数,若,且,则 .
〖解析〗:画出该分段函数的图象:
由图可知,关于对称,所以,而在图中是看不出来的,
所以我们只能进行数的运算:
故。
例3:若函数有三个不同的零点,则的取值范围是( )
〖解析〗:
法一:由得:分别画出和两个函数的图象,显然,且在图象的左边有1个交点,当两曲线在右边有2个交点时,符合题意,两个交点的临界条件是相切,设切点横坐标为,则解得所以,因为指数增长比次数增长更快,所以由图可知.
法二:(分参)由知所以,分别画出和两个函数的图象,由图象观察交点情况即可。对于函数求导得,所以单调性情况应该是:在和上单增;在上单减。
由图可知.
训练3:(2018˙天津卷)已知,函数。若关
于的方程恰有2个互异的实数解,则的取值范围是
〖解析〗:
法一(双函数找交点):当时,由,得;当时,由得令,作出射线和,函数的图象如图所示:
函数的最大值,由图可知,所以。
法二(分参):当时,由,得显然不是方程的实数解,则,当时,由得显然不是方程的实数解则,令,
其中,
作出直线和函数的图象如图所示:
法三(代数判别式法):
①当时,即,且
当时,方程有2个负实数解;
当时,方程有1个负实数解;
当时,方程有0个负实数解;
②当时,即,且
当时,方程有2个正实数解;
当时,方程有1个正实数解;
当时,方程有0个正实数解;
综上所得,实数的取值范围是。
三、课堂小结
1、数形结合思想的两个内容:以形助数、以数辅形;三大原则:等价性,双方性,简单性。
2、新高考的数学核心素养中的数学运算与直观想象就是数形结合思想的重要体现。
3、本堂课我们用到了两个重要的数学思想与方法:数形结合的思想与化归与转化思想。其中数形结合的思想被我喻为“倚天剑”;那化归与转化思想就是“屠龙刀”,掌握好这些数学思想与方法,就能更好的解决数学问题。
希望同学们左手“倚天剑”,右手“屠龙刀”,笑傲高考。祝大家高考成功!谢谢大家。
四、板书设计
数形结合思想
两大内容:1、以数辅形
2、以形助数
三大原则:1、等价性
2、双方性
3、简单性 例题
五、教学反思
试卷第1 11页,总3 33页
