2020-2021学年人教版数学八年级上册11.3.2 多边形的内角和 课件(21张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册11.3.2 多边形的内角和 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 180.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-10-14 23:09:11 | ||
图片预览





文档简介
11.3.2 多边形的内角和
第十一章 三角形
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
前 言
学习目标
1.理解多边形、正多边形以及多边形的内角、外角、对交线等概念。
2.会用不同的方法探索多边形的内角和,并能利用多边形内角和公式解决问题。
重点难点
重点:探索多边形的内角和。
难点:探索多边形内角和时,如何把多边形转化为三角形。
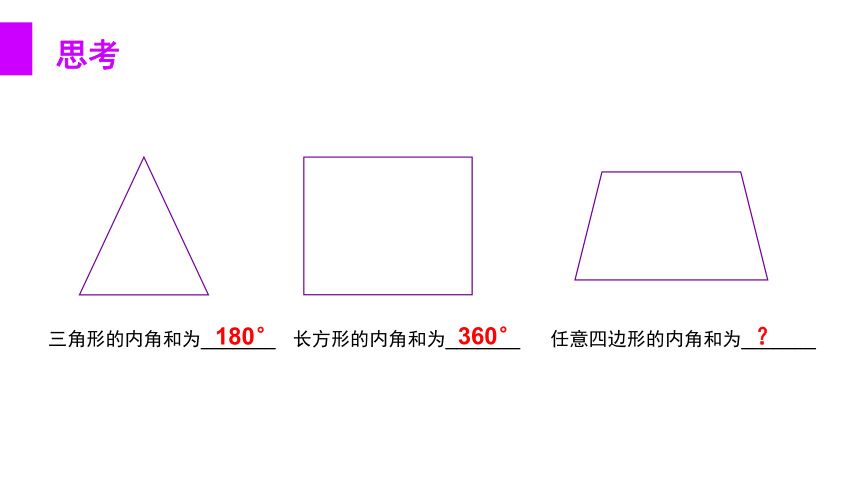
三角形的内角和为_______
长方形的内角和为_______
任意四边形的内角和为_______
180°
360°
?
思考
A
B
C
D
1
2
3
4
连接四边形的任意对角线,将其分为两个三角形,而三角形的内角和为180°,那么任意四边形的内角和是360°吗?
证明:在四边形ABCD中,连接对角线BC,则四边形ABCD被分为△ABC和△BCD两个三角形。
由此可得,
∠A+∠ABD+∠D+∠ACD
=∠A+∠4+∠3+∠D+∠2+∠1
=(∠A+∠3+∠1)+(∠D+∠2+∠4)
而∠A+∠3+∠1=180°
∠D+∠2+∠4=180°
所以∠A+∠ABD+∠D+∠ACD=180°+180°=360°
通过三角形内角和定理
任意四边形内角和是360°
证明
思考
A
B
C
D
E
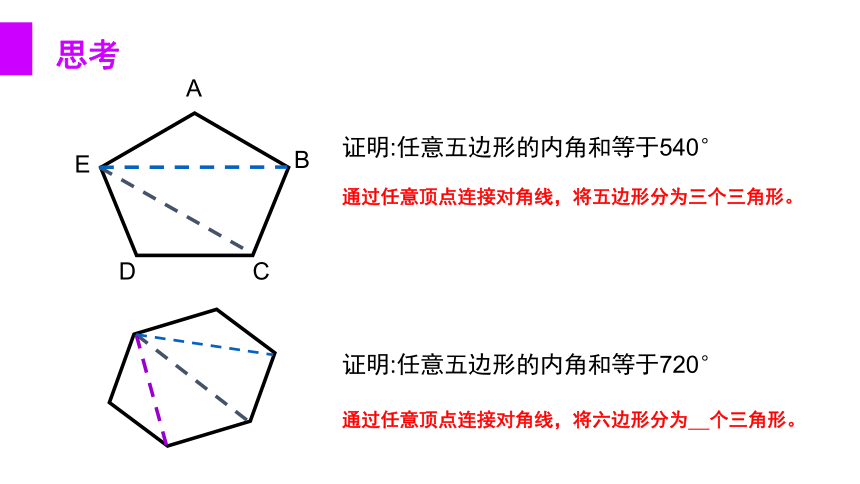
证明:任意五边形的内角和等于540°
通过任意顶点连接对角线,将五边形分为三个三角形。
证明:任意五边形的内角和等于720°
通过任意顶点连接对角线,将六边形分为 个三角形。
思考
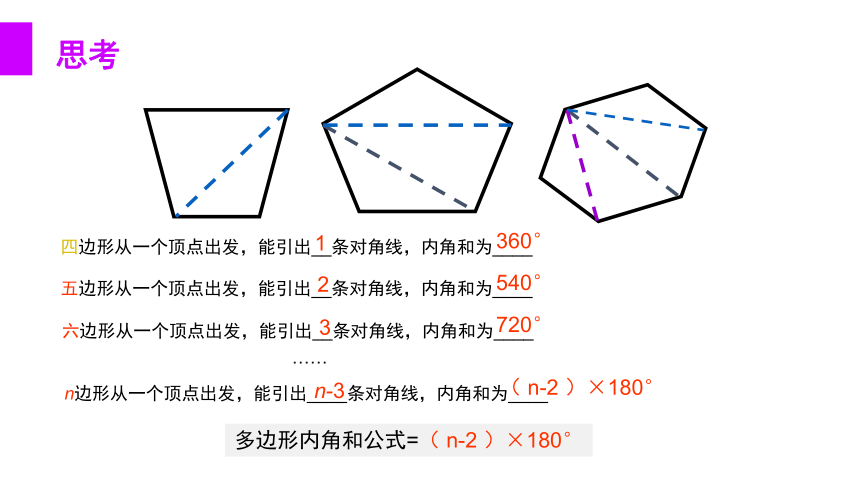
四边形从一个顶点出发,能引出__条对角线,内角和为____
五边形从一个顶点出发,能引出__条对角线,内角和为____
六边形从一个顶点出发,能引出__条对角线,内角和为____
n边形从一个顶点出发,能引出____条对角线,内角和为____
……
1
2
3
n-3
360°
540°
720°
( n-2 )×180°
多边形内角和公式=( n-2 )×180°
思考
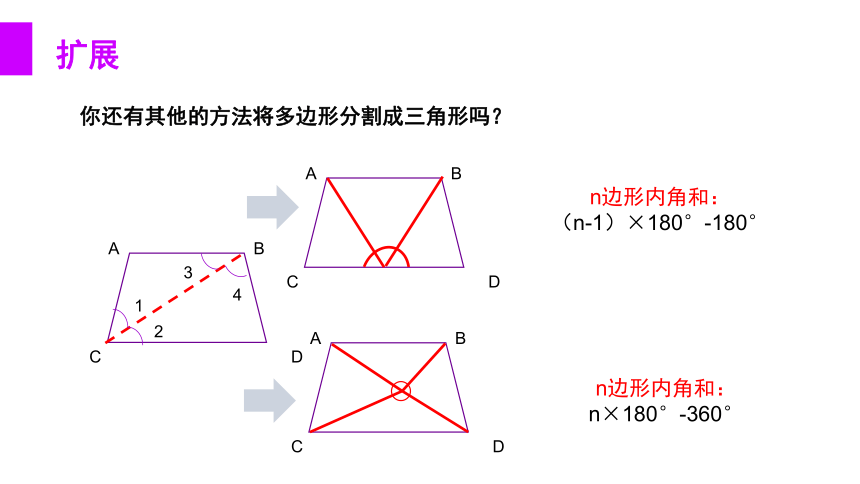
你还有其他的方法将多边形分割成三角形吗?
A
B
C
D
1
2
3
4
A
B
C
D
A
B
C
D
n边形内角和:
(n-1)×180°-180°
n边形内角和:
n×180°-360°
扩展
例1:求八边形的内角和的度数。
解:(n-2)×180°=(8-2)×180° =1080°
答:八边形的内角和为1080°。
课堂测试
例2:填空
(1)十二边形的内角和等于 。
(2)已知一个多边形的内角和等于2340°,它的边数是 。
(3)小明在计算多边形的内角和时求得的度数是1000°,他的答案正确吗?为什么?
1800°
15
(n-1)×180°=1000°
n=???????????? 不能化简为整数,所以不正确
?
课堂测试
(4)已知四边形4个内角的度数比是1︰2︰3︰4,
那么这个四边形中最大角的度是 。
(5)一个五边形的三个内角是直角,另两个内角
都是n°,则n= 。
(6)六角螺母的面是六边形,它的内角都相等,则
这个六边形的每个内角是 。
(7)在四边形ABCD中,∠A与∠C互补,那么∠B
与∠D有什么关系呢?为什么?
144°
135
120°
互补
课堂测试
例3.过多边形一个顶点的所有对角线将这个多边形分成3个三角形,求:
1)这个多边形的边数.
2)这个多边形内角和的度数.
解:根据题意,
对角线将这个多边形分成3个三角形。
所以该多边形是5边形
则(5-2)×180°=540°
课堂测试
1
2
3
4
5
6
在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形外角和。
问题1:任何一个外角同与它相邻的内角有什么关系?
互补
多边形外角和的理解
1
2
3
4
5
6
在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形外角和。
问题2:六边形的6个外角加上与它们相邻的内角,所得总和是多少?
单个外角和它相邻的内角和为180°,所以六边形6个外角与它们相邻内角和为6×180°=1080°
多边形外角和的理解
1
2
3
4
5
6
在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形外角和。
问题3:上述总和与六边形的内角和、外角和有什么关系?
6×180°-(n-2)×180°=360°
多边形外角和的理解
n边形的外角和是多少度呢?
因为多边形的外角与它相邻的内角是邻补角,
所以n边形的外角和加内角和等于n·180°,而内角和为
(n-2)·180°,
外角和为:n·180°-(n-2)·180°= 360°.
结论:多边形的外角和都等于360°.
思考
将左侧的五边形不断缩小后,形成右边图形。由各线段组成夹角和为一个周角,所以多边形内角和为360°
思考
动态演示
例4:一个多边形的内角和等于它的外角和的4倍,它是几边形?
解:设它是n边形,
则(n-2).180=4×360
解得:n=10
答:这个多边形是十边形
课堂测试
例5.如果一个多边形的每一个外角等于30°,则这个多边形的边数是多少?
解:由题意得,多边形的内角为150°,
n边形的内角和为150°×n
则(n-2)×180°=150°×n
即n=12
课堂测试
例6.有一六边形,截去一个三角形,内角和会发生怎样变化?请画图说明。
内角和减少180O
内角和不变
内角和增加180O
变为五边形
边数不变
变为七边形
提高
感谢各位的仔细聆听
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
第十一章 三角形
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
前 言
学习目标
1.理解多边形、正多边形以及多边形的内角、外角、对交线等概念。
2.会用不同的方法探索多边形的内角和,并能利用多边形内角和公式解决问题。
重点难点
重点:探索多边形的内角和。
难点:探索多边形内角和时,如何把多边形转化为三角形。
三角形的内角和为_______
长方形的内角和为_______
任意四边形的内角和为_______
180°
360°
?
思考
A
B
C
D
1
2
3
4
连接四边形的任意对角线,将其分为两个三角形,而三角形的内角和为180°,那么任意四边形的内角和是360°吗?
证明:在四边形ABCD中,连接对角线BC,则四边形ABCD被分为△ABC和△BCD两个三角形。
由此可得,
∠A+∠ABD+∠D+∠ACD
=∠A+∠4+∠3+∠D+∠2+∠1
=(∠A+∠3+∠1)+(∠D+∠2+∠4)
而∠A+∠3+∠1=180°
∠D+∠2+∠4=180°
所以∠A+∠ABD+∠D+∠ACD=180°+180°=360°
通过三角形内角和定理
任意四边形内角和是360°
证明
思考
A
B
C
D
E
证明:任意五边形的内角和等于540°
通过任意顶点连接对角线,将五边形分为三个三角形。
证明:任意五边形的内角和等于720°
通过任意顶点连接对角线,将六边形分为 个三角形。
思考
四边形从一个顶点出发,能引出__条对角线,内角和为____
五边形从一个顶点出发,能引出__条对角线,内角和为____
六边形从一个顶点出发,能引出__条对角线,内角和为____
n边形从一个顶点出发,能引出____条对角线,内角和为____
……
1
2
3
n-3
360°
540°
720°
( n-2 )×180°
多边形内角和公式=( n-2 )×180°
思考
你还有其他的方法将多边形分割成三角形吗?
A
B
C
D
1
2
3
4
A
B
C
D
A
B
C
D
n边形内角和:
(n-1)×180°-180°
n边形内角和:
n×180°-360°
扩展
例1:求八边形的内角和的度数。
解:(n-2)×180°=(8-2)×180° =1080°
答:八边形的内角和为1080°。
课堂测试
例2:填空
(1)十二边形的内角和等于 。
(2)已知一个多边形的内角和等于2340°,它的边数是 。
(3)小明在计算多边形的内角和时求得的度数是1000°,他的答案正确吗?为什么?
1800°
15
(n-1)×180°=1000°
n=???????????? 不能化简为整数,所以不正确
?
课堂测试
(4)已知四边形4个内角的度数比是1︰2︰3︰4,
那么这个四边形中最大角的度是 。
(5)一个五边形的三个内角是直角,另两个内角
都是n°,则n= 。
(6)六角螺母的面是六边形,它的内角都相等,则
这个六边形的每个内角是 。
(7)在四边形ABCD中,∠A与∠C互补,那么∠B
与∠D有什么关系呢?为什么?
144°
135
120°
互补
课堂测试
例3.过多边形一个顶点的所有对角线将这个多边形分成3个三角形,求:
1)这个多边形的边数.
2)这个多边形内角和的度数.
解:根据题意,
对角线将这个多边形分成3个三角形。
所以该多边形是5边形
则(5-2)×180°=540°
课堂测试
1
2
3
4
5
6
在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形外角和。
问题1:任何一个外角同与它相邻的内角有什么关系?
互补
多边形外角和的理解
1
2
3
4
5
6
在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形外角和。
问题2:六边形的6个外角加上与它们相邻的内角,所得总和是多少?
单个外角和它相邻的内角和为180°,所以六边形6个外角与它们相邻内角和为6×180°=1080°
多边形外角和的理解
1
2
3
4
5
6
在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形外角和。
问题3:上述总和与六边形的内角和、外角和有什么关系?
6×180°-(n-2)×180°=360°
多边形外角和的理解
n边形的外角和是多少度呢?
因为多边形的外角与它相邻的内角是邻补角,
所以n边形的外角和加内角和等于n·180°,而内角和为
(n-2)·180°,
外角和为:n·180°-(n-2)·180°= 360°.
结论:多边形的外角和都等于360°.
思考
将左侧的五边形不断缩小后,形成右边图形。由各线段组成夹角和为一个周角,所以多边形内角和为360°
思考
动态演示
例4:一个多边形的内角和等于它的外角和的4倍,它是几边形?
解:设它是n边形,
则(n-2).180=4×360
解得:n=10
答:这个多边形是十边形
课堂测试
例5.如果一个多边形的每一个外角等于30°,则这个多边形的边数是多少?
解:由题意得,多边形的内角为150°,
n边形的内角和为150°×n
则(n-2)×180°=150°×n
即n=12
课堂测试
例6.有一六边形,截去一个三角形,内角和会发生怎样变化?请画图说明。
内角和减少180O
内角和不变
内角和增加180O
变为五边形
边数不变
变为七边形
提高
感谢各位的仔细聆听
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
