2020-2021学年人教版数学八年级上册12.2.2 三角形全等的判定 (SAS)课件(17张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册12.2.2 三角形全等的判定 (SAS)课件(17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 261.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 17:46:40 | ||
图片预览



文档简介
12.2.2 三角形全等的判定 (SAS)
第十二章 全等三角形
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
前 言
学习目标
1.掌握“ 边角边”条件的内容,并能初步应用“ 边角边”条件判定两个三角形全等。
2.使学生经历探索三角形全等条件的过程,体会如何探索研究问题,并初步体会分类思想,提高学生分析问题和解决问题的能力。
3.通过画图、比较、验证,培养学生注重观察、善于思考、不断总结的良好思维习惯。
重点难点
重点:掌握“边角边”判定两个三角形全等的方法。
难点:掌握“边角边”判定两个三角形全等的方法。
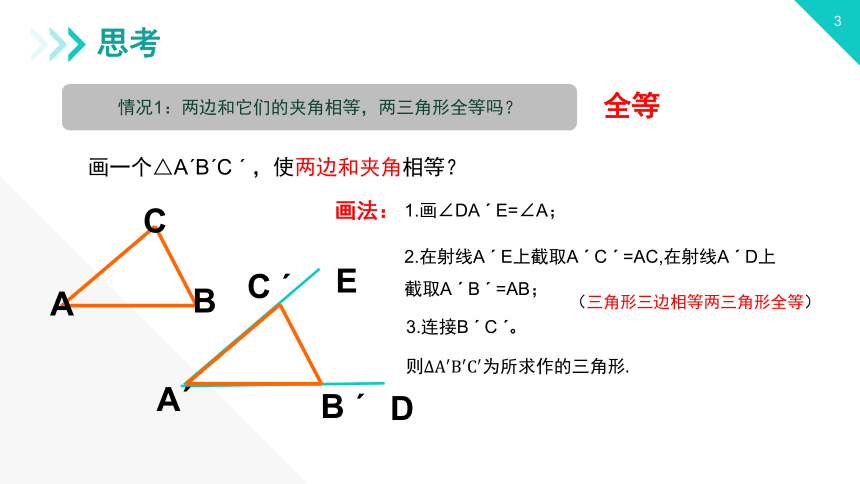
情况1:两边和它们的夹角相等,两三角形全等吗?
画一个△AˊBˊC ˊ ,使两边和夹角相等?
A
B
C
画法:
则ΔA′B′C′为所求作的三角形.
?
Aˊ
B ˊ
C ˊ
D
E
1.画∠DA ˊ E=∠A;
2.在射线A ˊ E上截取A ˊ C ˊ =AC,在射线A ˊ D上截取A ˊ B ˊ =AB;
3.连接B ˊ C ˊ。
(三角形三边相等两三角形全等)
全等
思考
由以上尺规作图的方法可以得到以下基本事实:
两边和它们的夹角分别相等的两个三角形全等。
(即 “ 边角边”或“ SAS”)
小结
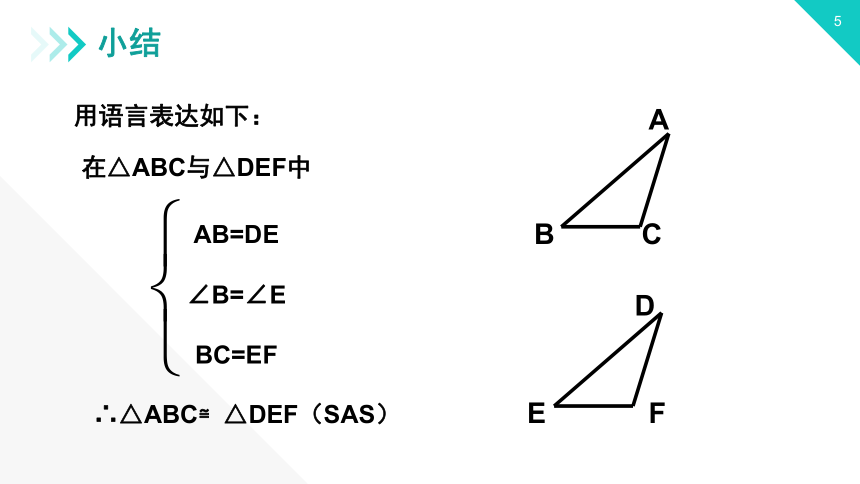
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
用语言表达如下:
小结
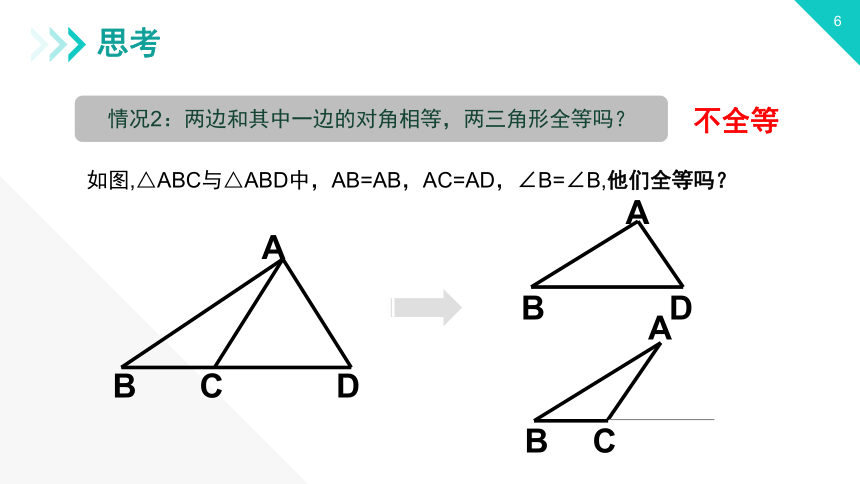
情况2:两边和其中一边的对角相等,两三角形全等吗?
如图,△ABC与△ABD中,AB=AB,AC=AD,∠B=∠B,他们全等吗?
B
A
C
D
B
A
D
B
A
C
不全等
思考
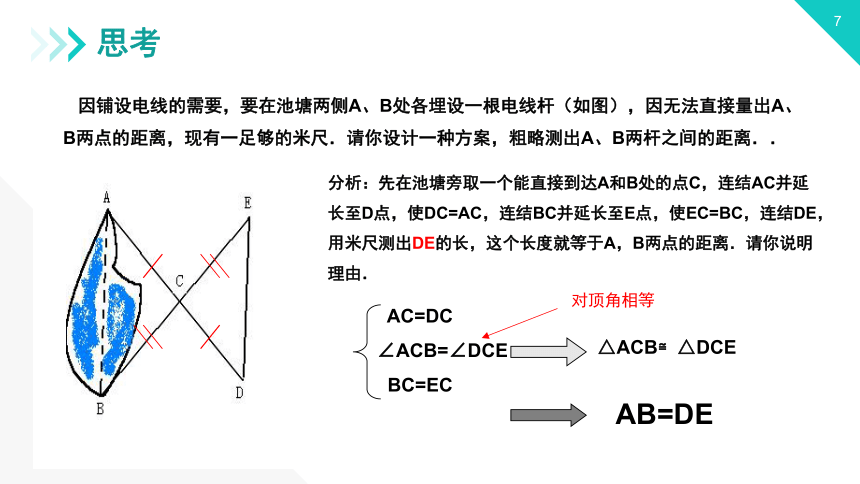
因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺.请你设计一种方案,粗略测出A、B两杆之间的距离..
分析:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使DC=AC,连结BC并延长至E点,使EC=BC,连结DE,用米尺测出DE的长,这个长度就等于A,B两点的距离.请你说明理由.
AC=DC?
∠ACB=∠DCE
BC=EC
△ACB≌△DCE
AB=DE
对顶角相等
思考
A
B
D
O
1.在下列推理中填写需要补充的条件,使结论成立:
(1)如图,在△AOB和△DOC中
AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )
∠ AOB
∠ DOC
对顶角相等
C
SAS
课堂测试
(2)如图,在△AEC和△ADB中,已知AE=AD,AC=AB,请说明△AEC ≌ △ADB的理由。
A
E
B
D
C
____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )
AE
AD
AC
AB
解:在△AEC和△ADB中
SAS
课堂测试
(SAS)
A
B
C
D
2.如图,在四边形ABCD中AB=CD,∠ABD= ∠BDC,则AD=BC.请说明理由。
解:在△ABD和△CDB中
AB=CD (已知)
∠ABD= ∠BDC (已知)
(公共边)
∴ △ABD ≌ △CDB
∴ AD= BC( )
BD=DB
全等三角形的对应边相等
课堂测试
A
B
C
D
3.已知:如图AB=CB ,∠ABD=∠CBD ,△ABD和△CBD全等吗?
解:在△ABD和△CBD中
AB=CB (已知)
∠ABD= ∠CBD (已知)
(公共边)
∴ △ABD ≌ △CBD
BD=BD
(SAS)
课堂测试
4.如图,AC=BD,∠CAB=∠DBA,你能判断BC=AD吗?说明理由.
A
B
C
D
解:在△ACB和△BDA中
AC=BD (已知)
∠CAB= ∠DBA (已知)
(公共边)
∴ △ACB≌ △BDA
AB=BA
∴ BC=AD
(SAS)
课堂测试
A
B
C
D
F
E
1.如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,还需增加一个什么条件?
1.BE = CF (SSS)
2.∠A = ∠D (SAS)
…(答案不唯一)
探索提高
F
C
B
E
D
A
2.如图:己知AD∥BC,AE=CF,AD=BC,E、F都在直线AC上,试说明DE∥BF。
解:在△AED和△CFB中
AE=CF (已知)
∠A=∠C (两直线平行内错角相等)
(已知)
∴ △ AED ≌ △ CFB
AD=BC
∴ ∠D=∠B
∴ ∠D+ ∠A = ∠B+ ∠C 即∠DEF=∠EFB
∴DE∥BF(内错角相等两直线平行)
探索提高
2.如图,AC=BD,∠1= ∠2
求证:BC=AD
变式1: 如图,AC=BD,BC=AD
求证:∠1= ∠2
A
B
C
D
1
2
A
B
C
D
1
2
变式2: 如图,AC=BD,BC=AD
求证:∠C=∠D
A
B
C
D
探索提高
A
B
C
D
变式3: 如图,AC=BD,BC=AD
求证:∠A=∠B
探索提高
感谢各位的仔细聆听
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
第十二章 全等三角形
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
前 言
学习目标
1.掌握“ 边角边”条件的内容,并能初步应用“ 边角边”条件判定两个三角形全等。
2.使学生经历探索三角形全等条件的过程,体会如何探索研究问题,并初步体会分类思想,提高学生分析问题和解决问题的能力。
3.通过画图、比较、验证,培养学生注重观察、善于思考、不断总结的良好思维习惯。
重点难点
重点:掌握“边角边”判定两个三角形全等的方法。
难点:掌握“边角边”判定两个三角形全等的方法。
情况1:两边和它们的夹角相等,两三角形全等吗?
画一个△AˊBˊC ˊ ,使两边和夹角相等?
A
B
C
画法:
则ΔA′B′C′为所求作的三角形.
?
Aˊ
B ˊ
C ˊ
D
E
1.画∠DA ˊ E=∠A;
2.在射线A ˊ E上截取A ˊ C ˊ =AC,在射线A ˊ D上截取A ˊ B ˊ =AB;
3.连接B ˊ C ˊ。
(三角形三边相等两三角形全等)
全等
思考
由以上尺规作图的方法可以得到以下基本事实:
两边和它们的夹角分别相等的两个三角形全等。
(即 “ 边角边”或“ SAS”)
小结
在△ABC与△DEF中
AB=DE
∠B=∠E
BC=EF
∴△ABC≌△DEF(SAS)
A
B
C
D
E
F
用语言表达如下:
小结
情况2:两边和其中一边的对角相等,两三角形全等吗?
如图,△ABC与△ABD中,AB=AB,AC=AD,∠B=∠B,他们全等吗?
B
A
C
D
B
A
D
B
A
C
不全等
思考
因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺.请你设计一种方案,粗略测出A、B两杆之间的距离..
分析:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使DC=AC,连结BC并延长至E点,使EC=BC,连结DE,用米尺测出DE的长,这个长度就等于A,B两点的距离.请你说明理由.
AC=DC?
∠ACB=∠DCE
BC=EC
△ACB≌△DCE
AB=DE
对顶角相等
思考
A
B
D
O
1.在下列推理中填写需要补充的条件,使结论成立:
(1)如图,在△AOB和△DOC中
AO=DO(已知)
______=________( )
BO=CO(已知)
∴ △AOB≌△DOC( )
∠ AOB
∠ DOC
对顶角相等
C
SAS
课堂测试
(2)如图,在△AEC和△ADB中,已知AE=AD,AC=AB,请说明△AEC ≌ △ADB的理由。
A
E
B
D
C
____=____(已知)
∠A= ∠A( 公共角)
_____=____(已知)
∴ △AEC≌△ADB( )
AE
AD
AC
AB
解:在△AEC和△ADB中
SAS
课堂测试
(SAS)
A
B
C
D
2.如图,在四边形ABCD中AB=CD,∠ABD= ∠BDC,则AD=BC.请说明理由。
解:在△ABD和△CDB中
AB=CD (已知)
∠ABD= ∠BDC (已知)
(公共边)
∴ △ABD ≌ △CDB
∴ AD= BC( )
BD=DB
全等三角形的对应边相等
课堂测试
A
B
C
D
3.已知:如图AB=CB ,∠ABD=∠CBD ,△ABD和△CBD全等吗?
解:在△ABD和△CBD中
AB=CB (已知)
∠ABD= ∠CBD (已知)
(公共边)
∴ △ABD ≌ △CBD
BD=BD
(SAS)
课堂测试
4.如图,AC=BD,∠CAB=∠DBA,你能判断BC=AD吗?说明理由.
A
B
C
D
解:在△ACB和△BDA中
AC=BD (已知)
∠CAB= ∠DBA (已知)
(公共边)
∴ △ACB≌ △BDA
AB=BA
∴ BC=AD
(SAS)
课堂测试
A
B
C
D
F
E
1.如图,已知AB=DE,AC=DF,要说明△ABC≌△DEF,还需增加一个什么条件?
1.BE = CF (SSS)
2.∠A = ∠D (SAS)
…(答案不唯一)
探索提高
F
C
B
E
D
A
2.如图:己知AD∥BC,AE=CF,AD=BC,E、F都在直线AC上,试说明DE∥BF。
解:在△AED和△CFB中
AE=CF (已知)
∠A=∠C (两直线平行内错角相等)
(已知)
∴ △ AED ≌ △ CFB
AD=BC
∴ ∠D=∠B
∴ ∠D+ ∠A = ∠B+ ∠C 即∠DEF=∠EFB
∴DE∥BF(内错角相等两直线平行)
探索提高
2.如图,AC=BD,∠1= ∠2
求证:BC=AD
变式1: 如图,AC=BD,BC=AD
求证:∠1= ∠2
A
B
C
D
1
2
A
B
C
D
1
2
变式2: 如图,AC=BD,BC=AD
求证:∠C=∠D
A
B
C
D
探索提高
A
B
C
D
变式3: 如图,AC=BD,BC=AD
求证:∠A=∠B
探索提高
感谢各位的仔细聆听
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
