2020-2021学年人教版数学八年级上册12.2.3 三角形全等的判定 (AAS ASA) 课件(19张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册12.2.3 三角形全等的判定 (AAS ASA) 课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 281.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 17:48:02 | ||
图片预览



文档简介
12.2.3 三角形全等的判定 (AAS ASA)
第十二章 全等三角形
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
前 言
学习目标
1.探索并正确理解“ASA”和“AAS”判定方法。
2.会用“ASA”和“AAS”判定方法证明两个三角形全等。
3.通过画图、比较、验证,培养学生注重观察、善于思考、不断总结的良好思维习惯。
重点难点
理解两种判定方法,并掌握用这两种方法证明两个三角形全等。
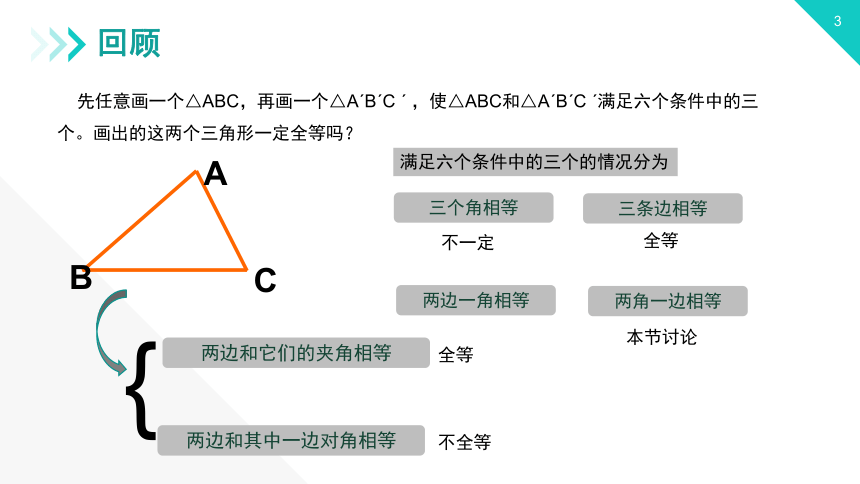
先任意画一个△ABC,再画一个△AˊBˊC ˊ ,使△ABC和△AˊBˊC ˊ满足六个条件中的三个。画出的这两个三角形一定全等吗?
A
B
C
满足六个条件中的三个的情况分为
三个角相等
三条边相等
两边一角相等
两角一边相等
不一定
全等
本节讨论
{
两边和它们的夹角相等
两边和其中一边对角相等
全等
不全等
回顾
两个三角形中两角一边相等的情况分为:
1、两角和他们的夹边分别相等。
2、有两个角和其中一个角的对边相等。
思考
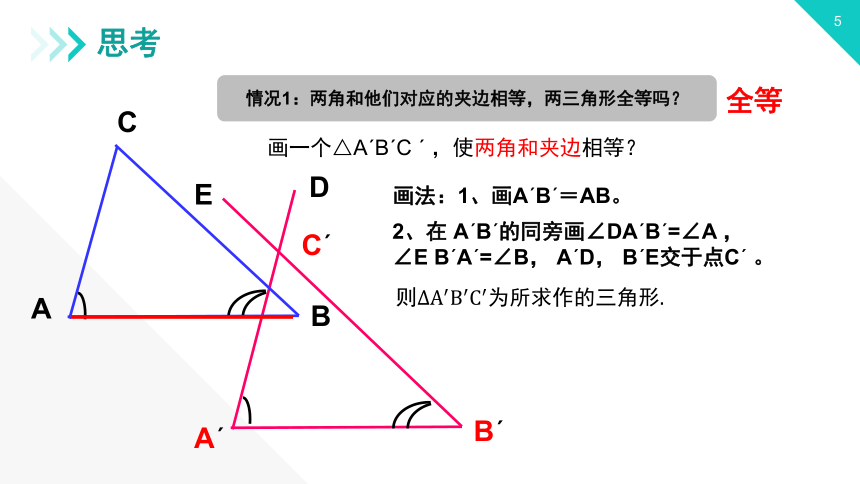
情况1:两角和他们对应的夹边相等,两三角形全等吗?
画一个△AˊBˊC ˊ ,使两角和夹边相等?
则ΔA′B′C′为所求作的三角形.
?
全等
画法:1、画AˊBˊ=AB。
2、在 AˊBˊ的同旁画∠DAˊBˊ=∠A ,
∠E BˊAˊ=∠B, AˊD, BˊE交于点Cˊ 。
Aˊ
Bˊ
E
D
A
C
B
Cˊ
思考
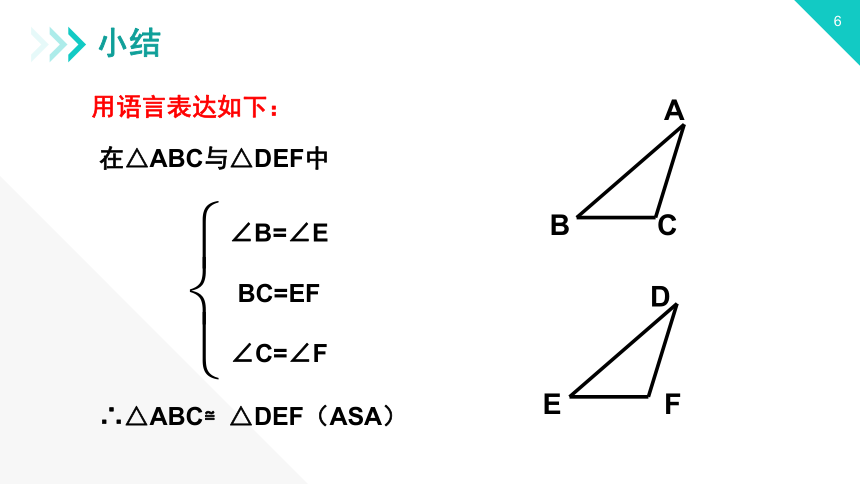
在△ABC与△DEF中
∠B=∠E
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
A
B
C
D
E
F
用语言表达如下:
小结
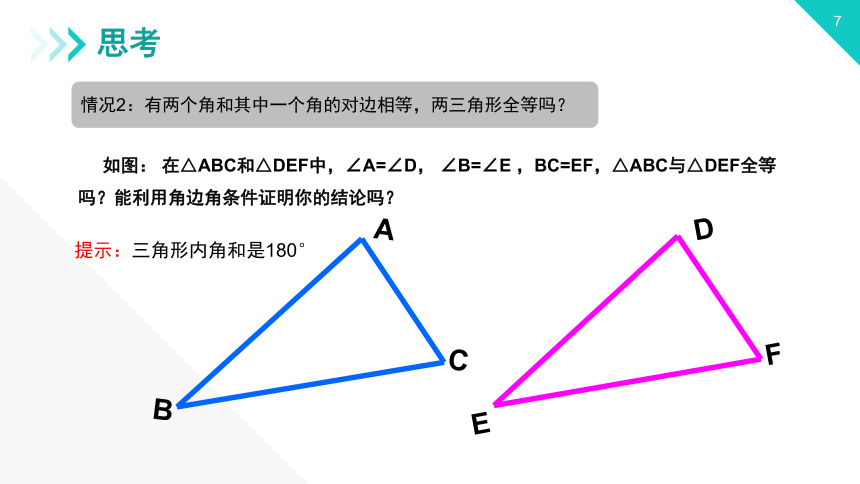
情况2:有两个角和其中一个角的对边相等,两三角形全等吗?
如图: 在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
A
B
C
D
E
F
提示:三角形内角和是180°
思考
证明:
∵ ∠A+∠B+∠C=180o
∠D+∠E+∠F=180o
∴ ∠C=∠F
又∵ ∠A=∠D, ∠B=∠E
在△ABC和△DEF中
∠B=∠E
∠C=∠F
BC=EF
∴ △ABC≌△DEF (ASA)
情况2:有两个角和其中一个角的对边相等,两三角形全等吗?
全等
证明
由以上证明可以得到下面结论:
两角分别相等且其中一组等角的对边相等的两个三角形全等。(即 “ 角角边”或“ AAS”)
小结
在△ABC与△DEF中
∠B=∠E
∠A=∠D
BC=EF
∴△ABC≌△DEF(AAS)
A
B
C
D
E
F
用语言表达如下:
小结
1.如图,O是AB的中点,∠C= ∠D,△AOC与△BOD全等吗?为什么?
O
A
B
C
D
证明:在△AOC和△BOD中,
_____________ ( )
_____________ ( )
_____________ ( )
∴△AOC≌△BOD(AAS)
∠C=∠D
已知条件
∠AOC=∠BOD
对顶角相等
AO=BO
中点定义
课堂测试
2.已知∠1=∠2,∠C=∠D,求证:AD=AC.
证明:在△ABD和△ABC中
∠1=∠2
∠D=∠C
AB=AB
∴△ABD≌△ABC(AAS)
∴AD=AC
1
A
B
C
D
2
课堂测试
∠1=∠2
AB=AB
∠ABD=∠ABC
∴ △ABD≌△ABC(ASA)
∴ AD=AC
3.已知∠1=∠2,∠ABD=∠ABC,求证:AD=AC.
证明:在△ABD和△ABC中
1
A
B
C
D
2
课堂测试
4.如图,E,F 在线段AC上,AD∥CB,AE=CF.若∠B =∠D,
求证:DF=BE.
A
B
C
D
E
F
∠A =∠C(两直线平行内错角相等)
∠D =∠B
AF =CE
∴ △ADF ≌ △CBE (AAS)
∴ DF =BE
证明:在△ADF 和△CBE中,
课堂测试
6.若将条件 “∠B =∠D”变为“DF∥BE”,那么原结论还成立吗?若成立,请证明;若不成立,请说明理由.
A
B
C
D
E
F
课堂测试
1.如图,AC、BD交于点O,AC=BD,AB=CD.
求证:1)∠C= ∠B, 2)OA=OD
A
B
C
D
O
1
2
证明: (1)连接AD, 在△ADC和△DAB中
AD=DA(公共边)
AC=DB(已知)
DC=AB(已知)
∴△ADC≌△DAB (SSS)
∴∠C=∠B(全等三角形的对应角相等)
探索提高
1.如图,AC、BD交于点O,AC=BD,AB=CD.
求证:1)∠C= ∠B, 2)OA=OD
A
B
C
D
O
1
2
(2) 在△ AOB 和△ DOC中
∠ B =∠ C (已证)
∠1=∠2 (对顶角相等)
DC=AB(已知)
∴△DOC≌△AOB (AAS)
∴OA=OD
(全等三角形的对应边相等)
探索提高
=
=
A
B
E
C
F
D
2.如图∠B=∠DEF, BC=EF, 求证:ΔABC≌ ΔDEF
(1)若要以“ SAS”为依据,还缺条件 ______;
(2)若要以“ ASA”为依据,还缺条件______;
(3)若要以“ SSS” 为依据,还缺条件______;
(4)若要以“ AAS” 为依据,还缺条件______;
∠ACB= ∠DEF
AB=DE
AB=DE、AC=DF
∠A=∠D
探索提高
感谢各位的仔细聆听
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
第十二章 全等三角形
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
前 言
学习目标
1.探索并正确理解“ASA”和“AAS”判定方法。
2.会用“ASA”和“AAS”判定方法证明两个三角形全等。
3.通过画图、比较、验证,培养学生注重观察、善于思考、不断总结的良好思维习惯。
重点难点
理解两种判定方法,并掌握用这两种方法证明两个三角形全等。
先任意画一个△ABC,再画一个△AˊBˊC ˊ ,使△ABC和△AˊBˊC ˊ满足六个条件中的三个。画出的这两个三角形一定全等吗?
A
B
C
满足六个条件中的三个的情况分为
三个角相等
三条边相等
两边一角相等
两角一边相等
不一定
全等
本节讨论
{
两边和它们的夹角相等
两边和其中一边对角相等
全等
不全等
回顾
两个三角形中两角一边相等的情况分为:
1、两角和他们的夹边分别相等。
2、有两个角和其中一个角的对边相等。
思考
情况1:两角和他们对应的夹边相等,两三角形全等吗?
画一个△AˊBˊC ˊ ,使两角和夹边相等?
则ΔA′B′C′为所求作的三角形.
?
全等
画法:1、画AˊBˊ=AB。
2、在 AˊBˊ的同旁画∠DAˊBˊ=∠A ,
∠E BˊAˊ=∠B, AˊD, BˊE交于点Cˊ 。
Aˊ
Bˊ
E
D
A
C
B
Cˊ
思考
在△ABC与△DEF中
∠B=∠E
BC=EF
∠C=∠F
∴△ABC≌△DEF(ASA)
A
B
C
D
E
F
用语言表达如下:
小结
情况2:有两个角和其中一个角的对边相等,两三角形全等吗?
如图: 在△ABC和△DEF中,∠A=∠D, ∠B=∠E ,BC=EF,△ABC与△DEF全等吗?能利用角边角条件证明你的结论吗?
A
B
C
D
E
F
提示:三角形内角和是180°
思考
证明:
∵ ∠A+∠B+∠C=180o
∠D+∠E+∠F=180o
∴ ∠C=∠F
又∵ ∠A=∠D, ∠B=∠E
在△ABC和△DEF中
∠B=∠E
∠C=∠F
BC=EF
∴ △ABC≌△DEF (ASA)
情况2:有两个角和其中一个角的对边相等,两三角形全等吗?
全等
证明
由以上证明可以得到下面结论:
两角分别相等且其中一组等角的对边相等的两个三角形全等。(即 “ 角角边”或“ AAS”)
小结
在△ABC与△DEF中
∠B=∠E
∠A=∠D
BC=EF
∴△ABC≌△DEF(AAS)
A
B
C
D
E
F
用语言表达如下:
小结
1.如图,O是AB的中点,∠C= ∠D,△AOC与△BOD全等吗?为什么?
O
A
B
C
D
证明:在△AOC和△BOD中,
_____________ ( )
_____________ ( )
_____________ ( )
∴△AOC≌△BOD(AAS)
∠C=∠D
已知条件
∠AOC=∠BOD
对顶角相等
AO=BO
中点定义
课堂测试
2.已知∠1=∠2,∠C=∠D,求证:AD=AC.
证明:在△ABD和△ABC中
∠1=∠2
∠D=∠C
AB=AB
∴△ABD≌△ABC(AAS)
∴AD=AC
1
A
B
C
D
2
课堂测试
∠1=∠2
AB=AB
∠ABD=∠ABC
∴ △ABD≌△ABC(ASA)
∴ AD=AC
3.已知∠1=∠2,∠ABD=∠ABC,求证:AD=AC.
证明:在△ABD和△ABC中
1
A
B
C
D
2
课堂测试
4.如图,E,F 在线段AC上,AD∥CB,AE=CF.若∠B =∠D,
求证:DF=BE.
A
B
C
D
E
F
∠A =∠C(两直线平行内错角相等)
∠D =∠B
AF =CE
∴ △ADF ≌ △CBE (AAS)
∴ DF =BE
证明:在△ADF 和△CBE中,
课堂测试
6.若将条件 “∠B =∠D”变为“DF∥BE”,那么原结论还成立吗?若成立,请证明;若不成立,请说明理由.
A
B
C
D
E
F
课堂测试
1.如图,AC、BD交于点O,AC=BD,AB=CD.
求证:1)∠C= ∠B, 2)OA=OD
A
B
C
D
O
1
2
证明: (1)连接AD, 在△ADC和△DAB中
AD=DA(公共边)
AC=DB(已知)
DC=AB(已知)
∴△ADC≌△DAB (SSS)
∴∠C=∠B(全等三角形的对应角相等)
探索提高
1.如图,AC、BD交于点O,AC=BD,AB=CD.
求证:1)∠C= ∠B, 2)OA=OD
A
B
C
D
O
1
2
(2) 在△ AOB 和△ DOC中
∠ B =∠ C (已证)
∠1=∠2 (对顶角相等)
DC=AB(已知)
∴△DOC≌△AOB (AAS)
∴OA=OD
(全等三角形的对应边相等)
探索提高
=
=
A
B
E
C
F
D
2.如图∠B=∠DEF, BC=EF, 求证:ΔABC≌ ΔDEF
(1)若要以“ SAS”为依据,还缺条件 ______;
(2)若要以“ ASA”为依据,还缺条件______;
(3)若要以“ SSS” 为依据,还缺条件______;
(4)若要以“ AAS” 为依据,还缺条件______;
∠ACB= ∠DEF
AB=DE
AB=DE、AC=DF
∠A=∠D
探索提高
感谢各位的仔细聆听
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
