河南省豫东、豫北十所名校2012年高三测试(四)数学文
文档属性
| 名称 | 河南省豫东、豫北十所名校2012年高三测试(四)数学文 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-17 00:00:00 | ||
图片预览



文档简介
河南省豫东、豫北十所名校
2012年高中毕业班阶段性测试(四)
数学(文)试题
本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。考生作答时,将答案答在答题卡上(答题注意事项见答题卡),在本试题卷上答题无效。考试结束后,将本试题卷和答题卡一并交回。
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设i是虚数单位,若复数为实数,则实数a为
A.2 B.-2 C.一 D.
2.已知集合A=,R为实数集,则(CRB)A=
A.(-,0) B.(0,1) C.(0,1] D.[1,2)
3.已知等差数列{}的前m项和为Sn,且S3 =6,则5a1+a7,的值为
A.12 B.10 C.24 D.6
4.一个三棱锥和直三棱柱的组合体的直观图以及它的侧(左)视图、俯视图如图所示,则该几何体的正(主)视图为
5.下列命题中,错误的是
A.命题“若,则x=2”的逆否命题是“若x≠2,则”
B.已知x,yR,则成立的充要条件
C.对命题p:则
D.已知命题p和q,若pq为假命题,则命题p与q中必一真一假
6.定义在R上的函数f(x)满足下列三个条件:①对任意的,恒为正值;②;③.则函数只可以是
A. B.
C. D.
7.已知x,y满足不等式组则z=2x +y的最大值与最小值的比值为
A. B. C. D.2
8.对数函数y=logax与二次函数y=(a-l)x2-x在同一坐标系内的图象可能是
9.下表是最近十届奥运会的年份、届别、主办国,以及主办国在上届获得的金牌数、当届获得的金牌数的统计数据:
某体育爱好组织,利用上表研究所获金牌数与主办奥运会之间的关系,求出主办国在上届所获金牌数(设为x)与在当届所获金牌数(设为y)之间的线性回归方程=,在2008年第29届北京奥运会上英国获得19块金牌,则据此线性回归方程估计在2012年第30届伦敦奥运会上英国将获得的金牌数为(所有金牌数精确到整数)
A.29块 B.30块 C.31块 D.32块
10.过双曲线的右焦点F和虚轴端点B(0,6)作一条直线,若右顶点A到直线FB的距离等于,则双曲线的离心率e=
A. B.2 C.或2 D.
11.在△ABC中,a,b,c分别为角A,B,C的对边,如果c=a,B=,那么角C等于
A. B. C. D.
12.已知n为正整数,设抛物线,过点P(2n,0)任作直线l交抛物线于两点,则数列{的前2 012项和是
A.一 B.一 C. D.
第Ⅱ卷
本卷包括必考题和选考题两部分。第13题~第21题为必考题,每个试题考生都必须作答。第22题~第24题为选考题,考生根据要求作答。
二、填空题:本大题共4小题,每小题5分。
13.若函数在区间(1,2)内存在零点,则实数a的取值范围是 。
14.一个四面体中如果有三条棱两两互相垂直,且垂足不是同一点,这三条棱就像中国武术中的兵器——三节棍,所以,我们常把这类四面体称为“三节棍体”,若三节棍体ABCD四个顶点在空间直角坐标系中的坐标分别为A(0,0,0),B(0,2,0),C(2,2,0),D(2,2,2),则此三节棍体外接球的表面积是 。
15.已知等比数列{}为递增数列,且= 。
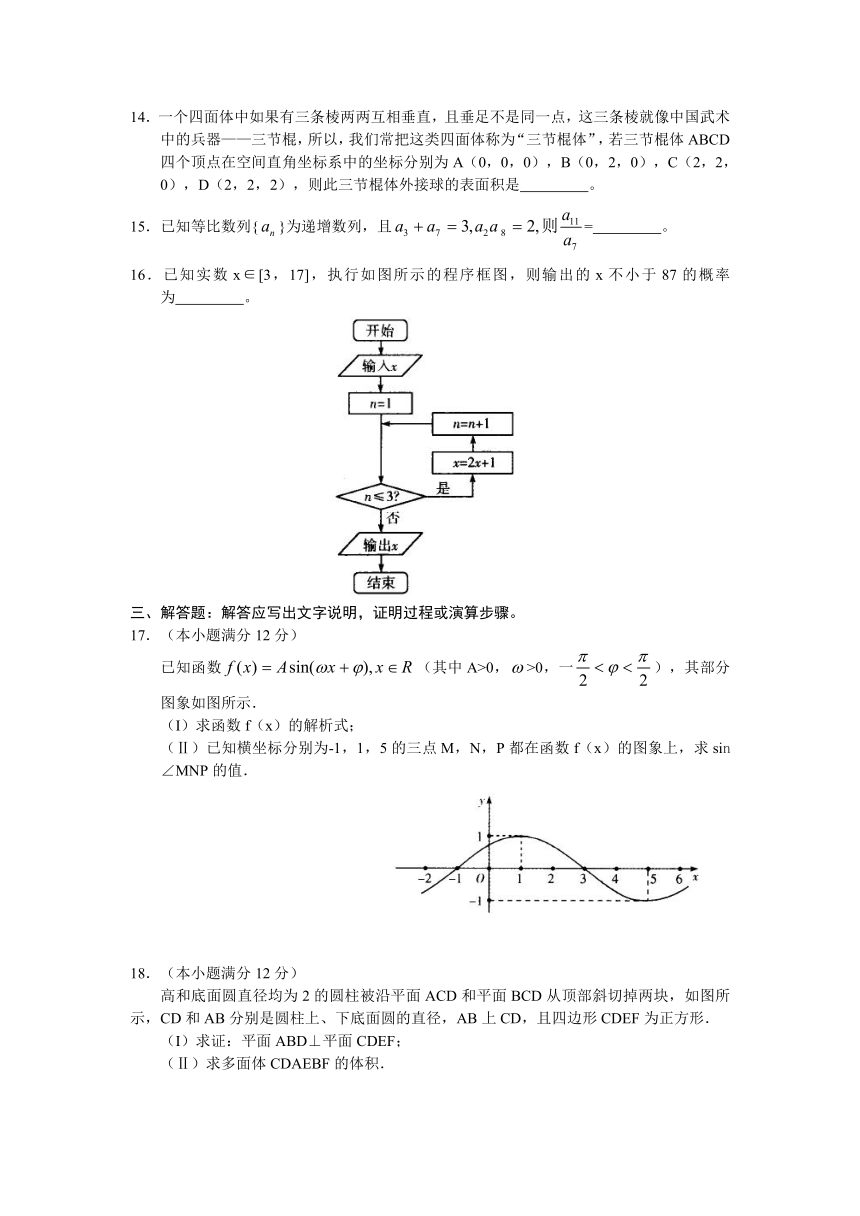
16.已知实数x∈[3,17],执行如图所示的程序框图,则输出的x不小于87的概率为 。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
已知函数(其中A>0,>0,一),其部分图象如图所示.
(I)求函数f(x)的解析式;
(Ⅱ)已知横坐标分别为-1,1,5的三点M,N,P都在函数f(x)的图象上,求sin∠MNP的值.
18.(本小题满分12分)
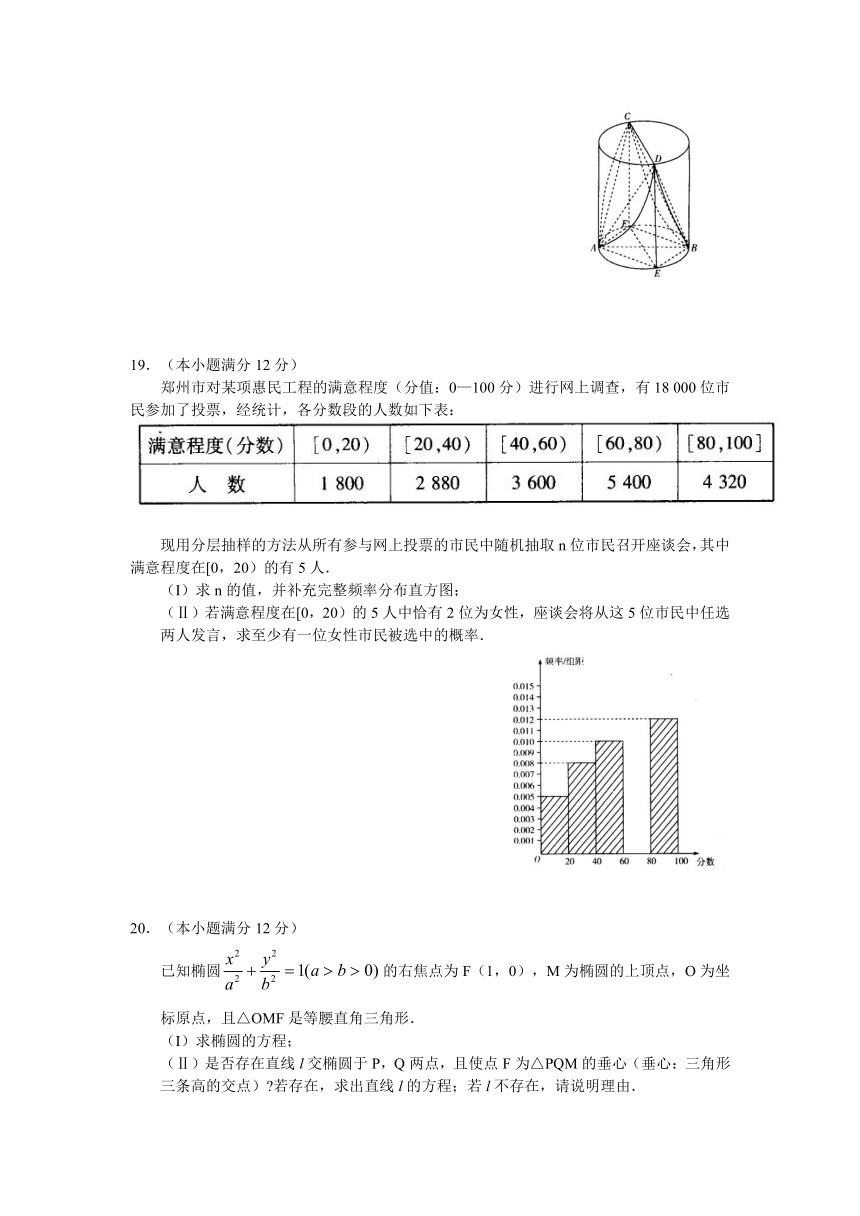
高和底面圆直径均为2的圆柱被沿平面ACD和平面BCD从顶部斜切掉两块,如图所示,CD和AB分别是圆柱上、下底面圆的直径,AB上CD,且四边形CDEF为正方形.
(I)求证:平面ABD⊥平面CDEF;
(Ⅱ)求多面体CDAEBF的体积.
19.(本小题满分12分)
郑州市对某项惠民工程的满意程度(分值:0—100分)进行网上调查,有18 000位市民参加了投票,经统计,各分数段的人数如下表:
现用分层抽样的方法从所有参与网上投票的市民中随机抽取n位市民召开座谈会,其中满意程度在[0,20)的有5人.
(I)求n的值,并补充完整频率分布直方图;
(Ⅱ)若满意程度在[0,20)的5人中恰有2位为女性,座谈会将从这5位市民中任选两人发言,求至少有一位女性市民被选中的概率.
20.(本小题满分12分)
已知椭圆的右焦点为F(1,0),M为椭圆的上顶点,O为坐标原点,且△OMF是等腰直角三角形.
(I)求椭圆的方程;
(Ⅱ)是否存在直线l交椭圆于P,Q两点,且使点F为△PQM的垂心(垂心:三角形三条高的交点) 若存在,求出直线l的方程;若l不存在,请说明理由.
21.(本小题满分12分)
定义:已知函数f(x)与g(x),若存在一条直线y=kx +b,使得对公共定义域内的任意实数均满足g(x)≤f(x)≤kx+b恒成立,其中等号在公共点处成立,则称直线y=kx +b为曲线f(x)与g(x)的“左同旁切线”.已知
(I)证明:直线y=x-l是f(x)与g(x)的“左同旁切线”;
(Ⅱ)设P(是函数 f(x)图象上任意两点,且00,使得.请结合(I)中的结论证明:
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分。作答时请写清题号。
22.(本小题满分10分)选修4-1:几何证明选讲
如图,过半径为4的⊙O上的一点A引半径为3的⊙O′的切线,切点为B,若⊙O与⊙O′内切于点M,连接AM与⊙O′交于c点,求的值.
23.(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知圆锥曲线C的参数方程为为参数).
(I)以原点为极点,x轴正半轴为极轴建立极坐标系,求圆锥曲线C的极坐标方程;
(Ⅱ)若直线l过曲线C的焦点且倾斜角为60°,求直线l被圆锥曲线C所截得的线段的长度.
24.(本小题满分10分)选修4-5:不等式选讲
对定义在区间l,上的函数,若存在开区间和常数C,使得对任意的都有,且对任意的x(a,b)都有恒成立,则称函数为区间I上的“Z型”函数.
(I)求证:函数是R上的“Z型”函数;
(Ⅱ)设是(I)中的“Z型”函数,若不等式对任意的xR恒成立,求实数t的取值范围.
2012年河南省豫东、豫北十所名校高中毕业班阶段性测试(四)
数学(文科)·答案
(1)A (2)C (3)A (4)C (5)D (6)A
(7)D (8)A (9)B (10)B (11)D (12)B
(13)(1,8) (14) (15)2 (16)
(17)解:(Ⅰ)由图可知, 最小正周期 所以
………………………………………………………………………(2分)
又 ,且,
所以,所以…………………………………………(4分)
所以.…………………………………………………………………(5分)
(Ⅱ) 解法一: 因为,
所以,
,……………………………………………………(7分)
从而,……………………………………………………(10分)
由得. …………………………(12分)
解法二: 因为,,
所以, …………………………………………………………(7分)
所以,
又 ,
则. ………………………………………(10分)
由得. …………………………(12分)
(18)解:(Ⅰ)由题意,因为四边形为正方形,可得,所以.又因为,,所以,而,所以.……………………………………………………………(6分)
(Ⅱ)由(Ⅰ)知,是边长为2的正方形,
.………………………………(12分)
(19)解:(Ⅰ)采用分层抽样的方法,样本容量与总体容量的比为,………(1分)
则从满意程度在的投票市民中随机抽取的人数为:,
……………………………………………………………………………………(3分)
补充完整的频率分布直方图如图:…………………………………………………………(5分)
(Ⅱ)由题意知5人中女性2人,男性3人,用表示女性市民,用表示男性市民,事件A表示“至少有一位女性市民被选中发言”.
则从5位市民中任选2位市民发言的基本事件有
,共10个,………………………………………(8分)
其中事件A包含的基本事件有:
,共7个,……………………(10分)
所以.……………………………………………………………………………(12分)
(20)解:(Ⅰ)由△是等腰直角三角形得,,故椭圆方程为…………………………………………………………………………………(4分)
(Ⅱ)假设存在直线交椭圆于,两点,且为△的垂心,设,
因为,,故.………………………………………………………(7分)
于是设直线的方程为,
由得.
由题意知,即,且…………………(9分)
由题意应有又
故,整理得
解得或.经检验,当时,△不存在,故舍去;
当时,所求直线满足题意
综上,存在直线,且直线的方程为.……………………………………(12分)
(21)解:(Ⅰ)要证明结论即证.
令,则,
易知在处取得最大值,所以,即,等号在公共点(1,0)处成立.…………………………………………………………………(2分)
再令,则,易知在处取得最小值,所以,即,等号在公共点(1,0)处成立.…………………………………………………………………………………………(4分)
故对任意,恒有成立,即直线是与的“左同旁切线”.………………………………………………………………………(6分)
(Ⅱ)因为,所以,所以.
…………………………………………………………………………………………………(8分)
解法一:(作差法,利用(Ⅰ)的结论)因为,
,所以.………………(12分)
解法二:(反证法,利用(Ⅰ)的结论)令,则,显然自相矛盾,故;同理可证.故. ………………………………………………………(12分)
(22)解:如图,作两圆的公切线,连接,,则,
所以,………………………………………………………………(3分)
由弦切角定理知,,
则,所以,……………………………………………………(7分)
所以,则.……………………………………(10分)
(23)解:(Ⅰ)曲线的参数方程为(为参数).
所以的普通方程为:. 把代入,得,即,即.…(5分)
(Ⅱ)根据对称性,不妨设直线过曲线的右焦点(1,0),此时直线的参数方程是,代入的普通方程并整理得,所以直线被圆锥曲线所截得的线段的长度为.……………………(10分)
(24)解:(Ⅰ)当时,,此时;
当时,,
当时,,此时.
所以对任意的都有,且对任意的都有恒成立,所以函数为上的“型”函数.…………………………………………………(6分)
(Ⅱ)不等式对一切的恒成立,只要即可,可得或.…………………………………………………………………………………(10分)
2012年高中毕业班阶段性测试(四)
数学(文)试题
本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。考生作答时,将答案答在答题卡上(答题注意事项见答题卡),在本试题卷上答题无效。考试结束后,将本试题卷和答题卡一并交回。
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设i是虚数单位,若复数为实数,则实数a为
A.2 B.-2 C.一 D.
2.已知集合A=,R为实数集,则(CRB)A=
A.(-,0) B.(0,1) C.(0,1] D.[1,2)
3.已知等差数列{}的前m项和为Sn,且S3 =6,则5a1+a7,的值为
A.12 B.10 C.24 D.6
4.一个三棱锥和直三棱柱的组合体的直观图以及它的侧(左)视图、俯视图如图所示,则该几何体的正(主)视图为
5.下列命题中,错误的是
A.命题“若,则x=2”的逆否命题是“若x≠2,则”
B.已知x,yR,则成立的充要条件
C.对命题p:则
D.已知命题p和q,若pq为假命题,则命题p与q中必一真一假
6.定义在R上的函数f(x)满足下列三个条件:①对任意的,恒为正值;②;③.则函数只可以是
A. B.
C. D.
7.已知x,y满足不等式组则z=2x +y的最大值与最小值的比值为
A. B. C. D.2
8.对数函数y=logax与二次函数y=(a-l)x2-x在同一坐标系内的图象可能是
9.下表是最近十届奥运会的年份、届别、主办国,以及主办国在上届获得的金牌数、当届获得的金牌数的统计数据:
某体育爱好组织,利用上表研究所获金牌数与主办奥运会之间的关系,求出主办国在上届所获金牌数(设为x)与在当届所获金牌数(设为y)之间的线性回归方程=,在2008年第29届北京奥运会上英国获得19块金牌,则据此线性回归方程估计在2012年第30届伦敦奥运会上英国将获得的金牌数为(所有金牌数精确到整数)
A.29块 B.30块 C.31块 D.32块
10.过双曲线的右焦点F和虚轴端点B(0,6)作一条直线,若右顶点A到直线FB的距离等于,则双曲线的离心率e=
A. B.2 C.或2 D.
11.在△ABC中,a,b,c分别为角A,B,C的对边,如果c=a,B=,那么角C等于
A. B. C. D.
12.已知n为正整数,设抛物线,过点P(2n,0)任作直线l交抛物线于两点,则数列{的前2 012项和是
A.一 B.一 C. D.
第Ⅱ卷
本卷包括必考题和选考题两部分。第13题~第21题为必考题,每个试题考生都必须作答。第22题~第24题为选考题,考生根据要求作答。
二、填空题:本大题共4小题,每小题5分。
13.若函数在区间(1,2)内存在零点,则实数a的取值范围是 。
14.一个四面体中如果有三条棱两两互相垂直,且垂足不是同一点,这三条棱就像中国武术中的兵器——三节棍,所以,我们常把这类四面体称为“三节棍体”,若三节棍体ABCD四个顶点在空间直角坐标系中的坐标分别为A(0,0,0),B(0,2,0),C(2,2,0),D(2,2,2),则此三节棍体外接球的表面积是 。
15.已知等比数列{}为递增数列,且= 。
16.已知实数x∈[3,17],执行如图所示的程序框图,则输出的x不小于87的概率为 。
三、解答题:解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分12分)
已知函数(其中A>0,>0,一),其部分图象如图所示.
(I)求函数f(x)的解析式;
(Ⅱ)已知横坐标分别为-1,1,5的三点M,N,P都在函数f(x)的图象上,求sin∠MNP的值.
18.(本小题满分12分)
高和底面圆直径均为2的圆柱被沿平面ACD和平面BCD从顶部斜切掉两块,如图所示,CD和AB分别是圆柱上、下底面圆的直径,AB上CD,且四边形CDEF为正方形.
(I)求证:平面ABD⊥平面CDEF;
(Ⅱ)求多面体CDAEBF的体积.
19.(本小题满分12分)
郑州市对某项惠民工程的满意程度(分值:0—100分)进行网上调查,有18 000位市民参加了投票,经统计,各分数段的人数如下表:
现用分层抽样的方法从所有参与网上投票的市民中随机抽取n位市民召开座谈会,其中满意程度在[0,20)的有5人.
(I)求n的值,并补充完整频率分布直方图;
(Ⅱ)若满意程度在[0,20)的5人中恰有2位为女性,座谈会将从这5位市民中任选两人发言,求至少有一位女性市民被选中的概率.
20.(本小题满分12分)
已知椭圆的右焦点为F(1,0),M为椭圆的上顶点,O为坐标原点,且△OMF是等腰直角三角形.
(I)求椭圆的方程;
(Ⅱ)是否存在直线l交椭圆于P,Q两点,且使点F为△PQM的垂心(垂心:三角形三条高的交点) 若存在,求出直线l的方程;若l不存在,请说明理由.
21.(本小题满分12分)
定义:已知函数f(x)与g(x),若存在一条直线y=kx +b,使得对公共定义域内的任意实数均满足g(x)≤f(x)≤kx+b恒成立,其中等号在公共点处成立,则称直线y=kx +b为曲线f(x)与g(x)的“左同旁切线”.已知
(I)证明:直线y=x-l是f(x)与g(x)的“左同旁切线”;
(Ⅱ)设P(是函数 f(x)图象上任意两点,且0
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分。作答时请写清题号。
22.(本小题满分10分)选修4-1:几何证明选讲
如图,过半径为4的⊙O上的一点A引半径为3的⊙O′的切线,切点为B,若⊙O与⊙O′内切于点M,连接AM与⊙O′交于c点,求的值.
23.(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知圆锥曲线C的参数方程为为参数).
(I)以原点为极点,x轴正半轴为极轴建立极坐标系,求圆锥曲线C的极坐标方程;
(Ⅱ)若直线l过曲线C的焦点且倾斜角为60°,求直线l被圆锥曲线C所截得的线段的长度.
24.(本小题满分10分)选修4-5:不等式选讲
对定义在区间l,上的函数,若存在开区间和常数C,使得对任意的都有,且对任意的x(a,b)都有恒成立,则称函数为区间I上的“Z型”函数.
(I)求证:函数是R上的“Z型”函数;
(Ⅱ)设是(I)中的“Z型”函数,若不等式对任意的xR恒成立,求实数t的取值范围.
2012年河南省豫东、豫北十所名校高中毕业班阶段性测试(四)
数学(文科)·答案
(1)A (2)C (3)A (4)C (5)D (6)A
(7)D (8)A (9)B (10)B (11)D (12)B
(13)(1,8) (14) (15)2 (16)
(17)解:(Ⅰ)由图可知, 最小正周期 所以
………………………………………………………………………(2分)
又 ,且,
所以,所以…………………………………………(4分)
所以.…………………………………………………………………(5分)
(Ⅱ) 解法一: 因为,
所以,
,……………………………………………………(7分)
从而,……………………………………………………(10分)
由得. …………………………(12分)
解法二: 因为,,
所以, …………………………………………………………(7分)
所以,
又 ,
则. ………………………………………(10分)
由得. …………………………(12分)
(18)解:(Ⅰ)由题意,因为四边形为正方形,可得,所以.又因为,,所以,而,所以.……………………………………………………………(6分)
(Ⅱ)由(Ⅰ)知,是边长为2的正方形,
.………………………………(12分)
(19)解:(Ⅰ)采用分层抽样的方法,样本容量与总体容量的比为,………(1分)
则从满意程度在的投票市民中随机抽取的人数为:,
……………………………………………………………………………………(3分)
补充完整的频率分布直方图如图:…………………………………………………………(5分)
(Ⅱ)由题意知5人中女性2人,男性3人,用表示女性市民,用表示男性市民,事件A表示“至少有一位女性市民被选中发言”.
则从5位市民中任选2位市民发言的基本事件有
,共10个,………………………………………(8分)
其中事件A包含的基本事件有:
,共7个,……………………(10分)
所以.……………………………………………………………………………(12分)
(20)解:(Ⅰ)由△是等腰直角三角形得,,故椭圆方程为…………………………………………………………………………………(4分)
(Ⅱ)假设存在直线交椭圆于,两点,且为△的垂心,设,
因为,,故.………………………………………………………(7分)
于是设直线的方程为,
由得.
由题意知,即,且…………………(9分)
由题意应有又
故,整理得
解得或.经检验,当时,△不存在,故舍去;
当时,所求直线满足题意
综上,存在直线,且直线的方程为.……………………………………(12分)
(21)解:(Ⅰ)要证明结论即证.
令,则,
易知在处取得最大值,所以,即,等号在公共点(1,0)处成立.…………………………………………………………………(2分)
再令,则,易知在处取得最小值,所以,即,等号在公共点(1,0)处成立.…………………………………………………………………………………………(4分)
故对任意,恒有成立,即直线是与的“左同旁切线”.………………………………………………………………………(6分)
(Ⅱ)因为,所以,所以.
…………………………………………………………………………………………………(8分)
解法一:(作差法,利用(Ⅰ)的结论)因为,
,所以.………………(12分)
解法二:(反证法,利用(Ⅰ)的结论)令,则,显然自相矛盾,故;同理可证.故. ………………………………………………………(12分)
(22)解:如图,作两圆的公切线,连接,,则,
所以,………………………………………………………………(3分)
由弦切角定理知,,
则,所以,……………………………………………………(7分)
所以,则.……………………………………(10分)
(23)解:(Ⅰ)曲线的参数方程为(为参数).
所以的普通方程为:. 把代入,得,即,即.…(5分)
(Ⅱ)根据对称性,不妨设直线过曲线的右焦点(1,0),此时直线的参数方程是,代入的普通方程并整理得,所以直线被圆锥曲线所截得的线段的长度为.……………………(10分)
(24)解:(Ⅰ)当时,,此时;
当时,,
当时,,此时.
所以对任意的都有,且对任意的都有恒成立,所以函数为上的“型”函数.…………………………………………………(6分)
(Ⅱ)不等式对一切的恒成立,只要即可,可得或.…………………………………………………………………………………(10分)
同课章节目录
