吉林省通化县高中2020-2021学年高一下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 吉林省通化县高中2020-2021学年高一下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 496.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 12:03:04 | ||
图片预览



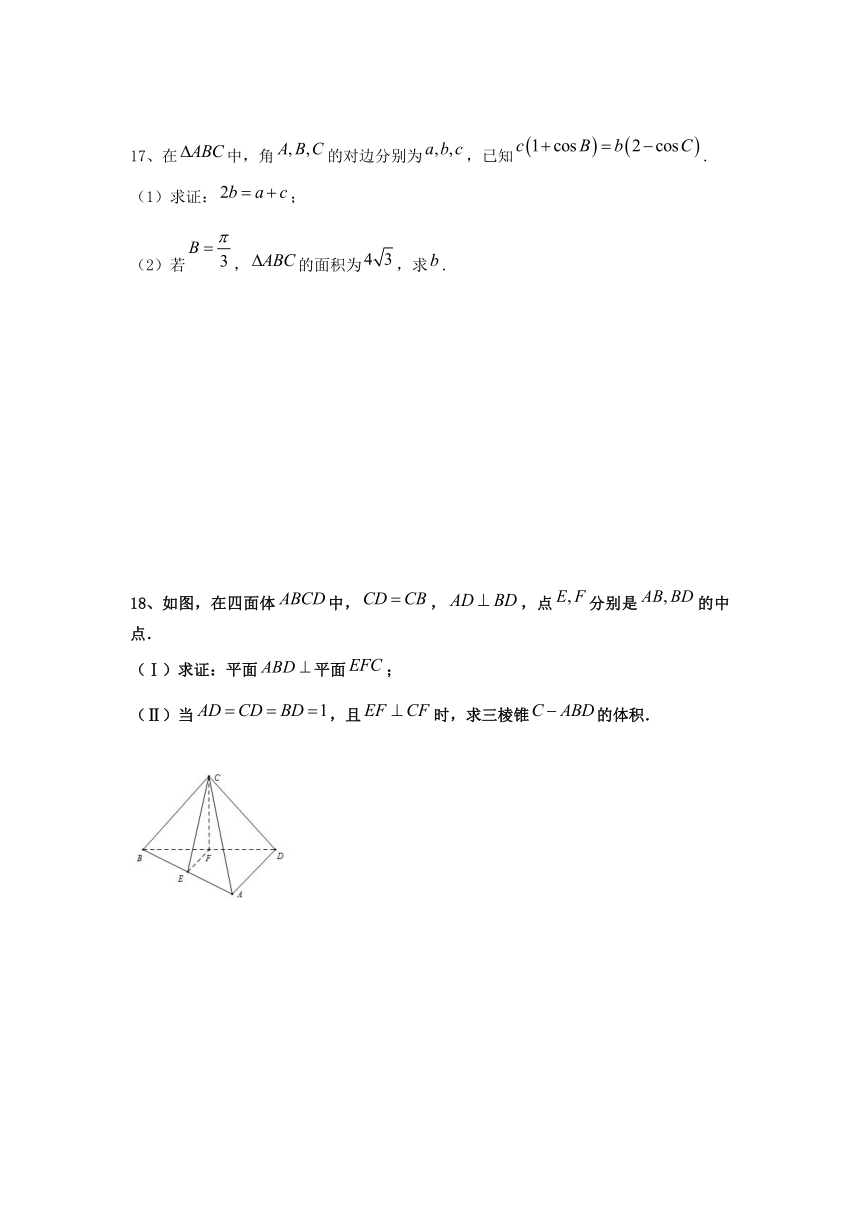
文档简介
通化县高中2020-2021学年高一下学期期末考试
数学试卷
注意事项:
一、单项选择(共10道题,每题4分,共40分)
1、复数( )
A. B. C. D.
2、在平行四边形ABCD中,设对角线AC与BD相交于点O,则( )
A. B. C. D.
3、在中,,,,则为( )
A. B. C. D.
4、复数(为虚数单位),则等于( )
A.3 B. C.2 D.
设、是两条不同的直线,、是两个不同的平面,则下列命题中正确的是( )
若平行于内的无数条直线,则
若,,则平行于内的无数条直线
C.若,,,则
D.若,,则
6、三棱柱的底面是正三角形,侧棱垂直于底面,它的侧面展开图是边长分别为6和4的矩形,则它的体积为( )
A. B. C.或 D.或
7、从分别写有的张卡片中,任取张,这张上的字母恰好按字母顺序相邻的概率为( )
A. B. C. D.
8、在中,点在边上,点在边上,且,,若,,则( )
A. B. C. D.
9、已知某地区中小学生人数和近视情况分别如图1和图2所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取的学生进行调查,则样本容量和抽取的初中生近视人数分别为( )
A.100,90 B.200,27 C.200,20 D.200,90
10、已知正方体的棱长为2.它的8个顶点都在一个球面上,则此球的表面积是( )
A.8π B.12π C.16π D.20π
填空题(共4题,每题5分,共20分)
某校高三数学组有5名党员教师,他们一天中在学习强国平台上的学习积分依次为35,
35,40,38,52,则这5名党员教师学习积分的方差为_______________
12、在中,边,角,则边_____________.
13、已知事件互相对立,且,则=_____.
14、三棱柱的侧棱垂直于底面,且,若该三
棱柱的所有顶点都在同一球面上,则该球的表面积为____________.
三、解答题(共5题,每题12分,共60分)
15、如图,在长方体中,,,点P为棱的中点.
(1)证明:平面PAC;
(2)求异面直线与AP所成角的大小.
16、已知,.
(1)若为与的夹角,求的值;
(2)若与垂直,求的值.
17、在中,角的对边分别为,已知.
(1)求证:;
(2)若,的面积为,求.
如图,在四面体中,,,点分别是的中点.
(Ⅰ)求证:平面平面;
(Ⅱ)当,且时,求三棱锥的体积.
19、哈尔滨市第三中学校响应教育部门疫情期间“停课不停学”的号召,实施网络授课,为检验学生上网课的效果,高三学年进行了一次网络模拟考试.全学年共1500人,现从中抽取了100人的数学成绩,绘制成频率分布直方图(如下图所示).已知这100人中分数段的人数比分数段的人数多6人.
(1)根据频率分布直方图,求a,b的值,并估计抽取的100名同学数学成绩的中位数;
(2)现用分层抽样的方法从分数在,的两组同学中随机抽取6名同学,从这6名同学中再任选2名同学作为“网络课堂学习优秀代表”发言,求这2名同学的分数不在同一组内的概率.
通化县高中2020-2021学年高一下学期期末考试
数学答案参考答案
一、单项选择
1、【答案】B
2、【答案】B
3、【答案】A
4、【答案】D
5、【答案】B
6、【答案】D
7、【答案】B
8、【答案】A
9、【答案】B
10、【答案】B
二、填空题
11、【答案】;
12、【答案】
13、【答案】
14、【答案】
三、解答题
15、【答案】(1)证明见解析;(2).
【解析】(1)证明:设AC和BD交于点O,则O为BD的中点...............2分
连结PO,又因为P是的中点,所以.......................3分
又因为平面PAC,平面PAC................................5分
所以直线平面PAC..............................................6分
(2)解:由(1)知,,所以即为异面直线与AP所成的角或其补角................................................................9分
因为,且,
所以......................................10分
又,所以.................................11分
故异面直线与AP所成角的大小为................................12分
16【答案】(1);(2);
试题分析:(1)因为,,求得,,根据,即可求得答案;
(2)因为与垂直,可得,结合已知条件,即可求得答案.
详解:(1),,
,,..........................2分
...................4分
................................................6分
(2),
,...................8分
与垂直
,...............................10分
,
解得:............................................12分
17、【答案】(1)证明见解析;(2).
试题分析:(1)由正弦定理边化角统一角,得,再用正弦定理角化边即证.(2)由角B的面积公式可得.结合(1)中和解B的余弦定理,三个方程三个未知数,可解得b.
试题解析:(1)∵.
∴由正弦定理可得:,...........2分
可得:,
∴............................................4分
∴.....................................................6分
(2)∵,的面积为,...........8分
∴
∴......................................................9分
∵由余弦定理可得:....10分
∵,
∴可得:,............................................11分
解得:..........................................................12分
18、【答案】(1)见解析(2)
试题分析:(I)由CB=CD得CF⊥BD,由AD⊥BD,AD∥EF得EF⊥BD,故BD⊥平面CEF,于是平面ABD⊥平面EFC;
(II)由CF⊥BD,CF⊥EF得CF⊥平面ABD,即CF为棱锥的高.底面为直角△ABD,代入体积公式计算即可.
详解:(Ⅰ)证明:∵中,分别是的中点,.....1分
,................................................2分中,,是的中点,
.,...........................................4分
面,平面........................................5分
平面平面;................................................6分
(Ⅱ)解:,是的中点,,,,
∴平面,.....................................................2分
,,,,.........3分
,.........................................................4分
...........................................6分
19、【答案】(1),;中位数为;(2).
(1)由频率分布直方图的面积和为1,则
,得. 2分
又由100人中分数段的人数比分数段的人数多6人
则,解得,............................4分
中位数中位数为..........6分
(2)设“抽取的2名同学的分数不在同一组内”为事件A,
由题意知,在分数为的同学中抽取4人,分别用,,,表示,
在分数为的同学中抽取2人,分别用,表示..................7分
从这6名同学中抽取2人所有可能出现的结果有:
,,,,,,,,,,,,,,,共15种............9分
抽取的2名同学的分数不在同一组内的结果有:,,,,,,,,共8种.............................11分
所以抽取的2名同学的分数不在同一组内的概率为..............12分
数学试卷
注意事项:
一、单项选择(共10道题,每题4分,共40分)
1、复数( )
A. B. C. D.
2、在平行四边形ABCD中,设对角线AC与BD相交于点O,则( )
A. B. C. D.
3、在中,,,,则为( )
A. B. C. D.
4、复数(为虚数单位),则等于( )
A.3 B. C.2 D.
设、是两条不同的直线,、是两个不同的平面,则下列命题中正确的是( )
若平行于内的无数条直线,则
若,,则平行于内的无数条直线
C.若,,,则
D.若,,则
6、三棱柱的底面是正三角形,侧棱垂直于底面,它的侧面展开图是边长分别为6和4的矩形,则它的体积为( )
A. B. C.或 D.或
7、从分别写有的张卡片中,任取张,这张上的字母恰好按字母顺序相邻的概率为( )
A. B. C. D.
8、在中,点在边上,点在边上,且,,若,,则( )
A. B. C. D.
9、已知某地区中小学生人数和近视情况分别如图1和图2所示.为了解该地区中小学生的近视形成原因,用分层抽样的方法抽取的学生进行调查,则样本容量和抽取的初中生近视人数分别为( )
A.100,90 B.200,27 C.200,20 D.200,90
10、已知正方体的棱长为2.它的8个顶点都在一个球面上,则此球的表面积是( )
A.8π B.12π C.16π D.20π
填空题(共4题,每题5分,共20分)
某校高三数学组有5名党员教师,他们一天中在学习强国平台上的学习积分依次为35,
35,40,38,52,则这5名党员教师学习积分的方差为_______________
12、在中,边,角,则边_____________.
13、已知事件互相对立,且,则=_____.
14、三棱柱的侧棱垂直于底面,且,若该三
棱柱的所有顶点都在同一球面上,则该球的表面积为____________.
三、解答题(共5题,每题12分,共60分)
15、如图,在长方体中,,,点P为棱的中点.
(1)证明:平面PAC;
(2)求异面直线与AP所成角的大小.
16、已知,.
(1)若为与的夹角,求的值;
(2)若与垂直,求的值.
17、在中,角的对边分别为,已知.
(1)求证:;
(2)若,的面积为,求.
如图,在四面体中,,,点分别是的中点.
(Ⅰ)求证:平面平面;
(Ⅱ)当,且时,求三棱锥的体积.
19、哈尔滨市第三中学校响应教育部门疫情期间“停课不停学”的号召,实施网络授课,为检验学生上网课的效果,高三学年进行了一次网络模拟考试.全学年共1500人,现从中抽取了100人的数学成绩,绘制成频率分布直方图(如下图所示).已知这100人中分数段的人数比分数段的人数多6人.
(1)根据频率分布直方图,求a,b的值,并估计抽取的100名同学数学成绩的中位数;
(2)现用分层抽样的方法从分数在,的两组同学中随机抽取6名同学,从这6名同学中再任选2名同学作为“网络课堂学习优秀代表”发言,求这2名同学的分数不在同一组内的概率.
通化县高中2020-2021学年高一下学期期末考试
数学答案参考答案
一、单项选择
1、【答案】B
2、【答案】B
3、【答案】A
4、【答案】D
5、【答案】B
6、【答案】D
7、【答案】B
8、【答案】A
9、【答案】B
10、【答案】B
二、填空题
11、【答案】;
12、【答案】
13、【答案】
14、【答案】
三、解答题
15、【答案】(1)证明见解析;(2).
【解析】(1)证明:设AC和BD交于点O,则O为BD的中点...............2分
连结PO,又因为P是的中点,所以.......................3分
又因为平面PAC,平面PAC................................5分
所以直线平面PAC..............................................6分
(2)解:由(1)知,,所以即为异面直线与AP所成的角或其补角................................................................9分
因为,且,
所以......................................10分
又,所以.................................11分
故异面直线与AP所成角的大小为................................12分
16【答案】(1);(2);
试题分析:(1)因为,,求得,,根据,即可求得答案;
(2)因为与垂直,可得,结合已知条件,即可求得答案.
详解:(1),,
,,..........................2分
...................4分
................................................6分
(2),
,...................8分
与垂直
,...............................10分
,
解得:............................................12分
17、【答案】(1)证明见解析;(2).
试题分析:(1)由正弦定理边化角统一角,得,再用正弦定理角化边即证.(2)由角B的面积公式可得.结合(1)中和解B的余弦定理,三个方程三个未知数,可解得b.
试题解析:(1)∵.
∴由正弦定理可得:,...........2分
可得:,
∴............................................4分
∴.....................................................6分
(2)∵,的面积为,...........8分
∴
∴......................................................9分
∵由余弦定理可得:....10分
∵,
∴可得:,............................................11分
解得:..........................................................12分
18、【答案】(1)见解析(2)
试题分析:(I)由CB=CD得CF⊥BD,由AD⊥BD,AD∥EF得EF⊥BD,故BD⊥平面CEF,于是平面ABD⊥平面EFC;
(II)由CF⊥BD,CF⊥EF得CF⊥平面ABD,即CF为棱锥的高.底面为直角△ABD,代入体积公式计算即可.
详解:(Ⅰ)证明:∵中,分别是的中点,.....1分
,................................................2分中,,是的中点,
.,...........................................4分
面,平面........................................5分
平面平面;................................................6分
(Ⅱ)解:,是的中点,,,,
∴平面,.....................................................2分
,,,,.........3分
,.........................................................4分
...........................................6分
19、【答案】(1),;中位数为;(2).
(1)由频率分布直方图的面积和为1,则
,得. 2分
又由100人中分数段的人数比分数段的人数多6人
则,解得,............................4分
中位数中位数为..........6分
(2)设“抽取的2名同学的分数不在同一组内”为事件A,
由题意知,在分数为的同学中抽取4人,分别用,,,表示,
在分数为的同学中抽取2人,分别用,表示..................7分
从这6名同学中抽取2人所有可能出现的结果有:
,,,,,,,,,,,,,,,共15种............9分
抽取的2名同学的分数不在同一组内的结果有:,,,,,,,,共8种.............................11分
所以抽取的2名同学的分数不在同一组内的概率为..............12分
同课章节目录
