江苏省南京29中2022届高三上学期7月摸底考试数学试题 PDF版含答案
文档属性
| 名称 | 江苏省南京29中2022届高三上学期7月摸底考试数学试题 PDF版含答案 |  | |
| 格式 | |||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 12:51:58 | ||
图片预览




文档简介
南京二十九中 2022 届高三摸底调研测试
数 学 试 题
注意事项:
1.本卷共6页,包括22小题,满分150分,考试时间120分钟。答卷前,考生务
必将自己的姓名、准考证号等填写在答题卡的指定位置上并准确粘贴条形码。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂
黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在
答题卡上。写在本试卷上无效。
3.考试结束后,将答题卡交回。
一、单项选择题(本大题共 8 小题,每小题 5 分,共 40 分;每题只有一个
选项符合题意)
1. 集合 ,则(CRM)∩N=
A. B. C. D.
2. 是 的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
3. 如图,放置的边长为 1 的正方形 PABC 沿 x轴滚动,点 B 恰好经过原点,
设顶点 的轨迹方程是 ,则对函数 有下列命题:
若 ,则函数 是偶函数; 对任意的 ,都有
; 函数 在区间 上单调递减; 函数
在区间 上是减函数.其中真命题的序号是
A. B. C. D.
4. 声强级 单位: 与声强I的函数关系式为: 若普通列
车的声强级是 95dB,高速列车的声强级为 45dB,则普通列车的声强是
高速列车声强的
A. 倍 B. 倍 C. 倍 D. 倍
5. 某艺术爱好者对 蒙娜丽莎 的同比例影像作品进行了测绘。将画中女
子的嘴唇近似看作一个圆弧,在嘴角A,C 处作圆弧的切线,两条切线
交于 B点,测得如下数据: , , 根
据测量得到的结果推算女子的嘴唇视作的圆弧对应的圆心角位于
1
A. B. C. D.
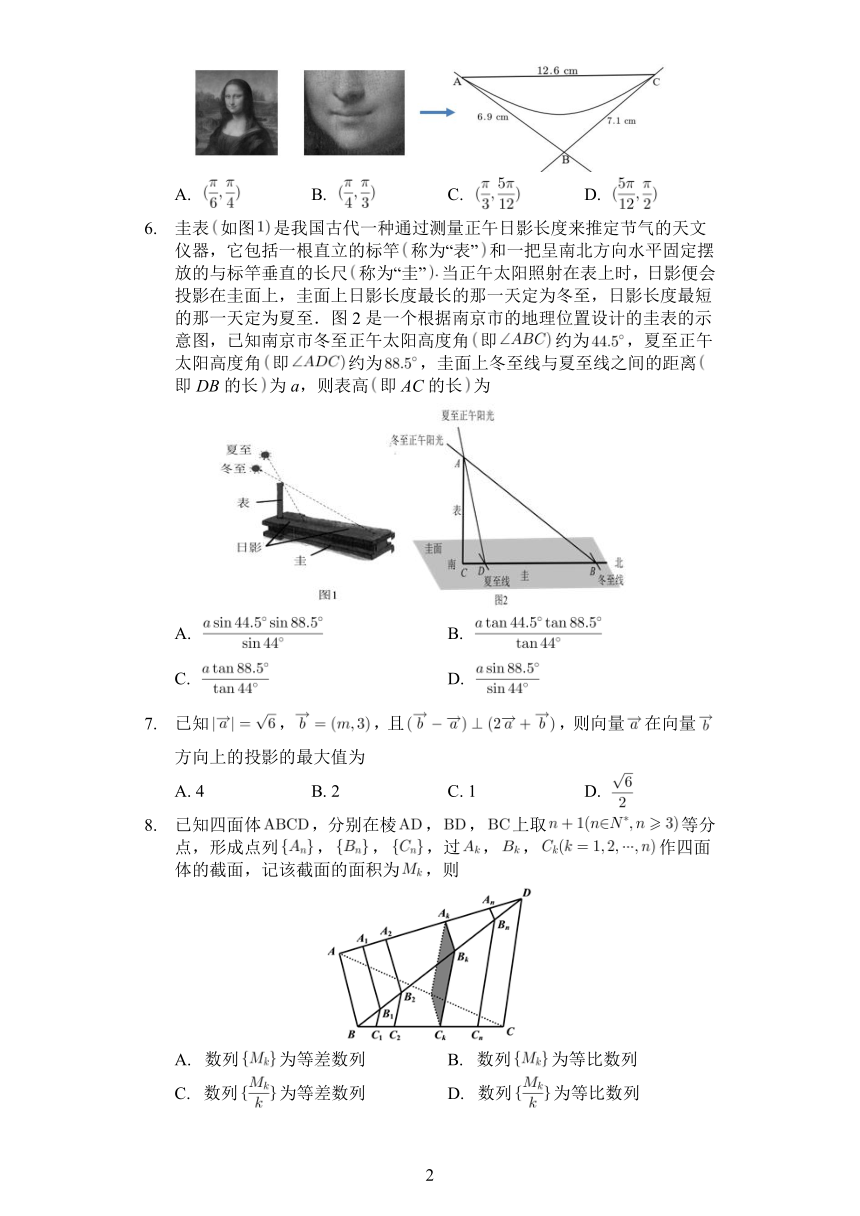
6. 圭表 如图 是我国古代一种通过测量正午日影长度来推定节气的天文
仪器,它包括一根直立的标竿 称为“表” 和一把呈南北方向水平固定摆
放的与标竿垂直的长尺 称为“圭” 当正午太阳照射在表上时,日影便会
投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短
的那一天定为夏至.图 2 是一个根据南京市的地理位置设计的圭表的示
意图,已知南京市冬至正午太阳高度角 即 约为 ,夏至正午
太阳高度角 即 约为 ,圭面上冬至线与夏至线之间的距离
即 DB 的长 为 a,则表高 即 AC 的长 为
A. B.
C. D.
7. 已知 , ,且 ,则向量 在向量
方向上的投影的最大值为
A. 4 B. 2 C. 1 D.
8. 已知四面体 ,分别在棱 , , 上取 等分
点,形成点列 , , ,过 , , 作四面
体的截面,记该截面的面积为 ,则
A. 数列 为等差数列 B. 数列 为等比数列
C. 数列 为等差数列 D. 数列 为等比数列
2
二、多项选择题(本大题共 4 小题,每小题 5 分,共 20 分;每题全选且正
确得 5 分,部分选择且正确的得2 分,有选错的得 0 分)
9. 函数 ,若 在 和 处切线平行,则
A. B. C. D.
10. 分别是双曲线 的左、右焦点,A 为左顶点,P
为双曲线右支上一点,若 且 的最小内角为 ,则
A. 双曲线的离心率
B. 双曲线的渐近线方程为
C.
D. 直线 与双曲线有两个公共点
11. 甲罐中有 3 个红球、2 个白球,乙罐中有 4 个红球、1 个白球,先从甲罐
中随机取出 1 个球放入乙罐,分别以 , 表示由甲罐中取出的球是红
球、白球的事件,再从乙罐中随机取出1 个球,以 B表示从乙罐中取出
的球是红球的事件,下列判断正确的是
A. B. 事件 B 与事件 相互独立
C. 事件 B 与事件 相互独立 D. , 互斥
12. 如图,在矩形 ABCD中, ,E 为 AB 的中点,将 沿
DE 翻折到 的位置, 平面 ABCD,M为 的中点,则在翻折
过程中,下列结论正确的是
A. 平面
B. B 与 M两点间距离为定值
C. 三棱锥 的体积的最大值为
D. 存在某个位置,使得平面 平面
三、填空题(本大题共 4 小题,每小题 5 分,共 20 分)
13. 已知复数 z 满足 ,且 其中 i 是虚数单位 ,则复数
▲ .
14. 剪纸社团某学生剪出了三个互相外切的圆,其半径分别为 , ,
单位: ,则三个圆之间空隙部分的面积为 ▲ .
15. 过抛物线 C: 的准线上任意一点 P作抛物线 C 的切线 PA,PB,
切点分别为 A,B,则点 A 到准线的距离与点 B 到准线的距离之和的最小
值是 ▲ .
3
16. 已知向量 , 满足 , ,若存在不同的实数 , ,
使得 ,且 ,则 的
取值范围是 ▲ .
四、解答题(本大题共 6 小题,第 17 题满分 10 分,其余每题满分 12 分,
共 70 分)
17. 在 中,设 A、B、C 所对的边分别为 a、b、c,已知 ,
且三角形外接圆半径为 .
(1)若 的面积为 ,求 的值;
(2)设 的外接圆圆心为 O,且满足 ,
求 m的值.
18. 已知 为等差数列, 为等比数列, , ,
.
1 求 和 的通项公式;
2 对任意的正整数 n,设 ,求数列 的前
2n 项和.
4
19. 如图,等腰直角三角形 ABC 所在的平面与半圆弧 AB所在的平面垂直,
,P是弧 AB 上一点,且 .
证明:平面 平面 ACP;
若 Q是弧 AP 上异于 A,P的一个动点,且 ,当三棱锥
体积最大时,求点 A到平面 PCQ的距离.
20. 某在外务工人员甲不知自己已感染新冠病毒(处于潜伏期),他从疫区
回乡过春节,这期间他和乙、丙、丁三位朋友相聚。最终,乙、丙、丁
也感染了新冠病毒.此时,乙被肯定是受甲感染,丙是受甲或乙感染的。
假设他受甲和受乙感染的概率分别是 和 丁是受甲、乙或丙感染的,
假设他受甲、乙和丙感染的概率分别是 、 和 在这种假设之下,
乙、丙、丁中直接受甲感染的人数为X.
求 X的分布列和数学期望;
该市在发现新冠病毒感染者后要求各区必须每天及时上报新增疑似
病例人数.A区上报的连续 7 天新增疑似病例数据是“总体均值为 3,中
位数 4”,B 区上报的连续 7 天新增疑似病例数据是“总体均值为 2,总体
方差为 ” 设A区和B区连续7天上报新增疑似病例人数分别为 , ,
, 和 , , , , 和 分别表示 A区和 B
区第 i 天上报新增疑似病例人数 和 均为非负 设
,
比较 M和 N 的大小;
求 M和 N 中较小的那个字母所对应的7 个数有多少组?
5
21. 已知椭圆 的左、右顶点分别为 、 ,离心率为 ,
长轴长为 4,动点 在 上且位于 轴上方,直线 , 与直线
分别交于 , 两点.
(1)求 的最小值;
(2)当 最小时,在椭圆 上可以找出点 使 的面积为 ,
试确定点 T的个数。
22. 已知函数 (其中 a≠0, )
1 当 时,求函数 的单调区间;
2 对任意的 均满足 ,试确定 a 的取值范围.
6
南京二十九中 2022 届高三摸底测试
数学参考答案及评分标准
一、单项选择题(本大题共 8 小题,每小题 5 分,共 40 分;每题只有一个
选项符合题意)
1-5:BABBB 6-8:ACC
二、多项选择题(本大题共 4 小题,每小题 5 分,共 20 分;每题全选且正
确得 5 分,部分选择且正确的得2 分,有选错的得 0 分)
9.AD 10.ABD 11.AD 12.ABC
三、填空题(本大题共 4 小题,每小题 5 分,共 20 分)
13. 14.
15. 4 16. ,
四、解答题(本大题共 6 小题,第 17 题满分 10 分,其余每题满分 12 分,
共 70 分)
17.解: 中,由正弦定理可得 ,
所以 可转化为 ,
又因为 ,所以 ,
所以 ,
整理得 ,
在 中 ,则 ,
又因为 ,
所以 ;
由正弦定理得 ,
则
,
又 ,所以 ,
又 ,得 ,
由余弦定理得 ,所以 ,
所以 ;
(2)因为 ,
所以 ,
所以 ,
7
又 , ,
所以 ,
由正弦定理 ,所以 , ,
代入化简得 ,所以 .
18.解: 1 设等差数列 的公差为d,等比数列 的公比为q.
由 , ,可得 .从而 的通项公式为 .
由 ,又 ,可得 ,解得 ,从而 的通
项公式为 .
2 当n为奇数时, ,
当n为偶数时, ,
对任意的正整数n,有 ,
和
由 得
由 得 ,
由于 ,
从而得: .
8
因此, .
所以,数列 的前2n项和为 .
19. 证明: 平面 平面ABP, ,
平面 平面 , 平面ABC, 平面ABP,
又 平面ABP, ,
为直径, ,又 , ,
平面ACP,又 平面BCP, 平面 平面ACP.
解:过点Q作 交AP于D,
由 知 平面ABP, ,
因为 , , ,
所以 平面APC.
, , ,
因为 为定值.
所以三棱锥 的体积为 ,
当三棱锥 的体积最大时,Q为 的中点.
, ,且 .
,则 , ,
.
在 中, ,
,
,
,
.
设点A到平面PCQ的距离为d,则由 ,得 ,
即 ,解得 . 点A到平面PCQ的距离为 .
9
20.解: 记事件 “丙受甲感染”,事件 “丁受甲感染”,则 ,
X的取值为1,2,3
所以x的分布列为
X 1 2 3
P
对于B区,由 知,
2, , ,因为 是非负整数,所以 ,即 ,
所以 ,当 , ,中有一个取 有一个取2,其余取1时, ,
对于A区,当 , , 时,满足“总体均值为3,
中位数为4“此时 ,所以
当 时,y. , 只有两种情况:
有一个是6,有五个是1,有一个是
有一个是6,有一个是0,有两个是1,其余是2.
对于 共有 组,
对于 共有 组,故共有462组
21.解: 1
10
2
11
22.解: 当 时, , ,
,
函数 的单调递减区间为 ,单调递增区间为 .
由 ,得 ,
当 时, ,等价于 ,
令 ,则 ,
设 , ,
则 ,
当 时, ,
则 ,
记 , ,
则
,
列表讨论:
x 1
0
极小值
,
.
当 时, ,
令 , ,
则 ,
故 在 上单调递增, ,
由 得 ,
12
, ,
由 知对任意 , , ,
即对任意 ,均有 ,
综上所述,所求的a的取值范围是
13
数 学 试 题
注意事项:
1.本卷共6页,包括22小题,满分150分,考试时间120分钟。答卷前,考生务
必将自己的姓名、准考证号等填写在答题卡的指定位置上并准确粘贴条形码。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂
黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在
答题卡上。写在本试卷上无效。
3.考试结束后,将答题卡交回。
一、单项选择题(本大题共 8 小题,每小题 5 分,共 40 分;每题只有一个
选项符合题意)
1. 集合 ,则(CRM)∩N=
A. B. C. D.
2. 是 的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分又不必要条件
3. 如图,放置的边长为 1 的正方形 PABC 沿 x轴滚动,点 B 恰好经过原点,
设顶点 的轨迹方程是 ,则对函数 有下列命题:
若 ,则函数 是偶函数; 对任意的 ,都有
; 函数 在区间 上单调递减; 函数
在区间 上是减函数.其中真命题的序号是
A. B. C. D.
4. 声强级 单位: 与声强I的函数关系式为: 若普通列
车的声强级是 95dB,高速列车的声强级为 45dB,则普通列车的声强是
高速列车声强的
A. 倍 B. 倍 C. 倍 D. 倍
5. 某艺术爱好者对 蒙娜丽莎 的同比例影像作品进行了测绘。将画中女
子的嘴唇近似看作一个圆弧,在嘴角A,C 处作圆弧的切线,两条切线
交于 B点,测得如下数据: , , 根
据测量得到的结果推算女子的嘴唇视作的圆弧对应的圆心角位于
1
A. B. C. D.
6. 圭表 如图 是我国古代一种通过测量正午日影长度来推定节气的天文
仪器,它包括一根直立的标竿 称为“表” 和一把呈南北方向水平固定摆
放的与标竿垂直的长尺 称为“圭” 当正午太阳照射在表上时,日影便会
投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短
的那一天定为夏至.图 2 是一个根据南京市的地理位置设计的圭表的示
意图,已知南京市冬至正午太阳高度角 即 约为 ,夏至正午
太阳高度角 即 约为 ,圭面上冬至线与夏至线之间的距离
即 DB 的长 为 a,则表高 即 AC 的长 为
A. B.
C. D.
7. 已知 , ,且 ,则向量 在向量
方向上的投影的最大值为
A. 4 B. 2 C. 1 D.
8. 已知四面体 ,分别在棱 , , 上取 等分
点,形成点列 , , ,过 , , 作四面
体的截面,记该截面的面积为 ,则
A. 数列 为等差数列 B. 数列 为等比数列
C. 数列 为等差数列 D. 数列 为等比数列
2
二、多项选择题(本大题共 4 小题,每小题 5 分,共 20 分;每题全选且正
确得 5 分,部分选择且正确的得2 分,有选错的得 0 分)
9. 函数 ,若 在 和 处切线平行,则
A. B. C. D.
10. 分别是双曲线 的左、右焦点,A 为左顶点,P
为双曲线右支上一点,若 且 的最小内角为 ,则
A. 双曲线的离心率
B. 双曲线的渐近线方程为
C.
D. 直线 与双曲线有两个公共点
11. 甲罐中有 3 个红球、2 个白球,乙罐中有 4 个红球、1 个白球,先从甲罐
中随机取出 1 个球放入乙罐,分别以 , 表示由甲罐中取出的球是红
球、白球的事件,再从乙罐中随机取出1 个球,以 B表示从乙罐中取出
的球是红球的事件,下列判断正确的是
A. B. 事件 B 与事件 相互独立
C. 事件 B 与事件 相互独立 D. , 互斥
12. 如图,在矩形 ABCD中, ,E 为 AB 的中点,将 沿
DE 翻折到 的位置, 平面 ABCD,M为 的中点,则在翻折
过程中,下列结论正确的是
A. 平面
B. B 与 M两点间距离为定值
C. 三棱锥 的体积的最大值为
D. 存在某个位置,使得平面 平面
三、填空题(本大题共 4 小题,每小题 5 分,共 20 分)
13. 已知复数 z 满足 ,且 其中 i 是虚数单位 ,则复数
▲ .
14. 剪纸社团某学生剪出了三个互相外切的圆,其半径分别为 , ,
单位: ,则三个圆之间空隙部分的面积为 ▲ .
15. 过抛物线 C: 的准线上任意一点 P作抛物线 C 的切线 PA,PB,
切点分别为 A,B,则点 A 到准线的距离与点 B 到准线的距离之和的最小
值是 ▲ .
3
16. 已知向量 , 满足 , ,若存在不同的实数 , ,
使得 ,且 ,则 的
取值范围是 ▲ .
四、解答题(本大题共 6 小题,第 17 题满分 10 分,其余每题满分 12 分,
共 70 分)
17. 在 中,设 A、B、C 所对的边分别为 a、b、c,已知 ,
且三角形外接圆半径为 .
(1)若 的面积为 ,求 的值;
(2)设 的外接圆圆心为 O,且满足 ,
求 m的值.
18. 已知 为等差数列, 为等比数列, , ,
.
1 求 和 的通项公式;
2 对任意的正整数 n,设 ,求数列 的前
2n 项和.
4
19. 如图,等腰直角三角形 ABC 所在的平面与半圆弧 AB所在的平面垂直,
,P是弧 AB 上一点,且 .
证明:平面 平面 ACP;
若 Q是弧 AP 上异于 A,P的一个动点,且 ,当三棱锥
体积最大时,求点 A到平面 PCQ的距离.
20. 某在外务工人员甲不知自己已感染新冠病毒(处于潜伏期),他从疫区
回乡过春节,这期间他和乙、丙、丁三位朋友相聚。最终,乙、丙、丁
也感染了新冠病毒.此时,乙被肯定是受甲感染,丙是受甲或乙感染的。
假设他受甲和受乙感染的概率分别是 和 丁是受甲、乙或丙感染的,
假设他受甲、乙和丙感染的概率分别是 、 和 在这种假设之下,
乙、丙、丁中直接受甲感染的人数为X.
求 X的分布列和数学期望;
该市在发现新冠病毒感染者后要求各区必须每天及时上报新增疑似
病例人数.A区上报的连续 7 天新增疑似病例数据是“总体均值为 3,中
位数 4”,B 区上报的连续 7 天新增疑似病例数据是“总体均值为 2,总体
方差为 ” 设A区和B区连续7天上报新增疑似病例人数分别为 , ,
, 和 , , , , 和 分别表示 A区和 B
区第 i 天上报新增疑似病例人数 和 均为非负 设
,
比较 M和 N 的大小;
求 M和 N 中较小的那个字母所对应的7 个数有多少组?
5
21. 已知椭圆 的左、右顶点分别为 、 ,离心率为 ,
长轴长为 4,动点 在 上且位于 轴上方,直线 , 与直线
分别交于 , 两点.
(1)求 的最小值;
(2)当 最小时,在椭圆 上可以找出点 使 的面积为 ,
试确定点 T的个数。
22. 已知函数 (其中 a≠0, )
1 当 时,求函数 的单调区间;
2 对任意的 均满足 ,试确定 a 的取值范围.
6
南京二十九中 2022 届高三摸底测试
数学参考答案及评分标准
一、单项选择题(本大题共 8 小题,每小题 5 分,共 40 分;每题只有一个
选项符合题意)
1-5:BABBB 6-8:ACC
二、多项选择题(本大题共 4 小题,每小题 5 分,共 20 分;每题全选且正
确得 5 分,部分选择且正确的得2 分,有选错的得 0 分)
9.AD 10.ABD 11.AD 12.ABC
三、填空题(本大题共 4 小题,每小题 5 分,共 20 分)
13. 14.
15. 4 16. ,
四、解答题(本大题共 6 小题,第 17 题满分 10 分,其余每题满分 12 分,
共 70 分)
17.解: 中,由正弦定理可得 ,
所以 可转化为 ,
又因为 ,所以 ,
所以 ,
整理得 ,
在 中 ,则 ,
又因为 ,
所以 ;
由正弦定理得 ,
则
,
又 ,所以 ,
又 ,得 ,
由余弦定理得 ,所以 ,
所以 ;
(2)因为 ,
所以 ,
所以 ,
7
又 , ,
所以 ,
由正弦定理 ,所以 , ,
代入化简得 ,所以 .
18.解: 1 设等差数列 的公差为d,等比数列 的公比为q.
由 , ,可得 .从而 的通项公式为 .
由 ,又 ,可得 ,解得 ,从而 的通
项公式为 .
2 当n为奇数时, ,
当n为偶数时, ,
对任意的正整数n,有 ,
和
由 得
由 得 ,
由于 ,
从而得: .
8
因此, .
所以,数列 的前2n项和为 .
19. 证明: 平面 平面ABP, ,
平面 平面 , 平面ABC, 平面ABP,
又 平面ABP, ,
为直径, ,又 , ,
平面ACP,又 平面BCP, 平面 平面ACP.
解:过点Q作 交AP于D,
由 知 平面ABP, ,
因为 , , ,
所以 平面APC.
, , ,
因为 为定值.
所以三棱锥 的体积为 ,
当三棱锥 的体积最大时,Q为 的中点.
, ,且 .
,则 , ,
.
在 中, ,
,
,
,
.
设点A到平面PCQ的距离为d,则由 ,得 ,
即 ,解得 . 点A到平面PCQ的距离为 .
9
20.解: 记事件 “丙受甲感染”,事件 “丁受甲感染”,则 ,
X的取值为1,2,3
所以x的分布列为
X 1 2 3
P
对于B区,由 知,
2, , ,因为 是非负整数,所以 ,即 ,
所以 ,当 , ,中有一个取 有一个取2,其余取1时, ,
对于A区,当 , , 时,满足“总体均值为3,
中位数为4“此时 ,所以
当 时,y. , 只有两种情况:
有一个是6,有五个是1,有一个是
有一个是6,有一个是0,有两个是1,其余是2.
对于 共有 组,
对于 共有 组,故共有462组
21.解: 1
10
2
11
22.解: 当 时, , ,
,
函数 的单调递减区间为 ,单调递增区间为 .
由 ,得 ,
当 时, ,等价于 ,
令 ,则 ,
设 , ,
则 ,
当 时, ,
则 ,
记 , ,
则
,
列表讨论:
x 1
0
极小值
,
.
当 时, ,
令 , ,
则 ,
故 在 上单调递增, ,
由 得 ,
12
, ,
由 知对任意 , , ,
即对任意 ,均有 ,
综上所述,所求的a的取值范围是
13
同课章节目录
