2021-2022学年人教版数学八年级上册 11.3多边形及内角和 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册 11.3多边形及内角和 同步练习(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 93.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 00:00:00 | ||
图片预览



文档简介
11.3多边形及内角和
一.选择题
1.正九边形的内角和为( )
A.180° B.360° C.720° D.1260°
2.正六边形的外角和为( )
A.180° B.360° C.540° D.720°
3.正多边形的一个外角等于60°,这个多边形的边数是( )
A.3 B.6 C.9 D.12
4.如果一个正多边形的一个内角与一个外角的度数之比是7:2,那么这个正多边形的边数是( )
A.11 B.10 C.9 D.8
5.正八边形中,每个内角与每个外角的度数之比为( )
A.1:3 B.1:2 C.2:1 D.3:1
6.一个十边形的内角和等于( )
A.1800° B.1660° C.1440° D.1200°
7.如图,点A、B、C、D、E在同一平面内连接AB、BC、CD、DE、EA,若∠BCD=100°,则∠A+∠B+∠D+∠E=( )
A.220° B.240° C.260° D.280°
8.如果一个多边形的内角和等于它的外角和的2倍,那么这个多边形的边数是( )
A.4 B.5 C.6 D.8
9.如果剪掉四边形的一个角,那么所得多边形的内角和的度数不可能是( )
A.180° B.270° C.360° D.540°
10.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )
A.10或11 B.11或12或13 C.11或12 D.10或11或12
二.填空题
11.如果多边形的每个内角都等于150°,则它的边数为 .
12.如果一个多边形的每个外角都是60°,那么这个多边形内角和的度数为 .
13.若一个正多边形的每一个外角都等于相邻内角的,则这个多边形的内角和为 度.
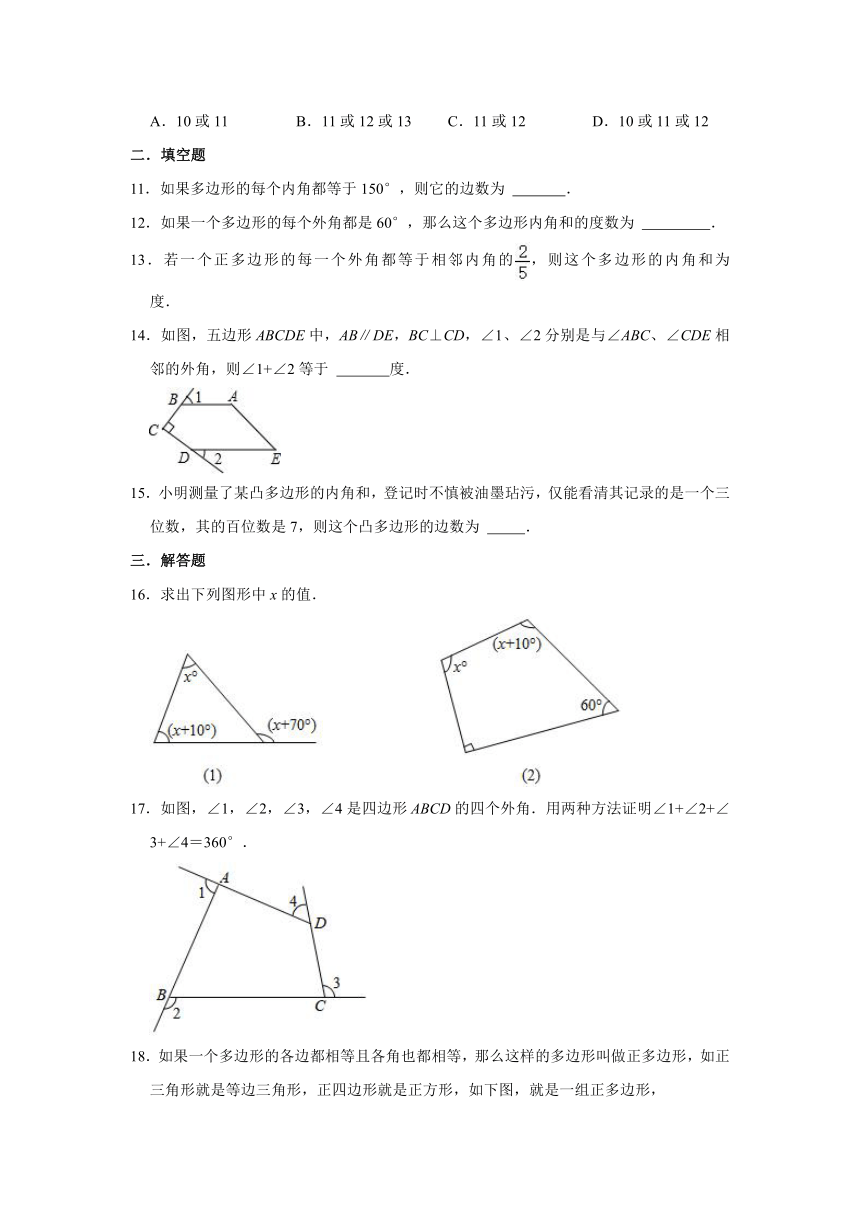
14.如图,五边形ABCDE中,AB∥DE,BC⊥CD,∠1、∠2分别是与∠ABC、∠CDE相邻的外角,则∠1+∠2等于 度.
15.小明测量了某凸多边形的内角和,登记时不慎被油墨玷污,仅能看清其记录的是一个三位数,其的百位数是7,则这个凸多边形的边数为 .
三.解答题
16.求出下列图形中x的值.
17.如图,∠1,∠2,∠3,∠4是四边形ABCD的四个外角.用两种方法证明∠1+∠2+∠3+∠4=360°.
18.如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,
(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 3 4 5 6 … n
∠α的度数 …
(2)根据规律,计算正八边形中的∠α的度数;
(3)是否存在正n边形使得∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
参考答案
一.选择题
1.解:由题意得:
正九边形的内角和为(9﹣2)×180°=1260°,
故选:D.
2.解:正六边形的外角和是360°.
故选:B.
3.解:∵正多边形的外角和为360°,
∴此多边形的边数为:360°÷60°=6.
故选:B.
4.解:设这个正多边形的边数为n,
由题意得:(n﹣2)×180=360,
解得:n=9,
故选:C.
5.解:这个八边形的内角和为:
(8﹣2)×180°=1080°;
这个八边形的每个内角的度数为:
1080°÷8=135°;
这个八边形的每个外角的度数为:
360°÷8=45°;
∴这个八边形每个内角与每个外角的度数之比为:
135:45=3:1.
故选:D.
6.解:根据多边形内角和公式得,十边形的内角和等于:
(10﹣2)×180°=8×180°=1440°,
故选:C.
7.解:连接BD,
∵∠BCD=100°,
∴∠CBD+∠CDB=180°﹣100°=80°,
∴∠A+∠ABC+∠E+∠CDE=360°﹣∠CBD﹣∠CDB=360°﹣80°=280°,
故选:D.
8.解:根据题意,得:
(n﹣2)?180°=720°,
解得:n=6.
故选:C.
9.解:剪去一个角,若边数减少1,则内角和=(3﹣2)?180°=180°,
若边数不变,则内角和=(4﹣2)?180°=360°,
若边数增加1,则内角和=(5﹣2)?180°=540°,
所以,所得多边形内角和的度数可能是180°,360°,540°,不可能是270°.
故选:B.
10.解:设多边形截去一个角的边数为n,
则(n﹣2)?180°=1620°,
解得n=11,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是10或11或12.
故选:D.
二.填空题
11.解:∵多边形的每个内角都等于150°,
∴多边形的每个外角为180°﹣150°=30°,
∴多边形的边数为360÷30=12.
故答案为12.
12.解:∵一个多边形的每个外角都是60°,
∴n=360°÷60°=6,
则内角和为:(6﹣2)?180°=720°,
故答案为:720°.
13.解:设正多边形的外角是x,则相邻的内角是x,
根据题意得:x+x=180°,
解得x=.
则正多边形的边数是:360°÷=7,
则这个多边形的内角和为:(7﹣2)×180°=900°,
故答案为:900.
14.解:连接BD,
∵BC⊥CD,
∴∠C=90°,
∴∠CBD+∠CDB=180°﹣90°=90°,
∵AB∥DE,
∴∠ABD+∠EDB=180°,
∴∠1+∠2=(180°﹣∠ABC)+(180°﹣∠EDC)
=360°﹣(∠ABC+∠EDC)
=360°﹣(∠ABD+∠CBD+∠EDB+∠CDB)
=360°﹣(90°+180°)
=90°,
故答案为:90.
15.解:根据多边形的内角和公式可知,多边形的内角和是180的整数倍数,
是一个三位数,百位数是7的,又是180的整数倍数的只有720,
故多边形的内角和为720°,
这个凸多边形的边数为:+2=6,
故答案为:6.
三.解答题
16.解:(1)由三角形的外角性质得,x+(x+10)=x+70,
即2x+10=x+70,
解得,x=60.
(2)根据四边形的内角和为360°得,
x+(x+10)+90+60=360,
解得,x=100.
17.证法1:
∵∠1+∠BAD=180°,∠2+∠ABC=180°,∠3+∠BCD=180°,∠4+∠CDA=180°,
∴∠1+∠BAD+∠2+∠ABC+∠3+∠BCD+∠4+∠CDA=180°×4=720°.
∵∠BAD+∠ABC+∠BCD+∠CDA=360°,
∴∠1+∠2+∠3+∠4=360°.
证法2:连接BD,
∵∠1=∠ABD+∠ADB,∠3=∠CBD+∠CDB,
∴∠1+∠2+∠3+∠4=∠ABD+∠ADB+∠2+∠CBD+∠CDB+∠4=180°×2=360°.
18.解:(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 3 4 5 6 … n
∠α的度数 60° 45° 36° 30° … ()°
(2)根据规律,计算正八边形中的∠α=()°=22.5°;
(3)不存在,理由如下:
设存在正n边形使得∠α=21°,
得∠α=21°=()°.
解得n=8,n是正整数,n=8(不符合题意要舍去),
不存在正n边形使得∠α=21°.
一.选择题
1.正九边形的内角和为( )
A.180° B.360° C.720° D.1260°
2.正六边形的外角和为( )
A.180° B.360° C.540° D.720°
3.正多边形的一个外角等于60°,这个多边形的边数是( )
A.3 B.6 C.9 D.12
4.如果一个正多边形的一个内角与一个外角的度数之比是7:2,那么这个正多边形的边数是( )
A.11 B.10 C.9 D.8
5.正八边形中,每个内角与每个外角的度数之比为( )
A.1:3 B.1:2 C.2:1 D.3:1
6.一个十边形的内角和等于( )
A.1800° B.1660° C.1440° D.1200°
7.如图,点A、B、C、D、E在同一平面内连接AB、BC、CD、DE、EA,若∠BCD=100°,则∠A+∠B+∠D+∠E=( )
A.220° B.240° C.260° D.280°
8.如果一个多边形的内角和等于它的外角和的2倍,那么这个多边形的边数是( )
A.4 B.5 C.6 D.8
9.如果剪掉四边形的一个角,那么所得多边形的内角和的度数不可能是( )
A.180° B.270° C.360° D.540°
10.一个多边形截去一个角后,形成的另一个多边形的内角和是1620°,则原来多边形的边数是( )
A.10或11 B.11或12或13 C.11或12 D.10或11或12
二.填空题
11.如果多边形的每个内角都等于150°,则它的边数为 .
12.如果一个多边形的每个外角都是60°,那么这个多边形内角和的度数为 .
13.若一个正多边形的每一个外角都等于相邻内角的,则这个多边形的内角和为 度.
14.如图,五边形ABCDE中,AB∥DE,BC⊥CD,∠1、∠2分别是与∠ABC、∠CDE相邻的外角,则∠1+∠2等于 度.
15.小明测量了某凸多边形的内角和,登记时不慎被油墨玷污,仅能看清其记录的是一个三位数,其的百位数是7,则这个凸多边形的边数为 .
三.解答题
16.求出下列图形中x的值.
17.如图,∠1,∠2,∠3,∠4是四边形ABCD的四个外角.用两种方法证明∠1+∠2+∠3+∠4=360°.
18.如果一个多边形的各边都相等且各角也都相等,那么这样的多边形叫做正多边形,如正三角形就是等边三角形,正四边形就是正方形,如下图,就是一组正多边形,
(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 3 4 5 6 … n
∠α的度数 …
(2)根据规律,计算正八边形中的∠α的度数;
(3)是否存在正n边形使得∠α=21°?若存在,请求出n的值,若不存在,请说明理由.
参考答案
一.选择题
1.解:由题意得:
正九边形的内角和为(9﹣2)×180°=1260°,
故选:D.
2.解:正六边形的外角和是360°.
故选:B.
3.解:∵正多边形的外角和为360°,
∴此多边形的边数为:360°÷60°=6.
故选:B.
4.解:设这个正多边形的边数为n,
由题意得:(n﹣2)×180=360,
解得:n=9,
故选:C.
5.解:这个八边形的内角和为:
(8﹣2)×180°=1080°;
这个八边形的每个内角的度数为:
1080°÷8=135°;
这个八边形的每个外角的度数为:
360°÷8=45°;
∴这个八边形每个内角与每个外角的度数之比为:
135:45=3:1.
故选:D.
6.解:根据多边形内角和公式得,十边形的内角和等于:
(10﹣2)×180°=8×180°=1440°,
故选:C.
7.解:连接BD,
∵∠BCD=100°,
∴∠CBD+∠CDB=180°﹣100°=80°,
∴∠A+∠ABC+∠E+∠CDE=360°﹣∠CBD﹣∠CDB=360°﹣80°=280°,
故选:D.
8.解:根据题意,得:
(n﹣2)?180°=720°,
解得:n=6.
故选:C.
9.解:剪去一个角,若边数减少1,则内角和=(3﹣2)?180°=180°,
若边数不变,则内角和=(4﹣2)?180°=360°,
若边数增加1,则内角和=(5﹣2)?180°=540°,
所以,所得多边形内角和的度数可能是180°,360°,540°,不可能是270°.
故选:B.
10.解:设多边形截去一个角的边数为n,
则(n﹣2)?180°=1620°,
解得n=11,
∵截去一个角后边上可以增加1,不变,减少1,
∴原来多边形的边数是10或11或12.
故选:D.
二.填空题
11.解:∵多边形的每个内角都等于150°,
∴多边形的每个外角为180°﹣150°=30°,
∴多边形的边数为360÷30=12.
故答案为12.
12.解:∵一个多边形的每个外角都是60°,
∴n=360°÷60°=6,
则内角和为:(6﹣2)?180°=720°,
故答案为:720°.
13.解:设正多边形的外角是x,则相邻的内角是x,
根据题意得:x+x=180°,
解得x=.
则正多边形的边数是:360°÷=7,
则这个多边形的内角和为:(7﹣2)×180°=900°,
故答案为:900.
14.解:连接BD,
∵BC⊥CD,
∴∠C=90°,
∴∠CBD+∠CDB=180°﹣90°=90°,
∵AB∥DE,
∴∠ABD+∠EDB=180°,
∴∠1+∠2=(180°﹣∠ABC)+(180°﹣∠EDC)
=360°﹣(∠ABC+∠EDC)
=360°﹣(∠ABD+∠CBD+∠EDB+∠CDB)
=360°﹣(90°+180°)
=90°,
故答案为:90.
15.解:根据多边形的内角和公式可知,多边形的内角和是180的整数倍数,
是一个三位数,百位数是7的,又是180的整数倍数的只有720,
故多边形的内角和为720°,
这个凸多边形的边数为:+2=6,
故答案为:6.
三.解答题
16.解:(1)由三角形的外角性质得,x+(x+10)=x+70,
即2x+10=x+70,
解得,x=60.
(2)根据四边形的内角和为360°得,
x+(x+10)+90+60=360,
解得,x=100.
17.证法1:
∵∠1+∠BAD=180°,∠2+∠ABC=180°,∠3+∠BCD=180°,∠4+∠CDA=180°,
∴∠1+∠BAD+∠2+∠ABC+∠3+∠BCD+∠4+∠CDA=180°×4=720°.
∵∠BAD+∠ABC+∠BCD+∠CDA=360°,
∴∠1+∠2+∠3+∠4=360°.
证法2:连接BD,
∵∠1=∠ABD+∠ADB,∠3=∠CBD+∠CDB,
∴∠1+∠2+∠3+∠4=∠ABD+∠ADB+∠2+∠CBD+∠CDB+∠4=180°×2=360°.
18.解:(1)观察上面每个正多边形中的∠α,填写下表:
正多边形边数 3 4 5 6 … n
∠α的度数 60° 45° 36° 30° … ()°
(2)根据规律,计算正八边形中的∠α=()°=22.5°;
(3)不存在,理由如下:
设存在正n边形使得∠α=21°,
得∠α=21°=()°.
解得n=8,n是正整数,n=8(不符合题意要舍去),
不存在正n边形使得∠α=21°.
