12.1全等三角形 同步练习 2021-2022学年八年级数学人教版上册(word版含答案)
文档属性
| 名称 | 12.1全等三角形 同步练习 2021-2022学年八年级数学人教版上册(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 299.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 14:38:08 | ||
图片预览



文档简介
121920001130300012.1全等三角形
一、单选题
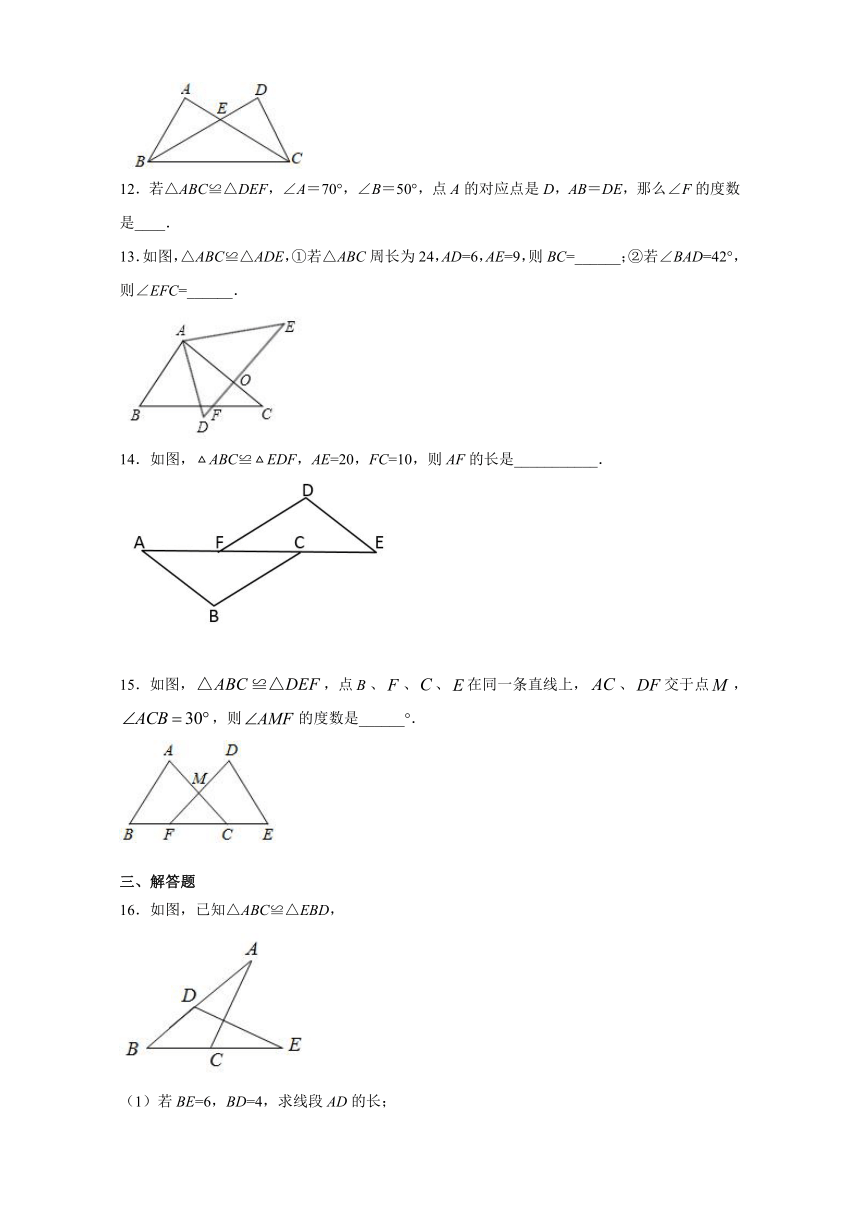
1.下列各组图形属于全等图形的是( )
A. B. C. D.
2.给出下面四个命题中,其中真命题的个数是( )
(1)全等三角形的对应边相等
(2)所有的等边三角形都全等
(3)同旁内角互补
(4)所有定理的逆命题都是真命题
A.1个 B.2个 C.3个 D.4个
3.如图,已知两个三角形全等,那么false的度数是( )
A.false B.false C.false D.false
4.如图,false,其中false,false,则false( )
A.60° B.100° C.120° D.135°
5.如图,△ABE≌△ACD,BC=10,DE=4,则DC的长是( )
A.8 B.7 C.6 D.5
6.如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )
A.∠A+∠ABD=∠C+∠CBD B.△ABD和△CDB的周长相等
C.△ABD和△CDB的面积相等 D.AD∥BC,且AD=BC
7.如图,false,false和false,false和false是对应点,false、false、false在同一直线上,且false,false,则false的长为( )
A.12 B.7 C.2 D.14
8.下列命题中不正确的是( )
A.全等三角形的对应高相等 B.全等三角形的面积相等
C.全等三角形的周长相等 D.周长相等的两个三角形全等
9.如图,点B,E,C,F在一条直线上,false,则下列结论正确的是( )
A.false B.false C.false D.false
10.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到false的位置,false,false,平移距离为6,则阴影部分面积为( )
A.48 B.42 C.40 D.24
二、填空题
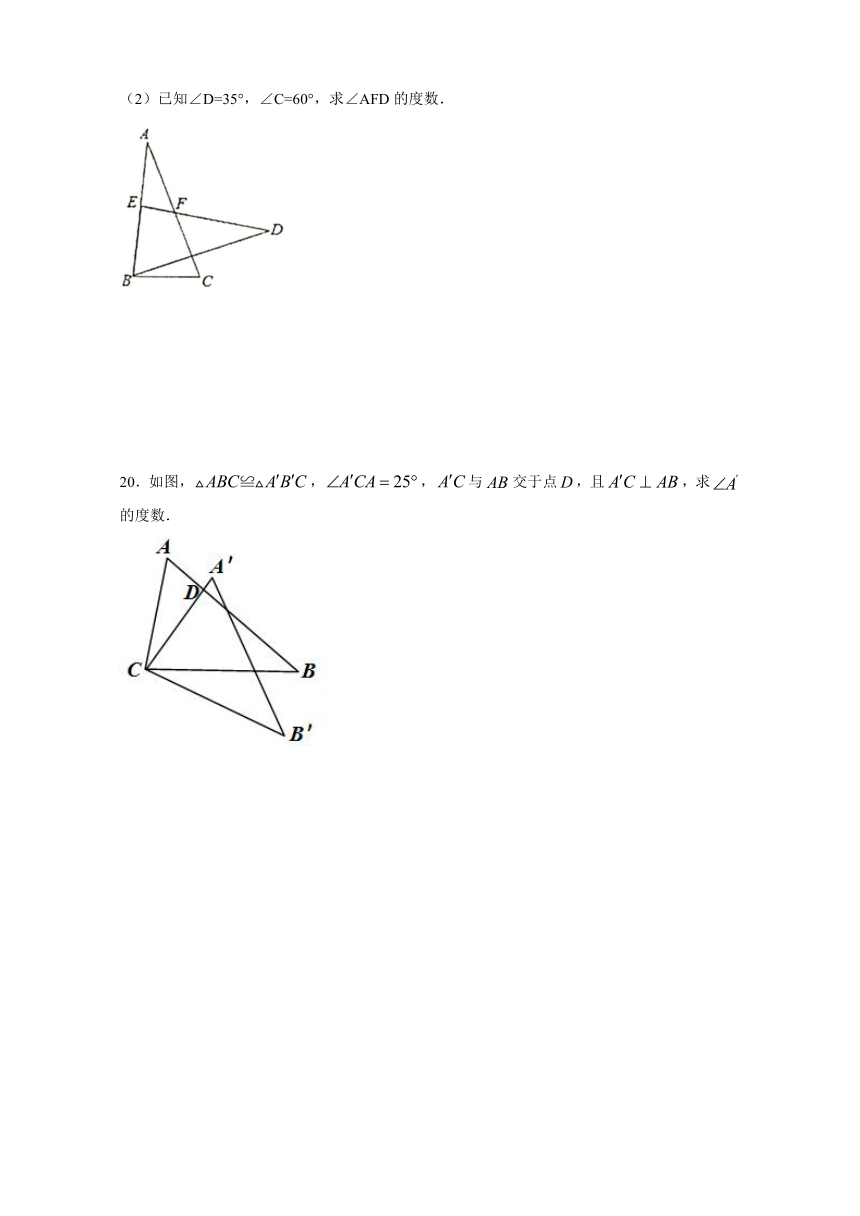
11.如图,false与false相交于点E,若false,则false等于___________.
12.若△ABC≌△DEF,∠A=70°,∠B=50°,点A的对应点是D,AB=DE,那么∠F的度数是____.
13.如图,△ABC≌△ADE,①若△ABC周长为24,AD=6,AE=9,则BC=______;②若∠BAD=42°,则∠EFC=______.
14.如图,falseABC≌falseEDF,AE=20,FC=10,则AF的长是___________.
15.如图,false,点false、false、false、false在同一条直线上,false、false交于点false,false,则false的度数是______°.
三、解答题
16.如图,已知△ABC≌△EBD,
(1)若BE=6,BD=4,求线段AD的长;
(2)若∠E=30°,∠B=48°,求∠ACE的度数.
17.如图,已知false,点false、false在线段false上.
(1)线段false与false的数量关系是:_________,判断该关系的数学根据是: (用文字表达);
(2)判断false与false之间的位置关系,并说明理由.
18.如图所示,A,D,E三点在同一直线上,且false,求证:false.
19.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=9,BC=5时,线段 AE的长为 ,
(2)已知∠D=35°,∠C=60°,求∠AFD的度数.
20.如图,false,false,false与false交于点false,且false,求false的度数.
参考答案
1.D
解:A、两个图形不属于全等图形,故此选项不合题意;
B、两个图形不属于全等图形,故此选项不合题意;
C、两个图形不属于全等图形,故此选项不合题意;
D、两个图形属于全等图形,故此选项符合题意;
故选:D.
2.A
解: ①全等三角形的对应边相等,故是真命题;
②因为所有的等边三角形的每个角都是60°,所以所有的等边三角形都相似,但不全等,故是假命题;
③因为前提条件是:两直线平行,同旁内角互补,故不是真命题;
④因为并不是所有定理的逆命题都是真命题.例如:两个全等三角形的对应角相等,逆命题
是:三个角对应相等的两个三角形全等是假命题,故不是真命题.
所以真命题的个数有1个.
故选 A.
3.A
解:∵两个三角形全等,
∴∠2=∠1=180°-58°-72°=50°,
故选:A.
4.C
解:∵false,
∴false,
∵false,
∴false;
故选:C.
5.B
解:∵△ABE≌△ACD,
∴BE=CD,
∴BE+CD=BC+DE=14,
∴2CD=14,
∴CD=7,
故选:B.
6.A
解:∵△ABD≌△CDB,AB,CD是对应边,
∴∠ADB=∠CBD,AD=BC,△ABD和△CDB的面积相等,△ABD和△CDB的周长相等,
∴AD∥BC,
则选项B,C,D一定正确.
由△ABD≌△CDB不一定能得到∠ABD=∠CBD,因而∠A+∠ABD=∠C+∠CBD不一定成立,
故选:A.
7.A
解:如图,false,false和false,false和false是对应点,false、false、false在同一直线上,且false,false,
false,false,
false.
故选:false.
8.D
解:如图所示,∵△ABC≌△EFG,
∴AC=EG,∠A=∠E,
∵∠ADC=∠EHG=90°,
∴△ADC≌△EHG,
∴DC=HG,
∴全等三角形的对应高相等,正确,
∴选项A不符合题意;
∵△ABC≌△EFG,
∴AC=EG,AB=EF,BC=FG,
∴AB+BC+CA=EF+FG+GH,
∴全等三角形的周长相等,正确,
∴选项C不符合题意;
根据前面的证明,得AB=EF,DC=HG,
∴false,
∴全等三角形的面积相等,正确,
∴选项B不符合题意;
如等腰三角形的腰长为5,底边为2,周长为12,等边三角形的边长为4,周长为12,但两个三角形不会全等,
∴选项D符合题意;
故选D.
9.D
解:∵△ABC≌△DFE,
∴∠ABC=∠DFE,AB=DF,∠ACB=∠GEC,
故A、B、C选项均不正确,不符合题意;
∵∠ACB=∠GEC,
∴GE=GC,
∵△ABC≌△DFE,
∴AC=DE,
∴AC-GC=DE-GE,
∴AG=DG,故D选项符合题意.
故选:D.
10.A
解:由平移的性质知,BE=6,DE=AB=10,
∴OE=DE-DO=10-4=6,
∵△ABC≌△DEF,
∴S△ABC=S△DEF,
∴S四边形ODFC=S梯形ABEO=false(AB+OE)?BE=false(10+6)×6=48,
故选:A.
11.false
解:∵△ABC≌△DCB,∠ACB=40°,
∴∠DBC=∠ACB=40°,
∴∠BEC=180°-∠DBC-∠ACB=180°-40°-40°=100°,
故答案为:100°.
12.60°
解:∵△ABC≌△DEF,∠A=70°,∠B=50°,
∴∠F=∠C=180°﹣∠A﹣∠B=60°.
故答案为:60°.
13.9 42°
解:①∵△ABC≌△ADE,
∴AB=AD=6,AC=AE=9,
∵△ABC周长为24,
∴BC=24-6-9=9;
②∵△ABC≌△ADE,
∴∠BAC=∠DAE,∠C=∠E,
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠CAE=∠BAD=42°,
∴∠EFC=∠CAE=42°.
故答案为:9;42°.
14.5
解:∵falseABC≌falseEDF,
∴AC=EF,
∴AC-FC=EF-FC,
∴AF=EC,
∴AF=false.
故答案为:5
15.60
解:∵△ABC≌△DEF,
∴∠DFE=∠ACB=30°,
∵∠AMF是△MFC的一个外角,
∴∠AMF=∠DFE+∠ACB=60°,
故答案为:60.
16.(1)2;(2)78°.
解:(1)∵△ABC≌△EBD,
∴AB=BE=6,
∵AD=AB-BD,BD=4,
∴AD=6-4=2;
(2)∵△ABC≌△EBD,
∴∠A=∠E=30°,
∵∠ACE=∠A+∠B,∠B=48°,
∴∠ACE=30°+48°
=78°.
17.(1)相等(或写false),全等三角形的对应边相等;(2)false,见详解
解:(1)∵false
∴AD=BC
根据全等三角形的对应边相等
故答案为:相等(或写false)
全等三角形的对应边相等
(2)猜想:false.
理由:
∵false,
∴false,
∵∠ADB=180°-∠ADF
∠CBD=180°-∠CBE
∴false,
∴false
故答案为false
18.证明见解析.
证明:false,
false,false,
false,
false.
19.(1)false;(2)130°.
解:(1)false △ABC≌△DEB,DE=9,BC=5,
false
false
故答案为:false
(2)false △ABC≌△DEB,∠C=60°,∠D=35°,
false false
false ∠D=35°,
false
false
20.65°
解:false,
false,
false.
false,
false.
一、单选题
1.下列各组图形属于全等图形的是( )
A. B. C. D.
2.给出下面四个命题中,其中真命题的个数是( )
(1)全等三角形的对应边相等
(2)所有的等边三角形都全等
(3)同旁内角互补
(4)所有定理的逆命题都是真命题
A.1个 B.2个 C.3个 D.4个
3.如图,已知两个三角形全等,那么false的度数是( )
A.false B.false C.false D.false
4.如图,false,其中false,false,则false( )
A.60° B.100° C.120° D.135°
5.如图,△ABE≌△ACD,BC=10,DE=4,则DC的长是( )
A.8 B.7 C.6 D.5
6.如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )
A.∠A+∠ABD=∠C+∠CBD B.△ABD和△CDB的周长相等
C.△ABD和△CDB的面积相等 D.AD∥BC,且AD=BC
7.如图,false,false和false,false和false是对应点,false、false、false在同一直线上,且false,false,则false的长为( )
A.12 B.7 C.2 D.14
8.下列命题中不正确的是( )
A.全等三角形的对应高相等 B.全等三角形的面积相等
C.全等三角形的周长相等 D.周长相等的两个三角形全等
9.如图,点B,E,C,F在一条直线上,false,则下列结论正确的是( )
A.false B.false C.false D.false
10.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到false的位置,false,false,平移距离为6,则阴影部分面积为( )
A.48 B.42 C.40 D.24
二、填空题
11.如图,false与false相交于点E,若false,则false等于___________.
12.若△ABC≌△DEF,∠A=70°,∠B=50°,点A的对应点是D,AB=DE,那么∠F的度数是____.
13.如图,△ABC≌△ADE,①若△ABC周长为24,AD=6,AE=9,则BC=______;②若∠BAD=42°,则∠EFC=______.
14.如图,falseABC≌falseEDF,AE=20,FC=10,则AF的长是___________.
15.如图,false,点false、false、false、false在同一条直线上,false、false交于点false,false,则false的度数是______°.
三、解答题
16.如图,已知△ABC≌△EBD,
(1)若BE=6,BD=4,求线段AD的长;
(2)若∠E=30°,∠B=48°,求∠ACE的度数.
17.如图,已知false,点false、false在线段false上.
(1)线段false与false的数量关系是:_________,判断该关系的数学根据是: (用文字表达);
(2)判断false与false之间的位置关系,并说明理由.
18.如图所示,A,D,E三点在同一直线上,且false,求证:false.
19.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=9,BC=5时,线段 AE的长为 ,
(2)已知∠D=35°,∠C=60°,求∠AFD的度数.
20.如图,false,false,false与false交于点false,且false,求false的度数.
参考答案
1.D
解:A、两个图形不属于全等图形,故此选项不合题意;
B、两个图形不属于全等图形,故此选项不合题意;
C、两个图形不属于全等图形,故此选项不合题意;
D、两个图形属于全等图形,故此选项符合题意;
故选:D.
2.A
解: ①全等三角形的对应边相等,故是真命题;
②因为所有的等边三角形的每个角都是60°,所以所有的等边三角形都相似,但不全等,故是假命题;
③因为前提条件是:两直线平行,同旁内角互补,故不是真命题;
④因为并不是所有定理的逆命题都是真命题.例如:两个全等三角形的对应角相等,逆命题
是:三个角对应相等的两个三角形全等是假命题,故不是真命题.
所以真命题的个数有1个.
故选 A.
3.A
解:∵两个三角形全等,
∴∠2=∠1=180°-58°-72°=50°,
故选:A.
4.C
解:∵false,
∴false,
∵false,
∴false;
故选:C.
5.B
解:∵△ABE≌△ACD,
∴BE=CD,
∴BE+CD=BC+DE=14,
∴2CD=14,
∴CD=7,
故选:B.
6.A
解:∵△ABD≌△CDB,AB,CD是对应边,
∴∠ADB=∠CBD,AD=BC,△ABD和△CDB的面积相等,△ABD和△CDB的周长相等,
∴AD∥BC,
则选项B,C,D一定正确.
由△ABD≌△CDB不一定能得到∠ABD=∠CBD,因而∠A+∠ABD=∠C+∠CBD不一定成立,
故选:A.
7.A
解:如图,false,false和false,false和false是对应点,false、false、false在同一直线上,且false,false,
false,false,
false.
故选:false.
8.D
解:如图所示,∵△ABC≌△EFG,
∴AC=EG,∠A=∠E,
∵∠ADC=∠EHG=90°,
∴△ADC≌△EHG,
∴DC=HG,
∴全等三角形的对应高相等,正确,
∴选项A不符合题意;
∵△ABC≌△EFG,
∴AC=EG,AB=EF,BC=FG,
∴AB+BC+CA=EF+FG+GH,
∴全等三角形的周长相等,正确,
∴选项C不符合题意;
根据前面的证明,得AB=EF,DC=HG,
∴false,
∴全等三角形的面积相等,正确,
∴选项B不符合题意;
如等腰三角形的腰长为5,底边为2,周长为12,等边三角形的边长为4,周长为12,但两个三角形不会全等,
∴选项D符合题意;
故选D.
9.D
解:∵△ABC≌△DFE,
∴∠ABC=∠DFE,AB=DF,∠ACB=∠GEC,
故A、B、C选项均不正确,不符合题意;
∵∠ACB=∠GEC,
∴GE=GC,
∵△ABC≌△DFE,
∴AC=DE,
∴AC-GC=DE-GE,
∴AG=DG,故D选项符合题意.
故选:D.
10.A
解:由平移的性质知,BE=6,DE=AB=10,
∴OE=DE-DO=10-4=6,
∵△ABC≌△DEF,
∴S△ABC=S△DEF,
∴S四边形ODFC=S梯形ABEO=false(AB+OE)?BE=false(10+6)×6=48,
故选:A.
11.false
解:∵△ABC≌△DCB,∠ACB=40°,
∴∠DBC=∠ACB=40°,
∴∠BEC=180°-∠DBC-∠ACB=180°-40°-40°=100°,
故答案为:100°.
12.60°
解:∵△ABC≌△DEF,∠A=70°,∠B=50°,
∴∠F=∠C=180°﹣∠A﹣∠B=60°.
故答案为:60°.
13.9 42°
解:①∵△ABC≌△ADE,
∴AB=AD=6,AC=AE=9,
∵△ABC周长为24,
∴BC=24-6-9=9;
②∵△ABC≌△ADE,
∴∠BAC=∠DAE,∠C=∠E,
∴∠BAC-∠CAD=∠DAE-∠CAD,
即∠CAE=∠BAD=42°,
∴∠EFC=∠CAE=42°.
故答案为:9;42°.
14.5
解:∵falseABC≌falseEDF,
∴AC=EF,
∴AC-FC=EF-FC,
∴AF=EC,
∴AF=false.
故答案为:5
15.60
解:∵△ABC≌△DEF,
∴∠DFE=∠ACB=30°,
∵∠AMF是△MFC的一个外角,
∴∠AMF=∠DFE+∠ACB=60°,
故答案为:60.
16.(1)2;(2)78°.
解:(1)∵△ABC≌△EBD,
∴AB=BE=6,
∵AD=AB-BD,BD=4,
∴AD=6-4=2;
(2)∵△ABC≌△EBD,
∴∠A=∠E=30°,
∵∠ACE=∠A+∠B,∠B=48°,
∴∠ACE=30°+48°
=78°.
17.(1)相等(或写false),全等三角形的对应边相等;(2)false,见详解
解:(1)∵false
∴AD=BC
根据全等三角形的对应边相等
故答案为:相等(或写false)
全等三角形的对应边相等
(2)猜想:false.
理由:
∵false,
∴false,
∵∠ADB=180°-∠ADF
∠CBD=180°-∠CBE
∴false,
∴false
故答案为false
18.证明见解析.
证明:false,
false,false,
false,
false.
19.(1)false;(2)130°.
解:(1)false △ABC≌△DEB,DE=9,BC=5,
false
false
故答案为:false
(2)false △ABC≌△DEB,∠C=60°,∠D=35°,
false false
false ∠D=35°,
false
false
20.65°
解:false,
false,
false.
false,
false.
