12.2第3课时 利用两角一边判定三角形全等(ASA,AAS) 同步练习 2021--2022学年人教版数学八年级上册(word版含答案)
文档属性
| 名称 | 12.2第3课时 利用两角一边判定三角形全等(ASA,AAS) 同步练习 2021--2022学年人教版数学八年级上册(word版含答案) | 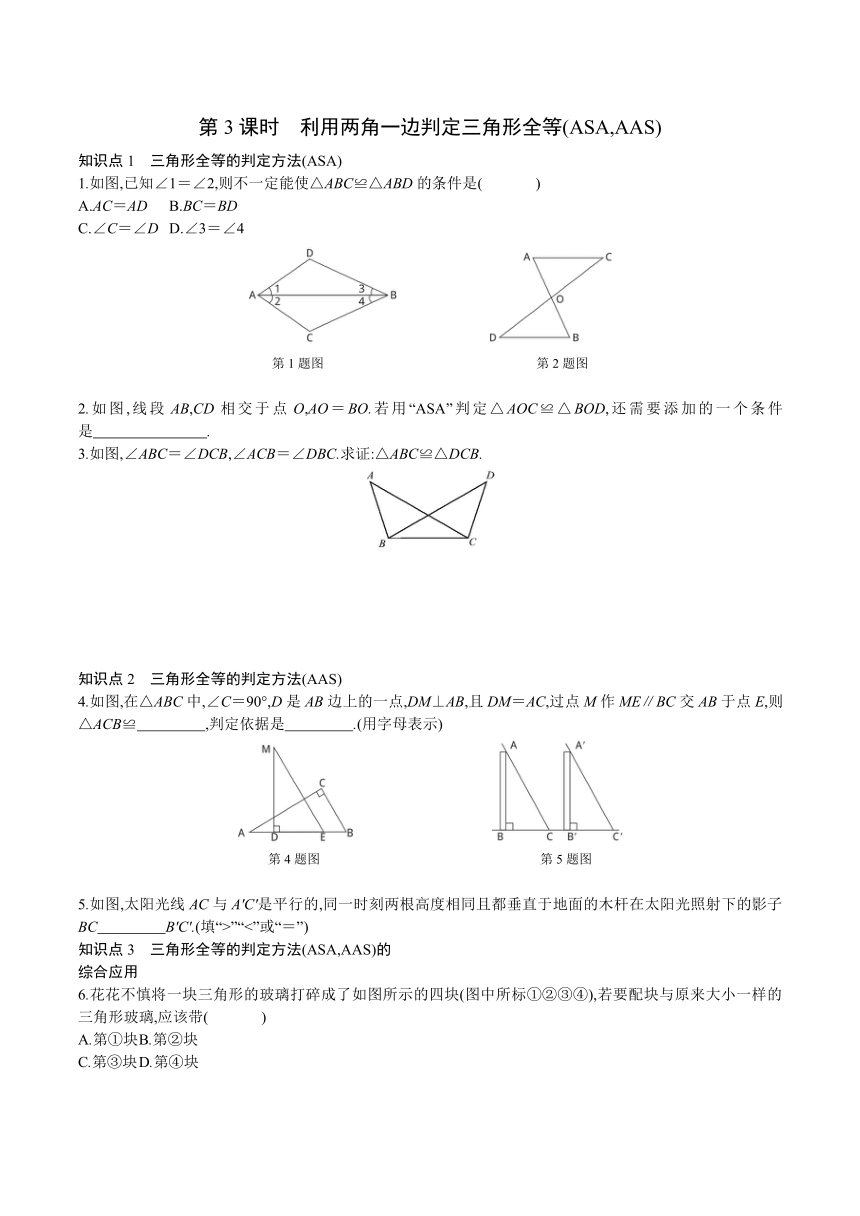 | |
| 格式 | docx | ||
| 文件大小 | 186.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 14:40:46 | ||
图片预览

文档简介
1200150011696700第3课时 利用两角一边判定三角形全等(ASA,AAS)
知识点1 三角形全等的判定方法(ASA)
1.如图,已知∠1=∠2,则不一定能使△ABC≌△ABD的条件是( )
A.AC=AD B.BC=BD
C.∠C=∠D D.∠3=∠4
第1题图 第2题图
2.如图,线段AB,CD相交于点O,AO=BO.若用“ASA”判定△AOC≌△BOD,还需要添加的一个条件是 .?
3.如图,∠ABC=∠DCB,∠ACB=∠DBC.求证:△ABC≌△DCB.
知识点2 三角形全等的判定方法(AAS)
4.如图,在△ABC中,∠C=90°,D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E,则△ACB≌ ,判定依据是 .(用字母表示)?
第4题图 第5题图
5.如图,太阳光线AC与A'C'是平行的,同一时刻两根高度相同且都垂直于地面的木杆在太阳光照射下的影子BC B'C'.(填“>”“<”或“=”)?
知识点3 三角形全等的判定方法(ASA,AAS)的
综合应用
6.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①②③④),若要配块与原来大小一样的三角形玻璃,应该带( )
A.第①块 B.第②块
C.第③块 D.第④块
第6题图 第7题图
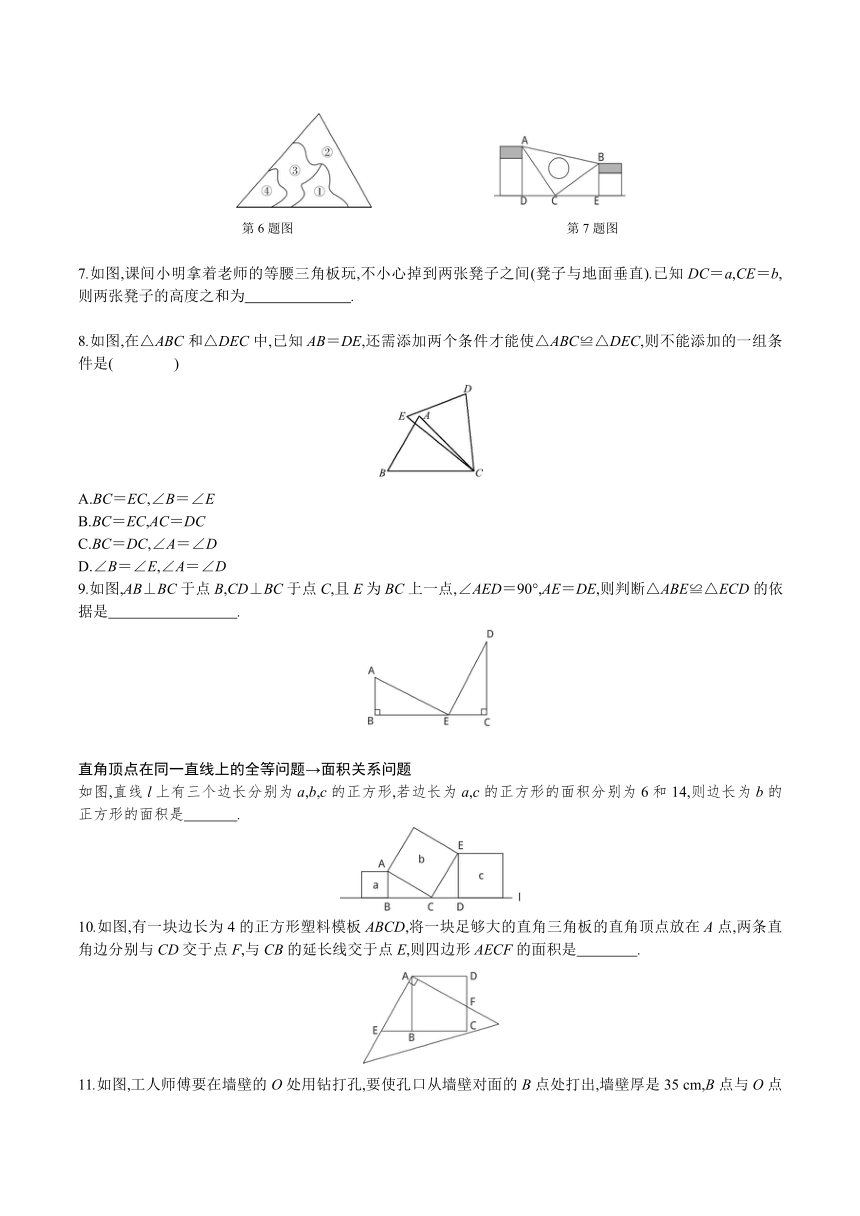
7.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两张凳子之间(凳子与地面垂直).已知DC=a,CE=b,则两张凳子的高度之和为 .?
8.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,则不能添加的一组条件是( )
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
9.如图,AB⊥BC于点B,CD⊥BC于点C,且E为BC上一点,∠AED=90°,AE=DE,则判断△ABE≌△ECD的依据是 .?
直角顶点在同一直线上的全等问题→面积关系问题
如图,直线l上有三个边长分别为a,b,c的正方形,若边长为a,c的正方形的面积分别为6和14,则边长为b的正方形的面积是 .?
10.如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点放在A点,两条直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是 .?
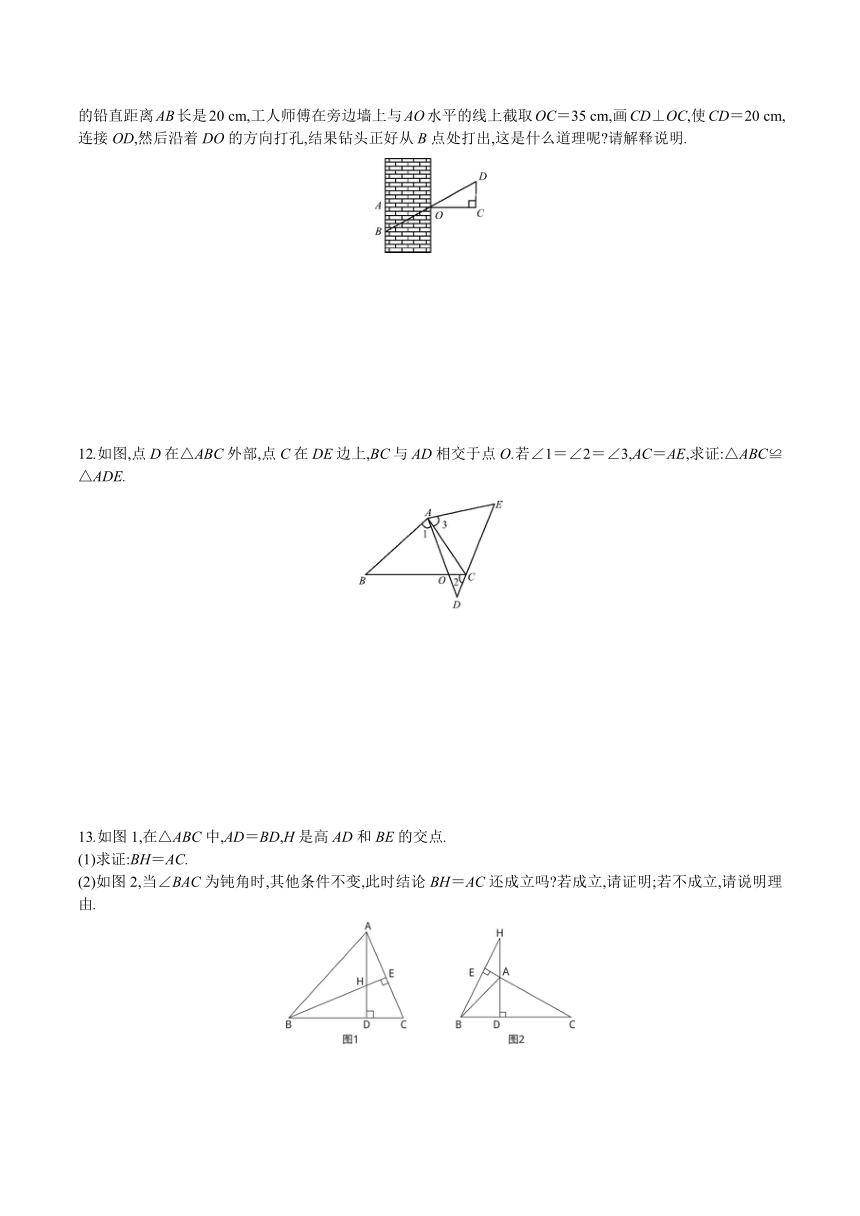
11.如图,工人师傅要在墙壁的O处用钻打孔,要使孔口从墙壁对面的B点处打出,墙壁厚是35 cm,B点与O点的铅直距离AB长是20 cm,工人师傅在旁边墙上与AO水平的线上截取OC=35 cm,画CD⊥OC,使CD=20 cm,连接OD,然后沿着DO的方向打孔,结果钻头正好从B点处打出,这是什么道理呢?请解释说明.
12.如图,点D在△ABC外部,点C在DE边上,BC与AD相交于点O.若∠1=∠2=∠3,AC=AE,求证:△ABC≌△ADE.
13.如图1,在△ABC中,AD=BD,H是高AD和BE的交点.
(1)求证:BH=AC.
(2)如图2,当∠BAC为钝角时,其他条件不变,此时结论BH=AC还成立吗?若成立,请证明;若不成立,请说明理由.
第3课时 利用两角一边判定三角形全等(ASA,AAS)
知识点1 三角形全等的判定方法(ASA)
1.如图,已知∠1=∠2,则不一定能使△ABC≌△ABD的条件是( B )
A.AC=AD B.BC=BD
C.∠C=∠D D.∠3=∠4
第1题图 第2题图
2.如图,线段AB,CD相交于点O,AO=BO.若用“ASA”判定△AOC≌△BOD,还需要添加的一个条件是 ∠A=∠B(答案不唯一) .?
3.如图,∠ABC=∠DCB,∠ACB=∠DBC.求证:△ABC≌△DCB.
证明:在△ABC和△DCB中,∠ABC=∠DCB,BC=CB,∠ACB=∠DBC,
∴△ABC≌△DCB(ASA).
知识点2 三角形全等的判定方法(AAS)
4.如图,在△ABC中,∠C=90°,D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E,则△ACB≌ △MDE ,判定依据是 AAS(答案不唯一) .(用字母表示)?
第4题图 第5题图
5.如图,太阳光线AC与A'C'是平行的,同一时刻两根高度相同且都垂直于地面的木杆在太阳光照射下的影子BC = B'C'.(填“>”“<”或“=”)?
知识点3 三角形全等的判定方法(ASA,AAS)的
综合应用
6.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①②③④),若要配块与原来大小一样的三角形玻璃,应该带( B )
A.第①块 B.第②块
C.第③块 D.第④块
第6题图 第7题图
7.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两张凳子之间(凳子与地面垂直).已知DC=a,CE=b,则两张凳子的高度之和为 a+b .?
8.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,则不能添加的一组条件是( C )
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
9.如图,AB⊥BC于点B,CD⊥BC于点C,且E为BC上一点,∠AED=90°,AE=DE,则判断△ABE≌△ECD的依据是 ASA或AAS .?
直角顶点在同一直线上的全等问题→面积关系问题
如图,直线l上有三个边长分别为a,b,c的正方形,若边长为a,c的正方形的面积分别为6和14,则边长为b的正方形的面积是 20 .?
10.如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点放在A点,两条直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是 16 .?
11.如图,工人师傅要在墙壁的O处用钻打孔,要使孔口从墙壁对面的B点处打出,墙壁厚是35 cm,B点与O点的铅直距离AB长是20 cm,工人师傅在旁边墙上与AO水平的线上截取OC=35 cm,画CD⊥OC,使CD=20 cm,连接OD,然后沿着DO的方向打孔,结果钻头正好从B点处打出,这是什么道理呢?请解释说明.
解:∵OC=35 cm,墙壁厚OA=35 cm,
∴OC=OA.
∵墙体是垂直的,∴∠OAB=90°且CD⊥OC,
∴∠OAB=∠OCD=90°.
在△OAB和△OCD中,∠OAB=∠OCD,OC=OA,∠AOB=∠COD,
∴△OAB≌△OCD(ASA),∴CD=AB.
∵CD=20 cm,∴AB=20 cm,
∴钻头正好从B点处打出.
12.如图,点D在△ABC外部,点C在DE边上,BC与AD相交于点O.若∠1=∠2=∠3,AC=AE,求证:△ABC≌△ADE.
证明:∵∠1=∠3,∴∠BAC=∠DAE.
∵∠B=∠180°-∠1-∠AOB,∠D=180°-∠2-∠COD,
且∠1=∠2,∠AOB=∠COD,∴∠B=∠D.
在△ABC和△ADE中,∠B=∠D,∠BAC=∠DAE,AC=AE,
∴△ABC≌△ADE(AAS).
13.如图1,在△ABC中,AD=BD,H是高AD和BE的交点.
(1)求证:BH=AC.
(2)如图2,当∠BAC为钝角时,其他条件不变,此时结论BH=AC还成立吗?若成立,请证明;若不成立,请说明理由.
解:(1)∵AD⊥BC,BE⊥AC,∴∠ADC=90°,∠BEC=90°,
∴∠DAC+∠C=90°,∠EBC+∠C=90°,
∴∠DAC=∠EBC.易证△BDH≌△ADC,
∴BH=AC.
(2)BH=AC仍然成立.
理由:∵AD⊥BC,BE⊥AC,
∴∠ADB=∠AEB=90°,
∴∠CBE+∠C=90°,∠CBE+∠BHD=90°,
∴∠BHD=∠C.
在△BDH和△ADC中,∠BHD=∠C,∠BDH=∠ADC,BD=AD,
∴△BDH≌△ADC(AAS),∴BH=AC.
知识点1 三角形全等的判定方法(ASA)
1.如图,已知∠1=∠2,则不一定能使△ABC≌△ABD的条件是( )
A.AC=AD B.BC=BD
C.∠C=∠D D.∠3=∠4
第1题图 第2题图
2.如图,线段AB,CD相交于点O,AO=BO.若用“ASA”判定△AOC≌△BOD,还需要添加的一个条件是 .?
3.如图,∠ABC=∠DCB,∠ACB=∠DBC.求证:△ABC≌△DCB.
知识点2 三角形全等的判定方法(AAS)
4.如图,在△ABC中,∠C=90°,D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E,则△ACB≌ ,判定依据是 .(用字母表示)?
第4题图 第5题图
5.如图,太阳光线AC与A'C'是平行的,同一时刻两根高度相同且都垂直于地面的木杆在太阳光照射下的影子BC B'C'.(填“>”“<”或“=”)?
知识点3 三角形全等的判定方法(ASA,AAS)的
综合应用
6.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①②③④),若要配块与原来大小一样的三角形玻璃,应该带( )
A.第①块 B.第②块
C.第③块 D.第④块
第6题图 第7题图
7.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两张凳子之间(凳子与地面垂直).已知DC=a,CE=b,则两张凳子的高度之和为 .?
8.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,则不能添加的一组条件是( )
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
9.如图,AB⊥BC于点B,CD⊥BC于点C,且E为BC上一点,∠AED=90°,AE=DE,则判断△ABE≌△ECD的依据是 .?
直角顶点在同一直线上的全等问题→面积关系问题
如图,直线l上有三个边长分别为a,b,c的正方形,若边长为a,c的正方形的面积分别为6和14,则边长为b的正方形的面积是 .?
10.如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点放在A点,两条直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是 .?
11.如图,工人师傅要在墙壁的O处用钻打孔,要使孔口从墙壁对面的B点处打出,墙壁厚是35 cm,B点与O点的铅直距离AB长是20 cm,工人师傅在旁边墙上与AO水平的线上截取OC=35 cm,画CD⊥OC,使CD=20 cm,连接OD,然后沿着DO的方向打孔,结果钻头正好从B点处打出,这是什么道理呢?请解释说明.
12.如图,点D在△ABC外部,点C在DE边上,BC与AD相交于点O.若∠1=∠2=∠3,AC=AE,求证:△ABC≌△ADE.
13.如图1,在△ABC中,AD=BD,H是高AD和BE的交点.
(1)求证:BH=AC.
(2)如图2,当∠BAC为钝角时,其他条件不变,此时结论BH=AC还成立吗?若成立,请证明;若不成立,请说明理由.
第3课时 利用两角一边判定三角形全等(ASA,AAS)
知识点1 三角形全等的判定方法(ASA)
1.如图,已知∠1=∠2,则不一定能使△ABC≌△ABD的条件是( B )
A.AC=AD B.BC=BD
C.∠C=∠D D.∠3=∠4
第1题图 第2题图
2.如图,线段AB,CD相交于点O,AO=BO.若用“ASA”判定△AOC≌△BOD,还需要添加的一个条件是 ∠A=∠B(答案不唯一) .?
3.如图,∠ABC=∠DCB,∠ACB=∠DBC.求证:△ABC≌△DCB.
证明:在△ABC和△DCB中,∠ABC=∠DCB,BC=CB,∠ACB=∠DBC,
∴△ABC≌△DCB(ASA).
知识点2 三角形全等的判定方法(AAS)
4.如图,在△ABC中,∠C=90°,D是AB边上的一点,DM⊥AB,且DM=AC,过点M作ME∥BC交AB于点E,则△ACB≌ △MDE ,判定依据是 AAS(答案不唯一) .(用字母表示)?
第4题图 第5题图
5.如图,太阳光线AC与A'C'是平行的,同一时刻两根高度相同且都垂直于地面的木杆在太阳光照射下的影子BC = B'C'.(填“>”“<”或“=”)?
知识点3 三角形全等的判定方法(ASA,AAS)的
综合应用
6.花花不慎将一块三角形的玻璃打碎成了如图所示的四块(图中所标①②③④),若要配块与原来大小一样的三角形玻璃,应该带( B )
A.第①块 B.第②块
C.第③块 D.第④块
第6题图 第7题图
7.如图,课间小明拿着老师的等腰三角板玩,不小心掉到两张凳子之间(凳子与地面垂直).已知DC=a,CE=b,则两张凳子的高度之和为 a+b .?
8.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,则不能添加的一组条件是( C )
A.BC=EC,∠B=∠E
B.BC=EC,AC=DC
C.BC=DC,∠A=∠D
D.∠B=∠E,∠A=∠D
9.如图,AB⊥BC于点B,CD⊥BC于点C,且E为BC上一点,∠AED=90°,AE=DE,则判断△ABE≌△ECD的依据是 ASA或AAS .?
直角顶点在同一直线上的全等问题→面积关系问题
如图,直线l上有三个边长分别为a,b,c的正方形,若边长为a,c的正方形的面积分别为6和14,则边长为b的正方形的面积是 20 .?
10.如图,有一块边长为4的正方形塑料模板ABCD,将一块足够大的直角三角板的直角顶点放在A点,两条直角边分别与CD交于点F,与CB的延长线交于点E,则四边形AECF的面积是 16 .?
11.如图,工人师傅要在墙壁的O处用钻打孔,要使孔口从墙壁对面的B点处打出,墙壁厚是35 cm,B点与O点的铅直距离AB长是20 cm,工人师傅在旁边墙上与AO水平的线上截取OC=35 cm,画CD⊥OC,使CD=20 cm,连接OD,然后沿着DO的方向打孔,结果钻头正好从B点处打出,这是什么道理呢?请解释说明.
解:∵OC=35 cm,墙壁厚OA=35 cm,
∴OC=OA.
∵墙体是垂直的,∴∠OAB=90°且CD⊥OC,
∴∠OAB=∠OCD=90°.
在△OAB和△OCD中,∠OAB=∠OCD,OC=OA,∠AOB=∠COD,
∴△OAB≌△OCD(ASA),∴CD=AB.
∵CD=20 cm,∴AB=20 cm,
∴钻头正好从B点处打出.
12.如图,点D在△ABC外部,点C在DE边上,BC与AD相交于点O.若∠1=∠2=∠3,AC=AE,求证:△ABC≌△ADE.
证明:∵∠1=∠3,∴∠BAC=∠DAE.
∵∠B=∠180°-∠1-∠AOB,∠D=180°-∠2-∠COD,
且∠1=∠2,∠AOB=∠COD,∴∠B=∠D.
在△ABC和△ADE中,∠B=∠D,∠BAC=∠DAE,AC=AE,
∴△ABC≌△ADE(AAS).
13.如图1,在△ABC中,AD=BD,H是高AD和BE的交点.
(1)求证:BH=AC.
(2)如图2,当∠BAC为钝角时,其他条件不变,此时结论BH=AC还成立吗?若成立,请证明;若不成立,请说明理由.
解:(1)∵AD⊥BC,BE⊥AC,∴∠ADC=90°,∠BEC=90°,
∴∠DAC+∠C=90°,∠EBC+∠C=90°,
∴∠DAC=∠EBC.易证△BDH≌△ADC,
∴BH=AC.
(2)BH=AC仍然成立.
理由:∵AD⊥BC,BE⊥AC,
∴∠ADB=∠AEB=90°,
∴∠CBE+∠C=90°,∠CBE+∠BHD=90°,
∴∠BHD=∠C.
在△BDH和△ADC中,∠BHD=∠C,∠BDH=∠ADC,BD=AD,
∴△BDH≌△ADC(AAS),∴BH=AC.
