2020-2021学年人教版九年级数学下册27.2 相似三角形同步练习(Word版,含答案)
文档属性
| 名称 | 2020-2021学年人教版九年级数学下册27.2 相似三角形同步练习(Word版,含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 345.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 16:33:28 | ||
图片预览



文档简介
《27.2 相似三角形》同步练习2020-2021年数学人教版九(下)
一.选择题(共9小题)
1.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
A. B.
C. D.
2.如图,在大小为4×4的正方形网格中,是相似三角形的是( )
A.①② B.②③ C.①③ D.②④
3.以下各图放置的小正方形的边长都相同,分别以小正方形的顶点为顶点画三角形,则与△ABC相似的三角形图形为( )
A. B. C. D.
4.如图,在?ABCD中,AB=5,BC=8,∠ABC,∠BCD的角平分线分别交AD于E和F,BE与CF交于点G,则△EFG与△BCG面积之比是( )
A.5:8 B.25:64 C.1:4 D.1:16
5.两个相似多边形的相似比是2:3,则这两个多边形的周长比是( )
A.4:9 B. C.2:5 D.2:3
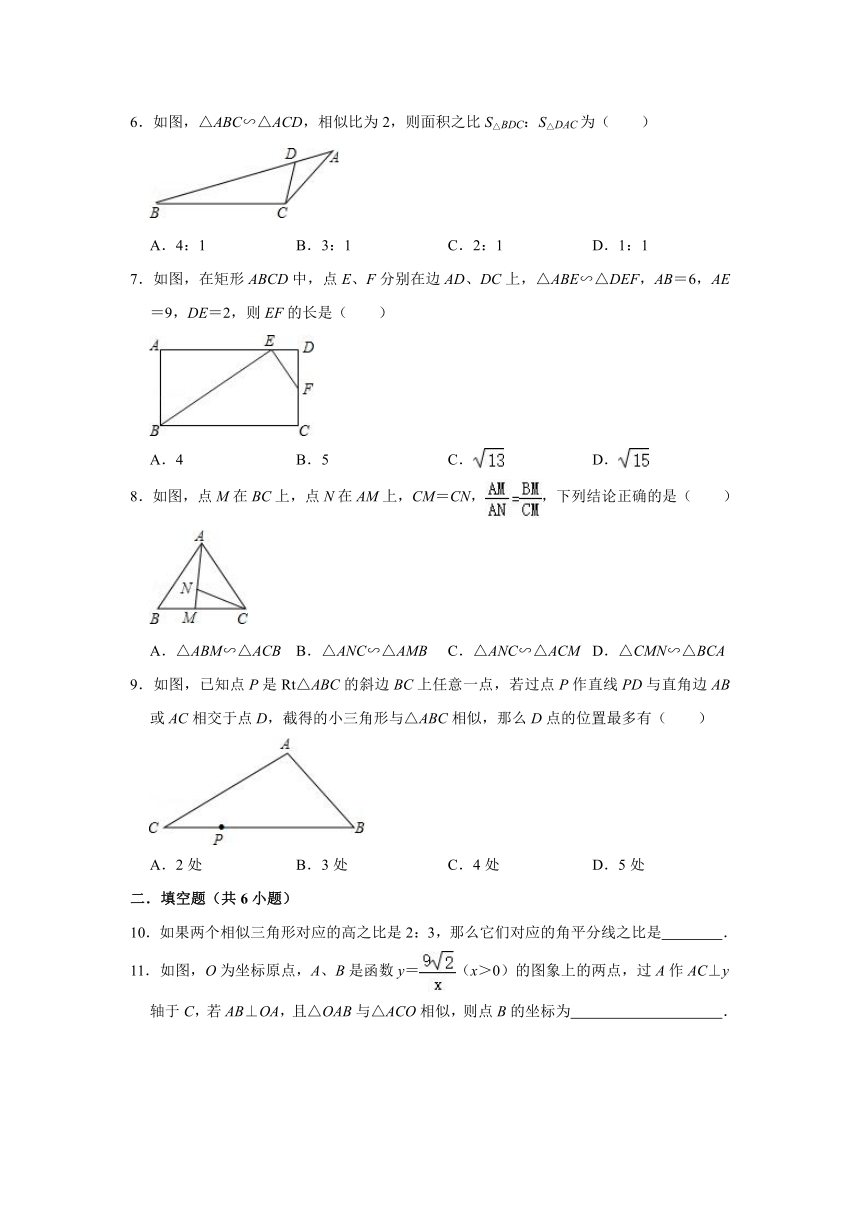
6.如图,△ABC∽△ACD,相似比为2,则面积之比S△BDC:S△DAC为( )
A.4:1 B.3:1 C.2:1 D.1:1
7.如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,则EF的长是( )
A.4 B.5 C. D.
8.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )
A.△ABM∽△ACB B.△ANC∽△AMB C.△ANC∽△ACM D.△CMN∽△BCA
9.如图,已知点P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么D点的位置最多有( )
A.2处 B.3处 C.4处 D.5处
二.填空题(共6小题)
10.如果两个相似三角形对应的高之比是2:3,那么它们对应的角平分线之比是 .
11.如图,O为坐标原点,A、B是函数y=(x>0)的图象上的两点,过A作AC⊥y轴于C,若AB⊥OA,且△OAB与△ACO相似,则点B的坐标为 .
12.在上午的某一时刻身高1.7米的小刚在地面上的投影长为3.4米,小明测得校园中旗杆在地面上的影子长16米,还有2米影子落在墙上,根据这些条件可以知道旗杆的高度为 米.
13.如图,已知直角△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD= .
14.已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AD=8,BD=2,那么CD= .
15.在Rt△ABC中,C为直角顶点,过点C作AB的垂线,若D为垂足,若AC、BC为方程x2﹣6x+2=0的两根,则AD?BD的值等于 .
三.解答题(共9小题)
16.已知△ABC中,点D在BC边上,且AD平分∠BAC,过点C作AB的平行线与AD的延长线交于点E.
(1)求证:△ABD∽△ECD;
(2)求证:=.
17.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
18.如图,在△ABC中,AC=8厘米,BC=16厘米,点P从点A出发,沿着AC边向点C以1cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC和△ABC相似?
19.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
20.如图1,在△ABC中,AB=AC=10,BC=12.
(1)求AC边上的高BH的长;
(2)如图2,点D、E分别在边AB、BC上,G、F在边AC上,当四边形DEGF是正方形时,求DE的长.
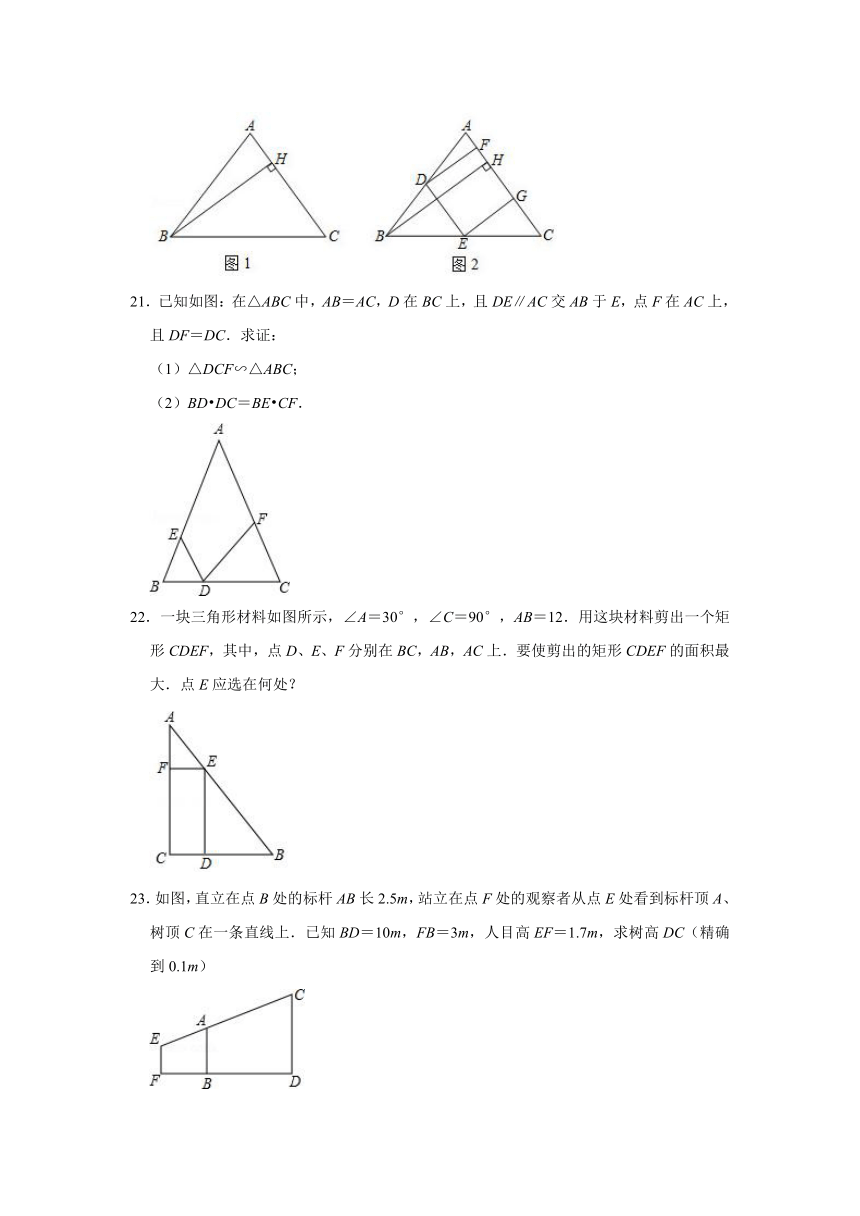
21.已知如图:在△ABC中,AB=AC,D在BC上,且DE∥AC交AB于E,点F在AC上,且DF=DC.求证:
(1)△DCF∽△ABC;
(2)BD?DC=BE?CF.
22.一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12.用这块材料剪出一个矩形CDEF,其中,点D、E、F分别在BC,AB,AC上.要使剪出的矩形CDEF的面积最大.点E应选在何处?
23.如图,直立在点B处的标杆AB长2.5m,站立在点F处的观察者从点E处看到标杆顶A、树顶C在一条直线上.已知BD=10m,FB=3m,人目高EF=1.7m,求树高DC(精确到0.1m)
24.已知图1和图2中的每个小正方形的边长都是1个单位.
(1)将图1中的格点△ABC,先向右平移3个单位,再向上平移2个单位,得到△A1B1C1,请你在图1中画出△A1B1C1;
(2)在图2中画出一个与格点△DEF相似但相似比不等于1的格点三角形.
参考答案
一.选择题(共9小题)
1.解:根据题意得:AB==,AC=2,BC==,
∴BC:AC:AB=1::,
A、三边之比为1::,图中的三角形(阴影部分)与△ABC相似;
B、三边之比::3,图中的三角形(阴影部分)与△ABC不相似;
C、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.
故选:A.
2.解:∵①中的三角形的三边分别是:2,,,
②中的三角形的三边分别是:3,,,
③中的三角形的三边分别是:2,2,2,
④中的三角形的三边分别是:3,,4,
∵①与③中的三角形的三边的比为:1:,
∴①与③相似.
故选:C.
3.解:设每个小正方形的边长为1,则△ABC的各边长分别为:2,,,同理求得:
A中三角形的各边长为:,1,,与△ABC的各边对应成比例,所以两三角形相似;
故选:A.
4.解:∵BE、CF分别为∠ABC,∠BCD的角平分线,
∴AE=AB,DF=CD,
又AB=5,BC=8,∴AF=DE=3,EF=2,
∴===,
故选:D.
5.解:∵两个相似多边形的相似比是2:3,
∴这两个多边形的周长为2:3.
故选:D.
6.解:∵△ABC∽△ACD,相似比为2,
∴S△ABC:S△ACD=4,
∴S△BDC:S△ACD=3:1.
故选:B.
7.解:∵△ABE∽△DEF,
∴,
∵AB=6,AE=9,DE=2,
∴,
解得:DF=3,
∵四边形ABCD是矩形,
∴∠D=90°,
∴EF==.
故选:C.
8.解:∵CM=CN
∴∠CNM=∠CMN
∵∠CNA=∠CMN+∠MCN,∠AMB=∠CNM+∠MCN
∴∠CNA=∠AMB
∵AM:AN=BM:CM
∴AM:AN=BM:CN
∴△ANC∽△AMB
故选:B.
9.
解:∵截得的小三角形与△ABC相似,
∴过P作AC的垂线,作AB的垂线,作BC的垂线,所截得的三角形满足题意,
则D点的位置最多有3处,
故选:B.
二.填空题(共6小题)
10.解:∵相似三角形对应高线的比是2:3,
∴它们的相似比为2:3,
∴它们对应角平分线的比是2:3.
故答案为:2:3.
11.解:∵△OAB∽△ACO,
∴∠AOC=∠BOA,
∴OA是∠BOC的平分线,
延长BA交y轴于D,过B作BE⊥y轴于E,
∵AC⊥OC,
∴AC∥BE,
∵AB⊥OA,
∴AB=AD,
设A(a,),
∴AC2=CD?OC,
∴CD=,
∴CE=CD=,
∴OE=﹣,
BE=2AC=2a,
∴B(2a,﹣),
∴2a(﹣)=9,
解得:a=3,(负值舍去),
∴点B的坐标为(6,).
故答案为:(6,).
12.解:∵==,
∵CE=2,
∴CD=4,
∴BD=BC+CD=16+4=20米.
∴AB=BD=×20=10米.
故应填10.
13.解:在Rt△ABC中,AB==5,
由射影定理得,AC2=AD?AB,
∴AD==,
故答案为:.
14.解:由射影定理得,CD2=AD?DB,
则CD==4,
故答案为:4.
15.解:∵AC、BC为方程x2﹣6x+2=0的两根,
∴x1=,x2=,
令AC=,BC=,
∴AB==4,
又AB×CD=AC×BC,
∴CD===,
∴AD?BD=CD2==.
故答案为:.
三.解答题(共9小题)
16.证明:(1)∵CE∥AB,
∴∠BAD=∠CED、∠ABD=∠ECD,
∴△ABD∽△ECD;
(2)∵AD平分∠BAC,
∴∠BAD=∠EAC,
又∵∠BAD=∠CED,
∴∠CEA=∠CAE,
∴CA=CE,
∵△ABD∽△ECD,
∴=,
∴=.
17.解:设经x秒钟△PBQ与△ABC相似,
则AP=2xcm,BQ=4xcm,
∵AB=8cm,BC=16cm,
∴BP=AB﹣AP=(8﹣2x)cm,
∵∠B是公共角,
∵①当,即时,△PBQ∽△ABC,
解得:x=2;
②当,即时,△QBP∽△ABC,
解得:x=0.8,
∴经2或0.8秒钟△PBQ与△ABC相似.
18.解:设经过x秒,两三角形相似,
则CP=AC﹣AP=8﹣x,CQ=2x,
(1)当CP与CA是对应边时,,
即,
解得x=4秒;
(2)当CP与BC是对应边时,,
即,
解得x=秒;
故经过4或秒,两个三角形相似.
19.证明:在△ABC中,AB=AC,BD=CD,
∴AD⊥BC,
∵CE⊥AB,
∴∠ADB=∠CEB=90°,
又∵∠B=∠B,
∴△ABD∽△CBE.
20.解:(1)过点A作AN⊥BC于N,
∵AB=AC=10,BC=12,AN⊥BC,
∴BN=CN=6,
∴AN===8,
∵S△ABC=AC×BH=BC×AN,
∴BH==9.6;
(2)如图2,设BH与DE交于点M,
∵四边形DEGF是正方形,
∴DE=EG=DF,DE∥AC,∠EDF=∠DFC=90°,且BH⊥AC,
∴四边形DFHM是矩形,
∴DF=MH,
∵DE∥AC,
∴△BDE∽△BAC,
∴,
∴
∴DE=.
21.证明:
(1)在△ABC中,AB=AC,
∴∠B=∠C.
∵DF=DC,
∴∠C=∠CFD.
∴∠B=∠CFD.
∴△DCF∽△ABC.
(2)证明△BDE∽△CFD.
∵DE∥AC,
∴∠EDB=∠C.
∴∠B=∠CFD.
∴△BDE∽△CFD.
∴BD:CF=BE:CD.
∴BD?DC=BE?CF.
22.解:∵四边形CDEF是矩形,
∴∠AFE=90°,
∵∠A=30°,
∴EF=AE,
在Rt△ABC中,∠C=90°,AB=12,
∴BC=AB=6,
根据勾股定理得:AC==6,
∴CF=AC﹣AF=6﹣AE,
∴S矩形CDEF=CF?EF=AE(6﹣AE)=﹣(AE﹣6)2+9,
∴当x=6时,矩形CDEF的面积最大,
即当点E为AB的中点时,矩形CDEF的面积最大.
23.解:过E作EH⊥CD交CD于H点,交AB于点G,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB
∴四边形EFDH为矩形
∴EF=GB=DH=1.7,EG=FB=3,GH=BD=10
∴AG=AB﹣GB=0.8
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH
∴
∵EH=EG+GH=13
∴CH=≈3.5
∴CD=CH+HD=5.2
答:故树高DC为5.2米.
24.解:(1)如图1.
(2)如图2.
(答案不唯一.)
一.选择题(共9小题)
1.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC相似的是( )
A. B.
C. D.
2.如图,在大小为4×4的正方形网格中,是相似三角形的是( )
A.①② B.②③ C.①③ D.②④
3.以下各图放置的小正方形的边长都相同,分别以小正方形的顶点为顶点画三角形,则与△ABC相似的三角形图形为( )
A. B. C. D.
4.如图,在?ABCD中,AB=5,BC=8,∠ABC,∠BCD的角平分线分别交AD于E和F,BE与CF交于点G,则△EFG与△BCG面积之比是( )
A.5:8 B.25:64 C.1:4 D.1:16
5.两个相似多边形的相似比是2:3,则这两个多边形的周长比是( )
A.4:9 B. C.2:5 D.2:3
6.如图,△ABC∽△ACD,相似比为2,则面积之比S△BDC:S△DAC为( )
A.4:1 B.3:1 C.2:1 D.1:1
7.如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,则EF的长是( )
A.4 B.5 C. D.
8.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )
A.△ABM∽△ACB B.△ANC∽△AMB C.△ANC∽△ACM D.△CMN∽△BCA
9.如图,已知点P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么D点的位置最多有( )
A.2处 B.3处 C.4处 D.5处
二.填空题(共6小题)
10.如果两个相似三角形对应的高之比是2:3,那么它们对应的角平分线之比是 .
11.如图,O为坐标原点,A、B是函数y=(x>0)的图象上的两点,过A作AC⊥y轴于C,若AB⊥OA,且△OAB与△ACO相似,则点B的坐标为 .
12.在上午的某一时刻身高1.7米的小刚在地面上的投影长为3.4米,小明测得校园中旗杆在地面上的影子长16米,还有2米影子落在墙上,根据这些条件可以知道旗杆的高度为 米.
13.如图,已知直角△ABC中,CD是斜边AB上的高,AC=4,BC=3,则AD= .
14.已知:如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AD=8,BD=2,那么CD= .
15.在Rt△ABC中,C为直角顶点,过点C作AB的垂线,若D为垂足,若AC、BC为方程x2﹣6x+2=0的两根,则AD?BD的值等于 .
三.解答题(共9小题)
16.已知△ABC中,点D在BC边上,且AD平分∠BAC,过点C作AB的平行线与AD的延长线交于点E.
(1)求证:△ABD∽△ECD;
(2)求证:=.
17.如图,在△ABC中,AB=8cm,BC=16cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从点B开始沿边BC向点C以4cm/s的速度移动,如果点P、Q分别从点A、B同时出发,经几秒钟△PBQ与△ABC相似?试说明理由.
18.如图,在△ABC中,AC=8厘米,BC=16厘米,点P从点A出发,沿着AC边向点C以1cm/s的速度运动,点Q从点C出发,沿着CB边向点B以2cm/s的速度运动,如果P与Q同时出发,经过几秒△PQC和△ABC相似?
19.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.
20.如图1,在△ABC中,AB=AC=10,BC=12.
(1)求AC边上的高BH的长;
(2)如图2,点D、E分别在边AB、BC上,G、F在边AC上,当四边形DEGF是正方形时,求DE的长.
21.已知如图:在△ABC中,AB=AC,D在BC上,且DE∥AC交AB于E,点F在AC上,且DF=DC.求证:
(1)△DCF∽△ABC;
(2)BD?DC=BE?CF.
22.一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12.用这块材料剪出一个矩形CDEF,其中,点D、E、F分别在BC,AB,AC上.要使剪出的矩形CDEF的面积最大.点E应选在何处?
23.如图,直立在点B处的标杆AB长2.5m,站立在点F处的观察者从点E处看到标杆顶A、树顶C在一条直线上.已知BD=10m,FB=3m,人目高EF=1.7m,求树高DC(精确到0.1m)
24.已知图1和图2中的每个小正方形的边长都是1个单位.
(1)将图1中的格点△ABC,先向右平移3个单位,再向上平移2个单位,得到△A1B1C1,请你在图1中画出△A1B1C1;
(2)在图2中画出一个与格点△DEF相似但相似比不等于1的格点三角形.
参考答案
一.选择题(共9小题)
1.解:根据题意得:AB==,AC=2,BC==,
∴BC:AC:AB=1::,
A、三边之比为1::,图中的三角形(阴影部分)与△ABC相似;
B、三边之比::3,图中的三角形(阴影部分)与△ABC不相似;
C、三边之比为1::2,图中的三角形(阴影部分)与△ABC不相似;
D、三边之比为2::,图中的三角形(阴影部分)与△ABC不相似.
故选:A.
2.解:∵①中的三角形的三边分别是:2,,,
②中的三角形的三边分别是:3,,,
③中的三角形的三边分别是:2,2,2,
④中的三角形的三边分别是:3,,4,
∵①与③中的三角形的三边的比为:1:,
∴①与③相似.
故选:C.
3.解:设每个小正方形的边长为1,则△ABC的各边长分别为:2,,,同理求得:
A中三角形的各边长为:,1,,与△ABC的各边对应成比例,所以两三角形相似;
故选:A.
4.解:∵BE、CF分别为∠ABC,∠BCD的角平分线,
∴AE=AB,DF=CD,
又AB=5,BC=8,∴AF=DE=3,EF=2,
∴===,
故选:D.
5.解:∵两个相似多边形的相似比是2:3,
∴这两个多边形的周长为2:3.
故选:D.
6.解:∵△ABC∽△ACD,相似比为2,
∴S△ABC:S△ACD=4,
∴S△BDC:S△ACD=3:1.
故选:B.
7.解:∵△ABE∽△DEF,
∴,
∵AB=6,AE=9,DE=2,
∴,
解得:DF=3,
∵四边形ABCD是矩形,
∴∠D=90°,
∴EF==.
故选:C.
8.解:∵CM=CN
∴∠CNM=∠CMN
∵∠CNA=∠CMN+∠MCN,∠AMB=∠CNM+∠MCN
∴∠CNA=∠AMB
∵AM:AN=BM:CM
∴AM:AN=BM:CN
∴△ANC∽△AMB
故选:B.
9.
解:∵截得的小三角形与△ABC相似,
∴过P作AC的垂线,作AB的垂线,作BC的垂线,所截得的三角形满足题意,
则D点的位置最多有3处,
故选:B.
二.填空题(共6小题)
10.解:∵相似三角形对应高线的比是2:3,
∴它们的相似比为2:3,
∴它们对应角平分线的比是2:3.
故答案为:2:3.
11.解:∵△OAB∽△ACO,
∴∠AOC=∠BOA,
∴OA是∠BOC的平分线,
延长BA交y轴于D,过B作BE⊥y轴于E,
∵AC⊥OC,
∴AC∥BE,
∵AB⊥OA,
∴AB=AD,
设A(a,),
∴AC2=CD?OC,
∴CD=,
∴CE=CD=,
∴OE=﹣,
BE=2AC=2a,
∴B(2a,﹣),
∴2a(﹣)=9,
解得:a=3,(负值舍去),
∴点B的坐标为(6,).
故答案为:(6,).
12.解:∵==,
∵CE=2,
∴CD=4,
∴BD=BC+CD=16+4=20米.
∴AB=BD=×20=10米.
故应填10.
13.解:在Rt△ABC中,AB==5,
由射影定理得,AC2=AD?AB,
∴AD==,
故答案为:.
14.解:由射影定理得,CD2=AD?DB,
则CD==4,
故答案为:4.
15.解:∵AC、BC为方程x2﹣6x+2=0的两根,
∴x1=,x2=,
令AC=,BC=,
∴AB==4,
又AB×CD=AC×BC,
∴CD===,
∴AD?BD=CD2==.
故答案为:.
三.解答题(共9小题)
16.证明:(1)∵CE∥AB,
∴∠BAD=∠CED、∠ABD=∠ECD,
∴△ABD∽△ECD;
(2)∵AD平分∠BAC,
∴∠BAD=∠EAC,
又∵∠BAD=∠CED,
∴∠CEA=∠CAE,
∴CA=CE,
∵△ABD∽△ECD,
∴=,
∴=.
17.解:设经x秒钟△PBQ与△ABC相似,
则AP=2xcm,BQ=4xcm,
∵AB=8cm,BC=16cm,
∴BP=AB﹣AP=(8﹣2x)cm,
∵∠B是公共角,
∵①当,即时,△PBQ∽△ABC,
解得:x=2;
②当,即时,△QBP∽△ABC,
解得:x=0.8,
∴经2或0.8秒钟△PBQ与△ABC相似.
18.解:设经过x秒,两三角形相似,
则CP=AC﹣AP=8﹣x,CQ=2x,
(1)当CP与CA是对应边时,,
即,
解得x=4秒;
(2)当CP与BC是对应边时,,
即,
解得x=秒;
故经过4或秒,两个三角形相似.
19.证明:在△ABC中,AB=AC,BD=CD,
∴AD⊥BC,
∵CE⊥AB,
∴∠ADB=∠CEB=90°,
又∵∠B=∠B,
∴△ABD∽△CBE.
20.解:(1)过点A作AN⊥BC于N,
∵AB=AC=10,BC=12,AN⊥BC,
∴BN=CN=6,
∴AN===8,
∵S△ABC=AC×BH=BC×AN,
∴BH==9.6;
(2)如图2,设BH与DE交于点M,
∵四边形DEGF是正方形,
∴DE=EG=DF,DE∥AC,∠EDF=∠DFC=90°,且BH⊥AC,
∴四边形DFHM是矩形,
∴DF=MH,
∵DE∥AC,
∴△BDE∽△BAC,
∴,
∴
∴DE=.
21.证明:
(1)在△ABC中,AB=AC,
∴∠B=∠C.
∵DF=DC,
∴∠C=∠CFD.
∴∠B=∠CFD.
∴△DCF∽△ABC.
(2)证明△BDE∽△CFD.
∵DE∥AC,
∴∠EDB=∠C.
∴∠B=∠CFD.
∴△BDE∽△CFD.
∴BD:CF=BE:CD.
∴BD?DC=BE?CF.
22.解:∵四边形CDEF是矩形,
∴∠AFE=90°,
∵∠A=30°,
∴EF=AE,
在Rt△ABC中,∠C=90°,AB=12,
∴BC=AB=6,
根据勾股定理得:AC==6,
∴CF=AC﹣AF=6﹣AE,
∴S矩形CDEF=CF?EF=AE(6﹣AE)=﹣(AE﹣6)2+9,
∴当x=6时,矩形CDEF的面积最大,
即当点E为AB的中点时,矩形CDEF的面积最大.
23.解:过E作EH⊥CD交CD于H点,交AB于点G,如下图所示:
由已知得,EF⊥FD,AB⊥FD,CD⊥FD,
∵EH⊥CD,EH⊥AB
∴四边形EFDH为矩形
∴EF=GB=DH=1.7,EG=FB=3,GH=BD=10
∴AG=AB﹣GB=0.8
∵EH⊥CD,EH⊥AB,
∴AG∥CH,
∴△AEG∽△CEH
∴
∵EH=EG+GH=13
∴CH=≈3.5
∴CD=CH+HD=5.2
答:故树高DC为5.2米.
24.解:(1)如图1.
(2)如图2.
(答案不唯一.)
