2021-2022学年人教版数学八年级上册12.1 全等三角形同步练习(Word版,含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册12.1 全等三角形同步练习(Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 140.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 16:35:29 | ||
图片预览

文档简介
第十二章 全等三角形
12.1 全等三角形
课堂笔记
1. 全等形的概念
(1)定义:能够 的两个图形叫做全等形.
(2)全等形的判别方法:两个图形形状相同大小相等→即完全重合.
2. 全等三角形的定义:能够 的两个三角形叫做全等三角形.
3. 两个三角形全等的记法:通常把表示对应顶点的字母写在对应的位置上,顺序不能随意书写.
4. 全等三角形的性质:全等三角形的对应边 ;全等三角形的对应角 .
分层训练
A组 基础训练
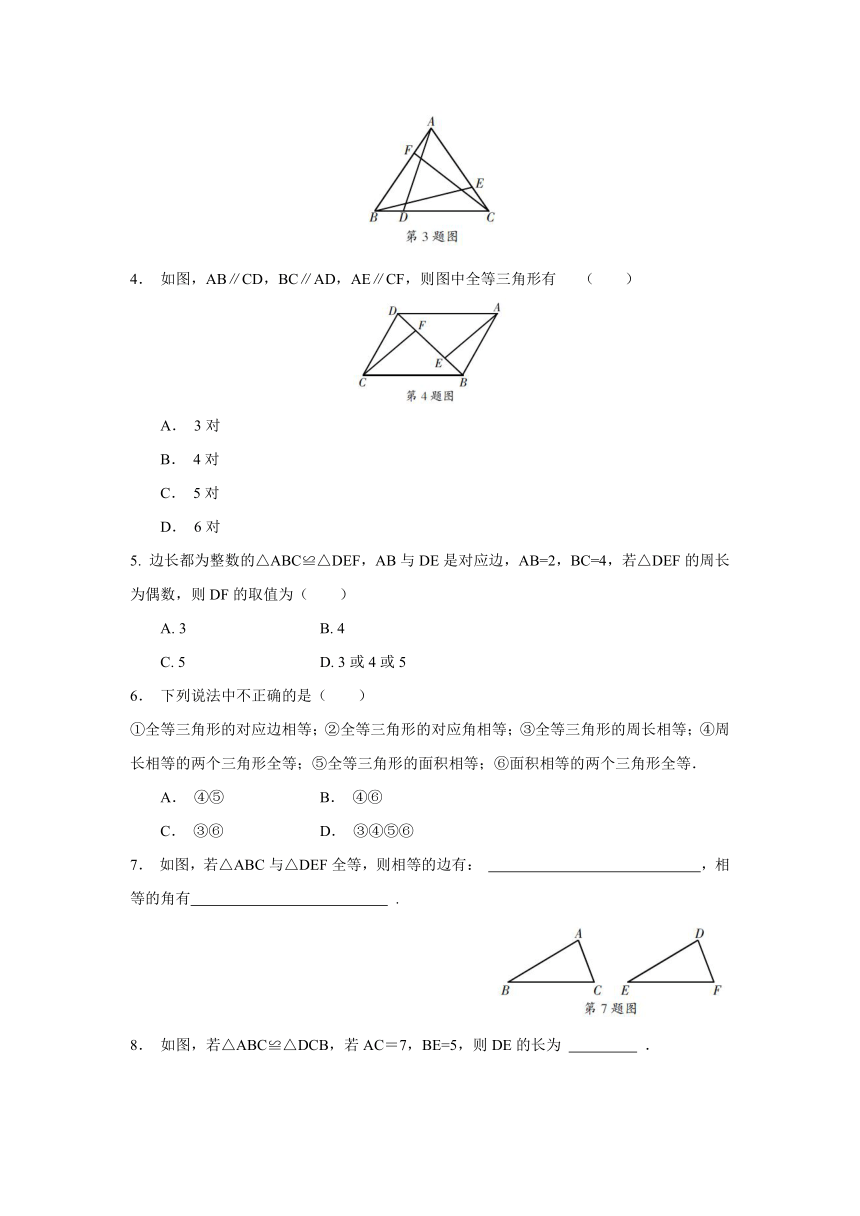
1. 已知图中的两个三角形全等,则∠α的度数是( )
A. 72° B. 60° C. 58° D. 50°
2. 如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A. 20° B. 30° C. 35° D. 40°
3. 如图,在等边△ABC中,取BD=CE=AF,且D,E,F非所在边中点,由图中找出3个全等三角形组成一组,这样的全等三角形的组数有( )
A. 2 B. 3
C. 4 D. 5
4. 如图,AB∥CD,BC∥AD,AE∥CF,则图中全等三角形有 ( )
A. 3对
B. 4对
C. 5对
D. 6对
5. 边长都为整数的△ABC≌△DEF,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为偶数,则DF的取值为( )
A. 3 B. 4
C. 5 D. 3或4或5
6. 下列说法中不正确的是( )
①全等三角形的对应边相等;②全等三角形的对应角相等;③全等三角形的周长相等;④周长相等的两个三角形全等;⑤全等三角形的面积相等;⑥面积相等的两个三角形全等.
A. ④⑤ B. ④⑥
C. ③⑥ D. ③④⑤⑥
7. 如图,若△ABC与△DEF全等,则相等的边有: ,相等的角有 .
8. 如图,若△ABC≌△DCB,若AC=7,BE=5,则DE的长为 .
9. 如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠ADC的度数为 .
10. 如图,△ABC≌△DEF,∠B=30°,∠A=50°,BF=2,求∠DFE的度数与EC的长.
B组 自主提高
11. 如图,△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠ACB=∠AED=105°,∠CAD=10°,∠B=∠D=25°,求∠DFB、∠DGB的度数.
12. 如图所示,△ADF≌△CBE,且点E,B,D,F在同一条直线上,判断AD与BC的位置关系,并说明理由.
13. 如图,A、D、E三点在同一直线上,且△BAD≌△ACE,试说明:
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
14. 如图,AB⊥BC,△ABE≌△ECD. 判断AE与DE的关系,并证明你的结论.
C组 综合运用
15. 如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P.
(1)若∠ABE=160°,∠DBC=30°,求∠CBE的度数;
(2)若AD=DC=3cm,BC=4.5cm,求△DCP与△BPE的周长之和.
参考答案
【课堂笔记】
1. (1)完全重合
2. 完全重合
4. 相等 相等
【分层训练】
1—5. DBDAB 6. B
7. AB=DE,AC=DF,BC=EF ∠A=∠D,∠B=∠E,∠C=∠F
8. 2
9. 130°
10. ∵△ABC≌△DEF,∴∠B=∠E=30°,∠D=∠A=50°,EF=BC,
∴∠DFE=180°-30°-50°=100°,EC=BF=2.
11. ∠DFB=∠B+∠DAB=85°,∠DGB=∠DFB-∠D=60°.
12. AD∥BC,理由如下:∵△ADF≌△CBE,∴∠ADF=∠CBE,∴∠3=∠4,∴AD∥BC.
13. (1)∵△BAD≌△ACE,∴BD=AE,AD=CE,∴BD=AE=CE+DE.
(2)当△ABD满足∠ADB=90°时,BD∥CE.
14. AE⊥ED且AE=DE. 证明:∵△ABE≌△ECD,∴AE=ED,∠A=∠DEC,∠AEB=∠D. ∵∠B=90°,∴∠A+∠AEB=90°. ∴∠DEC+∠AEB=90°. 即∠AED=90°,∴AE⊥ED且AE=DE.
15. (1)∵△ABC≌△DBE,∴∠ABC=∠DBE. ∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE. ∴∠CBE= 12(∠ABE-∠DBC)= 12×(160°-30°)=65°.
(2)∵△ABC≌△DBE,∴BE=BC=4.5cm,DE=AC=AD+DC=6cm.
∴△DCP与△BPE的周长之和为
DC+DP+PC+BP+PE+BE=(DP+PE)+(BP+PC)+DC+BE=DE+BC+DC+BE=6+4.5+3+4.5=18(cm).
12.1 全等三角形
课堂笔记
1. 全等形的概念
(1)定义:能够 的两个图形叫做全等形.
(2)全等形的判别方法:两个图形形状相同大小相等→即完全重合.
2. 全等三角形的定义:能够 的两个三角形叫做全等三角形.
3. 两个三角形全等的记法:通常把表示对应顶点的字母写在对应的位置上,顺序不能随意书写.
4. 全等三角形的性质:全等三角形的对应边 ;全等三角形的对应角 .
分层训练
A组 基础训练
1. 已知图中的两个三角形全等,则∠α的度数是( )
A. 72° B. 60° C. 58° D. 50°
2. 如图,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A. 20° B. 30° C. 35° D. 40°
3. 如图,在等边△ABC中,取BD=CE=AF,且D,E,F非所在边中点,由图中找出3个全等三角形组成一组,这样的全等三角形的组数有( )
A. 2 B. 3
C. 4 D. 5
4. 如图,AB∥CD,BC∥AD,AE∥CF,则图中全等三角形有 ( )
A. 3对
B. 4对
C. 5对
D. 6对
5. 边长都为整数的△ABC≌△DEF,AB与DE是对应边,AB=2,BC=4,若△DEF的周长为偶数,则DF的取值为( )
A. 3 B. 4
C. 5 D. 3或4或5
6. 下列说法中不正确的是( )
①全等三角形的对应边相等;②全等三角形的对应角相等;③全等三角形的周长相等;④周长相等的两个三角形全等;⑤全等三角形的面积相等;⑥面积相等的两个三角形全等.
A. ④⑤ B. ④⑥
C. ③⑥ D. ③④⑤⑥
7. 如图,若△ABC与△DEF全等,则相等的边有: ,相等的角有 .
8. 如图,若△ABC≌△DCB,若AC=7,BE=5,则DE的长为 .
9. 如图,△ABD≌△CBD,若∠A=80°,∠ABC=70°,则∠ADC的度数为 .
10. 如图,△ABC≌△DEF,∠B=30°,∠A=50°,BF=2,求∠DFE的度数与EC的长.
B组 自主提高
11. 如图,△ABC≌△ADE,BC的延长线交DA于F,交DE于G,∠ACB=∠AED=105°,∠CAD=10°,∠B=∠D=25°,求∠DFB、∠DGB的度数.
12. 如图所示,△ADF≌△CBE,且点E,B,D,F在同一条直线上,判断AD与BC的位置关系,并说明理由.
13. 如图,A、D、E三点在同一直线上,且△BAD≌△ACE,试说明:
(1)BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
14. 如图,AB⊥BC,△ABE≌△ECD. 判断AE与DE的关系,并证明你的结论.
C组 综合运用
15. 如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P.
(1)若∠ABE=160°,∠DBC=30°,求∠CBE的度数;
(2)若AD=DC=3cm,BC=4.5cm,求△DCP与△BPE的周长之和.
参考答案
【课堂笔记】
1. (1)完全重合
2. 完全重合
4. 相等 相等
【分层训练】
1—5. DBDAB 6. B
7. AB=DE,AC=DF,BC=EF ∠A=∠D,∠B=∠E,∠C=∠F
8. 2
9. 130°
10. ∵△ABC≌△DEF,∴∠B=∠E=30°,∠D=∠A=50°,EF=BC,
∴∠DFE=180°-30°-50°=100°,EC=BF=2.
11. ∠DFB=∠B+∠DAB=85°,∠DGB=∠DFB-∠D=60°.
12. AD∥BC,理由如下:∵△ADF≌△CBE,∴∠ADF=∠CBE,∴∠3=∠4,∴AD∥BC.
13. (1)∵△BAD≌△ACE,∴BD=AE,AD=CE,∴BD=AE=CE+DE.
(2)当△ABD满足∠ADB=90°时,BD∥CE.
14. AE⊥ED且AE=DE. 证明:∵△ABE≌△ECD,∴AE=ED,∠A=∠DEC,∠AEB=∠D. ∵∠B=90°,∴∠A+∠AEB=90°. ∴∠DEC+∠AEB=90°. 即∠AED=90°,∴AE⊥ED且AE=DE.
15. (1)∵△ABC≌△DBE,∴∠ABC=∠DBE. ∴∠ABC-∠DBC=∠DBE-∠DBC,即∠ABD=∠CBE. ∴∠CBE= 12(∠ABE-∠DBC)= 12×(160°-30°)=65°.
(2)∵△ABC≌△DBE,∴BE=BC=4.5cm,DE=AC=AD+DC=6cm.
∴△DCP与△BPE的周长之和为
DC+DP+PC+BP+PE+BE=(DP+PE)+(BP+PC)+DC+BE=DE+BC+DC+BE=6+4.5+3+4.5=18(cm).
