2021-2022学年人教版数学八年级上册 12.2 三角形全等的判定(一) 同步练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册 12.2 三角形全等的判定(一) 同步练习 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 151.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 16:36:27 | ||
图片预览


文档简介
1268730010502900第十二章 全等三角形
12.2 三角形全等的判定(一)
课堂笔记
1. 判定方法一:三边对应 的两个三角形全等(可以简写成“边边边”或“SSS”).
2. 书写格式:
(1)先写出所要判定的两个三角形;
(2)列出条件:用大括号将两个三角形中相等的边分别写出;
(3)得出结论:两个三角形全等.
分层训练
A组 基础训练
1. 如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定( )
A. △ABD≌△ACD B. △ABE≌△ACE
C. △BDE≌△CDE D. 以上答案都不对
2. 如图,在△ABC和△DCB中,AB=DC,AC与BD相交于点E,若不再添加任何字母与辅助线,要使△ABC≌△DCB,则还需增加的一个条件是( )
A. AC=BD B. AC=BC
C. BE=CE D. AE=DE
3. 如图,已知AB=AC,BD=DC,那么下列结论中不正确的是( )
A. △ABD≌△ACD
B. ∠ADB=90°
C. ∠BAD是∠B的一半
D. AD平分∠BAC
4. 如果△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x-1,若△ABC≌△DEF,则x等于( )
A. 73 B. 3 C. 4 D. 5
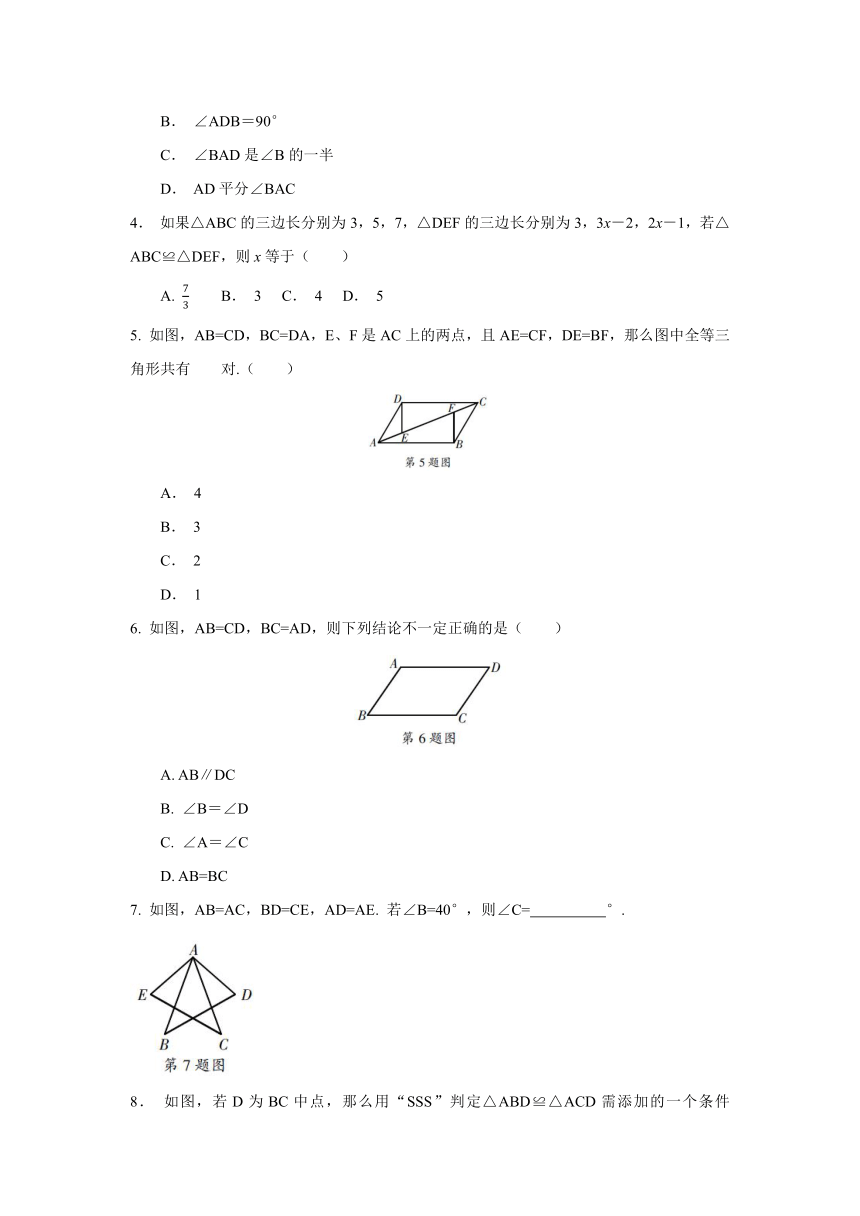
5. 如图,AB=CD,BC=DA,E、F是AC上的两点,且AE=CF,DE=BF,那么图中全等三角形共有 对.( )
A. 4
B. 3
C. 2
D. 1
6. 如图,AB=CD,BC=AD,则下列结论不一定正确的是( )
A. AB∥DC
B. ∠B=∠D
C. ∠A=∠C
D. AB=BC
7. 如图,AB=AC,BD=CE,AD=AE. 若∠B=40°,则∠C= °.
8. 如图,若D为BC中点,那么用“SSS”判定△ABD≌△ACD需添加的一个条件是 .
9. 如图,用直尺和圆规作一个角等于已知角,能得出∠A′O′B′=∠AOB的依据是 .
10. 如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF. 请证明下列结论:
(1)∠D=∠B;
(2)AE∥CF.
B组 自主提高
11. (厦门中考)如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F. 若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
A. ∠EDB
B. ∠BED
C. 12 ∠AFB
D. 2∠ABF
12. 工人师傅常用角尺平分一个任意角. 作法如下:
如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C作射线OC. 由作法得△MOC≌△NOC的依据是 .
13. 在如图所示的6×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),则与△ABC有一条公共边BC且全等的所有格点三角形的个数是 个.
14. 如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
15. 如图,已知AB=AC,AD=AE,BD=CE,求证:∠3=∠1+∠2.
16. 如图,已知AB=CD,AD=CB,求证:
(1)AB∥DC;
(2)∠APC=∠DCP.
C组 综合运用
17. 如图,已知AB=CD,AC=BD,求证:∠A=∠D.
参考答案
【课堂笔记】
1. 相等
【分层训练】
1—5. BACBB 6. D
7. 40
8. AB=AC
9. SSS
10. (1)由“SSS”证△AED≌△CFB即可得.
(2)由(1)知,△AED≌△CFB,∴∠AED=∠CFB,∴∠AEO=∠CFO,∴AE∥CF.
11. C
12. SSS
13. 3
14. (1)证明:∵BF=CE,∴BF+FC=CE+FC,即BC=EF,
在△ABC和△DEF中,BC=EF,AB=DE,AC=DF,∴△ABC≌△DEF(SSS);
(2)由(1)知△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE,∴AB∥DE,AC∥DF.
15. 证明:在△ABD和△ACE中,AB=AC,AD=AE,BD=CE,
∴△ABD≌△ACE(SSS),∴∠BAD=∠1,∠ABD=∠2,
∵∠3是△ABD的外角,∴∠3=∠BAD+∠ABD=∠1+∠2.
16. 证明:
(1)连接AC,在△ABC和△CDA中,AB=CD(已知),CB=AD(已知),AC=CA(公共边),∴ △ABC≌△CDA(SSS),∴∠BAC=∠DCA. ∴AB∥DC.
(2)由(1)知:BP∥DC,∴∠APC=∠DCP.
17. 连接BC,∵在△BCD和△CBA中,AB=DC,AC=DB,BC=CB,∴△BAC≌△CDB(SSS),∴∠A=∠D.
12.2 三角形全等的判定(一)
课堂笔记
1. 判定方法一:三边对应 的两个三角形全等(可以简写成“边边边”或“SSS”).
2. 书写格式:
(1)先写出所要判定的两个三角形;
(2)列出条件:用大括号将两个三角形中相等的边分别写出;
(3)得出结论:两个三角形全等.
分层训练
A组 基础训练
1. 如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定( )
A. △ABD≌△ACD B. △ABE≌△ACE
C. △BDE≌△CDE D. 以上答案都不对
2. 如图,在△ABC和△DCB中,AB=DC,AC与BD相交于点E,若不再添加任何字母与辅助线,要使△ABC≌△DCB,则还需增加的一个条件是( )
A. AC=BD B. AC=BC
C. BE=CE D. AE=DE
3. 如图,已知AB=AC,BD=DC,那么下列结论中不正确的是( )
A. △ABD≌△ACD
B. ∠ADB=90°
C. ∠BAD是∠B的一半
D. AD平分∠BAC
4. 如果△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x-1,若△ABC≌△DEF,则x等于( )
A. 73 B. 3 C. 4 D. 5
5. 如图,AB=CD,BC=DA,E、F是AC上的两点,且AE=CF,DE=BF,那么图中全等三角形共有 对.( )
A. 4
B. 3
C. 2
D. 1
6. 如图,AB=CD,BC=AD,则下列结论不一定正确的是( )
A. AB∥DC
B. ∠B=∠D
C. ∠A=∠C
D. AB=BC
7. 如图,AB=AC,BD=CE,AD=AE. 若∠B=40°,则∠C= °.
8. 如图,若D为BC中点,那么用“SSS”判定△ABD≌△ACD需添加的一个条件是 .
9. 如图,用直尺和圆规作一个角等于已知角,能得出∠A′O′B′=∠AOB的依据是 .
10. 如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF. 请证明下列结论:
(1)∠D=∠B;
(2)AE∥CF.
B组 自主提高
11. (厦门中考)如图,在△ABC和△BDE中,点C在边BD上,边AC交边BE于点F. 若AC=BD,AB=ED,BC=BE,则∠ACB等于( )
A. ∠EDB
B. ∠BED
C. 12 ∠AFB
D. 2∠ABF
12. 工人师傅常用角尺平分一个任意角. 作法如下:
如图,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C作射线OC. 由作法得△MOC≌△NOC的依据是 .
13. 在如图所示的6×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),则与△ABC有一条公共边BC且全等的所有格点三角形的个数是 个.
14. 如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
15. 如图,已知AB=AC,AD=AE,BD=CE,求证:∠3=∠1+∠2.
16. 如图,已知AB=CD,AD=CB,求证:
(1)AB∥DC;
(2)∠APC=∠DCP.
C组 综合运用
17. 如图,已知AB=CD,AC=BD,求证:∠A=∠D.
参考答案
【课堂笔记】
1. 相等
【分层训练】
1—5. BACBB 6. D
7. 40
8. AB=AC
9. SSS
10. (1)由“SSS”证△AED≌△CFB即可得.
(2)由(1)知,△AED≌△CFB,∴∠AED=∠CFB,∴∠AEO=∠CFO,∴AE∥CF.
11. C
12. SSS
13. 3
14. (1)证明:∵BF=CE,∴BF+FC=CE+FC,即BC=EF,
在△ABC和△DEF中,BC=EF,AB=DE,AC=DF,∴△ABC≌△DEF(SSS);
(2)由(1)知△ABC≌△DEF,
∴∠ABC=∠DEF,∠ACB=∠DFE,∴AB∥DE,AC∥DF.
15. 证明:在△ABD和△ACE中,AB=AC,AD=AE,BD=CE,
∴△ABD≌△ACE(SSS),∴∠BAD=∠1,∠ABD=∠2,
∵∠3是△ABD的外角,∴∠3=∠BAD+∠ABD=∠1+∠2.
16. 证明:
(1)连接AC,在△ABC和△CDA中,AB=CD(已知),CB=AD(已知),AC=CA(公共边),∴ △ABC≌△CDA(SSS),∴∠BAC=∠DCA. ∴AB∥DC.
(2)由(1)知:BP∥DC,∴∠APC=∠DCP.
17. 连接BC,∵在△BCD和△CBA中,AB=DC,AC=DB,BC=CB,∴△BAC≌△CDB(SSS),∴∠A=∠D.
