24.2 点和圆、直线和圆的位置关系 人教版九年级数学上册 同步课时训练(word版含答案)
文档属性
| 名称 | 24.2 点和圆、直线和圆的位置关系 人教版九年级数学上册 同步课时训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 459.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 17:28:16 | ||
图片预览




文档简介
24.2 点和圆、直线和圆的位置关系 人教版九年级数学上册 同步课时训练
一、选择题
1. 在数轴上,点A所表示的实数为5,点B所表示的实数为a,⊙A的半径为3,要使点B在⊙A内,则实数a的取值范围是( )
A.a>2 B.a>8
C.2<a<8 D.a<2或a>8
2. 如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( )
A.DE=DO B.AB=AC
C.CD=DB D.AC∥OD
3. 如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与图中7×4方格中的格点相连,连线能够与该圆弧相切的格点有( )
A.1个 B.2个
C.3个 D.4个
4. 已知⊙O的面积为9π cm2,若点O到直线l的距离为π cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切
C.相离 D.无法确定
5. 已知:在△ABC中,AB=AC,求证:∠B<90°.下面写出了用反证法证明这个命题过程中的四个推理步骤:①因为∠B+∠C≥180°与三角形内角和定理相矛盾;②所以∠B<90°;③假设∠B≥90°;④由AB=AC,得∠C=∠B≥90°,即∠B+∠C≥180°.这四个步骤正确的顺序应是( )
A.①②③④ B.③④②①
C.③④①② D.④③②①
6. 如图,⊙O的半径为2,点O到直线l的距离为3,P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
A. B. C.3 D.2
7. 如图,⊙C的半径为1,圆心的坐标为(3,4),P(m,n)是⊙C内或⊙C上的一个动点,则m2+n2的最小值是( )
A.9 B.16 C.25 D.36
8. 如图,在网格中(每个小正方形的边长均为1个单位长度)选取9个格点(格线的交点称为格点).如果以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
图
A.2<r≤ B.<r≤3
C.<r≤5 D.5<r≤
二、填空题
9. 直角三角形的两条直角边分别是5和12,则它的内切圆半径为 .?
10. 如图,⊙M的圆心在一次函数y=x+2的图象上运动,半径为1.当⊙M与y轴相切时,点M的坐标为__________.
11. 如图1,已知△ABC的外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向三角形外作等腰直角三角形ABD与ACE,连接BE,CD交于点P,则OP长的最小值是________.
12. 如图,在矩形ABCD中,AB=6,BC=2.8,⊙O是以AB为直径的圆,则直线CD与⊙O的位置关系是________.
13. 如图,在△ABC中,∠A=60°,BC=5 cm.能够将△ABC完全覆盖的最小圆形纸片的直径是________cm.
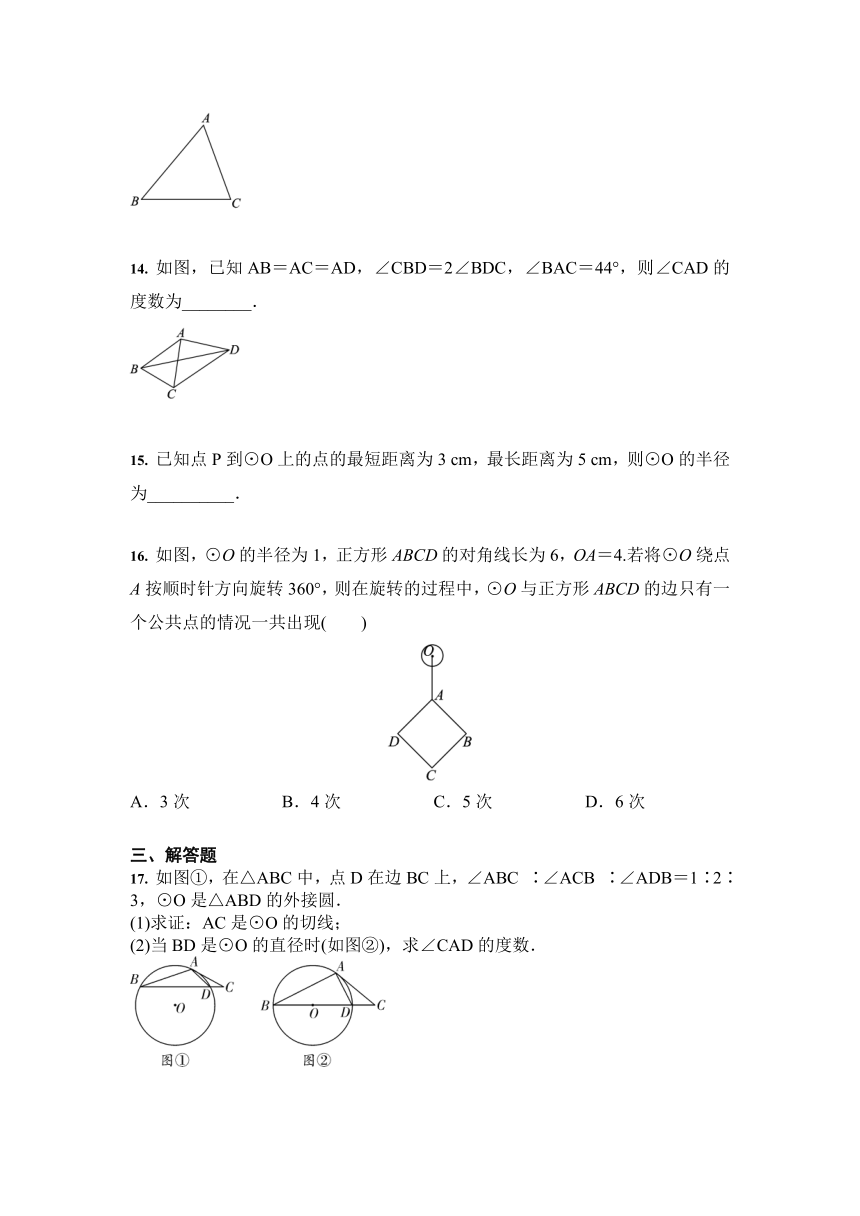
14. 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为________.
15. 已知点P到⊙O上的点的最短距离为3 cm,最长距离为5 cm,则⊙O的半径为__________.
16. 如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,则在旋转的过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )
A.3次 B.4次 C.5次 D.6次
三、解答题
17. 如图①,在△ABC中,点D在边BC上,∠ABC ∶∠ACB ∶∠ADB=1∶2∶3,⊙O是△ABD的外接圆.
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图②),求∠CAD的度数.
18. 2018·邵阳 如图所示,AB是⊙O的直径,C为⊙O上一点,过点B作BD⊥CD,垂足为D,连接BC,BC平分∠ABD.
求证:CD为⊙O的切线.
19. 如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF,DC.已知OA=OB,CA=CB.
(1)求证:直线AB是⊙O的切线;
(2)求证:∠CDF=∠EDC;
(3)若DE=10,DF=8,求CD的长.
24.2 点和圆、直线和圆的位置关系 人教版九年级数学上册 同步课时训练-答案
一、选择题
1. 【答案】C
2. 【答案】A
3. 【答案】C [解析] 如图,连接AB,BC,作AB,BC的垂直平分线,可得点A,B,C所在的圆的圆心为O′(2,0).
只有当∠O′BF=∠O′BD+∠DBF=90°时,BF与圆相切,
此时△BO′D≌△FBE,EF=DB=2,
此时点F的坐标为(5,1).
作过点B,F的直线,直线BF经过格点(1,3),(7,0),此两点亦符合要求.
即与点B的连线,能够与该圆弧相切的格点是(5,1)或(1,3)或(7,0),共3个.
4. 【答案】C [解析] 由题意可知,圆的半径为3 cm.∵圆心到直线l的距离为π cm>圆的半径3 cm,∴直线l与⊙O相离.故选C.
5. 【答案】C
6. 【答案】B [解析] ∵PQ与⊙O相切,∴∠OQP=90°,∴PQ==,∴当OP最小时,PQ最小.而OP的最小值是点O到直线l的距离3,∴PQ的最小值为=.故选B.
7. 【答案】B [解析] 如图,连接OC交⊙C于点P′.
∵圆心C的坐标为(3,4),点P的坐标为(m,n),
∴OC=5,OP=,
∴m2+n2是点P到原点的距离的平方,
∴当点P运动到线段OC上,即点P′处时,点P离原点最近,即m2+n2取得最小值,
此时OP=OC-PC=5-1=4,即m2+n2=16.
8. 【答案】B [解析] 如图,∵AD=2 ,AE=AF=,AB=3 ,
∴AB>AE=AF>AD,
∴当<r<3 时,以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.
二、填空题
9. 【答案】2 [解析]直角三角形的斜边==13,所以它的内切圆半径==2.
10. 【答案】(1,)或(-1,) [解析] ∵⊙M的圆心在一次函数y=x+2的图象上运动,∴设当⊙M与y轴相切时圆心M的坐标为(x,x+2).∵⊙M的半径为1,∴x=1或x=-1,当x=1时,y=,当x=-1时,y=.∴点M的坐标为(1,)或(-1,).
11. 【答案】5- [解析] ∵∠BAD=∠CAE=90°,
∴∠DAC=∠BAE.
在△DAC和△BAE中,
∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE,
从而∠PDB+∠PBD=90°,
即∠DPB=90°,从而∠BPC=90°,
∴点P在以BC为直径的圆上.
如图,过点O作OH⊥BC于点H,连接OB,OC.
∵△ABC的外心为O,∠BAC=60°,
∴∠BOC=120°.又∵BC=10,
∴OH= ,∴OP长的最小值是5- .
12. 【答案】相交 [解析] 设AB的中点为O,则点O到CD的距离为2.8.因为⊙O的半径为3,3>2.8,所以直线CD与⊙O的位置关系是相交.
13. 【答案】 如图,能够将△ABC完全覆盖的最小圆形纸片是△ABC的外接圆⊙O.连接OB,OC,则∠BOC=2∠A=120°.过点O作OD⊥BC于点D,则∠BOD=∠BOC=60°.∴∠OBD=30°,
∴OB=2OD.由垂径定理,得BD=BC= cm,在Rt△BOD中,由勾股定理,得OB2=OD2+BD2,即(2OD)2=OD2+()2,解得OD= cm.∴OB= cm,∴能够将△ABC完全覆盖的最小圆形纸片的直径是 cm.
14. 【答案】 [解析] ∵AB=AC=AD,
∴点A是△BCD的外心,
∴∠BAC=2∠BDC.
∵∠CBD=2∠BDC,
∴∠CBD=∠BAC=44°,
∴∠CAD=2∠CBD=88°.
15. 【答案】1 cm或4 cm [解析] 若点P在⊙O内,如图①.∵AP=3 cm,BP=5 cm,
∴AB=8 cm,∴OA=4 cm;
若点P在⊙O外,如图②.
∵AP=3 cm,BP=5 cm,
∴AB=2 cm,
∴OA=1 cm.
16. 【答案】B [解析] ∵正方形ABCD的对角线长为6,∴它的边长为3 .
如图,⊙O与正方形ABCD的边AB,AD只有一个公共点的情况各有1次,与边BC,CD只有一个公共点的情况各有1次,
∴在旋转的过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现4次.
三、解答题
17. 【答案】
(1)证明:如解图,连接OA,OD.设∠ABC=x,
∵∠ABC∶∠ACB∶∠ADB=1∶2∶3,
∴∠ADB=3x,∠ACB=2x,
解图
∴ ∠DAC=x,∠AOD=2∠ABC=2x,
∴∠OAD==90°-x,(2分)
∴∠OAC=90°-x+x=90°,
∴OA⊥AC,
又∵OA为⊙O的半径,
∴AC是⊙O的切线.(4分)
(2)解:∵BD是⊙O的直径,
∴∠BAD=90°,
∵∠ABC∶∠ACB∶∠ADB=1∶2∶3,
∠ABC+∠ADB=90°,
∴∠ABC+3∠ABC=90°,(6分)
解得∠ABC=22.5°,
∴∠ADB=67.5°,∠ACB=45°,
∴∠CAD=∠ADB-∠ACB=22.5°.(8分)
18. 【答案】
证明:连接OC.∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,∴OC⊥CD,∴CD为⊙O的切线.
19. 【答案】
解:(1)证明:如图,连接OC.
∵OA=OB,AC=CB,
∴OC⊥AB.
又∵点C在⊙O上,
∴直线AB是⊙O的切线.
(2)证明:∵OA=OB,AC=CB,
∴∠AOC=∠BOC.
∵OD=OF,
∴∠ODF=∠OFD.
∵∠AOB=∠ODF+∠OFD=∠AOC+∠BOC,
∴∠BOC=∠OFD,
∴OC∥DF,
∴∠CDF=∠OCD.
∵OD=OC,
∴∠ODC=∠OCD,
∴∠CDF=∠EDC.
(3)如图,过点O作ON⊥DF于点N,延长DF交AB于点M.
∵ON⊥DF,
∴DN=NF=4.
在Rt△ODN中,∵∠OND=90°,OD=5,DN=4,
∴ON==3.
由(2)知OC∥DF,
∴∠OCM+∠CMN=180°.
由(1)知∠OCM=90°,
∴∠CMN=90°=∠OCM=∠MNO,
∴四边形OCMN是矩形,
∴CM=ON=3,MN=OC=5.
在Rt△CDM中,∵∠DMC=90°,CM=3,DM=DN+MN=9,
∴CD===3.
一、选择题
1. 在数轴上,点A所表示的实数为5,点B所表示的实数为a,⊙A的半径为3,要使点B在⊙A内,则实数a的取值范围是( )
A.a>2 B.a>8
C.2<a<8 D.a<2或a>8
2. 如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,要使DE是⊙O的切线,还需补充一个条件,则补充的条件不正确的是( )
A.DE=DO B.AB=AC
C.CD=DB D.AC∥OD
3. 如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与图中7×4方格中的格点相连,连线能够与该圆弧相切的格点有( )
A.1个 B.2个
C.3个 D.4个
4. 已知⊙O的面积为9π cm2,若点O到直线l的距离为π cm,则直线l与⊙O的位置关系是( )
A.相交 B.相切
C.相离 D.无法确定
5. 已知:在△ABC中,AB=AC,求证:∠B<90°.下面写出了用反证法证明这个命题过程中的四个推理步骤:①因为∠B+∠C≥180°与三角形内角和定理相矛盾;②所以∠B<90°;③假设∠B≥90°;④由AB=AC,得∠C=∠B≥90°,即∠B+∠C≥180°.这四个步骤正确的顺序应是( )
A.①②③④ B.③④②①
C.③④①② D.④③②①
6. 如图,⊙O的半径为2,点O到直线l的距离为3,P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为( )
A. B. C.3 D.2
7. 如图,⊙C的半径为1,圆心的坐标为(3,4),P(m,n)是⊙C内或⊙C上的一个动点,则m2+n2的最小值是( )
A.9 B.16 C.25 D.36
8. 如图,在网格中(每个小正方形的边长均为1个单位长度)选取9个格点(格线的交点称为格点).如果以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
图
A.2<r≤ B.<r≤3
C.<r≤5 D.5<r≤
二、填空题
9. 直角三角形的两条直角边分别是5和12,则它的内切圆半径为 .?
10. 如图,⊙M的圆心在一次函数y=x+2的图象上运动,半径为1.当⊙M与y轴相切时,点M的坐标为__________.
11. 如图1,已知△ABC的外心为O,BC=10,∠BAC=60°,分别以AB,AC为腰向三角形外作等腰直角三角形ABD与ACE,连接BE,CD交于点P,则OP长的最小值是________.
12. 如图,在矩形ABCD中,AB=6,BC=2.8,⊙O是以AB为直径的圆,则直线CD与⊙O的位置关系是________.
13. 如图,在△ABC中,∠A=60°,BC=5 cm.能够将△ABC完全覆盖的最小圆形纸片的直径是________cm.
14. 如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为________.
15. 已知点P到⊙O上的点的最短距离为3 cm,最长距离为5 cm,则⊙O的半径为__________.
16. 如图,⊙O的半径为1,正方形ABCD的对角线长为6,OA=4.若将⊙O绕点A按顺时针方向旋转360°,则在旋转的过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现( )
A.3次 B.4次 C.5次 D.6次
三、解答题
17. 如图①,在△ABC中,点D在边BC上,∠ABC ∶∠ACB ∶∠ADB=1∶2∶3,⊙O是△ABD的外接圆.
(1)求证:AC是⊙O的切线;
(2)当BD是⊙O的直径时(如图②),求∠CAD的度数.
18. 2018·邵阳 如图所示,AB是⊙O的直径,C为⊙O上一点,过点B作BD⊥CD,垂足为D,连接BC,BC平分∠ABD.
求证:CD为⊙O的切线.
19. 如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF,DC.已知OA=OB,CA=CB.
(1)求证:直线AB是⊙O的切线;
(2)求证:∠CDF=∠EDC;
(3)若DE=10,DF=8,求CD的长.
24.2 点和圆、直线和圆的位置关系 人教版九年级数学上册 同步课时训练-答案
一、选择题
1. 【答案】C
2. 【答案】A
3. 【答案】C [解析] 如图,连接AB,BC,作AB,BC的垂直平分线,可得点A,B,C所在的圆的圆心为O′(2,0).
只有当∠O′BF=∠O′BD+∠DBF=90°时,BF与圆相切,
此时△BO′D≌△FBE,EF=DB=2,
此时点F的坐标为(5,1).
作过点B,F的直线,直线BF经过格点(1,3),(7,0),此两点亦符合要求.
即与点B的连线,能够与该圆弧相切的格点是(5,1)或(1,3)或(7,0),共3个.
4. 【答案】C [解析] 由题意可知,圆的半径为3 cm.∵圆心到直线l的距离为π cm>圆的半径3 cm,∴直线l与⊙O相离.故选C.
5. 【答案】C
6. 【答案】B [解析] ∵PQ与⊙O相切,∴∠OQP=90°,∴PQ==,∴当OP最小时,PQ最小.而OP的最小值是点O到直线l的距离3,∴PQ的最小值为=.故选B.
7. 【答案】B [解析] 如图,连接OC交⊙C于点P′.
∵圆心C的坐标为(3,4),点P的坐标为(m,n),
∴OC=5,OP=,
∴m2+n2是点P到原点的距离的平方,
∴当点P运动到线段OC上,即点P′处时,点P离原点最近,即m2+n2取得最小值,
此时OP=OC-PC=5-1=4,即m2+n2=16.
8. 【答案】B [解析] 如图,∵AD=2 ,AE=AF=,AB=3 ,
∴AB>AE=AF>AD,
∴当<r<3 时,以点A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内.
二、填空题
9. 【答案】2 [解析]直角三角形的斜边==13,所以它的内切圆半径==2.
10. 【答案】(1,)或(-1,) [解析] ∵⊙M的圆心在一次函数y=x+2的图象上运动,∴设当⊙M与y轴相切时圆心M的坐标为(x,x+2).∵⊙M的半径为1,∴x=1或x=-1,当x=1时,y=,当x=-1时,y=.∴点M的坐标为(1,)或(-1,).
11. 【答案】5- [解析] ∵∠BAD=∠CAE=90°,
∴∠DAC=∠BAE.
在△DAC和△BAE中,
∴△DAC≌△BAE(SAS),
∴∠ADC=∠ABE,
从而∠PDB+∠PBD=90°,
即∠DPB=90°,从而∠BPC=90°,
∴点P在以BC为直径的圆上.
如图,过点O作OH⊥BC于点H,连接OB,OC.
∵△ABC的外心为O,∠BAC=60°,
∴∠BOC=120°.又∵BC=10,
∴OH= ,∴OP长的最小值是5- .
12. 【答案】相交 [解析] 设AB的中点为O,则点O到CD的距离为2.8.因为⊙O的半径为3,3>2.8,所以直线CD与⊙O的位置关系是相交.
13. 【答案】 如图,能够将△ABC完全覆盖的最小圆形纸片是△ABC的外接圆⊙O.连接OB,OC,则∠BOC=2∠A=120°.过点O作OD⊥BC于点D,则∠BOD=∠BOC=60°.∴∠OBD=30°,
∴OB=2OD.由垂径定理,得BD=BC= cm,在Rt△BOD中,由勾股定理,得OB2=OD2+BD2,即(2OD)2=OD2+()2,解得OD= cm.∴OB= cm,∴能够将△ABC完全覆盖的最小圆形纸片的直径是 cm.
14. 【答案】 [解析] ∵AB=AC=AD,
∴点A是△BCD的外心,
∴∠BAC=2∠BDC.
∵∠CBD=2∠BDC,
∴∠CBD=∠BAC=44°,
∴∠CAD=2∠CBD=88°.
15. 【答案】1 cm或4 cm [解析] 若点P在⊙O内,如图①.∵AP=3 cm,BP=5 cm,
∴AB=8 cm,∴OA=4 cm;
若点P在⊙O外,如图②.
∵AP=3 cm,BP=5 cm,
∴AB=2 cm,
∴OA=1 cm.
16. 【答案】B [解析] ∵正方形ABCD的对角线长为6,∴它的边长为3 .
如图,⊙O与正方形ABCD的边AB,AD只有一个公共点的情况各有1次,与边BC,CD只有一个公共点的情况各有1次,
∴在旋转的过程中,⊙O与正方形ABCD的边只有一个公共点的情况一共出现4次.
三、解答题
17. 【答案】
(1)证明:如解图,连接OA,OD.设∠ABC=x,
∵∠ABC∶∠ACB∶∠ADB=1∶2∶3,
∴∠ADB=3x,∠ACB=2x,
解图
∴ ∠DAC=x,∠AOD=2∠ABC=2x,
∴∠OAD==90°-x,(2分)
∴∠OAC=90°-x+x=90°,
∴OA⊥AC,
又∵OA为⊙O的半径,
∴AC是⊙O的切线.(4分)
(2)解:∵BD是⊙O的直径,
∴∠BAD=90°,
∵∠ABC∶∠ACB∶∠ADB=1∶2∶3,
∠ABC+∠ADB=90°,
∴∠ABC+3∠ABC=90°,(6分)
解得∠ABC=22.5°,
∴∠ADB=67.5°,∠ACB=45°,
∴∠CAD=∠ADB-∠ACB=22.5°.(8分)
18. 【答案】
证明:连接OC.∵BC平分∠ABD,
∴∠OBC=∠DBC.
∵OB=OC,∴∠OBC=∠OCB,
∴∠OCB=∠DBC,
∴OC∥BD.
∵BD⊥CD,∴OC⊥CD,∴CD为⊙O的切线.
19. 【答案】
解:(1)证明:如图,连接OC.
∵OA=OB,AC=CB,
∴OC⊥AB.
又∵点C在⊙O上,
∴直线AB是⊙O的切线.
(2)证明:∵OA=OB,AC=CB,
∴∠AOC=∠BOC.
∵OD=OF,
∴∠ODF=∠OFD.
∵∠AOB=∠ODF+∠OFD=∠AOC+∠BOC,
∴∠BOC=∠OFD,
∴OC∥DF,
∴∠CDF=∠OCD.
∵OD=OC,
∴∠ODC=∠OCD,
∴∠CDF=∠EDC.
(3)如图,过点O作ON⊥DF于点N,延长DF交AB于点M.
∵ON⊥DF,
∴DN=NF=4.
在Rt△ODN中,∵∠OND=90°,OD=5,DN=4,
∴ON==3.
由(2)知OC∥DF,
∴∠OCM+∠CMN=180°.
由(1)知∠OCM=90°,
∴∠CMN=90°=∠OCM=∠MNO,
∴四边形OCMN是矩形,
∴CM=ON=3,MN=OC=5.
在Rt△CDM中,∵∠DMC=90°,CM=3,DM=DN+MN=9,
∴CD===3.
同课章节目录
