2021-2022学年八年级数学人教版上册 11.2.2三角形的外角同步随堂练习题 (word版含解析)
文档属性
| 名称 | 2021-2022学年八年级数学人教版上册 11.2.2三角形的外角同步随堂练习题 (word版含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 122.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 17:32:09 | ||
图片预览
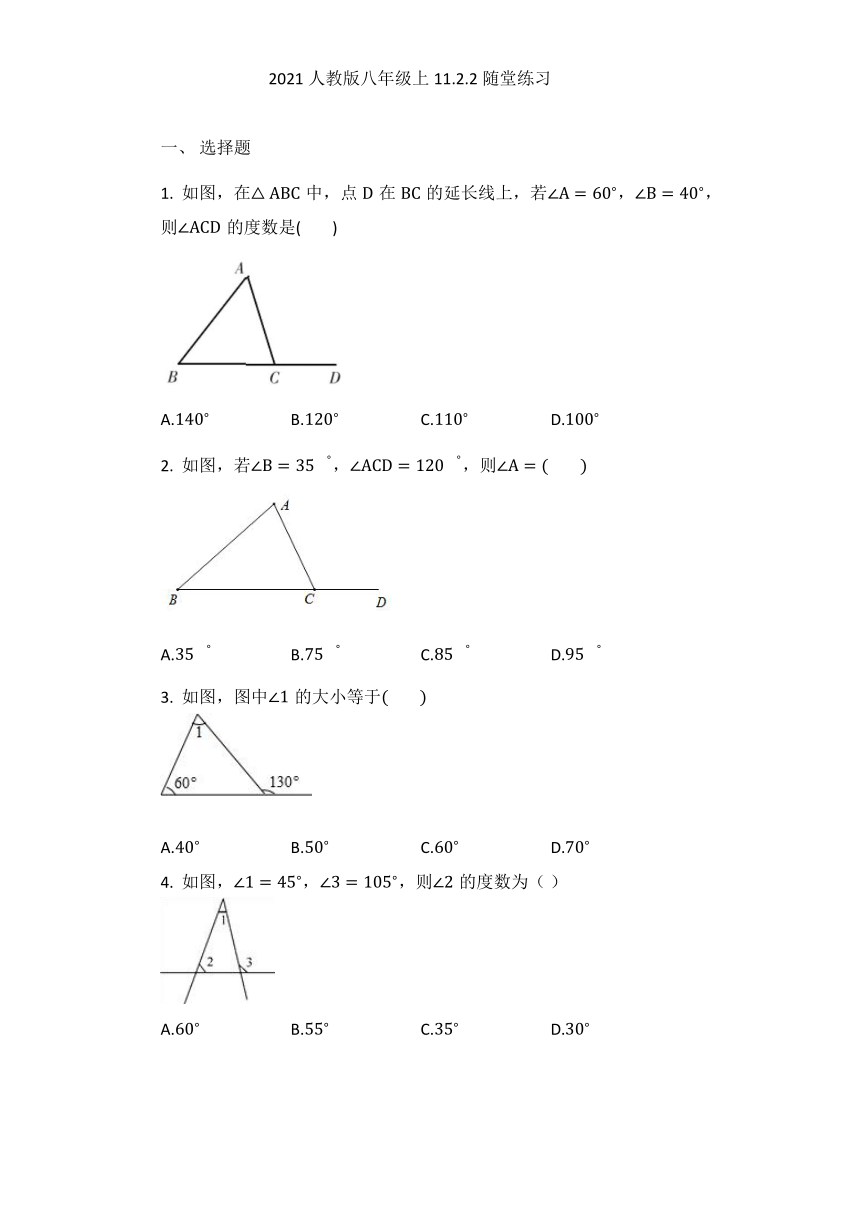


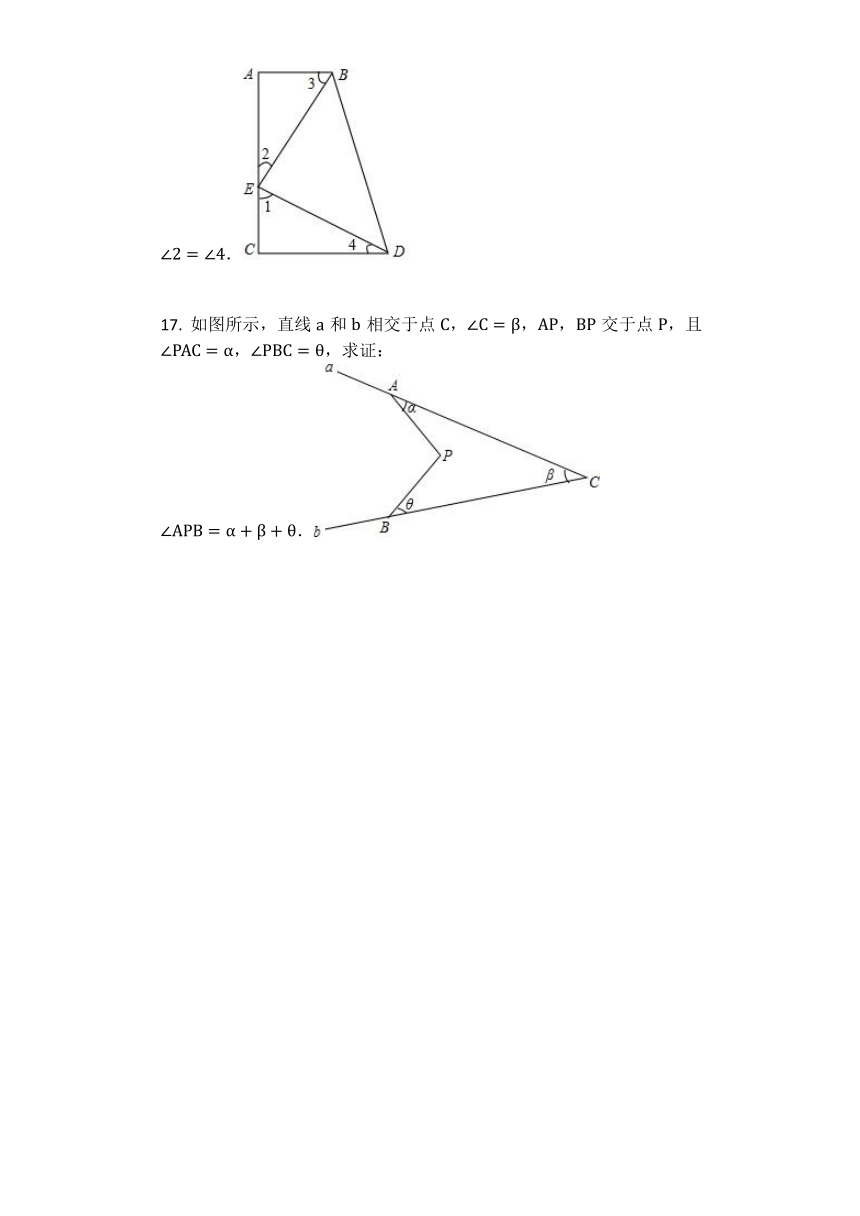

文档简介
2021人教版八年级上11.2.2随堂练习
一、 选择题
1. 如图,在△ABC中,点D在BC的延长线上,若∠A=60?,∠B=40?,则∠ACD的度数是(? ? ? ? )
A.140? B.120? C.110? D.100?
2. 如图,若∠B=35??,∠ACD=120??,则∠A=(? ? ? ? )
A.35?? B.75?? C.85?? D.95??
3. 如图,图中∠1的大小等于(? ? ? ? )?
A.40? B.50? C.60? D.70?
4. 如图,∠1=45?,∠3=105?,则∠2的度数为( )
A.60? B.55? C.35? D.30?
5. 如图,∠A,∠DOE,∠BEC的大小关系是( )
A.∠A>∠DOE>∠BEC B.∠DOE>∠BEC>∠A
C.∠DOE>∠A>∠BEC D.∠BEC>∠DOE>∠A
6. 如图,在△ABC中,∠ACB=90?,沿CD折叠△CBD,使点B恰好落在边AC上点E处,若∠A=25?,则∠ADE的大小为( )
A.40? B.50? C.65? D.75?
7. 如图,在△ABC中,∠ACB=90?,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=20?,则∠BDC的度数为( )
A.70? B.65? C.60? D.40?
8. 已知△ABC的外角∠CBE,∠BCF的角平分线BP,CP交于P点,则∠BPC是( )
A.钝角 B.锐角 C.直角 D.无法确定
9. 如图所示,一副三角板放在两条平行线MN,PQ之间,含30?角的三角板的较长直角边在直线PQ上,含45?角的三角板的一条直角边在另一个三角板的斜边上,则∠NAC的度数是(? ? ? ? )
A.100? B.108? C.110? D.120?
10. 如图,将纸片△ABC沿着DE折叠,若∠1+∠2=60?,则∠A的大小为( )
A.20? B.25? C.30? D.35?
二、 填空题 ?
11. △ABC中,∠B=∠A+10?,∠C=∠B+10?,则∠A=________??.
12. 在直角三角形中,两个锐角的度数比为2:3,那么较小锐角的度数是________.
13. 如图,在四边形ABCD中,∠A与∠DCB互补,E为BC延长线上的点,且∠1+∠2+∠DCE=224?,则∠A的度数是________.
14. 如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB,∠A=100?,则∠BOC=________度.
三、 解答题 ?
15. 如图,在△ABC中,∠ACB=90?,CD是△ABC的一条高线,若∠B=28?.求∠ACD的度数.
?
16. 如图,∠A=∠C=∠BED=90?,求证:∠1=∠3,∠2=∠4.
?
17. 如图所示,直线a和b相交于点C,∠C=β,AP,BP交于点P,且∠PAC=α,∠PBC=θ,求证:∠APB=α+β+θ.
参考答案与试题解析
一、 选择题
1.
【答案】
D
【解答】
解:∵ ∠ACD是△ABC的一个外角,
∴ ∠ACD=∠A+∠B,
∵ ∠A=60?,∠B=40?,
∴ ∠ACD=60?+40?=100?.
故选D.
2.
【答案】
C
【解答】
解:由题意可得:?∠A=∠ACD?∠B=120??35?=85?.
故选C.
3.
【答案】
D
【解答】
解:由三角形的外角性质得,∠1=130??60?=70?.
故选D.
4.
【答案】
A
【解答】
此题暂无解答
5.
【答案】
B
【解答】
解:∵ ∠BEC是△ABE的外角,
∴ ∠BEC>∠A,
∵ ∠DOE是△COE的外角,
∴ ∠DOE>∠BEC,
∴ ∠DOE>∠BEC>∠A,
故选:B.
6.
【答案】
A
【解答】
∵ 在△ABC中,∠ACB=90?,∠A=25?,
∴ ∠B=180??90??25?=65?,
根据折叠可得∠CED=65?,
∴ ∠ADE=65??25?=40?,
7.
【答案】
B
【解答】
此题暂无解答
8.
【答案】
B
【解答】
解:∵ △ABC的外角平分线BP,CP交于P点,
∴ ∠PBC=12∠EBC,∠BCP=12∠BCF,
∵ ∠CBE、∠BCF是△ABC的两个外角,
∴ ∠CBE+∠BCF=360??(180??∠A)=180?+∠A,
∴ ∠PBC+∠BCP=12(∠EBC+∠BCF)=12(180?+∠A)=90?+12∠A,
∵ 在△PBC中,∠BPC=180??(∠PBC+∠BCP)=180??(90?+12∠A)=90??12∠A<90?,
∴ ∠BPC是锐角.
故选:B.
9.
【答案】
D
【解答】
解:延长AC交PQ于点G,则∠GCB=90?,
∴ ∠AGQ=60?.
∵ PQ//MN,
∴ ∠NAC+∠AGQ=180?,
∴ ∠NAC=180??60?=120?.
故选D.
10.
【答案】
C
【解答】
根据折叠及邻补角的性质,得
∠1=180??2∠ADE,∠2=180??2∠AED,
∴ ∠1+∠2=360??2(∠ADE+∠AED),
∵ ∠1+∠2=60?
∴ ∠ADE+∠AED=150?,
∴ 在△ADE中,由内角和定理,得
∠A=180??(∠ADE+∠AED)=30?,
二、 填空题
11.
【答案】
50?
【解答】
此题暂无解答
12.
【答案】
36?
【解答】
解:设两锐角分别为2k、3k,由题意得
2k+3k=90?
解得k=18?
所以较小锐角的度数为18×2=36?
故答案为:36?.
13.
【答案】
[加加)112?
【解答】
此题暂无解答
14.
【答案】
140
【解答】
此题暂无解答
三、 解答题
15.
【答案】
解:∵ ∠ACB=90?,
∴ ∠ACD+∠BCD=90?,
∵ CD是△ABC的一条高线,
∴ ∠B+∠BCD=90?,
∴ ∠ACD=∠B=28?.
【解答】
解:∵ ∠ACB=90?,
∴ ∠ACD+∠BCD=90?,
∵ CD是△ABC的一条高线,
∴ ∠B+∠BCD=90?,
∴ ∠ACD=∠B=28?.
16.
【答案】
证明:∵ ∠BED=90?,
∴ ∠1+∠2=180??90?=90?,
∵ ∠A=90?,
∴ ∠2+∠3=90?,
∴ ∠1=∠3;
同理可得∠2=∠4.
【解答】
证明:∵ ∠BED=90?,
∴ ∠1+∠2=180??90?=90?,
∵ ∠A=90?,
∴ ∠2+∠3=90?,
∴ ∠1=∠3;
同理可得∠2=∠4.
17.
【答案】
证明:延长AP交BC与点M,根据三角形的外角性质,得
∠APB=∠θ+∠PMB,∠PMB=∠α+∠β,
∴ ∠APB=α+β+θ.
【解答】
证明:延长AP交BC与点M,根据三角形的外角性质,得
∠APB=∠θ+∠PMB,∠PMB=∠α+∠β,
∴ ∠APB=α+β+θ.
一、 选择题
1. 如图,在△ABC中,点D在BC的延长线上,若∠A=60?,∠B=40?,则∠ACD的度数是(? ? ? ? )
A.140? B.120? C.110? D.100?
2. 如图,若∠B=35??,∠ACD=120??,则∠A=(? ? ? ? )
A.35?? B.75?? C.85?? D.95??
3. 如图,图中∠1的大小等于(? ? ? ? )?
A.40? B.50? C.60? D.70?
4. 如图,∠1=45?,∠3=105?,则∠2的度数为( )
A.60? B.55? C.35? D.30?
5. 如图,∠A,∠DOE,∠BEC的大小关系是( )
A.∠A>∠DOE>∠BEC B.∠DOE>∠BEC>∠A
C.∠DOE>∠A>∠BEC D.∠BEC>∠DOE>∠A
6. 如图,在△ABC中,∠ACB=90?,沿CD折叠△CBD,使点B恰好落在边AC上点E处,若∠A=25?,则∠ADE的大小为( )
A.40? B.50? C.65? D.75?
7. 如图,在△ABC中,∠ACB=90?,沿CD折叠△CBD,使点B恰好落在AC边上的点E处,若∠A=20?,则∠BDC的度数为( )
A.70? B.65? C.60? D.40?
8. 已知△ABC的外角∠CBE,∠BCF的角平分线BP,CP交于P点,则∠BPC是( )
A.钝角 B.锐角 C.直角 D.无法确定
9. 如图所示,一副三角板放在两条平行线MN,PQ之间,含30?角的三角板的较长直角边在直线PQ上,含45?角的三角板的一条直角边在另一个三角板的斜边上,则∠NAC的度数是(? ? ? ? )
A.100? B.108? C.110? D.120?
10. 如图,将纸片△ABC沿着DE折叠,若∠1+∠2=60?,则∠A的大小为( )
A.20? B.25? C.30? D.35?
二、 填空题 ?
11. △ABC中,∠B=∠A+10?,∠C=∠B+10?,则∠A=________??.
12. 在直角三角形中,两个锐角的度数比为2:3,那么较小锐角的度数是________.
13. 如图,在四边形ABCD中,∠A与∠DCB互补,E为BC延长线上的点,且∠1+∠2+∠DCE=224?,则∠A的度数是________.
14. 如图,在△ABC中,BO,CO分别平分∠ABC和∠ACB,∠A=100?,则∠BOC=________度.
三、 解答题 ?
15. 如图,在△ABC中,∠ACB=90?,CD是△ABC的一条高线,若∠B=28?.求∠ACD的度数.
?
16. 如图,∠A=∠C=∠BED=90?,求证:∠1=∠3,∠2=∠4.
?
17. 如图所示,直线a和b相交于点C,∠C=β,AP,BP交于点P,且∠PAC=α,∠PBC=θ,求证:∠APB=α+β+θ.
参考答案与试题解析
一、 选择题
1.
【答案】
D
【解答】
解:∵ ∠ACD是△ABC的一个外角,
∴ ∠ACD=∠A+∠B,
∵ ∠A=60?,∠B=40?,
∴ ∠ACD=60?+40?=100?.
故选D.
2.
【答案】
C
【解答】
解:由题意可得:?∠A=∠ACD?∠B=120??35?=85?.
故选C.
3.
【答案】
D
【解答】
解:由三角形的外角性质得,∠1=130??60?=70?.
故选D.
4.
【答案】
A
【解答】
此题暂无解答
5.
【答案】
B
【解答】
解:∵ ∠BEC是△ABE的外角,
∴ ∠BEC>∠A,
∵ ∠DOE是△COE的外角,
∴ ∠DOE>∠BEC,
∴ ∠DOE>∠BEC>∠A,
故选:B.
6.
【答案】
A
【解答】
∵ 在△ABC中,∠ACB=90?,∠A=25?,
∴ ∠B=180??90??25?=65?,
根据折叠可得∠CED=65?,
∴ ∠ADE=65??25?=40?,
7.
【答案】
B
【解答】
此题暂无解答
8.
【答案】
B
【解答】
解:∵ △ABC的外角平分线BP,CP交于P点,
∴ ∠PBC=12∠EBC,∠BCP=12∠BCF,
∵ ∠CBE、∠BCF是△ABC的两个外角,
∴ ∠CBE+∠BCF=360??(180??∠A)=180?+∠A,
∴ ∠PBC+∠BCP=12(∠EBC+∠BCF)=12(180?+∠A)=90?+12∠A,
∵ 在△PBC中,∠BPC=180??(∠PBC+∠BCP)=180??(90?+12∠A)=90??12∠A<90?,
∴ ∠BPC是锐角.
故选:B.
9.
【答案】
D
【解答】
解:延长AC交PQ于点G,则∠GCB=90?,
∴ ∠AGQ=60?.
∵ PQ//MN,
∴ ∠NAC+∠AGQ=180?,
∴ ∠NAC=180??60?=120?.
故选D.
10.
【答案】
C
【解答】
根据折叠及邻补角的性质,得
∠1=180??2∠ADE,∠2=180??2∠AED,
∴ ∠1+∠2=360??2(∠ADE+∠AED),
∵ ∠1+∠2=60?
∴ ∠ADE+∠AED=150?,
∴ 在△ADE中,由内角和定理,得
∠A=180??(∠ADE+∠AED)=30?,
二、 填空题
11.
【答案】
50?
【解答】
此题暂无解答
12.
【答案】
36?
【解答】
解:设两锐角分别为2k、3k,由题意得
2k+3k=90?
解得k=18?
所以较小锐角的度数为18×2=36?
故答案为:36?.
13.
【答案】
[加加)112?
【解答】
此题暂无解答
14.
【答案】
140
【解答】
此题暂无解答
三、 解答题
15.
【答案】
解:∵ ∠ACB=90?,
∴ ∠ACD+∠BCD=90?,
∵ CD是△ABC的一条高线,
∴ ∠B+∠BCD=90?,
∴ ∠ACD=∠B=28?.
【解答】
解:∵ ∠ACB=90?,
∴ ∠ACD+∠BCD=90?,
∵ CD是△ABC的一条高线,
∴ ∠B+∠BCD=90?,
∴ ∠ACD=∠B=28?.
16.
【答案】
证明:∵ ∠BED=90?,
∴ ∠1+∠2=180??90?=90?,
∵ ∠A=90?,
∴ ∠2+∠3=90?,
∴ ∠1=∠3;
同理可得∠2=∠4.
【解答】
证明:∵ ∠BED=90?,
∴ ∠1+∠2=180??90?=90?,
∵ ∠A=90?,
∴ ∠2+∠3=90?,
∴ ∠1=∠3;
同理可得∠2=∠4.
17.
【答案】
证明:延长AP交BC与点M,根据三角形的外角性质,得
∠APB=∠θ+∠PMB,∠PMB=∠α+∠β,
∴ ∠APB=α+β+θ.
【解答】
证明:延长AP交BC与点M,根据三角形的外角性质,得
∠APB=∠θ+∠PMB,∠PMB=∠α+∠β,
∴ ∠APB=α+β+θ.
