贵州省兴义七中2012届高考数学二轮复习资料:函数的应用
文档属性
| 名称 | 贵州省兴义七中2012届高考数学二轮复习资料:函数的应用 |  | |
| 格式 | zip | ||
| 文件大小 | 58.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-17 15:16:15 | ||
图片预览

文档简介
贵州省兴义七中2012届高考数学二轮复习资料:函数的应用
I 卷
一、选择题
1. 函数零点所在的区间是 ( )
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
【答案】C
2.函数y=loga(x+1)+x2-2(0<a<1)的零点的个数为( )
A.0 B.1
C.2 D.无法确定
【答案】C
3.用二分法判断方程()x=x2的根的个数是( )
A.4个 B.3个
C.2个 D.1个
【答案】C
4.若函数f(x)=x3+x2-2x-2的一个正数零点用二分法计算,附近的函数值参考数据如下:
f(1)=-2 f(1.5)=0.625 f(1.25)=-0.984
f(1.375)=-0.260 f(1.4375)=0.162 f(1.40625)=-0.054
那么方程x3+x2-2x-2=0的一个近似根(精确度0.1)为( )
A.1.25 B.1.375
C.1.4375 D.1.5
【答案】C
5.已知函数则函数f(x)的零点个数为 ( )
A.1 B.2 C.3 D.4
【答案】C
6.定义在R上的奇函数f(x)( )
A.未必有零点
B.零点的个数为偶数
C.至少有一个零点
D.以上都不对
【答案】C
II卷
二、填空题
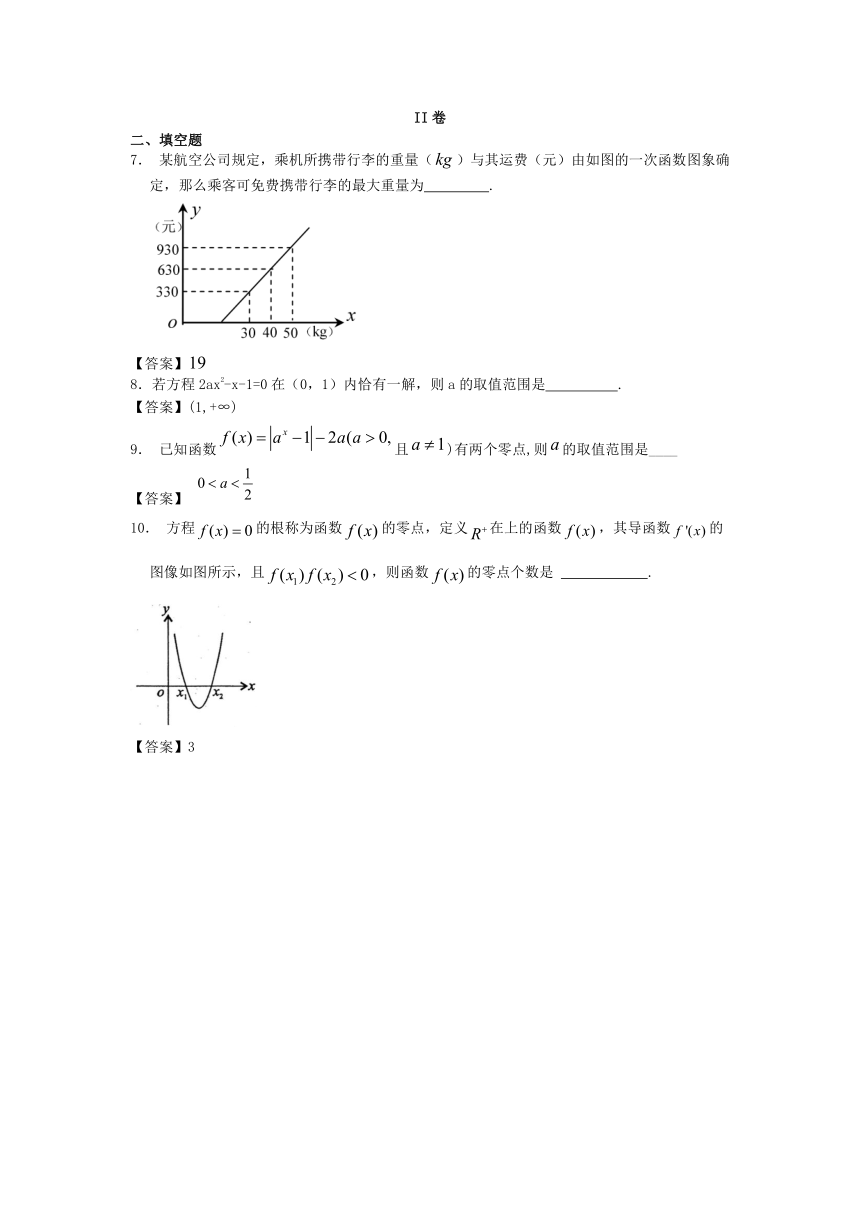
7. 某航空公司规定,乘机所携带行李的重量()与其运费(元)由如图的一次函数图象确定,那么乘客可免费携带行李的最大重量为 .
【答案】
8.若方程2ax2-x-1=0在(0,1)内恰有一解,则a的取值范围是 .
【答案】(1,+∞)
9. 已知函数且)有两个零点,则的取值范围是____
【答案】
10. 方程的根称为函数的零点,定义在上的函数,其导函数的图像如图所示,且,则函数的零点个数是 .
【答案】3
三、解答题
11.已知函数是函数的极值点.
(1)求实数的值;
(2)若方程有两个不相等的实数根,求实数m的取值.
【答案】 (1)
,
由已知,.
(2)由(1)
.
令,当时:
x 1
- 0 +
极小值
所以,要使方程有两不相等的实数根,即函数的图象与直线有两个不同的交点, m=0或.
12.若方程x2-2ax+a=0在(0,1)恰有一个解,求a的取值范围.
【答案】设f(x)=x2-2ax+a.
由题意知:f(0)·f(1)<0,
即a(1-a)<0,根据两数之积小于0,那么必然一正一负.故分为两种情况.
∴a<0或a>1.
13.确定函数f(x)=logx+x-4的零点个数.
【答案】
设y1=logx,y2=4-x,则f(x)的零点个数,即y1与y2的交点个数,作出两函数图象如图.
由图知,y1与y2在区间(0,1)内有一个交点,
当x=4时,y1=-2,y2=0;
当x=8时,y1=-3,y2=-4,
∴在(4,8)内两曲线又有一个交点,
∴两曲线有两个交点,
即函数f(x)=logx+x-4有两个零点.
14.已知函数f(x)=2x3-x2+ax+1-a2在(-∞,+∞)上是增函数.若函数的零点属于区间(0,1),求实数a的取值范围.
【答案】由于f(x)在(-∞,+∞)上是增函数,故f(x)只有一个零点,
依题意有f (0)f(1)<0,
即(1-a2)(2-1+a+1-a2)<0,解得1即a的取值范围是(1,2).
15.将进货价为8元的商品按每件10元售出,每天可销售200件;若每件的售价涨0.5元,其销售量减少10件,问将售价定为多少时,才能使所赚利润最大?并求出这个最大利润.
【答案】设每件售价提高x元,利润为y元,
则y=(2+x)(200-20x)=-20(x-4)2+720.
故当x=4,即定价为14元时,每天可获利最多为720元.
16.燕子每年秋天都要从北方飞向南方过冬,研究燕子的科学家发现,两岁燕子的飞行速度可以表示为函数v=5log2,单位是ms,其中Q表示燕子的耗氧量.
(1)试计算:燕子静止时的耗氧量是多少个单位?
(2)当一只燕子的耗氧量是80个单位时,它的飞行速度是多少?
【答案】(1)由题意知,当燕子静止时,它的速度为0,代入题目所给公式可得
0=5log2,解得Q=10,
即燕子静止时的耗氧量为10个单位.
(2)将耗氧量Q=80代入公式得
v=5log2=5log28=15(ms),
即当一只燕子耗氧量为80个单位时,它的飞行速度为15ms.
17.物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始温度是T0,经过一定时间t后的温度是T,则T-Ta=(T0-Ta)·(),其中Ta表示环境温度,h称为半衰期.
现有一杯用88 ℃热水冲的速溶咖啡,放在24 ℃的房间中,如果咖啡降温到40 ℃需要20 min,那么降温到35 ℃时,需要多长时间?
【答案】由题意知40-24=(88-24)·(),
即=().
解之,得h=10.
故T-24=(88-24)·().
当T=35时,代入上式,得
35-24=(88-24)·(),
即()=.
两边取对数,用计算器求得t≈25.
因此,约需要25 min,可降温到35 ℃.
18.某送外卖的个体户,从食品加工店买进营养早餐的价格是每份2元,卖出价是每份3元,卖不掉的早餐可以以每份0.5元价格卖给养殖户.在一个月(以30天计)里,周末(8天计)只能卖出60份,其余22天每天可卖出80份,但每天从加工店买进的份数必须相同,这个个体户每天从食品加工店买进多少份,才能使每月所获的利润最大?并计算他一个月可赚得多少元?
【答案】设个体户每天从食品加工店买进营养早餐x份,
显然当x∈[60,80]时,每月所获利润才能最大.
于是每月所获利润为
y=22×3x+8×3×60+8×0.5×(x-60)-30×2x
=10x+1 200.
因函数y在[60,80]上为增函数,
故当x= 80时,y有最大值2 000.
所以这个个体户每天从食品加工店买进80份时,才能使每月所获的利润最大,这样他一个月可赚2 000元.
I 卷
一、选择题
1. 函数零点所在的区间是 ( )
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
【答案】C
2.函数y=loga(x+1)+x2-2(0<a<1)的零点的个数为( )
A.0 B.1
C.2 D.无法确定
【答案】C
3.用二分法判断方程()x=x2的根的个数是( )
A.4个 B.3个
C.2个 D.1个
【答案】C
4.若函数f(x)=x3+x2-2x-2的一个正数零点用二分法计算,附近的函数值参考数据如下:
f(1)=-2 f(1.5)=0.625 f(1.25)=-0.984
f(1.375)=-0.260 f(1.4375)=0.162 f(1.40625)=-0.054
那么方程x3+x2-2x-2=0的一个近似根(精确度0.1)为( )
A.1.25 B.1.375
C.1.4375 D.1.5
【答案】C
5.已知函数则函数f(x)的零点个数为 ( )
A.1 B.2 C.3 D.4
【答案】C
6.定义在R上的奇函数f(x)( )
A.未必有零点
B.零点的个数为偶数
C.至少有一个零点
D.以上都不对
【答案】C
II卷
二、填空题
7. 某航空公司规定,乘机所携带行李的重量()与其运费(元)由如图的一次函数图象确定,那么乘客可免费携带行李的最大重量为 .
【答案】
8.若方程2ax2-x-1=0在(0,1)内恰有一解,则a的取值范围是 .
【答案】(1,+∞)
9. 已知函数且)有两个零点,则的取值范围是____
【答案】
10. 方程的根称为函数的零点,定义在上的函数,其导函数的图像如图所示,且,则函数的零点个数是 .
【答案】3
三、解答题
11.已知函数是函数的极值点.
(1)求实数的值;
(2)若方程有两个不相等的实数根,求实数m的取值.
【答案】 (1)
,
由已知,.
(2)由(1)
.
令,当时:
x 1
- 0 +
极小值
所以,要使方程有两不相等的实数根,即函数的图象与直线有两个不同的交点, m=0或.
12.若方程x2-2ax+a=0在(0,1)恰有一个解,求a的取值范围.
【答案】设f(x)=x2-2ax+a.
由题意知:f(0)·f(1)<0,
即a(1-a)<0,根据两数之积小于0,那么必然一正一负.故分为两种情况.
∴a<0或a>1.
13.确定函数f(x)=logx+x-4的零点个数.
【答案】
设y1=logx,y2=4-x,则f(x)的零点个数,即y1与y2的交点个数,作出两函数图象如图.
由图知,y1与y2在区间(0,1)内有一个交点,
当x=4时,y1=-2,y2=0;
当x=8时,y1=-3,y2=-4,
∴在(4,8)内两曲线又有一个交点,
∴两曲线有两个交点,
即函数f(x)=logx+x-4有两个零点.
14.已知函数f(x)=2x3-x2+ax+1-a2在(-∞,+∞)上是增函数.若函数的零点属于区间(0,1),求实数a的取值范围.
【答案】由于f(x)在(-∞,+∞)上是增函数,故f(x)只有一个零点,
依题意有f (0)f(1)<0,
即(1-a2)(2-1+a+1-a2)<0,解得1
15.将进货价为8元的商品按每件10元售出,每天可销售200件;若每件的售价涨0.5元,其销售量减少10件,问将售价定为多少时,才能使所赚利润最大?并求出这个最大利润.
【答案】设每件售价提高x元,利润为y元,
则y=(2+x)(200-20x)=-20(x-4)2+720.
故当x=4,即定价为14元时,每天可获利最多为720元.
16.燕子每年秋天都要从北方飞向南方过冬,研究燕子的科学家发现,两岁燕子的飞行速度可以表示为函数v=5log2,单位是ms,其中Q表示燕子的耗氧量.
(1)试计算:燕子静止时的耗氧量是多少个单位?
(2)当一只燕子的耗氧量是80个单位时,它的飞行速度是多少?
【答案】(1)由题意知,当燕子静止时,它的速度为0,代入题目所给公式可得
0=5log2,解得Q=10,
即燕子静止时的耗氧量为10个单位.
(2)将耗氧量Q=80代入公式得
v=5log2=5log28=15(ms),
即当一只燕子耗氧量为80个单位时,它的飞行速度为15ms.
17.物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始温度是T0,经过一定时间t后的温度是T,则T-Ta=(T0-Ta)·(),其中Ta表示环境温度,h称为半衰期.
现有一杯用88 ℃热水冲的速溶咖啡,放在24 ℃的房间中,如果咖啡降温到40 ℃需要20 min,那么降温到35 ℃时,需要多长时间?
【答案】由题意知40-24=(88-24)·(),
即=().
解之,得h=10.
故T-24=(88-24)·().
当T=35时,代入上式,得
35-24=(88-24)·(),
即()=.
两边取对数,用计算器求得t≈25.
因此,约需要25 min,可降温到35 ℃.
18.某送外卖的个体户,从食品加工店买进营养早餐的价格是每份2元,卖出价是每份3元,卖不掉的早餐可以以每份0.5元价格卖给养殖户.在一个月(以30天计)里,周末(8天计)只能卖出60份,其余22天每天可卖出80份,但每天从加工店买进的份数必须相同,这个个体户每天从食品加工店买进多少份,才能使每月所获的利润最大?并计算他一个月可赚得多少元?
【答案】设个体户每天从食品加工店买进营养早餐x份,
显然当x∈[60,80]时,每月所获利润才能最大.
于是每月所获利润为
y=22×3x+8×3×60+8×0.5×(x-60)-30×2x
=10x+1 200.
因函数y在[60,80]上为增函数,
故当x= 80时,y有最大值2 000.
所以这个个体户每天从食品加工店买进80份时,才能使每月所获的利润最大,这样他一个月可赚2 000元.
