贵州省兴义七中2012届高考数学二轮复习资料:空间几何体
文档属性
| 名称 | 贵州省兴义七中2012届高考数学二轮复习资料:空间几何体 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-17 00:00:00 | ||
图片预览


文档简介
贵州省兴义七中2012届高考数学二轮复习资料:空间几何体
I 卷
一、选择题
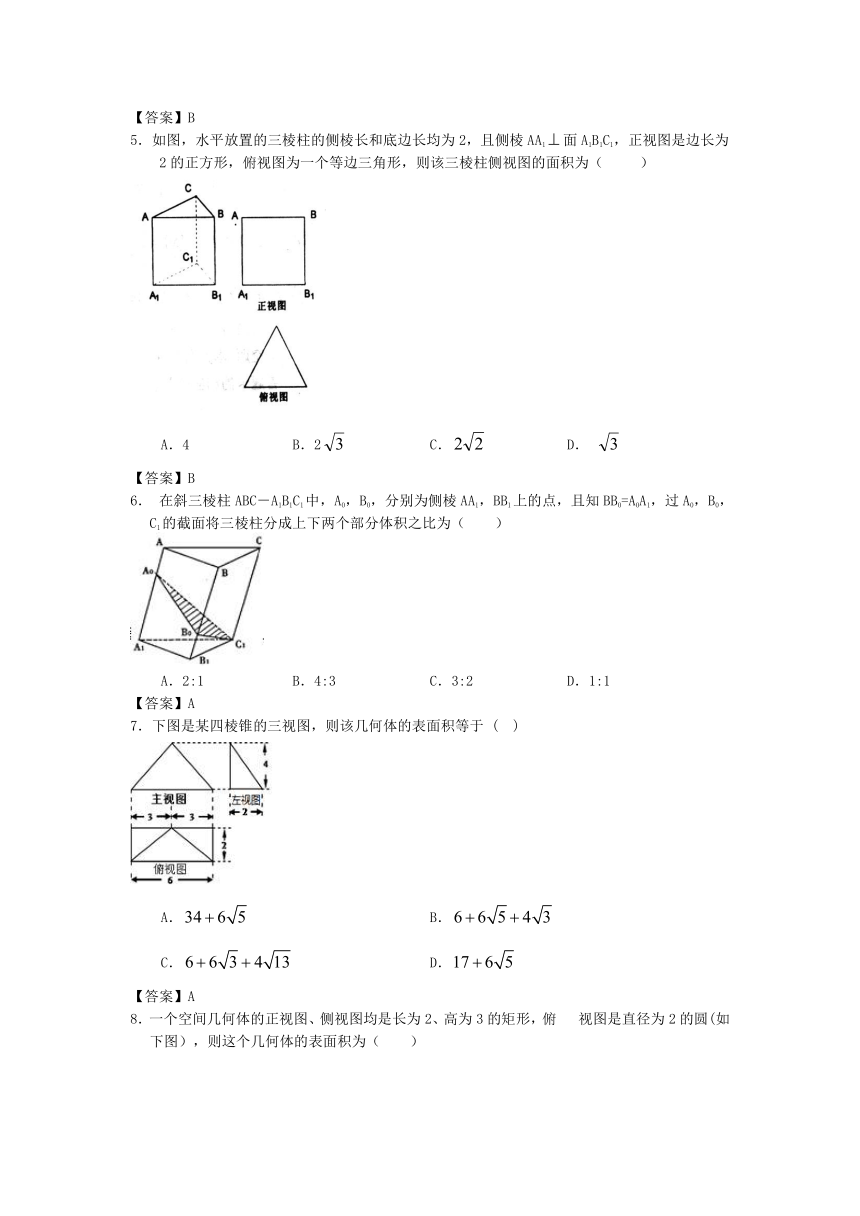
1.在正三棱锥S-ABC中,侧面SAB、侧面SAC、侧面SBC两两垂直,且侧棱SA=,则正三棱 S-ABC外接球的表面积为( )
A.12 B.32 C.36 D.48
【答案】C
2.某几何体的三视图如图所示,则该几何体的体积为 ( )
A. B. C. D.
【答案】A
3.下列四个几何体中,各几何体的三视图有且仅有两个视图相同的是( )
A.①② B.②③ C.②④ D.①③
【答案】C
解析:①的三个视图都相同;②的主视图与左视图相同,与俯视图不同;③的三个视图互不相同;④的主视图与左视图相同,而与俯视图不同。
4. 如图所示,已知正四棱锥S—ABCD侧棱长为,底面边长为,E是SA的中点,则异面直线BE与SC所成角的大小为 ( )
A.90° B.60° C.45° D.30°
【答案】B
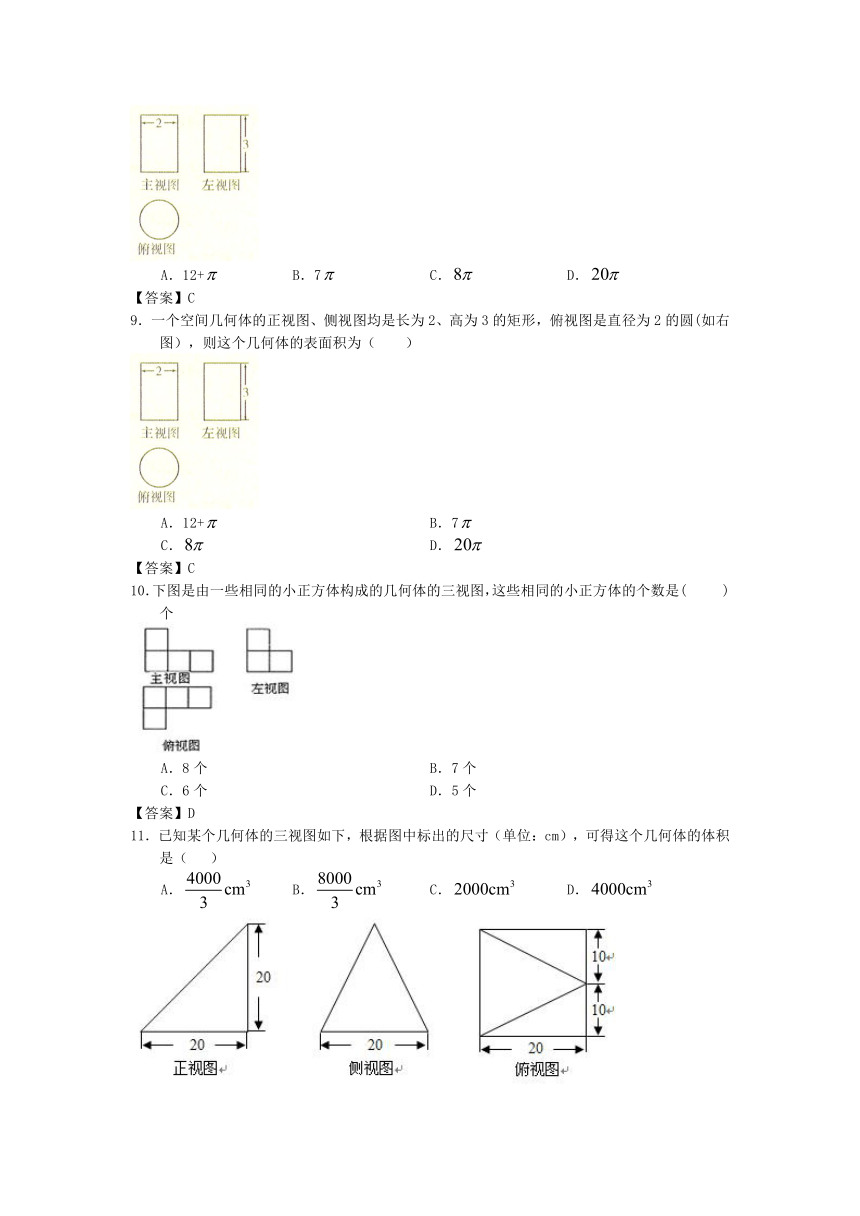
5.如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形,则该三棱柱侧视图的面积为( )
A.4 B.2 C. D.
【答案】B
6. 在斜三棱柱ABC-A1B1C1中,A0,B0,分别为侧棱AA1,BB1上的点,且知BB0=A0A1,过A0,B0,C1的截面将三棱柱分成上下两个部分体积之比为( )
A.2:1 B.4:3 C.3:2 D.1:1
【答案】A
7.下图是某四棱锥的三视图,则该几何体的表面积等于 ( )
A. B.
C. D.
【答案】A
8.一个空间几何体的正视图、侧视图均是长为2、高为3的矩形,俯 视图是直径为2的圆(如下图),则这个几何体的表面积为( )
A.12+ B.7 C. D.
【答案】C
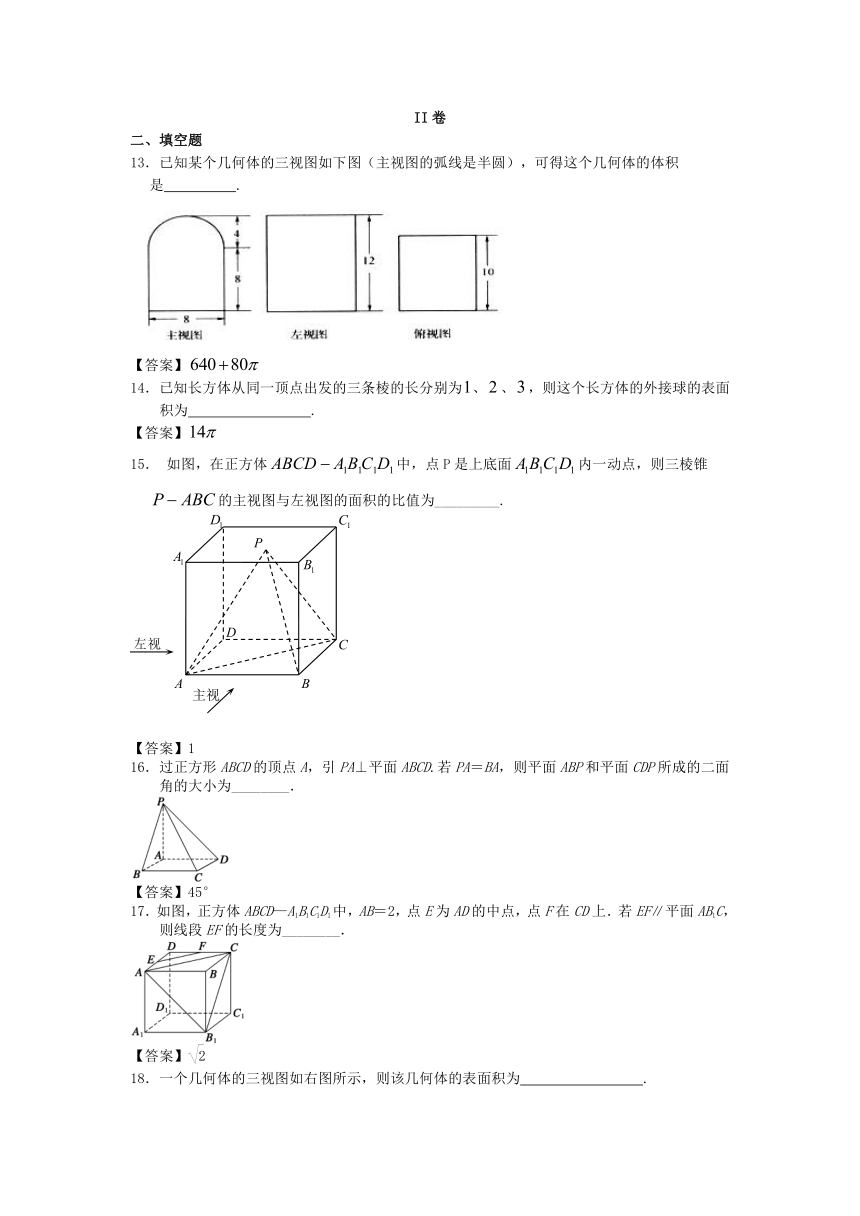
9.一个空间几何体的正视图、侧视图均是长为2、高为3的矩形,俯视图是直径为2的圆(如右图),则这个几何体的表面积为( )
A.12+ B.7
C. D.
【答案】C
10.下图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体的个数是( )个
A.8个 B.7个
C.6个 D.5个
【答案】D
11.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
A. B. C. D.
【答案】B
12. 一个二面角的两个面分别垂直于另一个二面角的两个面,那么这两个二面角( )
A.相等 B.互补 C.相等或互补 D.不能确定
【答案】D
II卷
二、填空题
13.已知某个几何体的三视图如下图(主视图的弧线是半圆),可得这个几何体的体积是 .
【答案】
14.已知长方体从同一顶点出发的三条棱的长分别为、、,则这个长方体的外接球的表面积为 .
【答案】
15. 如图,在正方体中,点P是上底面内一动点,则三棱锥的主视图与左视图的面积的比值为_________.
【答案】1
16.过正方形ABCD的顶点A,引PA⊥平面ABCD.若PA=BA,则平面ABP和平面CDP所成的二面角的大小为________.
【答案】45°
17.如图,正方体ABCD—A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度为________.
【答案】
18.一个几何体的三视图如右图所示,则该几何体的表面积为 .
【答案】24+12
三、解答题
19.直三棱柱ABC -A1B1C1中,AB=5,
AC=4,BC=3,AA1=4,点D在AB上.
(Ⅰ)求证:AC⊥B1C;
(Ⅱ)若D是AB中点,求证:AC1∥平面B1CD;
(Ⅲ)当时,求二面角的余弦值.
【答案】(Ⅰ)在△ABC中,因为 AB=5,AC=4,BC=3,
所以 AC2+ BC2= AB2, 所以 AC⊥BC.
因为 直三棱柱ABC-A1B1C1,所以 C C1⊥AC.
因为 BC∩AC =C,所以 AC⊥平面B B1C1C.
所以 AC⊥B1C.
(Ⅱ)证明:连结BC1,交B1C于E,连接DE.
因为 直三棱柱ABC-A1B1C1,D是AB中点,所以 侧面B B1C1C为矩形,DE为△ABC1的中位线,
所以 DE AC1.因为 DE平面B1CD, AC1平面B1CD,所以 AC1∥平面B1CD.
(Ⅲ)由(Ⅰ)知AC⊥BC,如图,以C为原点建立空间直角坐标系C-xyz.
则B (3, 0, 0),A (0, 4, 0),A1 (0, 4, 4),B1 (3, 0, 4).
设D (a, b, 0)(,),
因为 点D在线段AB上,且,即.
所以,,,, ,.
平面BCD的法向量为. 设平面B1 CD的法向量为,
由 ,, 得 ,
所以 ,,.所以 .
所以二面角的余弦值为.
20.已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点。
(1)求四棱锥P-ABCD的体积;
(2)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
(3)求四棱锥P-ABCD的侧面积.
【答案】由该四棱锥的三视图可知,该四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC=2. ∴
(2) 不论点E在何位置,都有BD⊥AE。证明如下:连结AC,∵ABCD是正方形
∴BD⊥AC ∵PC⊥底面ABCD 且平面 ∴BD⊥PC-
又∵ ∴BD⊥平面PAC ∵不论点E在何位置,都有AE平面PAC
∴不论点E在何位置,都有BD⊥AE
(3) 由(1)知PC⊥CD,PC⊥BC,CD=CB, ∴Rt△PCD≌Rt△PCB
∵AB⊥BC,AB⊥PC, ∴AB⊥平面PCB ∵PB平面PBC,∴AB⊥PB
同理AD⊥PD,∴四棱锥P-ABCD的侧面积==2+
21.如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,,AE∥CD,DC=AC=2AE=2.
(Ⅰ)求证:平面BCD平面ABC
(Ⅱ)求证:AF∥平面BDE;
(Ⅲ)求四面体B-CDE的体积.
【答案】(Ⅰ)∵面ABC面ACDE,面ABC面ACDE=AC,CDAC,
∴DC面ABC,
又∵DC面BCD,∴平面BCD平面ABC.
(Ⅱ)取BD的中点P,连结EP、FP,则PF DC,
又∵EADC,∴EAPF,
∴四边形AFPE是平行四边形,∴AF∥EP,
又∵EP面BDE,∴AF∥面BDE.
(Ⅲ)∵BAAC,面ABC面ACDE=AC,∴BA面ACDE.
∴BA就是四面体B-CDE的高,且BA=2.
∵DC=AC=2AE=2,AE∥CD,
∴
∴ ∴
22.如图所示的几何体是由以等边三角形为底面的棱柱被平面所截而得,已知平面,为的中点
(1)求证:∥平面
(2)求证:平面平面
(3)求平面与平面相交所成锐角二面角的余弦值
【答案】⑴取DE D中点G,建系如图,则A(0,,0)、B(0,-1,0)、C(1,0,0)、
D(-1,0,1),E(1,0,3)、F(0,,2)、G(0,0,2),
设平面DEF的一法向量=(x,y,z),
⑵显然,平面BCED的一法向量为=(0,1,0),=0,∴平面DEF︿平面BCED
⑶由⑴知平面DEF的一法向量=(1,0,-1),平面ABC的一法向量=(0,0,1),
cos<,>= eq \f(,||||) =-
∴求平面与平面相交所成锐角二面角的余弦值为 .
23.如图,在斜三棱柱 中,,,侧面与底面ABC所成的二面角为120,E、F分别是棱、的中点。
(Ⅰ)求与底面ABC所成的角;
(Ⅱ)证明EA1∥平面.
【答案】(I)过作平面平面,垂足为.连接,并延长交于,连接,于是为与底面所成的角.
因为,所以为的平分线
又因为,所以,且为的中点
因此,由三垂线定理
因为,且,所以,
于是为二面角的平面角,即
由于四边形为平行四边形,得
所以,与底面所成的角度为
(II) 证明:设与的交点为,则点P为EG的中点,连结PF.
在平行四边形中,因为F是的中点,所以
而EP平面,平面,所以平面
24.如图,平面ABCD⊥平面PAD,△APD是直角三角形,∠APD=90°,四边形ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=2BC,
O是AD的中点.
(1)求证:CD∥平面PBO;
(2)求证:平面PAB⊥平面PCD.
【答案】(1)∵AD=2BC,且O是AD中点,
∴OD=BC,又AD∥BC,
∴OD∥BC,
∴四边形BCDO为平行四边形,
∴CD∥BO,CD 平面PBO,
且BO 平面PBO,故CD∥平面PBO.
(2)∵∠BAD=90°,∴BA⊥AD,
又平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,
AB 平面ABCD,
∴AB⊥平面PAD,PD 平面PAD,
∴AB⊥PD.
∵AP⊥PD,AB∩AP=A,
∴PD⊥平面PAB,
又∵PD 平面PCD,
故平面PAB⊥平面PCD.
25.已知如图几何体,正方形和矩形所在平面互相垂直,,为的中点,。
(Ⅰ)求证: ;
(Ⅱ)求二面角 的大小。
【答案】(I)连结交于,连结
因为为中点,为中点,
所以,
又因为,
所以;
(II)因为正方形和矩形所在平面互相垂直,
所以
以为原点,以为轴建立空间直角坐标系,如图取=1
,,,,
设平面的法向量为 = (x ,y , z ),
设平面的法向量为 = (x ,y , z ),
所以二面角 的大小为。
26.一个多面体的直观图如图所示(其中分别为的中点)
(1)求证:平面
(2)求多面体的体积
【答案】由三视图可知,该多面体是底面为直角三角形的直三棱柱,且,,
取的中点,连,由分别为中点可得,
平面平面,平面。
取中点,在直三棱柱中,平面平面,面面,面,多面体是以为高,以矩形为底面的棱锥,在中,棱锥的体积。
I 卷
一、选择题
1.在正三棱锥S-ABC中,侧面SAB、侧面SAC、侧面SBC两两垂直,且侧棱SA=,则正三棱 S-ABC外接球的表面积为( )
A.12 B.32 C.36 D.48
【答案】C
2.某几何体的三视图如图所示,则该几何体的体积为 ( )
A. B. C. D.
【答案】A
3.下列四个几何体中,各几何体的三视图有且仅有两个视图相同的是( )
A.①② B.②③ C.②④ D.①③
【答案】C
解析:①的三个视图都相同;②的主视图与左视图相同,与俯视图不同;③的三个视图互不相同;④的主视图与左视图相同,而与俯视图不同。
4. 如图所示,已知正四棱锥S—ABCD侧棱长为,底面边长为,E是SA的中点,则异面直线BE与SC所成角的大小为 ( )
A.90° B.60° C.45° D.30°
【答案】B
5.如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形,则该三棱柱侧视图的面积为( )
A.4 B.2 C. D.
【答案】B
6. 在斜三棱柱ABC-A1B1C1中,A0,B0,分别为侧棱AA1,BB1上的点,且知BB0=A0A1,过A0,B0,C1的截面将三棱柱分成上下两个部分体积之比为( )
A.2:1 B.4:3 C.3:2 D.1:1
【答案】A
7.下图是某四棱锥的三视图,则该几何体的表面积等于 ( )
A. B.
C. D.
【答案】A
8.一个空间几何体的正视图、侧视图均是长为2、高为3的矩形,俯 视图是直径为2的圆(如下图),则这个几何体的表面积为( )
A.12+ B.7 C. D.
【答案】C
9.一个空间几何体的正视图、侧视图均是长为2、高为3的矩形,俯视图是直径为2的圆(如右图),则这个几何体的表面积为( )
A.12+ B.7
C. D.
【答案】C
10.下图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体的个数是( )个
A.8个 B.7个
C.6个 D.5个
【答案】D
11.已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
A. B. C. D.
【答案】B
12. 一个二面角的两个面分别垂直于另一个二面角的两个面,那么这两个二面角( )
A.相等 B.互补 C.相等或互补 D.不能确定
【答案】D
II卷
二、填空题
13.已知某个几何体的三视图如下图(主视图的弧线是半圆),可得这个几何体的体积是 .
【答案】
14.已知长方体从同一顶点出发的三条棱的长分别为、、,则这个长方体的外接球的表面积为 .
【答案】
15. 如图,在正方体中,点P是上底面内一动点,则三棱锥的主视图与左视图的面积的比值为_________.
【答案】1
16.过正方形ABCD的顶点A,引PA⊥平面ABCD.若PA=BA,则平面ABP和平面CDP所成的二面角的大小为________.
【答案】45°
17.如图,正方体ABCD—A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度为________.
【答案】
18.一个几何体的三视图如右图所示,则该几何体的表面积为 .
【答案】24+12
三、解答题
19.直三棱柱ABC -A1B1C1中,AB=5,
AC=4,BC=3,AA1=4,点D在AB上.
(Ⅰ)求证:AC⊥B1C;
(Ⅱ)若D是AB中点,求证:AC1∥平面B1CD;
(Ⅲ)当时,求二面角的余弦值.
【答案】(Ⅰ)在△ABC中,因为 AB=5,AC=4,BC=3,
所以 AC2+ BC2= AB2, 所以 AC⊥BC.
因为 直三棱柱ABC-A1B1C1,所以 C C1⊥AC.
因为 BC∩AC =C,所以 AC⊥平面B B1C1C.
所以 AC⊥B1C.
(Ⅱ)证明:连结BC1,交B1C于E,连接DE.
因为 直三棱柱ABC-A1B1C1,D是AB中点,所以 侧面B B1C1C为矩形,DE为△ABC1的中位线,
所以 DE AC1.因为 DE平面B1CD, AC1平面B1CD,所以 AC1∥平面B1CD.
(Ⅲ)由(Ⅰ)知AC⊥BC,如图,以C为原点建立空间直角坐标系C-xyz.
则B (3, 0, 0),A (0, 4, 0),A1 (0, 4, 4),B1 (3, 0, 4).
设D (a, b, 0)(,),
因为 点D在线段AB上,且,即.
所以,,,, ,.
平面BCD的法向量为. 设平面B1 CD的法向量为,
由 ,, 得 ,
所以 ,,.所以 .
所以二面角的余弦值为.
20.已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点。
(1)求四棱锥P-ABCD的体积;
(2)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
(3)求四棱锥P-ABCD的侧面积.
【答案】由该四棱锥的三视图可知,该四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC=2. ∴
(2) 不论点E在何位置,都有BD⊥AE。证明如下:连结AC,∵ABCD是正方形
∴BD⊥AC ∵PC⊥底面ABCD 且平面 ∴BD⊥PC-
又∵ ∴BD⊥平面PAC ∵不论点E在何位置,都有AE平面PAC
∴不论点E在何位置,都有BD⊥AE
(3) 由(1)知PC⊥CD,PC⊥BC,CD=CB, ∴Rt△PCD≌Rt△PCB
∵AB⊥BC,AB⊥PC, ∴AB⊥平面PCB ∵PB平面PBC,∴AB⊥PB
同理AD⊥PD,∴四棱锥P-ABCD的侧面积==2+
21.如图所示,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,,AE∥CD,DC=AC=2AE=2.
(Ⅰ)求证:平面BCD平面ABC
(Ⅱ)求证:AF∥平面BDE;
(Ⅲ)求四面体B-CDE的体积.
【答案】(Ⅰ)∵面ABC面ACDE,面ABC面ACDE=AC,CDAC,
∴DC面ABC,
又∵DC面BCD,∴平面BCD平面ABC.
(Ⅱ)取BD的中点P,连结EP、FP,则PF DC,
又∵EADC,∴EAPF,
∴四边形AFPE是平行四边形,∴AF∥EP,
又∵EP面BDE,∴AF∥面BDE.
(Ⅲ)∵BAAC,面ABC面ACDE=AC,∴BA面ACDE.
∴BA就是四面体B-CDE的高,且BA=2.
∵DC=AC=2AE=2,AE∥CD,
∴
∴ ∴
22.如图所示的几何体是由以等边三角形为底面的棱柱被平面所截而得,已知平面,为的中点
(1)求证:∥平面
(2)求证:平面平面
(3)求平面与平面相交所成锐角二面角的余弦值
【答案】⑴取DE D中点G,建系如图,则A(0,,0)、B(0,-1,0)、C(1,0,0)、
D(-1,0,1),E(1,0,3)、F(0,,2)、G(0,0,2),
设平面DEF的一法向量=(x,y,z),
⑵显然,平面BCED的一法向量为=(0,1,0),=0,∴平面DEF︿平面BCED
⑶由⑴知平面DEF的一法向量=(1,0,-1),平面ABC的一法向量=(0,0,1),
cos<,>= eq \f(,||||) =-
∴求平面与平面相交所成锐角二面角的余弦值为 .
23.如图,在斜三棱柱 中,,,侧面与底面ABC所成的二面角为120,E、F分别是棱、的中点。
(Ⅰ)求与底面ABC所成的角;
(Ⅱ)证明EA1∥平面.
【答案】(I)过作平面平面,垂足为.连接,并延长交于,连接,于是为与底面所成的角.
因为,所以为的平分线
又因为,所以,且为的中点
因此,由三垂线定理
因为,且,所以,
于是为二面角的平面角,即
由于四边形为平行四边形,得
所以,与底面所成的角度为
(II) 证明:设与的交点为,则点P为EG的中点,连结PF.
在平行四边形中,因为F是的中点,所以
而EP平面,平面,所以平面
24.如图,平面ABCD⊥平面PAD,△APD是直角三角形,∠APD=90°,四边形ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=2BC,
O是AD的中点.
(1)求证:CD∥平面PBO;
(2)求证:平面PAB⊥平面PCD.
【答案】(1)∵AD=2BC,且O是AD中点,
∴OD=BC,又AD∥BC,
∴OD∥BC,
∴四边形BCDO为平行四边形,
∴CD∥BO,CD 平面PBO,
且BO 平面PBO,故CD∥平面PBO.
(2)∵∠BAD=90°,∴BA⊥AD,
又平面PAD⊥平面ABCD,
且平面PAD∩平面ABCD=AD,
AB 平面ABCD,
∴AB⊥平面PAD,PD 平面PAD,
∴AB⊥PD.
∵AP⊥PD,AB∩AP=A,
∴PD⊥平面PAB,
又∵PD 平面PCD,
故平面PAB⊥平面PCD.
25.已知如图几何体,正方形和矩形所在平面互相垂直,,为的中点,。
(Ⅰ)求证: ;
(Ⅱ)求二面角 的大小。
【答案】(I)连结交于,连结
因为为中点,为中点,
所以,
又因为,
所以;
(II)因为正方形和矩形所在平面互相垂直,
所以
以为原点,以为轴建立空间直角坐标系,如图取=1
,,,,
设平面的法向量为 = (x ,y , z ),
设平面的法向量为 = (x ,y , z ),
所以二面角 的大小为。
26.一个多面体的直观图如图所示(其中分别为的中点)
(1)求证:平面
(2)求多面体的体积
【答案】由三视图可知,该多面体是底面为直角三角形的直三棱柱,且,,
取的中点,连,由分别为中点可得,
平面平面,平面。
取中点,在直三棱柱中,平面平面,面面,面,多面体是以为高,以矩形为底面的棱锥,在中,棱锥的体积。
