贵州省兴义七中2012届高考数学二轮复习资料:推理与证明
文档属性
| 名称 | 贵州省兴义七中2012届高考数学二轮复习资料:推理与证明 |  | |
| 格式 | zip | ||
| 文件大小 | 130.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-17 15:16:15 | ||
图片预览



文档简介
贵州省兴义七中2012届高考数学二轮复习资料:推理与证明
I 卷
一、选择题
1. 已知数列的前项和为,且,,可归纳猜想出的表达式为 ( )
A. B. C. D.
【答案】A
2. 设,且=,则下列大小关系式成立的是( ).
A. B.
C. D.
【答案】A
3. 下面使用类比推理,得出正确结论的是 ( )
A.“若,则”类推出“若,则”
B.“若”类推出“”
C.“若” 类推出“ (c≠0)”
D.“” 类推出“”
【答案】C
4. 古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如: .
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数成为正方形数.下列数中及时三角形数又是正方形数的是( )
A.289 B.1024 C.1225 D.1378
【答案】C
5. 用火柴棒摆“金鱼”,如图所示:
按照上面的规律,第个“金鱼”图需要火柴棒的根数为( )
A. B. C. D.
【答案】C
6. 用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:①,这与三角形内角和为相矛盾,不成立;②所以一个三 角形中不能有两个直角;③假设三角形的三个内角、、中有两个直角,不妨设,正确 顺序的序号为( )
A.①②③ B.①③② C.②③① D.③①②
【答案】D
7. 图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第七个叠放的图形中,小正方体木块总数就是( )
A.25 B.66 C.91 D.120
【答案】C
8. 对于函数,若存在区间,使得,则称区间为函数的一个“稳定区间”.现有四个函数:
①; ②, ③ ④.其中存在“稳定区间”的函数有( )
A.①② B.②③ C.③④ D.②④
【答案】B
9. “所有9的倍数都是3的倍数,某奇数是9的倍数,故该奇数是3的倍数.”上述推理( )
A.小前提错 B.结论错 C.正确 D.大前提错
【答案】C
10. 某同学做了一个如图所示的等腰直角三角形形状的数表且把奇数和偶数分别依次排在了数表的奇数行和偶数行,若用a(i,j)表示第 i行从左数第j个数,如a(4,3) = 10,
则a(21,6) = ( )
A.219 B.211 C.209 D.213
【答案】B
II卷
二、填空题
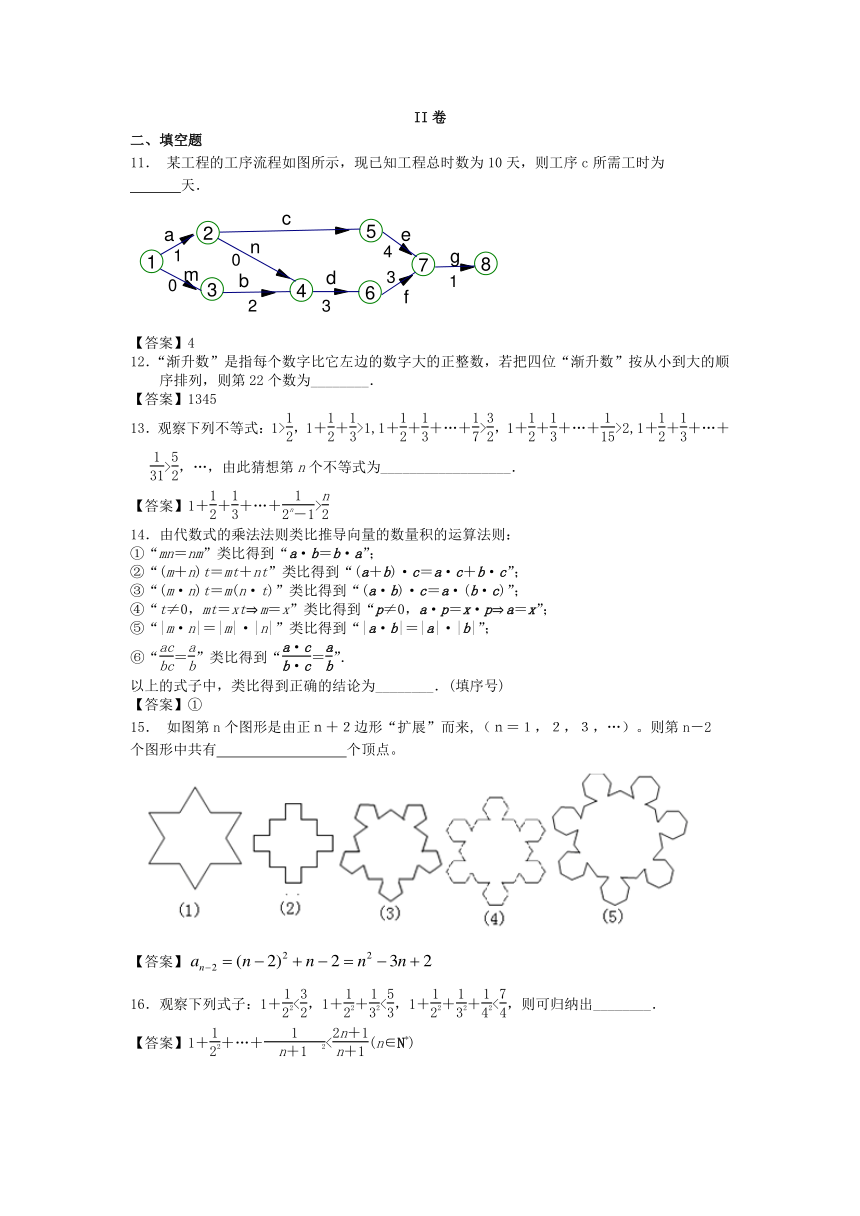
11. 某工程的工序流程如图所示,现已知工程总时数为10天,则工序c所需工时为
天.
【答案】4
12.“渐升数”是指每个数字比它左边的数字大的正整数,若把四位“渐升数”按从小到大的顺序排列,则第22个数为________.
【答案】1345
13.观察下列不等式:1>,1++>1,1+++…+>,1+++…+>2,1+++…+>,…,由此猜想第n个不等式为__________________.
【答案】1+++…+>
14.由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a·b=b·a”;
②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”;
③“(m·n)t=m(n·t)”类比得到“(a·b)·c=a·(b·c)”;
④“t≠0,mt=xt m=x”类比得到“p≠0,a·p=x·p a=x”;
⑤“|m·n|=|m|·|n|”类比得到“|a·b|=|a|·|b|”;
⑥“=”类比得到“=”.
以上的式子中,类比得到正确的结论为________.(填序号)
【答案】①
15. 如图第n个图形是由正n+2边形“扩展”而来,(n=1,2,3,…)。则第n-2
个图形中共有 个顶点。
【答案】
16.观察下列式子:1+<,1++<,1+++<,则可归纳出________.
【答案】1++…+<(n∈N*)
三、解答题
17.设
(Ⅰ)比较与的大小;
(Ⅱ)利用(Ⅰ)的结论,证明:.
【答案】(Ⅰ),∴ .
(Ⅱ)由(1)得
类似的,,
又;
∴
18.我们知道,在△ABC中,若c2=a2+b2,则△ABC是直角三角形,现在请你研究:若cn=an+bn(n>2),问△ABC为何种三角形?为什么?
【答案】令n=3,a=1,b=1,则c=≈1.26,
易观察知△ABC为锐角三角形.
上述特殊值试验的结论具有一般性,下面证明:
因为cn=an+bn(n>2),
所以c>a,c>b,即c是△ABC的最大边.
所以要证△ABC是锐角三角形,
只需证角C为锐角,即证cos C>0.
因为cos C=,
故只需证a2+b2>c2. ①
再注意条件an+bn=cn,于是将①等价变形为
(a2+b2)cn-2>cn(n>2). ②
因为c>a,c>b,n>2,
所以cn-2>an-2,cn-2>bn-2,
即cn-2-an-2>0,cn-2-bn-2>0.
从而(a2+b2)cn-2-cn
=(a2+b2)cn-2-an-bn
=a2(cn-2-an-2)+b2(cn-2-bn-2)>0,
这说明②式成立.
故cos C>0,C是锐角,△ABC为锐角三角形.
19.判断命题“若a>b>c,且a+b+c=0,则<”的真假,并用分析法证明你的结论.
【答案】此命题为真命题,证明过程如下:
∵a+b+c=0,a>b>c,
∴a>0,c<0.
要证<成立,
只需证即证b2-ac<3a2,
只需证(a+c)2-ac<3a2,
即证(a-c)(2a+c)>0,
∵a-c>0,2a+c=(a+c)+a=a-b>0,
∴(a-c)(2a+c)>0成立,故原不等式成立.
20. △ABC的三个内角A、B、C成等差数列, 分别为三个内角A、B、C所对的边,求证: 。
【答案】要证,即需证。
即证。又需证,需证
∵△ABC三个内角A、B、C成等差数列。∴B=60°。
由余弦定理,有,即。
∴成立,命题得证。
21.已知a,b,c为正实数,且a+b+c=1,求证:(-1)(-1)(-1)≥8.
【答案】∵a+b+c=1,且a,b,c为正实数,
∴
=
=
≥2·2·2=8.
22.已知,求证:.
【答案】
要证成立
只需证成立
只需证
只需证
只需证
只需证
只需证
而显然成立,则原不等式得证.
23.已知,且,
(1)求的最小值;
(2)求证:.
【答案】(1)
当且仅当,即时,取到最小值.
(2)
(*)
当且仅当,即,
即,即,
即时,(*)式取到等号.
24.已知:f(x)=x2+px+q.求证:
(1)f(1)+f(3)-2f(2)=2;
(2)|f(1)|,|f(2)|,|f(3)|中至少有一个不小于.
【答案】(1)f(1)+f(3)-2f(2)
=1+p+q+9+3p+q-2(4+2p+q)=2.
(2)反证法:假设|f(1)|,|f(2)|,|f(3)|都小于,
那么2=|f(1)+f(3)-2f(2)|≤|f(1)|+|f(3)|+2|f(2)|<++2·=2矛盾,
所以假设不成立,即|f(1)|,|f(2)|,|f(3)|中至少有一个不小于.
I 卷
一、选择题
1. 已知数列的前项和为,且,,可归纳猜想出的表达式为 ( )
A. B. C. D.
【答案】A
2. 设,且=,则下列大小关系式成立的是( ).
A. B.
C. D.
【答案】A
3. 下面使用类比推理,得出正确结论的是 ( )
A.“若,则”类推出“若,则”
B.“若”类推出“”
C.“若” 类推出“ (c≠0)”
D.“” 类推出“”
【答案】C
4. 古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如: .
他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数成为正方形数.下列数中及时三角形数又是正方形数的是( )
A.289 B.1024 C.1225 D.1378
【答案】C
5. 用火柴棒摆“金鱼”,如图所示:
按照上面的规律,第个“金鱼”图需要火柴棒的根数为( )
A. B. C. D.
【答案】C
6. 用反证法证明命题:“一个三角形中不能有两个直角”的过程归纳为以下三个步骤:①,这与三角形内角和为相矛盾,不成立;②所以一个三 角形中不能有两个直角;③假设三角形的三个内角、、中有两个直角,不妨设,正确 顺序的序号为( )
A.①②③ B.①③② C.②③① D.③①②
【答案】D
7. 图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第七个叠放的图形中,小正方体木块总数就是( )
A.25 B.66 C.91 D.120
【答案】C
8. 对于函数,若存在区间,使得,则称区间为函数的一个“稳定区间”.现有四个函数:
①; ②, ③ ④.其中存在“稳定区间”的函数有( )
A.①② B.②③ C.③④ D.②④
【答案】B
9. “所有9的倍数都是3的倍数,某奇数是9的倍数,故该奇数是3的倍数.”上述推理( )
A.小前提错 B.结论错 C.正确 D.大前提错
【答案】C
10. 某同学做了一个如图所示的等腰直角三角形形状的数表且把奇数和偶数分别依次排在了数表的奇数行和偶数行,若用a(i,j)表示第 i行从左数第j个数,如a(4,3) = 10,
则a(21,6) = ( )
A.219 B.211 C.209 D.213
【答案】B
II卷
二、填空题
11. 某工程的工序流程如图所示,现已知工程总时数为10天,则工序c所需工时为
天.
【答案】4
12.“渐升数”是指每个数字比它左边的数字大的正整数,若把四位“渐升数”按从小到大的顺序排列,则第22个数为________.
【答案】1345
13.观察下列不等式:1>,1++>1,1+++…+>,1+++…+>2,1+++…+>,…,由此猜想第n个不等式为__________________.
【答案】1+++…+>
14.由代数式的乘法法则类比推导向量的数量积的运算法则:
①“mn=nm”类比得到“a·b=b·a”;
②“(m+n)t=mt+nt”类比得到“(a+b)·c=a·c+b·c”;
③“(m·n)t=m(n·t)”类比得到“(a·b)·c=a·(b·c)”;
④“t≠0,mt=xt m=x”类比得到“p≠0,a·p=x·p a=x”;
⑤“|m·n|=|m|·|n|”类比得到“|a·b|=|a|·|b|”;
⑥“=”类比得到“=”.
以上的式子中,类比得到正确的结论为________.(填序号)
【答案】①
15. 如图第n个图形是由正n+2边形“扩展”而来,(n=1,2,3,…)。则第n-2
个图形中共有 个顶点。
【答案】
16.观察下列式子:1+<,1++<,1+++<,则可归纳出________.
【答案】1++…+<(n∈N*)
三、解答题
17.设
(Ⅰ)比较与的大小;
(Ⅱ)利用(Ⅰ)的结论,证明:.
【答案】(Ⅰ),∴ .
(Ⅱ)由(1)得
类似的,,
又;
∴
18.我们知道,在△ABC中,若c2=a2+b2,则△ABC是直角三角形,现在请你研究:若cn=an+bn(n>2),问△ABC为何种三角形?为什么?
【答案】令n=3,a=1,b=1,则c=≈1.26,
易观察知△ABC为锐角三角形.
上述特殊值试验的结论具有一般性,下面证明:
因为cn=an+bn(n>2),
所以c>a,c>b,即c是△ABC的最大边.
所以要证△ABC是锐角三角形,
只需证角C为锐角,即证cos C>0.
因为cos C=,
故只需证a2+b2>c2. ①
再注意条件an+bn=cn,于是将①等价变形为
(a2+b2)cn-2>cn(n>2). ②
因为c>a,c>b,n>2,
所以cn-2>an-2,cn-2>bn-2,
即cn-2-an-2>0,cn-2-bn-2>0.
从而(a2+b2)cn-2-cn
=(a2+b2)cn-2-an-bn
=a2(cn-2-an-2)+b2(cn-2-bn-2)>0,
这说明②式成立.
故cos C>0,C是锐角,△ABC为锐角三角形.
19.判断命题“若a>b>c,且a+b+c=0,则<”的真假,并用分析法证明你的结论.
【答案】此命题为真命题,证明过程如下:
∵a+b+c=0,a>b>c,
∴a>0,c<0.
要证<成立,
只需证
只需证(a+c)2-ac<3a2,
即证(a-c)(2a+c)>0,
∵a-c>0,2a+c=(a+c)+a=a-b>0,
∴(a-c)(2a+c)>0成立,故原不等式成立.
20. △ABC的三个内角A、B、C成等差数列, 分别为三个内角A、B、C所对的边,求证: 。
【答案】要证,即需证。
即证。又需证,需证
∵△ABC三个内角A、B、C成等差数列。∴B=60°。
由余弦定理,有,即。
∴成立,命题得证。
21.已知a,b,c为正实数,且a+b+c=1,求证:(-1)(-1)(-1)≥8.
【答案】∵a+b+c=1,且a,b,c为正实数,
∴
=
=
≥2·2·2=8.
22.已知,求证:.
【答案】
要证成立
只需证成立
只需证
只需证
只需证
只需证
只需证
而显然成立,则原不等式得证.
23.已知,且,
(1)求的最小值;
(2)求证:.
【答案】(1)
当且仅当,即时,取到最小值.
(2)
(*)
当且仅当,即,
即,即,
即时,(*)式取到等号.
24.已知:f(x)=x2+px+q.求证:
(1)f(1)+f(3)-2f(2)=2;
(2)|f(1)|,|f(2)|,|f(3)|中至少有一个不小于.
【答案】(1)f(1)+f(3)-2f(2)
=1+p+q+9+3p+q-2(4+2p+q)=2.
(2)反证法:假设|f(1)|,|f(2)|,|f(3)|都小于,
那么2=|f(1)+f(3)-2f(2)|≤|f(1)|+|f(3)|+2|f(2)|<++2·=2矛盾,
所以假设不成立,即|f(1)|,|f(2)|,|f(3)|中至少有一个不小于.
