贵州省兴义七中2012届高考数学二轮复习资料:直线与方程
文档属性
| 名称 | 贵州省兴义七中2012届高考数学二轮复习资料:直线与方程 |

|
|
| 格式 | zip | ||
| 文件大小 | 137.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-17 00:00:00 | ||
图片预览



文档简介
贵州省兴义七中2012届高考数学二轮复习资料:直线与方程
I 卷
一、选择题
1.若直线l:y=kx-与直线2x+3y-6=0交点位于第一象限,则直线l的倾斜角的取值范围是( )
A.,) B.(,) C.(,) D.,)
【答案】B
2.已知点P是抛物线上一点,设P到此抛物线准线的距离是d1,到直线的距离是d2,则dl+d2的最小值是( )
A. B. C. D.3
【答案】C
3. 已知直线 , 与的夹角为( )
A.45° B.60° C.90° D.120°
【答案】B
4. 直线有两个不同交点的一个充分不必要条件是 ( )
A. B. C. D.
【答案】C
5.若过点和的直线与直线平行,则的值为( )
A.6 B. C.2 D.
【答案】B
6. 直线的倾斜角为( )
【答案】A
7. 函数y=asinx-bcosx的一条对称轴为,那么直线:ax-by+c=0的倾斜角为( )
A.450 B.600 C.1200 D.1350
【答案】D
8. 已知直线的倾斜角为300,则直线的斜率值为( ).
A. B. C. D.
【答案】A
9. 如果实数满足条件 ,那么的最大值为
A. B. C. D.
【答案】A
10. 已知,则直线不经过 ( )
A.第1象限 B.第2象限 C.第3象限 D.第4象限
【答案】C
11.已知三条直线和围成一个直角三角形,则的值是( )
A. 或 B.-1或 C.0或-1或 D.0或或
【答案】C
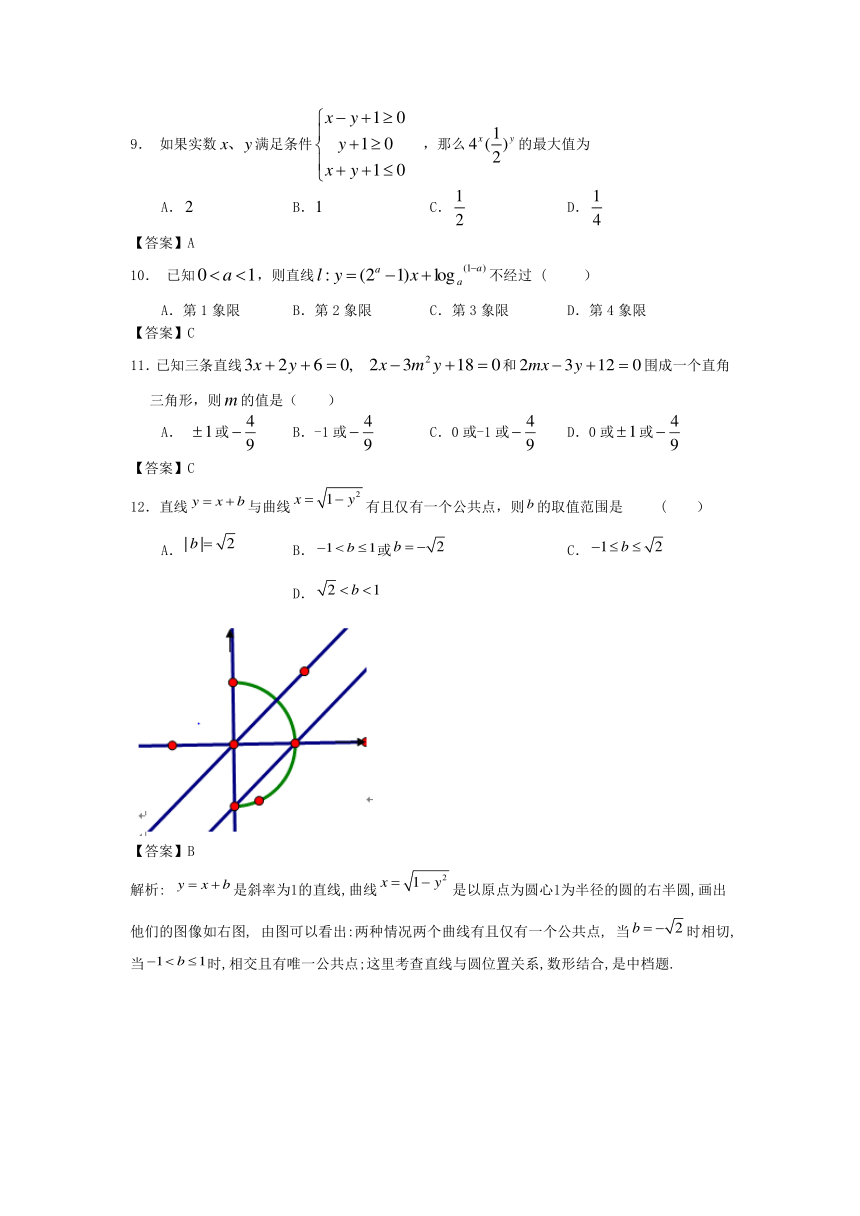
12.直线与曲线有且仅有一个公共点,则的取值范围是 ( )
A. B.或 C. D.
【答案】B
解析: 是斜率为1的直线,曲线是以原点为圆心1为半径的圆的右半圆,画出他们的图像如右图, 由图可以看出:两种情况两个曲线有且仅有一个公共点, 当时相切,当时,相交且有唯一公共点;这里考查直线与圆位置关系,数形结合,是中档题.
II卷
二、填空题
13. 一条光线经点处射向轴上一点B,又从B反射到直线 上的一点C,后又从C点反射回A点,求直线BC的方程。
【答案】 y=-3x+1
14.已知直线l1:y=2x+3,直线l2与l1关于直线y=-x对称,则直线l2的斜率为________.
【答案】
15.设两条直线的方程分别为x+y+a=0,x+y+b=0,已知a,b是方程x2+x+c=0的两个实根,且0≤c≤,则这两条直线之间的距离的最大值和最小值分别是____________.
【答案】,
16.直线x+a2y+1=0与直线(a2+1)x-by+3=0互相垂直,a、b∈R且ab≠0,则|ab|的最小值为________.
【答案】2
三、解答题
17.已知正方形的中点为直线和的交点,正方形一边所在直线的方程为,求其他三边所在直线的方程.
【答案】∴中点坐标为M(-1,0)
点M到直线的距离
设与的直线方程为
∴(舍)或 ∴
设与垂直两线分别为,则(-1,0)到这两条直线距离相等且为,
设方程为
∴ ∴或9 ∴
18. 如图,已知:射线为,射线为,动点在的内部,于,于,四边形的面积恰为.求这个函数的解析式;
【答案】设M(a,a),N(b,-b),(a>0,b>0)。
则|OM|=,|ON|=,
由动点P在∠AOx的内部,得0∴|PM|==,|PN |==
∴(|OM|·|PM|+|ON|·|PN|)
=a(x-y)+b(x+y)=(a+b)x - (a-b)y=
∴ (a+b)x-( a -b)y=2 ①
又由kPM=, kPN=,
分别解得,代入①式消a、b,并化简得x2-y2=4。
∵y>0,∴
19. 如图,一列载着危重病人的火车从O地出发,沿射线OA方向行驶,其中,在距离O地5a(a为正常数)千米,北偏东角的N处住有一位医学专家,其中,现120指挥中心紧急征调离O地正东p千米B处的救护车,先到N处载上医学专家,再全速赶往乘有危重病人的火车,并在C处相遇。经计算,当两车行驶的路线与OB所围成的三角形OBC面积S最小时,抢救最及时。
(1)在以O为原点,正北方向为y轴的直角坐标系中,求射线OA所在的直线方程;
(2)求S关于p的函数关系式S=;
(3)当p为何值时,抢救最及时?
【答案】(1)由得,∴直线OA的方程为y=3x.
(2)设点N(),则,∴N( 又B(),∴直线BC的方程为.由得C的纵坐标,∴三角形OBC面积.
(3)由(2)知.∵,∴∴时,.因此,当千米时,抢救最及时.
20.已知点,在直线上求一点P,使最小.
【答案】由题意知,点A、B在直线的同一侧.由平面几何性质可知,先作出点关于直线的对称点,然后连结,则直线与的交点P为所求.事实上,设点是上异于P的点,则.
设,则,解得,∴,∴直线的方程为.由,解得,∴.
21.已知两直线.试确定的值,使
(1);
(2),且在轴上的截距为.
【答案】(1)当m=0时,显然l1与l2不平行.
当m≠0时,由=≠得
m·m-8×2=0,得m=±4,
8×(-1)-n·m≠0,得n≠±2,
即m=4,n≠-2时,或m=-4,n≠2时,l1∥l2.
(2)当且仅当m·2+8·m=0,即m=0时,l1⊥l2.
又-=-1,∴n=8.
即m=0,n=8时,l1⊥l2,且l1在y轴上的截距为-1.
22.已知两直线,求分别满足下列条件的、的值.
(1)直线过点,并且直线与直线垂直;
(2)直线与直线平行,并且坐标原点到、的距离相等.
【答案】(1)
即 ①
又点在上, ②
由①②解得:
(2)∥且的斜率为. ∴的斜率也存在,即,.
故和的方程可分别表示为:
∵原点到和的距离相等. ∴,解得:或.
因此或.
23.已知点A(1,4),B(6,2),试问在直线x-3y+3=0上是否存在点C,使得三角形ABC的面积等于14?若存在,求出C点坐标;若不存在,说明理由。
【答案】AB=,直线AB的方程为,即,假设在直线x-3y+3=0上是否存在点C,使得三角形ABC的面积等于14,设C的坐标为,则一方面有m-3n+3=0①,另一方面点C到直线AB的距离为,由于三角形ABC的面积等于14,则,,即②或③.联立①②解得,;联立①③解得,.综上,在直线x-3y+3=0上存在点C或,使得三角形ABC的面积等于14.
24. 过点作一直线l,使它与两坐标轴相交且与两轴所围成的三角形面积为5.求此直线的方程。
【答案】直线l的方程为,
令 得;令得
解得或
所求方程为或
I 卷
一、选择题
1.若直线l:y=kx-与直线2x+3y-6=0交点位于第一象限,则直线l的倾斜角的取值范围是( )
A.,) B.(,) C.(,) D.,)
【答案】B
2.已知点P是抛物线上一点,设P到此抛物线准线的距离是d1,到直线的距离是d2,则dl+d2的最小值是( )
A. B. C. D.3
【答案】C
3. 已知直线 , 与的夹角为( )
A.45° B.60° C.90° D.120°
【答案】B
4. 直线有两个不同交点的一个充分不必要条件是 ( )
A. B. C. D.
【答案】C
5.若过点和的直线与直线平行,则的值为( )
A.6 B. C.2 D.
【答案】B
6. 直线的倾斜角为( )
【答案】A
7. 函数y=asinx-bcosx的一条对称轴为,那么直线:ax-by+c=0的倾斜角为( )
A.450 B.600 C.1200 D.1350
【答案】D
8. 已知直线的倾斜角为300,则直线的斜率值为( ).
A. B. C. D.
【答案】A
9. 如果实数满足条件 ,那么的最大值为
A. B. C. D.
【答案】A
10. 已知,则直线不经过 ( )
A.第1象限 B.第2象限 C.第3象限 D.第4象限
【答案】C
11.已知三条直线和围成一个直角三角形,则的值是( )
A. 或 B.-1或 C.0或-1或 D.0或或
【答案】C
12.直线与曲线有且仅有一个公共点,则的取值范围是 ( )
A. B.或 C. D.
【答案】B
解析: 是斜率为1的直线,曲线是以原点为圆心1为半径的圆的右半圆,画出他们的图像如右图, 由图可以看出:两种情况两个曲线有且仅有一个公共点, 当时相切,当时,相交且有唯一公共点;这里考查直线与圆位置关系,数形结合,是中档题.
II卷
二、填空题
13. 一条光线经点处射向轴上一点B,又从B反射到直线 上的一点C,后又从C点反射回A点,求直线BC的方程。
【答案】 y=-3x+1
14.已知直线l1:y=2x+3,直线l2与l1关于直线y=-x对称,则直线l2的斜率为________.
【答案】
15.设两条直线的方程分别为x+y+a=0,x+y+b=0,已知a,b是方程x2+x+c=0的两个实根,且0≤c≤,则这两条直线之间的距离的最大值和最小值分别是____________.
【答案】,
16.直线x+a2y+1=0与直线(a2+1)x-by+3=0互相垂直,a、b∈R且ab≠0,则|ab|的最小值为________.
【答案】2
三、解答题
17.已知正方形的中点为直线和的交点,正方形一边所在直线的方程为,求其他三边所在直线的方程.
【答案】∴中点坐标为M(-1,0)
点M到直线的距离
设与的直线方程为
∴(舍)或 ∴
设与垂直两线分别为,则(-1,0)到这两条直线距离相等且为,
设方程为
∴ ∴或9 ∴
18. 如图,已知:射线为,射线为,动点在的内部,于,于,四边形的面积恰为.求这个函数的解析式;
【答案】设M(a,a),N(b,-b),(a>0,b>0)。
则|OM|=,|ON|=,
由动点P在∠AOx的内部,得0
∴(|OM|·|PM|+|ON|·|PN|)
=a(x-y)+b(x+y)=(a+b)x - (a-b)y=
∴ (a+b)x-( a -b)y=2 ①
又由kPM=, kPN=,
分别解得,代入①式消a、b,并化简得x2-y2=4。
∵y>0,∴
19. 如图,一列载着危重病人的火车从O地出发,沿射线OA方向行驶,其中,在距离O地5a(a为正常数)千米,北偏东角的N处住有一位医学专家,其中,现120指挥中心紧急征调离O地正东p千米B处的救护车,先到N处载上医学专家,再全速赶往乘有危重病人的火车,并在C处相遇。经计算,当两车行驶的路线与OB所围成的三角形OBC面积S最小时,抢救最及时。
(1)在以O为原点,正北方向为y轴的直角坐标系中,求射线OA所在的直线方程;
(2)求S关于p的函数关系式S=;
(3)当p为何值时,抢救最及时?
【答案】(1)由得,∴直线OA的方程为y=3x.
(2)设点N(),则,∴N( 又B(),∴直线BC的方程为.由得C的纵坐标,∴三角形OBC面积.
(3)由(2)知.∵,∴∴时,.因此,当千米时,抢救最及时.
20.已知点,在直线上求一点P,使最小.
【答案】由题意知,点A、B在直线的同一侧.由平面几何性质可知,先作出点关于直线的对称点,然后连结,则直线与的交点P为所求.事实上,设点是上异于P的点,则.
设,则,解得,∴,∴直线的方程为.由,解得,∴.
21.已知两直线.试确定的值,使
(1);
(2),且在轴上的截距为.
【答案】(1)当m=0时,显然l1与l2不平行.
当m≠0时,由=≠得
m·m-8×2=0,得m=±4,
8×(-1)-n·m≠0,得n≠±2,
即m=4,n≠-2时,或m=-4,n≠2时,l1∥l2.
(2)当且仅当m·2+8·m=0,即m=0时,l1⊥l2.
又-=-1,∴n=8.
即m=0,n=8时,l1⊥l2,且l1在y轴上的截距为-1.
22.已知两直线,求分别满足下列条件的、的值.
(1)直线过点,并且直线与直线垂直;
(2)直线与直线平行,并且坐标原点到、的距离相等.
【答案】(1)
即 ①
又点在上, ②
由①②解得:
(2)∥且的斜率为. ∴的斜率也存在,即,.
故和的方程可分别表示为:
∵原点到和的距离相等. ∴,解得:或.
因此或.
23.已知点A(1,4),B(6,2),试问在直线x-3y+3=0上是否存在点C,使得三角形ABC的面积等于14?若存在,求出C点坐标;若不存在,说明理由。
【答案】AB=,直线AB的方程为,即,假设在直线x-3y+3=0上是否存在点C,使得三角形ABC的面积等于14,设C的坐标为,则一方面有m-3n+3=0①,另一方面点C到直线AB的距离为,由于三角形ABC的面积等于14,则,,即②或③.联立①②解得,;联立①③解得,.综上,在直线x-3y+3=0上存在点C或,使得三角形ABC的面积等于14.
24. 过点作一直线l,使它与两坐标轴相交且与两轴所围成的三角形面积为5.求此直线的方程。
【答案】直线l的方程为,
令 得;令得
解得或
所求方程为或
