重庆市西南大学附高2020-2021学年高一下学期6月月考数学试题(2021.6.27) Word版含答案
文档属性
| 名称 | 重庆市西南大学附高2020-2021学年高一下学期6月月考数学试题(2021.6.27) Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 492.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 18:51:24 | ||
图片预览




文档简介
西南大学附属中学2020-2021学年高一下学期6月月考
数学(6.27)
单选题(本大题共8小题,共40分)
1.已知复数false,则false的虚部为( )
A.false B.false C.false D.false
2.如果平面向量false,false,那么下列结论中不正确的是( )
A.false
B.false
C.false,false的夹角为180°
D.向量false在false方向上的投影为false
3.设false,p:向量false与false的夹角为钝角,q:false,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.在false中,内角false,false,false的对边分别为false,false,false,若false的面积为false,且false,false,则false外接圆的半径为( )
A.2 B.false C.1 D.false
5.已知向量false,false,则false的面积为( ).
A.1 B.2 C.3 D.4
6.正方体的内切球和外接球的体积之比为( )
A.false B.false C.false D.false
7.已知直线false和平面false,则下列结论一定成立的是( )
A.若false,则false B.若false,false,则false
C.若false,false,则false D.若false,false,则false
8.正三棱锥的底面周长为false,侧面都是直角三角形,则此棱锥的体积为( )
A.false B.false C.false D.false
二、多选题(本大题共4小题,共20分)
9.给出以下结论:正确的为( )
A.直线false平面false,直线false,则false B.若false,则false
C.若false,则false或a与false相交 D.若false,false,则a、b无公共点
10.下列命题是真命题的有( )
A.有甲、乙、丙三种个体按false的比例分层抽样调查,如果抽取的甲个体数为9,则样本容量为30
B.数据1,2,3,3,4,5的平均数、众数、中位数相同
C.若甲组数据的方差为5,乙组数据为5,6,9,10,5,则这两组数据中较稳定的是乙
D.一组数6,5,4,3,3,3,2,2,2,1的85%分位数为5
11.下列结论正确的是( )
A.已知false是非零向量,false,若false,则false
B.非零向量false和false,满足false,则false与false的夹角为false
C.点false在false所在的平面内,满足false,则点false是false的外心
D.以false为顶点的四边形是一个矩形
12.如图,在底面为正方形的四棱锥false中,false平面false,false,则( )
A.异面直线false,false所成的角为false
B.三棱锥false的体积为false
C.直线false与平面false所成的角为false
D.平面false与平面false所成的角为false
三、填空题(本大题共4小题,共20分)
13.若复数false与它的共轭复数false所对应的向量互相垂直,则false_______.
14.记false的内角A,B,C的对边分别为a,b,c,面积为false,false,false,则false________.
15.已知一个圆锥的底面半径为6,其体积为false则该圆锥的侧面积为________.
16.在如图所示四边形false中,false,false,false,false,false,则四边形false的面积为________.
四、解答题(本大题共20分)
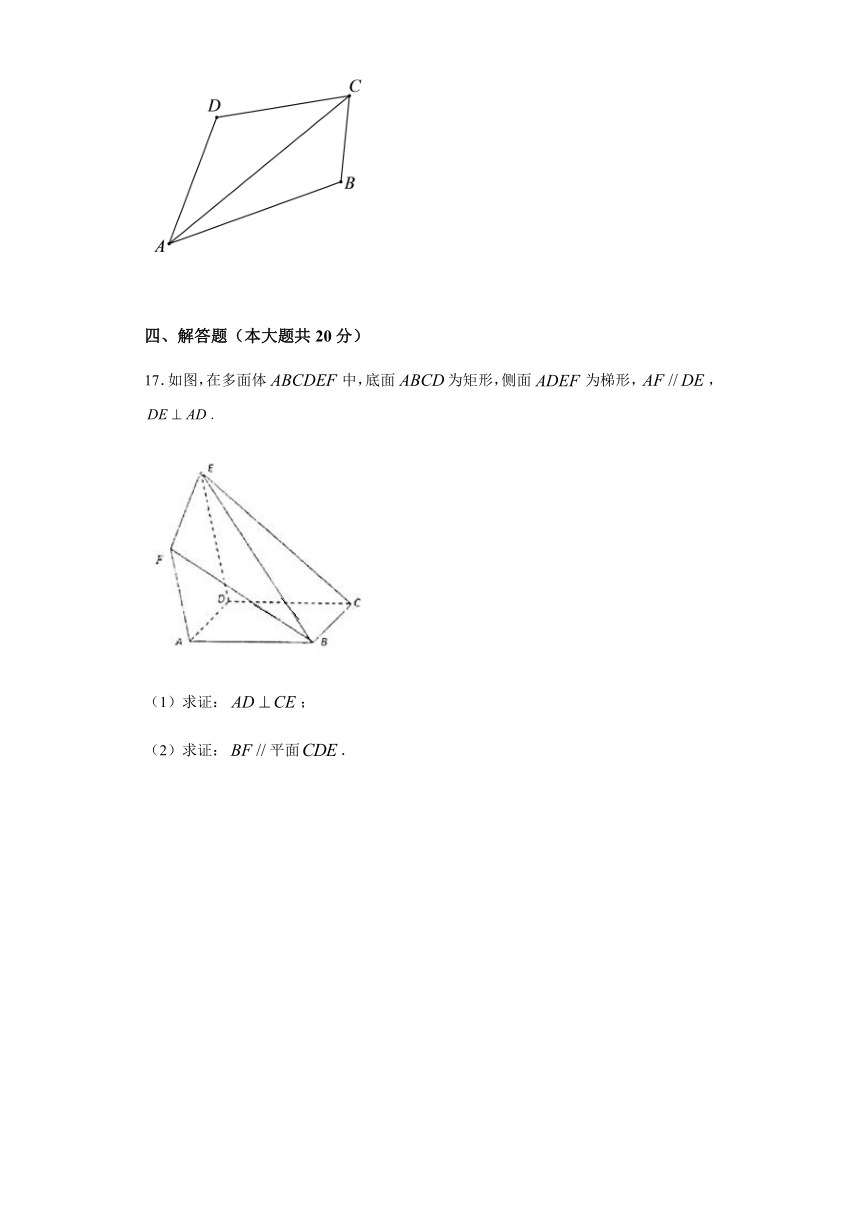
17.如图,在多面体false中,底面false为矩形,侧面false为梯形,false,false.
(1)求证:false;
(2)求证:false平面false.
西南大学附属中学2020-2021学年高一下学期6月月考
数学(大6.27)参考答案
1.C
【分析】
根据复数的除法运算法则化简,再由虚部的定义求解即可.
【详解】
false复数false
所以false的虚部为false,
故选:C.
2.D
【分析】
直接利用向量的坐标运算,向量的模,向量的夹角运算,向量在另一个向量上的投影的应用判定选项的结论.
【详解】
解:因为false,false,所以false,
对于A,因为false,所以false,故A正确;
对于B,因为false,故false,故B正确;
对于C,因为false,所以false与false的夹角为180°,故C正确;
对于D,false在false方向上的投影为:false,false,故D错误.
故选:D.
3.A
【分析】
由题知false,进而根据题意得以false且false与false的不共线,解得false且false,再结合集合关系判断即可得答案.
【详解】
由题知false,
因为向量false与false的夹角为钝角,
所以false且false与false的不共线,
所以false且false,解得false且false
因为false是false的真子集,
所以p是q的充分不必要条件,
故选:A
【点睛】
结论点睛:本题考查充分不必要条件的判断,一般可根据如下规则判断:
(1)若false是false的必要不充分条件,则false对应集合是false对应集合的真子集;
(2)false是false的充分不必要条件, 则false对应集合是false对应集合的真子集;
(3)false是false的充分必要条件,则false对应集合与false对应集合相等;
(4)false是false的既不充分又不必要条件, false对的集合与false对应集合互不包含.
4.D
【分析】
由三角形的面积公式和余弦定理结合已知条件可求出角false,再利用正弦定理可求得结果
【详解】
解:因为false,所以false,
因为false,false,
所以false,所以false,
因为false,所以false,
因为false,所以false,
设false外接圆的半径为false
则由正弦定理得false,得false,
故选:D
5.A
【分析】
利用向量运算求得false,由此求得false,利用三角形的面积公式求得三角形false的面积.
【详解】
false,
false,
false,所以false,
所以false.
故选:A
6.A
【分析】
本题可设正方体的棱长为false,然后求出内切球的体积false,最后求出外接球的体积false,即可得出结果.
7.C
【分析】
利用特例排除法,容易否定ABD,利用线面、面面垂直、平行的的关系可以断定C正确.
【详解】
选项A中,也可能false;选项B中,false也有可能在false内;选项D中,m与false的关系不确定,故可排除A,B,D.由线面平行和垂直的判定与性质可以看出C正确.
故选C.
8.D
【分析】
本题首先可根据题意求出侧棱长均为false,然后根据三条侧棱两两垂直即可求出棱锥的体积.
【详解】
因为正三棱锥的底面周长为false,所以正三棱锥的底面边长为false,
因为侧面都是直角三角形,所以侧棱长均为false,
因为三条侧棱两两垂直,所以此棱锥的体积false,
故选:D.
9.BC
【分析】
根据线线、线面关系一一分析即可.
【详解】
对于A,直线false平面false,直线false,则a与b 的关系可以平行或者异面,故A错误;
对于B,若false,则a与平面false只有一个交点,即相交,false,故B正确;
对于C,若false,则false或a与false相交,故C正确;
对于D,若false,false,则b与平面false可以相交且与a相交,故D错误;
故选:BC
10.BCD
【分析】
根据分层抽样的性质判断A;计算出平均数、中位数、众数判断B;计算乙的方差判断C;由百分位数的性质判断D.
【详解】
对于A项,乙、丙抽取的个体数分别为false,则样本容量为false,故A错误;
对于B项,平均数为false,中位数为false,众数为false,故B正确;
对于C项,乙的平均数为false,方差为false,则这两组数据中较稳定的是乙,故C正确;
对于D项,将该组数据总小到大排列false,由false,则该组数据的85%分位数为5,故D正确;
故选:BCD
11.ABD
【分析】
对A,由向量垂直的的运算法则可判断正确;
对B,可结合线性运算作图快速判断正确;
对C,结合重心性质可判断当false时,应为三角形中心,判断错误;
对D,可设false,可证false,可判断四边形为平行四边形,再证false即可判断四边形为矩形
【详解】
对A,false是非零向量,false,若false,即false,false,
即false,故A正确;
对B,由非零向量false和false,满足false,如图所示:
当向量false方向如图所示,夹角为120°时,刚好满足题设条件,
则false为菱形的斜对角线所示方向,
false与false的夹角为刚好为菱形锐角夹角的一半,故为false,故B正确;
对C,当false时,false点为false的重心,故C错误;
对D,可设false,则false,
false,则四边形false为平行四边形,又false,
故false,根据有一个角为90°的平行四边形为矩形可判断四边形false为矩形,
故D正确.
故答案为:ABD.
【点睛】
本题考查平线向量的综合应用,向量垂直的判断,向量在几何关系中的应用问题,属于中档题
12.ABC
【分析】
取PD中点E并过E作PB的平行线得异面直线PB,AC夹角,再计算并判断A;用等体积法转化计算并判断B;证BD⊥平面PAC得线面角再计算并判断C;作出二面角A-PB-D的平面角,再计算并判断D.
【详解】
四棱锥false的底面为正方形,令false,则O是BD,AC的中点,如图:
取PD中点E,连OE,则false,异面直线false,false所成的角为false或其补角,
因false平面false,false,则false,false,A正确;
三棱锥false的体积false,B正确;
连PO,因BD⊥AC,而BD⊥PA,即BD⊥平面PAC,PO是PD在平面PAC内射影,即false是直线PD现平面PAC所成角,
false,即false,C正确;
取PB中点F,连AF,DF,则AF⊥PB,而false,则DF⊥PB,即false是二面角A-PB-D的平面角,
false,false不等于false,即D不正确.
故选:ABC
【点睛】
思路点睛:作二面角的平面角可以通过垂线法进行,在一个半平面内找一点作另一个半平面的垂线,再过垂足作二面角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角.
13.false
【分析】
利用数量积为false列方程,解方程求得false.
【详解】
false对应坐标为false,
false对应坐标为false,
依题意false,
解得false.
故答案为:false
14.false
【分析】
由三角形面积公式可得false,再结合余弦定理即可得解.
【详解】
由题意,false,
所以false,
所以false,解得false(负值舍去).
故答案为:false.
15.false
【分析】
利用体积公式求出圆锥的高,进一步求出母线长,最终利用侧面积公式求出答案.
【详解】
∵false
∴false
∴false
∴false.
故答案为:false.
16.false
【分析】
由已知条件可得false,false,false,应用三角形面积公式求false,false,即可求四边形false的面积.
【详解】
由题意,知:false,且false,false,
∴false,false,
∴四边形false的面积false.
故答案为:false
17.(1)见解析;(2)见解析.
【分析】
(1)易证AD⊥平面CDE,从而AD⊥CE;(2)先证平面ABF∥平面CDE,可得BF∥平面CDE.
【详解】
证明:(1)因为矩形ABCD
所以AD⊥CD
又因为DE⊥AD,且CDfalseDE=D,CD、DEfalse平面CDE
所以AD⊥平面CDE
又因为CEfalse平面CDE
所以AD⊥CE
(2)因为AB∥CD,CDfalse平面CDE,AB false平面CDE
所以AB∥平面CDE
又因为AF∥DE,DEfalse平面CDE,AFfalse 平面CDE
所以AF∥平面CDE
又因为ABfalseAF=A,AB、AFfalse平面ABF
所以平面ABF∥平面CDE
又因为BFfalse平面ABF
所以BF∥平面CDE
【点睛】
本题考查了异面直线垂直的证明和线面平行的证明,异面直线垂直常先证线面垂直,线面平行证明可用其判定定理,也可先证面面平行再得线面平行.
数学(6.27)
单选题(本大题共8小题,共40分)
1.已知复数false,则false的虚部为( )
A.false B.false C.false D.false
2.如果平面向量false,false,那么下列结论中不正确的是( )
A.false
B.false
C.false,false的夹角为180°
D.向量false在false方向上的投影为false
3.设false,p:向量false与false的夹角为钝角,q:false,则p是q的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.在false中,内角false,false,false的对边分别为false,false,false,若false的面积为false,且false,false,则false外接圆的半径为( )
A.2 B.false C.1 D.false
5.已知向量false,false,则false的面积为( ).
A.1 B.2 C.3 D.4
6.正方体的内切球和外接球的体积之比为( )
A.false B.false C.false D.false
7.已知直线false和平面false,则下列结论一定成立的是( )
A.若false,则false B.若false,false,则false
C.若false,false,则false D.若false,false,则false
8.正三棱锥的底面周长为false,侧面都是直角三角形,则此棱锥的体积为( )
A.false B.false C.false D.false
二、多选题(本大题共4小题,共20分)
9.给出以下结论:正确的为( )
A.直线false平面false,直线false,则false B.若false,则false
C.若false,则false或a与false相交 D.若false,false,则a、b无公共点
10.下列命题是真命题的有( )
A.有甲、乙、丙三种个体按false的比例分层抽样调查,如果抽取的甲个体数为9,则样本容量为30
B.数据1,2,3,3,4,5的平均数、众数、中位数相同
C.若甲组数据的方差为5,乙组数据为5,6,9,10,5,则这两组数据中较稳定的是乙
D.一组数6,5,4,3,3,3,2,2,2,1的85%分位数为5
11.下列结论正确的是( )
A.已知false是非零向量,false,若false,则false
B.非零向量false和false,满足false,则false与false的夹角为false
C.点false在false所在的平面内,满足false,则点false是false的外心
D.以false为顶点的四边形是一个矩形
12.如图,在底面为正方形的四棱锥false中,false平面false,false,则( )
A.异面直线false,false所成的角为false
B.三棱锥false的体积为false
C.直线false与平面false所成的角为false
D.平面false与平面false所成的角为false
三、填空题(本大题共4小题,共20分)
13.若复数false与它的共轭复数false所对应的向量互相垂直,则false_______.
14.记false的内角A,B,C的对边分别为a,b,c,面积为false,false,false,则false________.
15.已知一个圆锥的底面半径为6,其体积为false则该圆锥的侧面积为________.
16.在如图所示四边形false中,false,false,false,false,false,则四边形false的面积为________.
四、解答题(本大题共20分)
17.如图,在多面体false中,底面false为矩形,侧面false为梯形,false,false.
(1)求证:false;
(2)求证:false平面false.
西南大学附属中学2020-2021学年高一下学期6月月考
数学(大6.27)参考答案
1.C
【分析】
根据复数的除法运算法则化简,再由虚部的定义求解即可.
【详解】
false复数false
所以false的虚部为false,
故选:C.
2.D
【分析】
直接利用向量的坐标运算,向量的模,向量的夹角运算,向量在另一个向量上的投影的应用判定选项的结论.
【详解】
解:因为false,false,所以false,
对于A,因为false,所以false,故A正确;
对于B,因为false,故false,故B正确;
对于C,因为false,所以false与false的夹角为180°,故C正确;
对于D,false在false方向上的投影为:false,false,故D错误.
故选:D.
3.A
【分析】
由题知false,进而根据题意得以false且false与false的不共线,解得false且false,再结合集合关系判断即可得答案.
【详解】
由题知false,
因为向量false与false的夹角为钝角,
所以false且false与false的不共线,
所以false且false,解得false且false
因为false是false的真子集,
所以p是q的充分不必要条件,
故选:A
【点睛】
结论点睛:本题考查充分不必要条件的判断,一般可根据如下规则判断:
(1)若false是false的必要不充分条件,则false对应集合是false对应集合的真子集;
(2)false是false的充分不必要条件, 则false对应集合是false对应集合的真子集;
(3)false是false的充分必要条件,则false对应集合与false对应集合相等;
(4)false是false的既不充分又不必要条件, false对的集合与false对应集合互不包含.
4.D
【分析】
由三角形的面积公式和余弦定理结合已知条件可求出角false,再利用正弦定理可求得结果
【详解】
解:因为false,所以false,
因为false,false,
所以false,所以false,
因为false,所以false,
因为false,所以false,
设false外接圆的半径为false
则由正弦定理得false,得false,
故选:D
5.A
【分析】
利用向量运算求得false,由此求得false,利用三角形的面积公式求得三角形false的面积.
【详解】
false,
false,
false,所以false,
所以false.
故选:A
6.A
【分析】
本题可设正方体的棱长为false,然后求出内切球的体积false,最后求出外接球的体积false,即可得出结果.
7.C
【分析】
利用特例排除法,容易否定ABD,利用线面、面面垂直、平行的的关系可以断定C正确.
【详解】
选项A中,也可能false;选项B中,false也有可能在false内;选项D中,m与false的关系不确定,故可排除A,B,D.由线面平行和垂直的判定与性质可以看出C正确.
故选C.
8.D
【分析】
本题首先可根据题意求出侧棱长均为false,然后根据三条侧棱两两垂直即可求出棱锥的体积.
【详解】
因为正三棱锥的底面周长为false,所以正三棱锥的底面边长为false,
因为侧面都是直角三角形,所以侧棱长均为false,
因为三条侧棱两两垂直,所以此棱锥的体积false,
故选:D.
9.BC
【分析】
根据线线、线面关系一一分析即可.
【详解】
对于A,直线false平面false,直线false,则a与b 的关系可以平行或者异面,故A错误;
对于B,若false,则a与平面false只有一个交点,即相交,false,故B正确;
对于C,若false,则false或a与false相交,故C正确;
对于D,若false,false,则b与平面false可以相交且与a相交,故D错误;
故选:BC
10.BCD
【分析】
根据分层抽样的性质判断A;计算出平均数、中位数、众数判断B;计算乙的方差判断C;由百分位数的性质判断D.
【详解】
对于A项,乙、丙抽取的个体数分别为false,则样本容量为false,故A错误;
对于B项,平均数为false,中位数为false,众数为false,故B正确;
对于C项,乙的平均数为false,方差为false,则这两组数据中较稳定的是乙,故C正确;
对于D项,将该组数据总小到大排列false,由false,则该组数据的85%分位数为5,故D正确;
故选:BCD
11.ABD
【分析】
对A,由向量垂直的的运算法则可判断正确;
对B,可结合线性运算作图快速判断正确;
对C,结合重心性质可判断当false时,应为三角形中心,判断错误;
对D,可设false,可证false,可判断四边形为平行四边形,再证false即可判断四边形为矩形
【详解】
对A,false是非零向量,false,若false,即false,false,
即false,故A正确;
对B,由非零向量false和false,满足false,如图所示:
当向量false方向如图所示,夹角为120°时,刚好满足题设条件,
则false为菱形的斜对角线所示方向,
false与false的夹角为刚好为菱形锐角夹角的一半,故为false,故B正确;
对C,当false时,false点为false的重心,故C错误;
对D,可设false,则false,
false,则四边形false为平行四边形,又false,
故false,根据有一个角为90°的平行四边形为矩形可判断四边形false为矩形,
故D正确.
故答案为:ABD.
【点睛】
本题考查平线向量的综合应用,向量垂直的判断,向量在几何关系中的应用问题,属于中档题
12.ABC
【分析】
取PD中点E并过E作PB的平行线得异面直线PB,AC夹角,再计算并判断A;用等体积法转化计算并判断B;证BD⊥平面PAC得线面角再计算并判断C;作出二面角A-PB-D的平面角,再计算并判断D.
【详解】
四棱锥false的底面为正方形,令false,则O是BD,AC的中点,如图:
取PD中点E,连OE,则false,异面直线false,false所成的角为false或其补角,
因false平面false,false,则false,false,A正确;
三棱锥false的体积false,B正确;
连PO,因BD⊥AC,而BD⊥PA,即BD⊥平面PAC,PO是PD在平面PAC内射影,即false是直线PD现平面PAC所成角,
false,即false,C正确;
取PB中点F,连AF,DF,则AF⊥PB,而false,则DF⊥PB,即false是二面角A-PB-D的平面角,
false,false不等于false,即D不正确.
故选:ABC
【点睛】
思路点睛:作二面角的平面角可以通过垂线法进行,在一个半平面内找一点作另一个半平面的垂线,再过垂足作二面角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角.
13.false
【分析】
利用数量积为false列方程,解方程求得false.
【详解】
false对应坐标为false,
false对应坐标为false,
依题意false,
解得false.
故答案为:false
14.false
【分析】
由三角形面积公式可得false,再结合余弦定理即可得解.
【详解】
由题意,false,
所以false,
所以false,解得false(负值舍去).
故答案为:false.
15.false
【分析】
利用体积公式求出圆锥的高,进一步求出母线长,最终利用侧面积公式求出答案.
【详解】
∵false
∴false
∴false
∴false.
故答案为:false.
16.false
【分析】
由已知条件可得false,false,false,应用三角形面积公式求false,false,即可求四边形false的面积.
【详解】
由题意,知:false,且false,false,
∴false,false,
∴四边形false的面积false.
故答案为:false
17.(1)见解析;(2)见解析.
【分析】
(1)易证AD⊥平面CDE,从而AD⊥CE;(2)先证平面ABF∥平面CDE,可得BF∥平面CDE.
【详解】
证明:(1)因为矩形ABCD
所以AD⊥CD
又因为DE⊥AD,且CDfalseDE=D,CD、DEfalse平面CDE
所以AD⊥平面CDE
又因为CEfalse平面CDE
所以AD⊥CE
(2)因为AB∥CD,CDfalse平面CDE,AB false平面CDE
所以AB∥平面CDE
又因为AF∥DE,DEfalse平面CDE,AFfalse 平面CDE
所以AF∥平面CDE
又因为ABfalseAF=A,AB、AFfalse平面ABF
所以平面ABF∥平面CDE
又因为BFfalse平面ABF
所以BF∥平面CDE
【点睛】
本题考查了异面直线垂直的证明和线面平行的证明,异面直线垂直常先证线面垂直,线面平行证明可用其判定定理,也可先证面面平行再得线面平行.
同课章节目录
