2021-2022学年人教版数学八上同步检测附答案11.2.1 三角形的内角第1课时 三角形的内角(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八上同步检测附答案11.2.1 三角形的内角第1课时 三角形的内角(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 239.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 17:37:46 | ||
图片预览

文档简介
11.2.1
三角形的内角第1课时
三角形的内角
一、选择题(共8小题;共40分)
1.
在
中,,,则
的形状是
A.
等边三角形
B.
锐角三角形
C.
直角三角形
D.
钝角三角形
2.
下列各组角的度数中,哪一组是同一个三角形的内角度数
A.
,,
B.
,,
C.
,,
D.
,,
3.
在
中,,,则
的度数为
A.
B.
C.
D.
4.
如图是一块三角形木板的残余部分,量得
,,这块三角形木板另外一个角的度数为
A.
B.
C.
D.
5.
如图,直线
,,,则
的大小是
A.
B.
C.
D.
6.
已知在
中,
是
的
倍,
比
大
,则
的度数为
A.
B.
C.
D.
7.
如图,在
中,,,
平分
交
于点
,
交
于点
,则
的大小是
A.
B.
C.
D.
8.
上午
时,一艘船从
处出发以每小时
海里的速度向正北航行,
时到达
处,若在
处测得灯塔
在北偏西
方向,且
,则在
处测得灯塔
应在
A.
南偏西
方向
B.
北偏西
方向
C.
南偏西
方向
D.
北偏西
方向
二、填空题(共4小题;共20分)
9.
在
中,,,则
?.
10.
一个三角形三个内角的度数之比是
,那么这个三角形是
?
三角形.
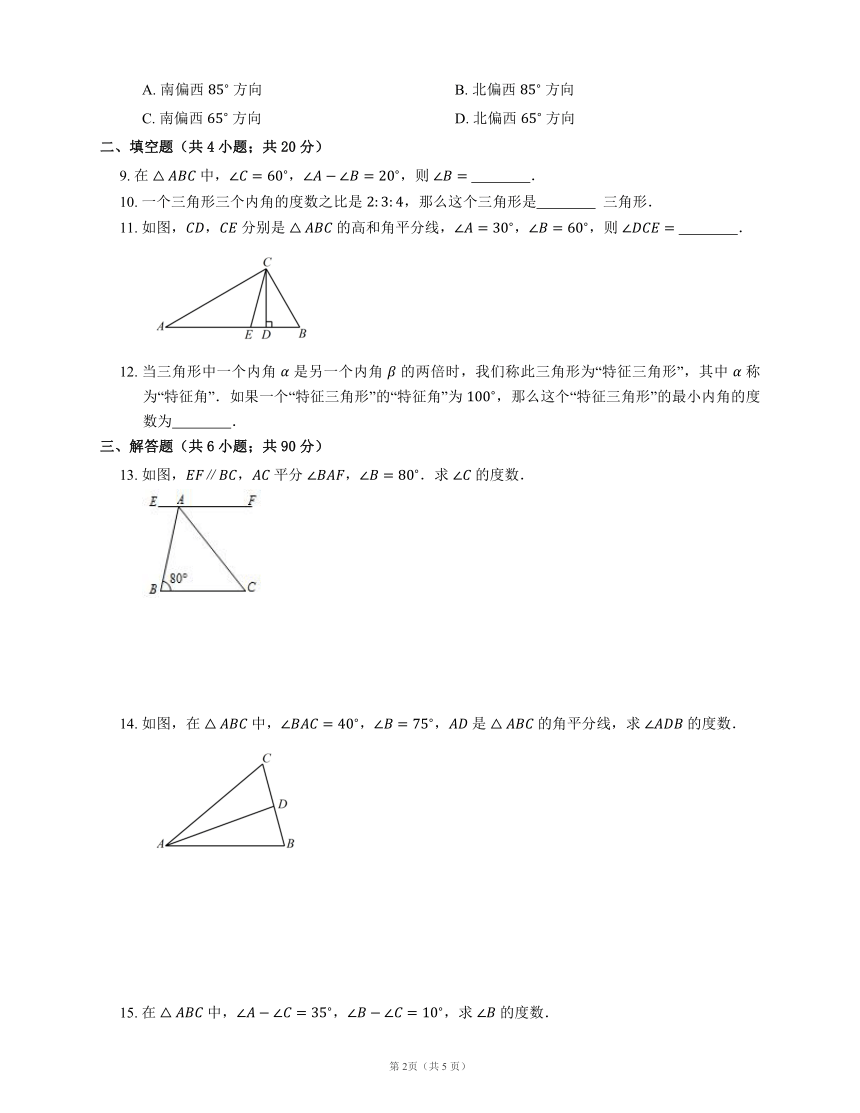
11.
如图,,
分别是
的高和角平分线,,,则
?.
12.
当三角形中一个内角
是另一个内角
的两倍时,我们称此三角形为“特征三角形”,其中
称为“特征角”.如果一个“特征三角形”的“特征角”为
,那么这个“特征三角形”的最小内角的度数为
?.
三、解答题(共6小题;共90分)
13.
如图,,
平分
,.求
的度数.
14.
如图,在
中,,,
是
的角平分线,求
的度数.
15.
在
中,,,求
的度数.
16.
如图,在
中,,
分别是
和
的平分线,已知
,求
的度数.
17.
如图,
的内角度数之比为
,
是
的平分线,求
的度数.
18.
如图所示,将
沿
折叠,使点
落在点
处,试探求
,
与
的数量关系.
答案
1.
D
【解析】由题意得
,
故
是钝角三角形.
2.
A
3.
C
4.
B
5.
C
6.
A
7.
C
8.
B
9.
10.
锐角
11.
12.
【解析】根据“特征三角形”和“特征角”的定义可知,如果一个“特征三角形”的“特征角”为
,则另一个内角为
,根据三角形的内角和定理求出第
个角为
,所以这个“特征三角形”的最小内角的度数为
.
13.
,
.
平分
,
,
,
.
14.
是
的角平分线,
.
.
,
.
15.
,
.
,
.
又
,
.
16.
,
.
,
分别是
和
的平分线,
.
.
17.
设
,,
,
.
,
.
是
的平分线,
,
,
.
18.
根据三角形内角和
,知
.
由于折叠,所以
,
.
,
,
.
.
第1页(共5
页)
三角形的内角第1课时
三角形的内角
一、选择题(共8小题;共40分)
1.
在
中,,,则
的形状是
A.
等边三角形
B.
锐角三角形
C.
直角三角形
D.
钝角三角形
2.
下列各组角的度数中,哪一组是同一个三角形的内角度数
A.
,,
B.
,,
C.
,,
D.
,,
3.
在
中,,,则
的度数为
A.
B.
C.
D.
4.
如图是一块三角形木板的残余部分,量得
,,这块三角形木板另外一个角的度数为
A.
B.
C.
D.
5.
如图,直线
,,,则
的大小是
A.
B.
C.
D.
6.
已知在
中,
是
的
倍,
比
大
,则
的度数为
A.
B.
C.
D.
7.
如图,在
中,,,
平分
交
于点
,
交
于点
,则
的大小是
A.
B.
C.
D.
8.
上午
时,一艘船从
处出发以每小时
海里的速度向正北航行,
时到达
处,若在
处测得灯塔
在北偏西
方向,且
,则在
处测得灯塔
应在
A.
南偏西
方向
B.
北偏西
方向
C.
南偏西
方向
D.
北偏西
方向
二、填空题(共4小题;共20分)
9.
在
中,,,则
?.
10.
一个三角形三个内角的度数之比是
,那么这个三角形是
?
三角形.
11.
如图,,
分别是
的高和角平分线,,,则
?.
12.
当三角形中一个内角
是另一个内角
的两倍时,我们称此三角形为“特征三角形”,其中
称为“特征角”.如果一个“特征三角形”的“特征角”为
,那么这个“特征三角形”的最小内角的度数为
?.
三、解答题(共6小题;共90分)
13.
如图,,
平分
,.求
的度数.
14.
如图,在
中,,,
是
的角平分线,求
的度数.
15.
在
中,,,求
的度数.
16.
如图,在
中,,
分别是
和
的平分线,已知
,求
的度数.
17.
如图,
的内角度数之比为
,
是
的平分线,求
的度数.
18.
如图所示,将
沿
折叠,使点
落在点
处,试探求
,
与
的数量关系.
答案
1.
D
【解析】由题意得
,
故
是钝角三角形.
2.
A
3.
C
4.
B
5.
C
6.
A
7.
C
8.
B
9.
10.
锐角
11.
12.
【解析】根据“特征三角形”和“特征角”的定义可知,如果一个“特征三角形”的“特征角”为
,则另一个内角为
,根据三角形的内角和定理求出第
个角为
,所以这个“特征三角形”的最小内角的度数为
.
13.
,
.
平分
,
,
,
.
14.
是
的角平分线,
.
.
,
.
15.
,
.
,
.
又
,
.
16.
,
.
,
分别是
和
的平分线,
.
.
17.
设
,,
,
.
,
.
是
的平分线,
,
,
.
18.
根据三角形内角和
,知
.
由于折叠,所以
,
.
,
,
.
.
第1页(共5
页)
