专题04 循环规律满分计划-备战2022年中考数学之满分专题专题训练(含解析)
文档属性
| 名称 | 专题04 循环规律满分计划-备战2022年中考数学之满分专题专题训练(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 21:25:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
突破04:“循环规律”满分计划
1.如图,矩形的两边分别在轴、轴上,点与原点重合,点,将矩形沿轴向右翻滚,经过一次翻滚点对应点记为,经过第二次翻滚点对应点记为…以次类推,经过2020次翻滚后点对应点的坐标为( )21·世纪*教育网
A. B.
C. D.
【答案】C
【分析】
观察图形即可得到经过4次翻滚后点A对应点一循环,先求出2020÷4的商和余数,从而解答本题.
【详解】
解:观察图形可得经过4次翻滚后点A对应点一循环,
2020÷4=505,
∵点,矩形的周长为:2(1+2)=6,
∴经过2020次翻滚后点A对应点A2020的坐标为(6×505-1,2),即(3029,2).
故选C.www-2-1-cnjy-com
【点睛】
本题考查探究点的坐标的问题,关键是找到点的变化规律.
2.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点,作正方形;延长交x轴于点,作正方形…按这样的规律进行下去,第2019个正方形的面积为( )2-1-c-n-j-y
A. B.
C. D.
【答案】B
【分析】
根据相似三角形对应边成比例得到正方形的边长,然后观察得到正方形边长的规律,进而表示出正方形的面积.
【详解】
解:∵正方形ABCD的点A的坐标为(1,0),点D的坐标为(0,2)
∴OA=1,OD=2,
∴,,
∵正方形ABCD,正方形
∴∠OAD+∠A1AB=90°,∠ADO+∠OAD=90°,
∴∠A1AB=∠ADO
∵∠AOD=∠A1BA=90°,
∴△A1AB∽△ADO
∴
∵,
∴,
∴第2个正方形的边长:,
同理可得:第3个正方形的边长:
第4个正方形的边长:
……
∴第2019个正方形的边长:,
所以第2019个正方形的面积为:
故答案为:B.
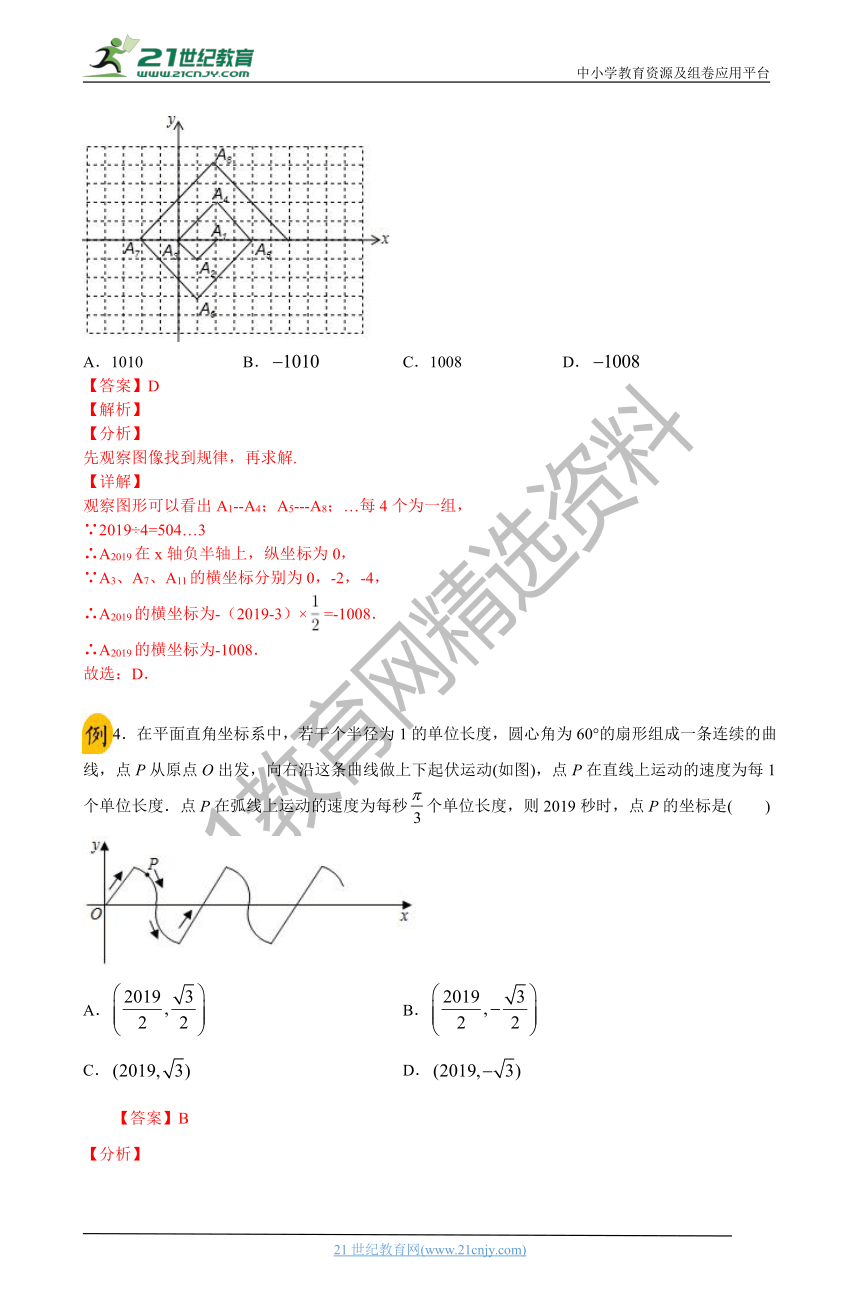
3.如图,在一个单位面积为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,……是斜边在x轴上,且斜边长分别为2,4,6,……的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2?(1,-1),A3(0,0),则依图中所示规律,点A2019的横坐标为( )21cnjy.com
A.1010 B. C.1008 D.
【答案】D
【解析】
【分析】
先观察图像找到规律,再求解.
【详解】
观察图形可以看出A1--A4;A5---A8;…每4个为一组,
∵2019÷4=504…3
∴A2019在x轴负半轴上,纵坐标为0,
∵A3、A7、A11的横坐标分别为0,-2,-4,
∴A2019的横坐标为-(2019-3)×=-1008.
∴A2019的横坐标为-1008.
故选:D.
4.在平面直角坐标系中,若干个半径为1的单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每1个单位长度.点P在弧线上运动的速度为每秒个单位长度,则2019秒时,点P的坐标是( )
A. B.
C. D.
【答案】B
【分析】
设第n秒运动到Pn(n为自然数)点,根据点P的运动规律找出部分Pn点的坐标,根据坐标的变化找出变化规律“P4n+1( ,),P4n+2(n+1,0),P4n+3(,﹣),P4n+4(2n+2,0)”,依此规律即可得出结论.www.21-cn-jy.com
【详解】
解:设第n秒运动到Pn(n为自然数)点,
观察,发现规律:P1(,),P2(1,0),P3(,﹣),P4(2,0),P5(,),…,
∴P4n+1(,),P4n+2(n+1,0),P4n+3(,﹣),P4n+4(2n+2,0).
∵2019=4×504+3,
∴P2019为(,﹣),
故答案为B.
5.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,每个正方形四条边上的整点的个数.按此规律推算出正方形A20B20C20D20四条边上的整点的总个数有( )【来源:21cnj*y.co*m】
A.152 B.156 C.160 D.168
【答案】C
【分析】
分别数出正方形A1B1C_1D1???A2_B2C2D2,A3B3C3D3四条边上的整点的个数.找出规律,按此规律即可推算出正方形A20B20C20D20四条边上的整点的总个数.21*cnjy*com
【详解】
解:观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,
每个正方形四条边上的整点的个数分别为:
8个,即8=1×8,
16个,即16=2×8,
24个,即24=3×8,
…
所以正方形A20B20C20D20四条边上的整点的总个数有:
20×8=160个.
故选:C.
6.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )21世纪教育网版权所有
A.(1,1) B.(0,) C.() D.(﹣1,1)
【答案】D
【解析】
分析:根据图形可知:点B在_???O????????????_以OB为半径的圆上运动,由旋转可知:将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45°,可得对应点B的坐标,根据规律发现是8次一循环,可得结论.21·cn·jy·com
详解:∵四边形OABC是正方形,且OA=1,
∴B(1,1),
连接OB,
由勾股定理得:OB=,
由旋转得:OB=OB1=OB2=OB3=…=,
∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,
相当于将线段OB绕点O逆时针旋转45°,依次得到∠AOB=∠BOB1=∠B1OB2=…=45°,
∴B1(0,),B2(-1,1),B3(-,0),…,
发现是8次一循环,所以2018÷8=252…余2,
∴点B2018的坐标为(-1,1)
故选D.
7.如图,在平面直角坐标系上有个点,点第1次向上跳动1个单位至点,紧接着第2次向右跳动2个单位至点,第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点第2019次跳动至点的坐标是( )21教育网
A. B.
C. D.
【答案】B
【分析】
设第n次跳动至点An,根据部_??????An??????_的变化找出变化规律“A4n(-n-1,2n),A4n+1(-n-1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数)”,依此规律结合2019=504×4+3即可得出点A2019的坐标.2·1·c·n·j·y
【详解】
解:设第n次跳动至点An,
观察,发现:A(-1,0)_???A1???-1_,1),A2(1,1),A3(1,2),A4(-2,2),A5(-2,3),A6(2,3),A7(2,4),A8(-3,4),A9(-3,5),…,【来源:21·世纪·教育·网】
∴A4n(-n-1,2n),A4_n+1???-n_-1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数).
∵2019=504×4+3
∴A2019(504+1,504×2+2),即.
故选:B.
_21?????????è?????(www.21cnjy.com)_
突破04:“循环规律”满分计划
1.如图,矩形的两边分别在轴、轴上,点与原点重合,点,将矩形沿轴向右翻滚,经过一次翻滚点对应点记为,经过第二次翻滚点对应点记为…以次类推,经过2020次翻滚后点对应点的坐标为( )21·世纪*教育网
A. B.
C. D.
【答案】C
【分析】
观察图形即可得到经过4次翻滚后点A对应点一循环,先求出2020÷4的商和余数,从而解答本题.
【详解】
解:观察图形可得经过4次翻滚后点A对应点一循环,
2020÷4=505,
∵点,矩形的周长为:2(1+2)=6,
∴经过2020次翻滚后点A对应点A2020的坐标为(6×505-1,2),即(3029,2).
故选C.www-2-1-cnjy-com
【点睛】
本题考查探究点的坐标的问题,关键是找到点的变化规律.
2.在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点,作正方形;延长交x轴于点,作正方形…按这样的规律进行下去,第2019个正方形的面积为( )2-1-c-n-j-y
A. B.
C. D.
【答案】B
【分析】
根据相似三角形对应边成比例得到正方形的边长,然后观察得到正方形边长的规律,进而表示出正方形的面积.
【详解】
解:∵正方形ABCD的点A的坐标为(1,0),点D的坐标为(0,2)
∴OA=1,OD=2,
∴,,
∵正方形ABCD,正方形
∴∠OAD+∠A1AB=90°,∠ADO+∠OAD=90°,
∴∠A1AB=∠ADO
∵∠AOD=∠A1BA=90°,
∴△A1AB∽△ADO
∴
∵,
∴,
∴第2个正方形的边长:,
同理可得:第3个正方形的边长:
第4个正方形的边长:
……
∴第2019个正方形的边长:,
所以第2019个正方形的面积为:
故答案为:B.
3.如图,在一个单位面积为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,……是斜边在x轴上,且斜边长分别为2,4,6,……的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2?(1,-1),A3(0,0),则依图中所示规律,点A2019的横坐标为( )21cnjy.com
A.1010 B. C.1008 D.
【答案】D
【解析】
【分析】
先观察图像找到规律,再求解.
【详解】
观察图形可以看出A1--A4;A5---A8;…每4个为一组,
∵2019÷4=504…3
∴A2019在x轴负半轴上,纵坐标为0,
∵A3、A7、A11的横坐标分别为0,-2,-4,
∴A2019的横坐标为-(2019-3)×=-1008.
∴A2019的横坐标为-1008.
故选:D.
4.在平面直角坐标系中,若干个半径为1的单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每1个单位长度.点P在弧线上运动的速度为每秒个单位长度,则2019秒时,点P的坐标是( )
A. B.
C. D.
【答案】B
【分析】
设第n秒运动到Pn(n为自然数)点,根据点P的运动规律找出部分Pn点的坐标,根据坐标的变化找出变化规律“P4n+1( ,),P4n+2(n+1,0),P4n+3(,﹣),P4n+4(2n+2,0)”,依此规律即可得出结论.www.21-cn-jy.com
【详解】
解:设第n秒运动到Pn(n为自然数)点,
观察,发现规律:P1(,),P2(1,0),P3(,﹣),P4(2,0),P5(,),…,
∴P4n+1(,),P4n+2(n+1,0),P4n+3(,﹣),P4n+4(2n+2,0).
∵2019=4×504+3,
∴P2019为(,﹣),
故答案为B.
5.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点,请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,每个正方形四条边上的整点的个数.按此规律推算出正方形A20B20C20D20四条边上的整点的总个数有( )【来源:21cnj*y.co*m】
A.152 B.156 C.160 D.168
【答案】C
【分析】
分别数出正方形A1B1C_1D1???A2_B2C2D2,A3B3C3D3四条边上的整点的个数.找出规律,按此规律即可推算出正方形A20B20C20D20四条边上的整点的总个数.21*cnjy*com
【详解】
解:观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,
每个正方形四条边上的整点的个数分别为:
8个,即8=1×8,
16个,即16=2×8,
24个,即24=3×8,
…
所以正方形A20B20C20D20四条边上的整点的总个数有:
20×8=160个.
故选:C.
6.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )21世纪教育网版权所有
A.(1,1) B.(0,) C.() D.(﹣1,1)
【答案】D
【解析】
分析:根据图形可知:点B在_???O????????????_以OB为半径的圆上运动,由旋转可知:将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,相当于将线段OB绕点O逆时针旋转45°,可得对应点B的坐标,根据规律发现是8次一循环,可得结论.21·cn·jy·com
详解:∵四边形OABC是正方形,且OA=1,
∴B(1,1),
连接OB,
由勾股定理得:OB=,
由旋转得:OB=OB1=OB2=OB3=…=,
∵将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,
相当于将线段OB绕点O逆时针旋转45°,依次得到∠AOB=∠BOB1=∠B1OB2=…=45°,
∴B1(0,),B2(-1,1),B3(-,0),…,
发现是8次一循环,所以2018÷8=252…余2,
∴点B2018的坐标为(-1,1)
故选D.
7.如图,在平面直角坐标系上有个点,点第1次向上跳动1个单位至点,紧接着第2次向右跳动2个单位至点,第3次向上跳动1个单位,第4次向左跳动3个单位,第5次又向上跳动1个单位,第6次向右跳动4个单位,…,依次规律跳动下去,点第2019次跳动至点的坐标是( )21教育网
A. B.
C. D.
【答案】B
【分析】
设第n次跳动至点An,根据部_??????An??????_的变化找出变化规律“A4n(-n-1,2n),A4n+1(-n-1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数)”,依此规律结合2019=504×4+3即可得出点A2019的坐标.2·1·c·n·j·y
【详解】
解:设第n次跳动至点An,
观察,发现:A(-1,0)_???A1???-1_,1),A2(1,1),A3(1,2),A4(-2,2),A5(-2,3),A6(2,3),A7(2,4),A8(-3,4),A9(-3,5),…,【来源:21·世纪·教育·网】
∴A4n(-n-1,2n),A4_n+1???-n_-1,2n+1),A4n+2(n+1,2n+1),A4n+3(n+1,2n+2)(n为自然数).
∵2019=504×4+3
∴A2019(504+1,504×2+2),即.
故选:B.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
