专题05 拓展探究步步为营-备战2022年中考数学之满分专题专题训练(含解析)
文档属性
| 名称 | 专题05 拓展探究步步为营-备战2022年中考数学之满分专题专题训练(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 21:27:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
突破05:“拓展探究”步步为营
1.将正方形的边绕点逆时针旋转至 ,记旋转角为.连接,过点作垂直于直线,垂足为点,连接,21教育网
如图1,当时,的形状为 ,连接,可求出的值为 ;
当且时,
①中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
②当以点为顶点的四边形是平行四边形时,请直接写出的值.
【答案】(1)等腰直角三角形,;(2)①结论不变,理由见解析;②3或1.
【分析】
(1)根据题意,证明是等边三角形,得,计算出,根据,可得为等腰直角三角形;证明,可得的值;
(2)①连接BD,通过正方形性质及旋转,表示出,结合,可得为等腰直角三角形;证明,可得的值;
②分为以CD为边和CD为对角线两种情况进行讨论即可.
【详解】
(1)由题知°,°,
∴°,且为等边三角形
∴°,
∴
∵
∴°
∴°
∴为等腰直角三角形
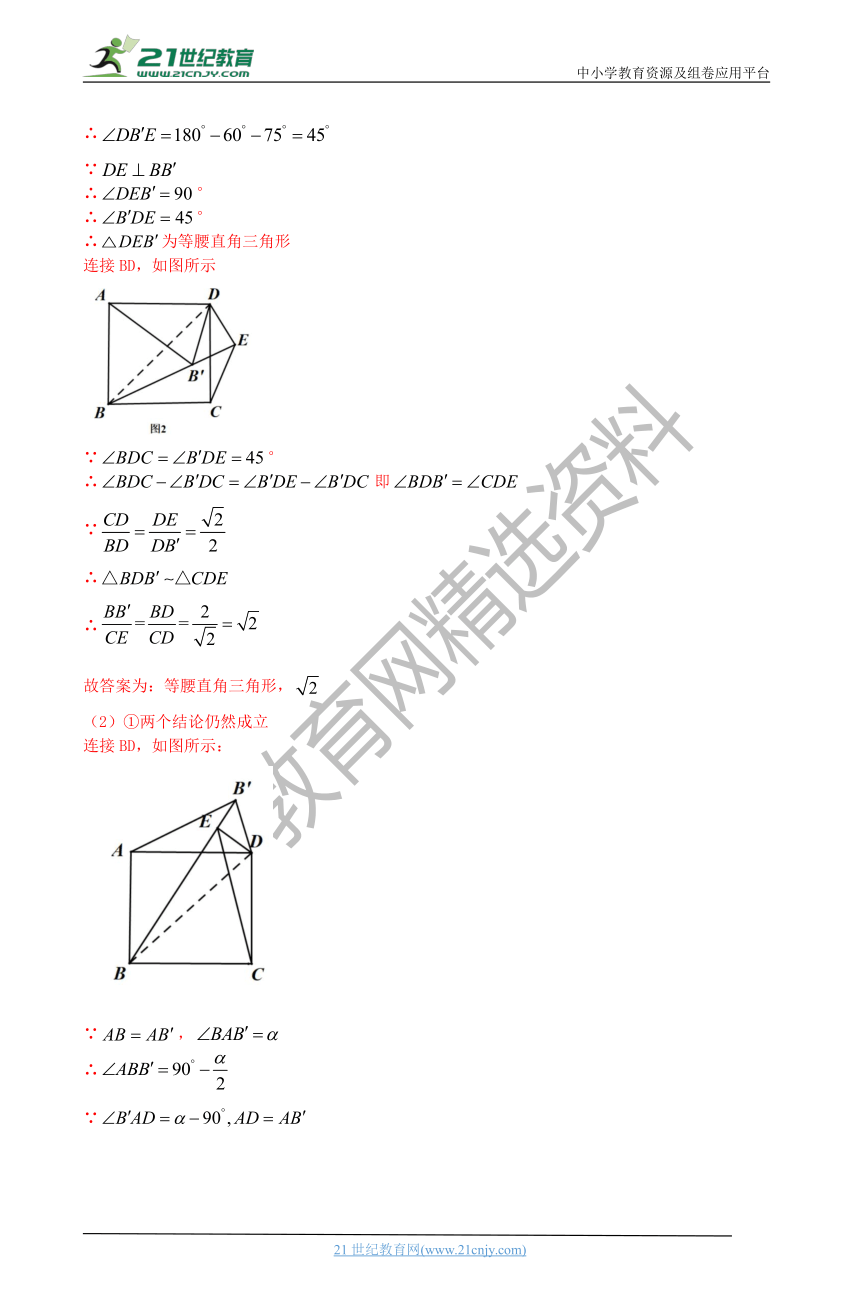
连接BD,如图所示
∵°
∴即
∵
∴
∴
故答案为:等腰直角三角形,
(2)①两个结论仍然成立
连接BD,如图所示:
∵,
∴
∵
∴
∴
∵
∴
∴是等腰直角三角形
∴
∵四边形为正方形
∴
∴
∵
∴
∴
∴
∴结论不变,依然成立
②若以点为顶点的四边形是平行四边形时,分两种情况讨论
第一种:以CD为边时,则,此时点在线段BA的延长线上,
如图所示:
此时点E与点A重合,
∴,得;
②当以CD为对角线时,如图所示:
此时点F为CD中点,
∵
∴
∵
∴
∴
∴
∴
∴
综上:的值为3或1.
2.在,,.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.21·cn·jy·com
(1)观察猜想
如图1,当时,的值是 ,直线BD与直线CP相交所成的较小角的度数是 .
(2)类比探究
如图2,当时,请写出的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
(3)解决问题
当时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时的值.www.21-cn-jy.com
【答案】(1)1,(2)45°(3),
【分析】
(1)如图1中,延长CP交BD的延长线于E,设AB交EC于点O.证明,即可解决问题.
(2)如图2中,设BD交AC于点O,BD交PC于点E.证明,即可解决问题.
(3)分两种情形:①如图3﹣1中,当点D在线段PC上时,延长AD交BC的延长线于H.证明即可解决问题.2·1·c·n·j·y
②如图3﹣2中,当点P在线段CD上时,同法可证:解决问题.
【详解】
解:(1)如图1中,延长CP交BD的延长线于E,设AB交EC于点O.
,
,
,,
,
,,
,
,
,线BD与直线CP相交所成的较小角的度数是,
故答案为1,.
(2)如图2中,设BD交AC于点O,BD交PC于点E.
,
,
,
,
,,
,
,
直线BD与直线CP相交所成的小角的度数为.
(3)如图3﹣1中,当点D在线段PC上时,延长AD交BC的延长线于H.
,,
,
,
,
,
,
,
,,
,
,
,
,
,
,
,
,
,
A,D,C,B四点共圆,
,,
,
,设,则,,
c.
如图3﹣2中,当点P在线段CD上时,同法可证:,设,则,,
,
.
3.如图①,在中,,,点、分别在边、上,,连接,点、、分别为、、的中点.21世纪教育网版权所有
(1)观察猜想:图①中,线段与的数量关系是_____________,用含的代数式表示的度数是________________________;【来源:21·世纪·教育·网】
(2)探究证明:把绕点顺时针方向旋转到图②的位置,连接,,,当时,判断的形状,并说明理由;21·世纪*教育网
(3)拓展延伸:把绕点在平面内任意旋转,若,,,请直接写出线段的最大值和最小值.
【答案】(1)MP= NP,180°-;(2)是等边三角形,证明见解析;(3)的最大值为,最小值为21*cnjy*com
【分析】
(1)由三角形的中位线的判定与性质不难得出,MP=BD,MPBD以及NP=CE,NPCE,因此MP= NP,将利用平行线的性质转化为与的和求解即可.
(2)有(1)同理可证MP= NP,MPBD,NPCE,在根据平行线的性质以及三角形外角的性质将转化为,,,这四个角的和,求出的度数,判断的形状即可.21cnjy.com
(3)由题意不难得出M的运动轨迹是以点A为圆心,为半径的一个圆,分别找出MN最大与最小时M的位置,分别求出最大最小值即可.【来源:21cnj*y.co*m】
【详解】
(1)AB=AC,AD=DE,
BD=EC,
M、P分别是DE、BE的中点,
MP=BD,MPBD,
,
同理可证:NP=CE,NPCE,
MP= NP,
,
=+=+=180°-.
(2)由旋转可得:,AD=AE,
,
在与中,
,
≌,
CE=BD,
由(1)同理可证MP=BD,MPBD,NP=CE,NPCE,
MP= NP,
是等腰三角形,
==+,
=+=+,
=+=+++=180°-120°=60°,
是等边三角形.
(3)等腰直角中,AD=3,
DE=3,
M是DE的中点,
AM=,
M的运动轨迹是以点A为圆心,为半径的一个圆,
如图,连接NA并延长分别交⊙A于点M1、M2,
等腰直角中,AB=7,
BC=7,
N是BC的中点,
AN=,ANBC,
当点M旋转至M1位置时,最大,=+=;
当点M旋转至M2位置时,最小,=-=.
4.如图,为等边三角形,点为线段的中点,连接,点在线段上,将线段绕点顺时针旋转到,连接,连接交于点.
(1)如图1,当点与点重合时,直接写出线段和线段的数量关系;
(2)如图2,当时,过点作的平行线交于点,请写出线段与的数量关系,并说明理由;
(3)在(2)的条件下,当时,请直接写出点到直线的距离.
【答案】(1);(2),证明见解析;(3)
【详解】
解:(1)
∵为等边三角形
∴
∴
∴
∴
(2)
证明:
为等边三角形
∴
∵,
∴,
∴为等边三角形
∴,
∴
∴,
∵,为的中点,
∴,∴
∵为等边三角形
∴
∴
∴
∴
∴
∴
在中
∴
∴
∴
(3)过O作NEBC于E
∵,点为线段的中点,
∴
在Rt中,,
∴
∴MN=3,
∵,
∴
∴,
∴
∴
∴
∵△MNC的面积=点到直线的距离
∴点到直线的距离
∴点到直线的距离=
5.探究:如图1和图2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.www-2-1-cnjy-com
(1)①如图1,若∠B_??????ADCé??_是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,直接写出线段BE、DF和EF之间的数量关系 ;2-1-c-n-j-y
②如图2,若∠B、∠D_é???????????è§????_但满足∠B+∠D=180°,线段BE、DF和EF之间的结论是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由.【出处:21教育名师】
(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2.点D、E均在边BC边上,且∠DAE=45°,若BD=1,求DE的长.【版权所有:21教育】
【答案】(1)①EF=BE+DF;②成立,理由详见解析;(2)DE=.
【分析】
(1)①根据旋转_?????§è?¨??????A_E=AG,∠BAE=∠DAG,BE=DG,求出∠EAF=∠GAF=45°,根据SAS推出△EAF≌△GAF,根据全等三角形的性质得出EF=GF,即可求出答案;21教育名师原创作品
②根据旋转的性质作辅_???????????????A_E=AG,∠B=∠ADG,∠BAE=∠DAG,求出C、D、G在一条直线上,根据SAS推出△EAF≌△GAF,根据全等三角形的性质得出EF=GF,即可求出答案;
(2)如图3,同理作旋转_???è§?????????????_等腰直角三角形性质和勾股定理求出∠ABC=∠C=45°,BC=4,根据旋转的性质得出AF=AE,∠FBA=∠C=45°,∠BAF=∠CAE,求出∠FAD=∠DAE=45°,证△FAD≌△EAD,根据全等得出DF=DE,设DE=x,则DF=x,BF=CE=3﹣x,根据勾股定理得出方程,求出x即可.21*cnjy*com
【详解】
解:(1)∵把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,
∴AE=AG,∠BAE=∠DAG,BE=DG,∠B=∠ADG=90°,
∵∠ADC=90°,
∴∠ADC+∠ADG=90°
∴F、D、G共线,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠DAG+∠DAF=45°,
即∠EAF=∠GAF=45°,
在△EAF和△GAF中,
∵,
∴△EAF≌△GAF(SAS),
∴EF=GF,
∵BE=DG,
∴EF=GF=DF+DG=BE+DF,
故答案为:EF=BE+DF;
②成立,
理由:如图2,把△ABE绕A点旋转到△ADG,使AB和AD重合,
则AE=AG,∠B=∠ADG,∠BAE=∠DAG,
∵∠B+∠ADC=180°,
∴∠ADC+∠ADG=180°,
∴C、D、G在一条直线上,
与①同理得,∠EAF=∠GAF=45°,
在△EAF和△GAF中,
∵,
∴△EAF≌△GAF(SAS),
∴EF=GF,
∵BE=DG,
∴EF=GF=BE+DF;
(2)解:∵△ABC中,AB=AC=2,∠BAC=90°,
∴∠ABC=∠C=45°,
由勾股定理得:BC==4,
如图3,把△AEC绕A点旋转到△AFB,使AB和AC重合,连接DF,
则AF=AE,∠FBA=∠C=45°,∠BAF=∠CAE,
∵∠DAE=45°,
∴∠FAD=∠FAB+∠BAD=∠CAE+∠BAD=∠BAC﹣∠DAE=90°﹣45°=45°,
∴∠FAD=∠DAE=45°,
在△FAD和△EAD中,
∴△FAD≌△EAD(SAS),
∴DF=DE,
设DE=x,则DF=x,
∵BC=4,
∴BF=CE=4﹣1﹣x=3﹣x,
∵∠FBA=45°,∠ABC=45°,
∴∠FBD=90°,
由勾股定理得:DF2=BF2+BD2,
x2=(3﹣x)2+12,
解得:x=,
即DE=.
_21?????????è?????(www.21cnjy.com)_
突破05:“拓展探究”步步为营
1.将正方形的边绕点逆时针旋转至 ,记旋转角为.连接,过点作垂直于直线,垂足为点,连接,21教育网
如图1,当时,的形状为 ,连接,可求出的值为 ;
当且时,
①中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;
②当以点为顶点的四边形是平行四边形时,请直接写出的值.
【答案】(1)等腰直角三角形,;(2)①结论不变,理由见解析;②3或1.
【分析】
(1)根据题意,证明是等边三角形,得,计算出,根据,可得为等腰直角三角形;证明,可得的值;
(2)①连接BD,通过正方形性质及旋转,表示出,结合,可得为等腰直角三角形;证明,可得的值;
②分为以CD为边和CD为对角线两种情况进行讨论即可.
【详解】
(1)由题知°,°,
∴°,且为等边三角形
∴°,
∴
∵
∴°
∴°
∴为等腰直角三角形
连接BD,如图所示
∵°
∴即
∵
∴
∴
故答案为:等腰直角三角形,
(2)①两个结论仍然成立
连接BD,如图所示:
∵,
∴
∵
∴
∴
∵
∴
∴是等腰直角三角形
∴
∵四边形为正方形
∴
∴
∵
∴
∴
∴
∴结论不变,依然成立
②若以点为顶点的四边形是平行四边形时,分两种情况讨论
第一种:以CD为边时,则,此时点在线段BA的延长线上,
如图所示:
此时点E与点A重合,
∴,得;
②当以CD为对角线时,如图所示:
此时点F为CD中点,
∵
∴
∵
∴
∴
∴
∴
∴
综上:的值为3或1.
2.在,,.点P是平面内不与点A,C重合的任意一点.连接AP,将线段AP绕点P逆时针旋转α得到线段DP,连接AD,BD,CP.21·cn·jy·com
(1)观察猜想
如图1,当时,的值是 ,直线BD与直线CP相交所成的较小角的度数是 .
(2)类比探究
如图2,当时,请写出的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.
(3)解决问题
当时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时的值.www.21-cn-jy.com
【答案】(1)1,(2)45°(3),
【分析】
(1)如图1中,延长CP交BD的延长线于E,设AB交EC于点O.证明,即可解决问题.
(2)如图2中,设BD交AC于点O,BD交PC于点E.证明,即可解决问题.
(3)分两种情形:①如图3﹣1中,当点D在线段PC上时,延长AD交BC的延长线于H.证明即可解决问题.2·1·c·n·j·y
②如图3﹣2中,当点P在线段CD上时,同法可证:解决问题.
【详解】
解:(1)如图1中,延长CP交BD的延长线于E,设AB交EC于点O.
,
,
,,
,
,,
,
,
,线BD与直线CP相交所成的较小角的度数是,
故答案为1,.
(2)如图2中,设BD交AC于点O,BD交PC于点E.
,
,
,
,
,,
,
,
直线BD与直线CP相交所成的小角的度数为.
(3)如图3﹣1中,当点D在线段PC上时,延长AD交BC的延长线于H.
,,
,
,
,
,
,
,
,,
,
,
,
,
,
,
,
,
,
A,D,C,B四点共圆,
,,
,
,设,则,,
c.
如图3﹣2中,当点P在线段CD上时,同法可证:,设,则,,
,
.
3.如图①,在中,,,点、分别在边、上,,连接,点、、分别为、、的中点.21世纪教育网版权所有
(1)观察猜想:图①中,线段与的数量关系是_____________,用含的代数式表示的度数是________________________;【来源:21·世纪·教育·网】
(2)探究证明:把绕点顺时针方向旋转到图②的位置,连接,,,当时,判断的形状,并说明理由;21·世纪*教育网
(3)拓展延伸:把绕点在平面内任意旋转,若,,,请直接写出线段的最大值和最小值.
【答案】(1)MP= NP,180°-;(2)是等边三角形,证明见解析;(3)的最大值为,最小值为21*cnjy*com
【分析】
(1)由三角形的中位线的判定与性质不难得出,MP=BD,MPBD以及NP=CE,NPCE,因此MP= NP,将利用平行线的性质转化为与的和求解即可.
(2)有(1)同理可证MP= NP,MPBD,NPCE,在根据平行线的性质以及三角形外角的性质将转化为,,,这四个角的和,求出的度数,判断的形状即可.21cnjy.com
(3)由题意不难得出M的运动轨迹是以点A为圆心,为半径的一个圆,分别找出MN最大与最小时M的位置,分别求出最大最小值即可.【来源:21cnj*y.co*m】
【详解】
(1)AB=AC,AD=DE,
BD=EC,
M、P分别是DE、BE的中点,
MP=BD,MPBD,
,
同理可证:NP=CE,NPCE,
MP= NP,
,
=+=+=180°-.
(2)由旋转可得:,AD=AE,
,
在与中,
,
≌,
CE=BD,
由(1)同理可证MP=BD,MPBD,NP=CE,NPCE,
MP= NP,
是等腰三角形,
==+,
=+=+,
=+=+++=180°-120°=60°,
是等边三角形.
(3)等腰直角中,AD=3,
DE=3,
M是DE的中点,
AM=,
M的运动轨迹是以点A为圆心,为半径的一个圆,
如图,连接NA并延长分别交⊙A于点M1、M2,
等腰直角中,AB=7,
BC=7,
N是BC的中点,
AN=,ANBC,
当点M旋转至M1位置时,最大,=+=;
当点M旋转至M2位置时,最小,=-=.
4.如图,为等边三角形,点为线段的中点,连接,点在线段上,将线段绕点顺时针旋转到,连接,连接交于点.
(1)如图1,当点与点重合时,直接写出线段和线段的数量关系;
(2)如图2,当时,过点作的平行线交于点,请写出线段与的数量关系,并说明理由;
(3)在(2)的条件下,当时,请直接写出点到直线的距离.
【答案】(1);(2),证明见解析;(3)
【详解】
解:(1)
∵为等边三角形
∴
∴
∴
∴
(2)
证明:
为等边三角形
∴
∵,
∴,
∴为等边三角形
∴,
∴
∴,
∵,为的中点,
∴,∴
∵为等边三角形
∴
∴
∴
∴
∴
∴
在中
∴
∴
∴
(3)过O作NEBC于E
∵,点为线段的中点,
∴
在Rt中,,
∴
∴MN=3,
∵,
∴
∴,
∴
∴
∴
∵△MNC的面积=点到直线的距离
∴点到直线的距离
∴点到直线的距离=
5.探究:如图1和图2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.www-2-1-cnjy-com
(1)①如图1,若∠B_??????ADCé??_是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,直接写出线段BE、DF和EF之间的数量关系 ;2-1-c-n-j-y
②如图2,若∠B、∠D_é???????????è§????_但满足∠B+∠D=180°,线段BE、DF和EF之间的结论是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由.【出处:21教育名师】
(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2.点D、E均在边BC边上,且∠DAE=45°,若BD=1,求DE的长.【版权所有:21教育】
【答案】(1)①EF=BE+DF;②成立,理由详见解析;(2)DE=.
【分析】
(1)①根据旋转_?????§è?¨??????A_E=AG,∠BAE=∠DAG,BE=DG,求出∠EAF=∠GAF=45°,根据SAS推出△EAF≌△GAF,根据全等三角形的性质得出EF=GF,即可求出答案;21教育名师原创作品
②根据旋转的性质作辅_???????????????A_E=AG,∠B=∠ADG,∠BAE=∠DAG,求出C、D、G在一条直线上,根据SAS推出△EAF≌△GAF,根据全等三角形的性质得出EF=GF,即可求出答案;
(2)如图3,同理作旋转_???è§?????????????_等腰直角三角形性质和勾股定理求出∠ABC=∠C=45°,BC=4,根据旋转的性质得出AF=AE,∠FBA=∠C=45°,∠BAF=∠CAE,求出∠FAD=∠DAE=45°,证△FAD≌△EAD,根据全等得出DF=DE,设DE=x,则DF=x,BF=CE=3﹣x,根据勾股定理得出方程,求出x即可.21*cnjy*com
【详解】
解:(1)∵把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,
∴AE=AG,∠BAE=∠DAG,BE=DG,∠B=∠ADG=90°,
∵∠ADC=90°,
∴∠ADC+∠ADG=90°
∴F、D、G共线,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠DAG+∠DAF=45°,
即∠EAF=∠GAF=45°,
在△EAF和△GAF中,
∵,
∴△EAF≌△GAF(SAS),
∴EF=GF,
∵BE=DG,
∴EF=GF=DF+DG=BE+DF,
故答案为:EF=BE+DF;
②成立,
理由:如图2,把△ABE绕A点旋转到△ADG,使AB和AD重合,
则AE=AG,∠B=∠ADG,∠BAE=∠DAG,
∵∠B+∠ADC=180°,
∴∠ADC+∠ADG=180°,
∴C、D、G在一条直线上,
与①同理得,∠EAF=∠GAF=45°,
在△EAF和△GAF中,
∵,
∴△EAF≌△GAF(SAS),
∴EF=GF,
∵BE=DG,
∴EF=GF=BE+DF;
(2)解:∵△ABC中,AB=AC=2,∠BAC=90°,
∴∠ABC=∠C=45°,
由勾股定理得:BC==4,
如图3,把△AEC绕A点旋转到△AFB,使AB和AC重合,连接DF,
则AF=AE,∠FBA=∠C=45°,∠BAF=∠CAE,
∵∠DAE=45°,
∴∠FAD=∠FAB+∠BAD=∠CAE+∠BAD=∠BAC﹣∠DAE=90°﹣45°=45°,
∴∠FAD=∠DAE=45°,
在△FAD和△EAD中,
∴△FAD≌△EAD(SAS),
∴DF=DE,
设DE=x,则DF=x,
∵BC=4,
∴BF=CE=4﹣1﹣x=3﹣x,
∵∠FBA=45°,∠ABC=45°,
∴∠FBD=90°,
由勾股定理得:DF2=BF2+BD2,
x2=(3﹣x)2+12,
解得:x=,
即DE=.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
