专题08 个性函数图像满分计划-备战2022年中考数学之满分专题专题训练(含解析)
文档属性
| 名称 | 专题08 个性函数图像满分计划-备战2022年中考数学之满分专题专题训练(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 21:34:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
突破08:“个性函数图像”满分计划
1.小亮在学习中遇到这样一个问题:
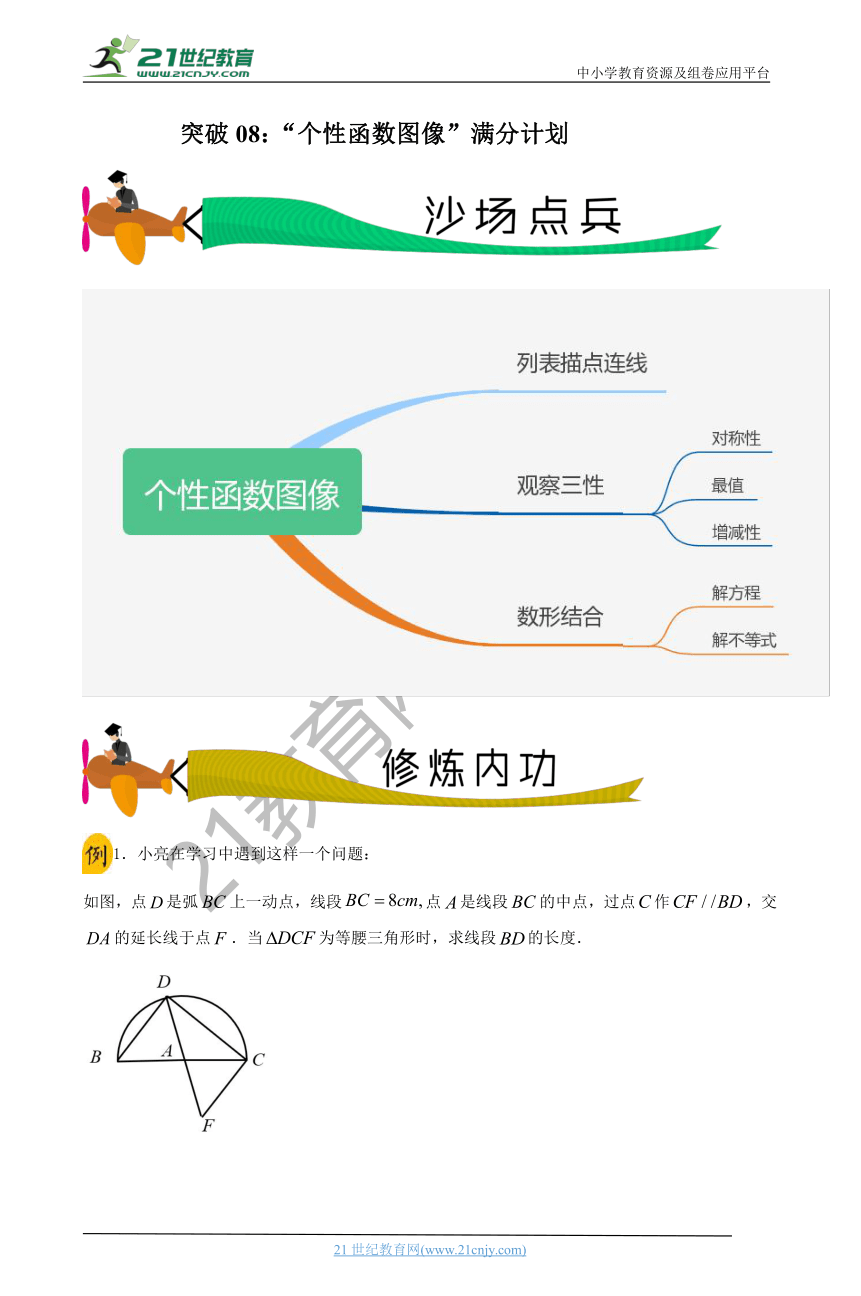
如图,点是弧上一动点,线段点是线段的中点,过点作,交的延长线于点.当为等腰三角形时,求线段的长度.2·1·c·n·j·y
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题,请将下面的探究过程补充完整:【来源:21·世纪·教育·网】
根据点在弧上的不同位置,画出相应的图形,测量线段的长度,得到下表的几组对应值.
操作中发现:
①"当点为弧的中点时, ".则上中的值是
②"线段的长度无需测量即可得到".请简要说明理由;
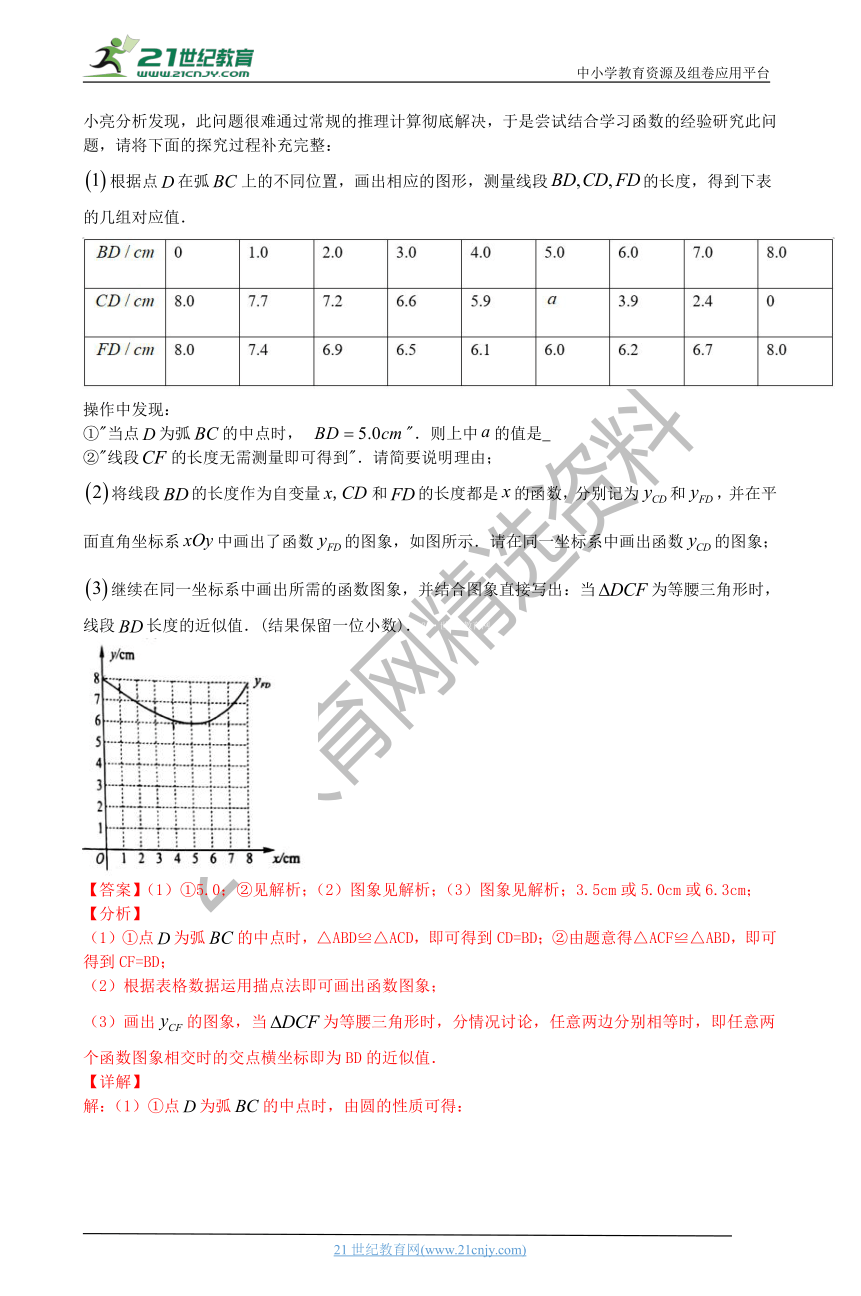
将线段的长度作为自变量和的长度都是的函数,分别记为和,并在平面直角坐标系中画出了函数的图象,如图所示.请在同一坐标系中画出函数的图象;
继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当为等腰三角形时,线段长度的近似值.(结果保留一位小数).21·世纪*教育网
【答案】(1)①5.0;②见解析;(2)图象见解析;(3)图象见解析;3.5cm或5.0cm或6.3cm;
【分析】
(1)①点为弧的中点时,△ABD≌△ACD,即可得到CD=BD;②由题意得△ACF≌△ABD,即可得到CF=BD;21*cnjy*com
(2)根据表格数据运用描点法即可画出函数图象;
(3)画出的图象,当为等腰三角形时,分情况讨论,任意两边分别相等时,即任意两个函数图象相交时的交点横坐标即为BD的近似值.【来源:21cnj*y.co*m】
【详解】
解:(1)①点为弧的中点时,由圆的性质可得:
,
∴△ABD≌△ACD,
∴CD=BD=5.0,
∴;
②∵,
∴,
∵,
∴△ACF≌△ABD,
∴CF=BD,
∴线段的长度无需测量即可得到;
(2)函数的图象如图所示:
(3)由(1)知,
画出的图象,如上图所示,当为等腰三角形时,
①,BD为与函数图象的交点横坐标,即BD=5.0cm;
②,BD为与函数图象的交点横坐标,即BD=6.3cm;
③,BD为与函数图象的交点横坐标,即BD=3.5cm;
综上:当为等腰三角形时,线段长度的近似值为3.5cm或5.0cm或6.3cm.
2.有这样一个问题:探究函数的图象与性质.下面是小文的探究过程,请补充完整:
(1)函数的自变量的取值范围是__________;
(2)下表是与的几组对应值:
如图,在平面直角坐标系中,描出了以上表中各对应值为坐标的点.
①观察图中各点的位置发现:点和,和,和,和均关于某点中心对称,则该点的坐标为__________;【出处:21教育名师】
②小文分析函数表达式发现:当时,该函数的最大值为0,则该函数图象在直线左侧的最高点的坐标为__________;【版权所有:21教育】
(3)小文补充了该函数图象上两个点,.
①在上图中描出这两个点,并画出该函数的图象;
②写出该函数的一条性质:__________.
【答案】(1)x≠1;(2)①(1,1);②(0,0);(3)①作图见解析;②当x<0时,y随x的增大而增大(答案不唯一).21教育名师原创作品
【解析】
【分析】
(1)分式的分母不等于零;
(2)①根据中心对称的性质和所对应的点点坐标即可求得,
②根据函数的性质求得即可;
(3)①根据坐标系中的点,用平滑的直线连接即可;
②可以从增减性、渐近性、连续性、与坐标轴交点、图象所在象限等方面作答.
【详解】
解:(1)依题意得:2x-2≠0,
解得x≠1,
故答案是:x≠1;
(2)①点A1和B1,A2和B2,A3和B3,A4和B4均关于某点中心对称,B1(0,0),A1(2,2),
∴中心点点坐标为(1,1);
②∵当x<1时,该函数的最大值为0,
∴该函数图象在直线x=1左侧的最高点的坐标为(0,0);
故答案为(1,1);(0,0);
(3)①
②该函数的性质:
(ⅰ)当x<0时,y随x的增大而增大;
当0≤x<1时,y随x的增大而减小;
当1<x<2时,y随x的增大而减小;
当x≥2时,y随x的增大而增大.
(ⅱ)函数的图象经过第一、三、四象限.
(ⅲ)函数的图象与直线x=1无交点,图象由两部分组成.
故答案为当x<0时,y随x的增大而增大(答案不唯一);
3.如图1,在四边形中,对角线平分.为了研究图中线段之间的数量关系,设.
(1)由题意可得,(在括号内填入图1中相应的线段)y关于x的函数表达式为________;
(2)如图2,在平面直角坐标系中,根据(1)中y关于x的函数表达式描出了其图象上的一部分点,请依据描出的点画出该函数的图象;21世纪教育网版权所有
(3)结合函数图象,解决问题:
①写出该函数的一条性质:__________________________;
②估计的最小值为__________.(结果精确到0.1)
【答案】(1),.(2)图见解析(3)①当时,y随x的增大而增大(答案不唯一). ②4.8.
【分析】
(1)通过证明△ABC∽△ACD,得到,再把相关数据代入求解即可;
(2)用平滑的曲线将平面直角坐标系上的点连接起来即可;
(3)观察图象,写出其性质即可;
(4)观察图象,找出y的最小值对应的x,即可求出AB+AD的最小值.
【详解】
(1)∵平分,
∴
又∵,
∴△ABC∽△ACD
∴,
∵
∴
∴
∴
故答案为:,.
(2)如图所示:
(3)①当时,y随x的增大而增大(答案不唯一).
故答案为:当时,y随x的增大而增大(答案不唯一).
②AB+AD=x+
观察图象可得,y有最小值时,x约为0.7,
故AB+AD的最小值约为:x+=0.7+
故答案为:4.8.
4.有这样一个问题,探究函数y=x2﹣2的图象与性质,小张根据学习函数的经验,对函数y=x2﹣2的图象与性质进行了研究,下面是小张的探究过程,请补充完整:
(1)函数y=x2﹣2的自变量取值范围是 .
(2)下表是y与x的几组对应值:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 4
y … n 3 0 ﹣1 0 ﹣1 0 3 m
求m的值;
(3)如图,在平面直角坐标系xOy中,算出了以上表中各对对应值为坐标的点,根据算出的点,画出该函数的图象;www.21-cn-jy.com
(4)进一步探究发现,该函数图象在第四象限内的最低点是(1,﹣1),结合函数的图象,写出该函数的其他性质(一条即可);www-2-1-cnjy-com
(5)根据图象回答:方程x2﹣2=﹣有 个实数解.
【答案】(1)自变量取值范围是任意实数;(2)m的值为8;(3)如图见解析;(4)当x<﹣1时,y随x的增大而减小.(5)方程x2﹣2=﹣有3个实数解.2-1-c-n-j-y
【分析】
(1)根据二次根式的意义和函数关系式即可求解;
(2)根据函数关系式将x的值代入即可求解;
(3)根据表格数据,描点,连线,即可画出图象;
(4)观察函数图像,利用增减性写出一条性质;
(5)根据图象将y=x2-2的图象向下平移0.5个单位长度与原函数图象有三个交点即可求解.
【详解】
(1)根据函数解析式可知:无论x为何值,均有意义,
∴自变量取值范围是任意实数.
故答案为任意实数.
(2)当x=4时,y=.
答:m的值为8.
(3)如图:
(4)根据函数图象可知:
当x<﹣1时,y随x的增大而减小.
(5)根据图象可知:
直线y=﹣,与函数图象有三个交点,即可得:
方程x2﹣2=﹣有3个实数解.
5.有这样一个问题:探究函数的图象与性质.
小菲根据学习函数的经验,对函数的图象与性质进行了探究.
下面是小菲的探究过程,请补充完整:
(1)函数的自变量的取值范围是___________________.
(2)下表是与的几组对应值.
…
1 2 3 …
…
2
…
表中的值为____________________________.
(3)如下图,在平面直角坐标系中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
(4)根据画出的函数图象,写出:
①时,对应的函数值约为__________________(结果保留一位小数);
②该函数的一条性质:________________________________________________________.
【答案】(1);(2);(3)图像见详解;(4)①1.9;②该函数的一条性质:该函数没有最大值也没有最小值(答案不唯一);21cnjy.com
解:(1)函数的自变量的取值范围是;
(2)根据图表可知当时的函数值为m,把代入,
得:,
∴;
(3)函数图像如下图示:
;
(4)①由(3)中的函数图像可知,当时,对应的函数值约为1.9;
②该函数的一条性质:该函数没有最大值也没有最小值;
6.小明根据学习函数的经验,对函数y=+1的图象与性质进行了探究.下面是小明的探究过程,请补充完整:21教育网
(1)函数y=+1的自变量x的取值范围是 ;
(2)下表列出了y与x的几组对应值,请写出m,n的值:m= ,n= ;
x … ﹣ ﹣1 ﹣ 0
2
3
…
y …
m
0 ﹣1 n 2
…
(3)在如图所示的平面直角坐标系中,描全上表中以各对对应值为坐标的点,并画出该函数的图象.
(4)结合函数的图象,解决问题:
①写出该函数的一条性质:
②当函数值+1>时,x的取值范围是:
③方程+1=x的解为:
【答案】(1)x≠1;(2),3;(3)见解析;(4)①函数图象经过原点且关于点(1,1)对称,②1<x<3,③x=0或x=221·cn·jy·com
【详解】
解:(1)由分式的分母不为0得:x﹣1≠0,
∴x≠1;
故答案为:x≠1.
(2)当x=﹣1时,y=+1=,
当x=时,y=+1=3,
∴m=,n=3,
故答案为:,3.
(3)如图:
(4)①观察函数图象,可知:函数图象经过原点且关于点(1,1)对称,
故答案为:函数图象经过原点且关于点(1,1)对称.
②观察函数图象,可知:当函数值+1>时,x的取值范围是1<x<3,
故答案为:1<x<3.
③观察函数图象可知:方程+1=x的解为x=0或x=2,
故答案为:x=0或x=2.
_21?????????è?????(www.21cnjy.com)_
突破08:“个性函数图像”满分计划
1.小亮在学习中遇到这样一个问题:
如图,点是弧上一动点,线段点是线段的中点,过点作,交的延长线于点.当为等腰三角形时,求线段的长度.2·1·c·n·j·y
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题,请将下面的探究过程补充完整:【来源:21·世纪·教育·网】
根据点在弧上的不同位置,画出相应的图形,测量线段的长度,得到下表的几组对应值.
操作中发现:
①"当点为弧的中点时, ".则上中的值是
②"线段的长度无需测量即可得到".请简要说明理由;
将线段的长度作为自变量和的长度都是的函数,分别记为和,并在平面直角坐标系中画出了函数的图象,如图所示.请在同一坐标系中画出函数的图象;
继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当为等腰三角形时,线段长度的近似值.(结果保留一位小数).21·世纪*教育网
【答案】(1)①5.0;②见解析;(2)图象见解析;(3)图象见解析;3.5cm或5.0cm或6.3cm;
【分析】
(1)①点为弧的中点时,△ABD≌△ACD,即可得到CD=BD;②由题意得△ACF≌△ABD,即可得到CF=BD;21*cnjy*com
(2)根据表格数据运用描点法即可画出函数图象;
(3)画出的图象,当为等腰三角形时,分情况讨论,任意两边分别相等时,即任意两个函数图象相交时的交点横坐标即为BD的近似值.【来源:21cnj*y.co*m】
【详解】
解:(1)①点为弧的中点时,由圆的性质可得:
,
∴△ABD≌△ACD,
∴CD=BD=5.0,
∴;
②∵,
∴,
∵,
∴△ACF≌△ABD,
∴CF=BD,
∴线段的长度无需测量即可得到;
(2)函数的图象如图所示:
(3)由(1)知,
画出的图象,如上图所示,当为等腰三角形时,
①,BD为与函数图象的交点横坐标,即BD=5.0cm;
②,BD为与函数图象的交点横坐标,即BD=6.3cm;
③,BD为与函数图象的交点横坐标,即BD=3.5cm;
综上:当为等腰三角形时,线段长度的近似值为3.5cm或5.0cm或6.3cm.
2.有这样一个问题:探究函数的图象与性质.下面是小文的探究过程,请补充完整:
(1)函数的自变量的取值范围是__________;
(2)下表是与的几组对应值:
如图,在平面直角坐标系中,描出了以上表中各对应值为坐标的点.
①观察图中各点的位置发现:点和,和,和,和均关于某点中心对称,则该点的坐标为__________;【出处:21教育名师】
②小文分析函数表达式发现:当时,该函数的最大值为0,则该函数图象在直线左侧的最高点的坐标为__________;【版权所有:21教育】
(3)小文补充了该函数图象上两个点,.
①在上图中描出这两个点,并画出该函数的图象;
②写出该函数的一条性质:__________.
【答案】(1)x≠1;(2)①(1,1);②(0,0);(3)①作图见解析;②当x<0时,y随x的增大而增大(答案不唯一).21教育名师原创作品
【解析】
【分析】
(1)分式的分母不等于零;
(2)①根据中心对称的性质和所对应的点点坐标即可求得,
②根据函数的性质求得即可;
(3)①根据坐标系中的点,用平滑的直线连接即可;
②可以从增减性、渐近性、连续性、与坐标轴交点、图象所在象限等方面作答.
【详解】
解:(1)依题意得:2x-2≠0,
解得x≠1,
故答案是:x≠1;
(2)①点A1和B1,A2和B2,A3和B3,A4和B4均关于某点中心对称,B1(0,0),A1(2,2),
∴中心点点坐标为(1,1);
②∵当x<1时,该函数的最大值为0,
∴该函数图象在直线x=1左侧的最高点的坐标为(0,0);
故答案为(1,1);(0,0);
(3)①
②该函数的性质:
(ⅰ)当x<0时,y随x的增大而增大;
当0≤x<1时,y随x的增大而减小;
当1<x<2时,y随x的增大而减小;
当x≥2时,y随x的增大而增大.
(ⅱ)函数的图象经过第一、三、四象限.
(ⅲ)函数的图象与直线x=1无交点,图象由两部分组成.
故答案为当x<0时,y随x的增大而增大(答案不唯一);
3.如图1,在四边形中,对角线平分.为了研究图中线段之间的数量关系,设.
(1)由题意可得,(在括号内填入图1中相应的线段)y关于x的函数表达式为________;
(2)如图2,在平面直角坐标系中,根据(1)中y关于x的函数表达式描出了其图象上的一部分点,请依据描出的点画出该函数的图象;21世纪教育网版权所有
(3)结合函数图象,解决问题:
①写出该函数的一条性质:__________________________;
②估计的最小值为__________.(结果精确到0.1)
【答案】(1),.(2)图见解析(3)①当时,y随x的增大而增大(答案不唯一). ②4.8.
【分析】
(1)通过证明△ABC∽△ACD,得到,再把相关数据代入求解即可;
(2)用平滑的曲线将平面直角坐标系上的点连接起来即可;
(3)观察图象,写出其性质即可;
(4)观察图象,找出y的最小值对应的x,即可求出AB+AD的最小值.
【详解】
(1)∵平分,
∴
又∵,
∴△ABC∽△ACD
∴,
∵
∴
∴
∴
故答案为:,.
(2)如图所示:
(3)①当时,y随x的增大而增大(答案不唯一).
故答案为:当时,y随x的增大而增大(答案不唯一).
②AB+AD=x+
观察图象可得,y有最小值时,x约为0.7,
故AB+AD的最小值约为:x+=0.7+
故答案为:4.8.
4.有这样一个问题,探究函数y=x2﹣2的图象与性质,小张根据学习函数的经验,对函数y=x2﹣2的图象与性质进行了研究,下面是小张的探究过程,请补充完整:
(1)函数y=x2﹣2的自变量取值范围是 .
(2)下表是y与x的几组对应值:
x … ﹣4 ﹣3 ﹣2 ﹣1 0 1 2 3 4
y … n 3 0 ﹣1 0 ﹣1 0 3 m
求m的值;
(3)如图,在平面直角坐标系xOy中,算出了以上表中各对对应值为坐标的点,根据算出的点,画出该函数的图象;www.21-cn-jy.com
(4)进一步探究发现,该函数图象在第四象限内的最低点是(1,﹣1),结合函数的图象,写出该函数的其他性质(一条即可);www-2-1-cnjy-com
(5)根据图象回答:方程x2﹣2=﹣有 个实数解.
【答案】(1)自变量取值范围是任意实数;(2)m的值为8;(3)如图见解析;(4)当x<﹣1时,y随x的增大而减小.(5)方程x2﹣2=﹣有3个实数解.2-1-c-n-j-y
【分析】
(1)根据二次根式的意义和函数关系式即可求解;
(2)根据函数关系式将x的值代入即可求解;
(3)根据表格数据,描点,连线,即可画出图象;
(4)观察函数图像,利用增减性写出一条性质;
(5)根据图象将y=x2-2的图象向下平移0.5个单位长度与原函数图象有三个交点即可求解.
【详解】
(1)根据函数解析式可知:无论x为何值,均有意义,
∴自变量取值范围是任意实数.
故答案为任意实数.
(2)当x=4时,y=.
答:m的值为8.
(3)如图:
(4)根据函数图象可知:
当x<﹣1时,y随x的增大而减小.
(5)根据图象可知:
直线y=﹣,与函数图象有三个交点,即可得:
方程x2﹣2=﹣有3个实数解.
5.有这样一个问题:探究函数的图象与性质.
小菲根据学习函数的经验,对函数的图象与性质进行了探究.
下面是小菲的探究过程,请补充完整:
(1)函数的自变量的取值范围是___________________.
(2)下表是与的几组对应值.
…
1 2 3 …
…
2
…
表中的值为____________________________.
(3)如下图,在平面直角坐标系中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;
(4)根据画出的函数图象,写出:
①时,对应的函数值约为__________________(结果保留一位小数);
②该函数的一条性质:________________________________________________________.
【答案】(1);(2);(3)图像见详解;(4)①1.9;②该函数的一条性质:该函数没有最大值也没有最小值(答案不唯一);21cnjy.com
解:(1)函数的自变量的取值范围是;
(2)根据图表可知当时的函数值为m,把代入,
得:,
∴;
(3)函数图像如下图示:
;
(4)①由(3)中的函数图像可知,当时,对应的函数值约为1.9;
②该函数的一条性质:该函数没有最大值也没有最小值;
6.小明根据学习函数的经验,对函数y=+1的图象与性质进行了探究.下面是小明的探究过程,请补充完整:21教育网
(1)函数y=+1的自变量x的取值范围是 ;
(2)下表列出了y与x的几组对应值,请写出m,n的值:m= ,n= ;
x … ﹣ ﹣1 ﹣ 0
2
3
…
y …
m
0 ﹣1 n 2
…
(3)在如图所示的平面直角坐标系中,描全上表中以各对对应值为坐标的点,并画出该函数的图象.
(4)结合函数的图象,解决问题:
①写出该函数的一条性质:
②当函数值+1>时,x的取值范围是:
③方程+1=x的解为:
【答案】(1)x≠1;(2),3;(3)见解析;(4)①函数图象经过原点且关于点(1,1)对称,②1<x<3,③x=0或x=221·cn·jy·com
【详解】
解:(1)由分式的分母不为0得:x﹣1≠0,
∴x≠1;
故答案为:x≠1.
(2)当x=﹣1时,y=+1=,
当x=时,y=+1=3,
∴m=,n=3,
故答案为:,3.
(3)如图:
(4)①观察函数图象,可知:函数图象经过原点且关于点(1,1)对称,
故答案为:函数图象经过原点且关于点(1,1)对称.
②观察函数图象,可知:当函数值+1>时,x的取值范围是1<x<3,
故答案为:1<x<3.
③观察函数图象可知:方程+1=x的解为x=0或x=2,
故答案为:x=0或x=2.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
