专题01 折叠三件套满分计划-备战2022年中考数学之满分专题专题训练(含解析)
文档属性
| 名称 | 专题01 折叠三件套满分计划-备战2022年中考数学之满分专题专题训练(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 21:18:16 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
突破01:“折叠三件套”满分计划
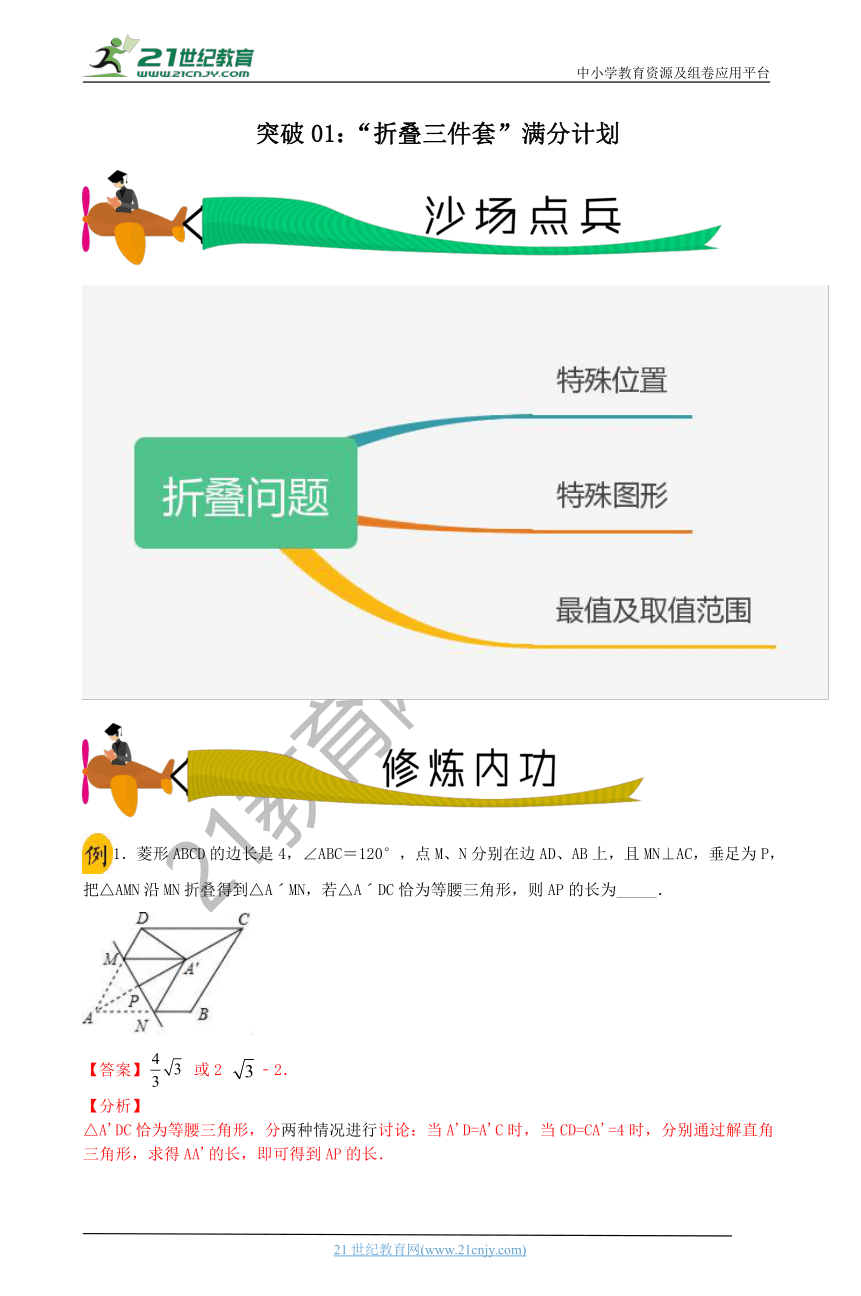
1.菱形ABCD的边长是4,∠ABC=120°,点M、N分别在边AD、AB上,且MN⊥AC,垂足为P,把△AMN沿MN折叠得到△AˊMN,若△AˊDC恰为等腰三角形,则AP的长为_____.
【答案】 或2 ﹣2.
【分析】
△A'DC恰为等腰三角形,分_??¤?§???????è??è??_讨论:当A'D=A'C时,当CD=CA'=4时,分别通过解直角三角形,求得AA'的长,即可得到AP的长.21cnjy.com
【详解】
如图,当A’D’=AC时,∠A’DC=∠A’CD=30?,
∴∠AA’D=60?,
又∵∠CAD=30?,
∴∠ADA’=30?,
∴Rt△ADA’中,
由折叠可得,AP=;
如图,当CD=CA’=4时,连接BD交AC于O,则
再Rt△COD中,,
∴AC=,
∴,
由折叠可得, ;
故答案为或2﹣2.
2.如图,在矩形ABCD中,,,点E在边BC上,且.连接AE,将沿AE折叠,若点B的对应点落在矩形ABCD的边上,则 a的值为________.
【答案】或
【分析】
分两种情况:①点落在AD边上,根据矩形与折叠的性质易得,即可求出a的值;②点落在CD边上,证明,根据相似三角形对应边成比例即可求出a的值.
【详解】
解:分两种情况:
①当点落在AD边上时,如图1.
四边形ABCD是矩形,
,
将沿AE折叠,点B的对应点落在AD边上,
,
,
,
;
②当点落在CD边上时,如图2.
∵四边形ABCD是矩形,
,.
将沿AE折叠,点B的对应点落在CD边上,
,,,
,.
在与中,
,
,
,即,
解得,(舍去).
综上,所求a的值为或.
故答案为或.
3.如图,在矩形中,,为中点,点为上一动点,将沿所在直线折叠到的位置,连接,则的最小值为__________.
【答案】
【分析】
由题意可知当点G在DE上时,此时GD的值最小,根据勾股定理求出DE,根据折叠的性质可知GE=BE,即可求出GD的最小值.21·cn·jy·com
【详解】
解:如图所示,
由EG=EB==,可得当点G在DE上时,此时GD的值最小,
根据折叠的性质,△EBF≌△EGF,
∴EG⊥GF,
∴EG=EB,
∵E是AB边的中点,AB=5,
∴AE=EG=,
∵BC=AD=12,
∴Rt△ADE中,DE=,
∴GD=.
故答案为:.
4.如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为_____.2·1·c·n·j·y
【答案】或4
【解析】
分析:当△A′EF为直角三角形时,存在两种情况:
①当∠A'EF=90°时,如图_1?????????????§°_的性质和平行线可得:A'C=A'E=4,根据直角三角形斜边中线的性质得:BC=2A'B=8,最后利用勾股定理可得AB的长;【来源:21·世纪·教育·网】
②当∠A'FE=90°时,如图2,证明△ABC是等腰直角三角形,可得AB=AC=4.
详解:当△A′EF为直角三角形时,存在两种情况:
①当∠A'EF=90°时,如图1,
.
∵△A′BC与△ABC关于BC所在直线对称,
∴A'C=AC=4,∠ACB=∠A'CB,
∵点D,E分别为AC,BC的中点,
∴D、E是△ABC的中位线,
∴DE∥AB,
∴∠CDE=∠MAN=90°,
∴∠CDE=∠A'EF,
∴AC∥A'E,
∴∠ACB=∠A'EC,
∴∠A'CB=∠A'EC,
∴A'C=A'E=4,
Rt△A'CB中,∵E是斜边BC的中点,
∴BC=2A'E=8,
由勾股定理得:AB2=BC2-AC2,
∴AB=;
②当∠A'FE=90°时,如图2,
.
∵∠ADF=∠A=∠DFB=90°,
∴∠ABF=90°,
∵△A′BC与△ABC关于BC所在直线对称,
∴∠ABC=∠CBA'=45°,
∴△ABC是等腰直角三角形,
∴AB=AC=4;.
综上所述,AB的长为4或4;
故答案为4或4.
5.如图,中,,,点,分别在边,上,且,连接,点是的中点,点是的中点,线段的长为______.
【答案】
【分析】
如图,作CH∥AB,连接DN,_???é??DN??¤C_H于H,连接EH,作CJ⊥EH于J.首先证明CH=EC,∠ECH=120°,解直角三角形求出EH,利用三角形中位线定理即可解决问题.21世纪教育网版权所有
【详解】
解:如图,作CH∥AB,连接DN,延长DN交CH于H,连接EH,作CJ⊥EH于J.
∵BD∥CH,
∴∠B=∠NCH,
∵BN=CN,∠DNB=∠KNC,
∵△DNB≌△HNC(ASA),
∴BD=CH,DN=NH,
∵BD=EC=2,
∴EC=CH=2,
∵∠A+∠ACH=180°,∠A=60°,
∴∠ECH=120°,
∵CJ⊥EH,
∴EJ=JH=EC?cos30°=
∴EH=2EJ=2,
∵DM=ME,DN=NH,
∴MN=EH=.
故答案为.
6.如图,在中,,,,点,分别是边,上的动点,沿所在的直线折叠,使点的对应点始终落在边上.若为直角三角形,则的长为_________.www.21-cn-jy.com
【答案】1或.
【解析】
试题分析:在中,,,可得∠B=∠C=45°,由折叠可知,BM= ,若使为直角三角形,分两种情况:①,由∠C=45°可得=,设BM=x,则==x,MC=,所以x+=,解得x=1,即BM=1;②,此时点B和点C重合,BM=.所以BM的长为1或.21·世纪*教育网
7.如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为_____.www-2-1-cnjy-com
【答案】或
【分析】
分类讨论当MB_??????2??????M_B′=1时分别求解,在△EN B′中,设EN=x,根据勾股定理,表示出EB′的值,再根据△EN B′与△B′MA相似,列出等量关系,可得EN的长,再根据勾股定理,即可得出答案.2-1-c-n-j-y
【详解】
解:如图,由翻折的性质得
AB=AB′,BE=B′E.∠A B′E=∠ABE=90°
∵点B′为线段MN的三等分点
∴①当MB′=2,B′N=1时,设EN=x,得
B′E=.
又∠A B′E=∠ABE=90°
∴∠EB′N+∠M B′A=90°
又∠M B′A+∠M AB′=90°
∴∠EB′N= M AB′
∴△B′EN∽△AB′M,
∴ = ,即=,
∴x2=,
∴BE=B′E== .
②当MB′=1,B′N=2时,设EN=x,得
B′E=,
同①可得△B′EN∽△AB′M,
∴ =,即 = ,
解得x2=,BE=B′E==,
故答案为:或.
8.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=2,BD平分∠ABC,点E是边AB上一动点(不与A、B重合),沿DE所在的直线折叠∠A,点A的对应点为F,当△BFC是直角三角形且BC为直角边时,则AE的长为_____.21教育网
【答案】或
【分析】
分两种情况,当∠BCF=90°时,点F落在AC的延长线上,当∠CBF=90°时,画出图形,由直角三角形的性质可求出答案.21*cnjy*com
【详解】
解:∵∠ACB=90°,∠A=30°,AB=2,
∴BC=AB=,
∴AC=3,
∵BD平分∠ABC,
∴∠CBD=30°,
∴CD=BC?tan30°==1,
∴BD=AD=2,
如图1,当∠BCF=90°时,点F落在AC的延长线上,
∴∠ADE=90°,
∴AE=.
如图2,当∠CBF=90°,DF=DA=DB,
∵∠ACB=∠CBF=90°,
∴BF∥AC,
∴∠DFB=∠DBF=∠ADF=∠BDC=60°,
∵∠ADE=∠EDF,
∴∠ADE=∠A=30°,
∴AE=DE,
过点E作EM⊥AD于点M,
∵AD=2,
∴AM=1,
∴AE=.
故答案为:或.
_21?????????è?????(www.21cnjy.com)_
突破01:“折叠三件套”满分计划
1.菱形ABCD的边长是4,∠ABC=120°,点M、N分别在边AD、AB上,且MN⊥AC,垂足为P,把△AMN沿MN折叠得到△AˊMN,若△AˊDC恰为等腰三角形,则AP的长为_____.
【答案】 或2 ﹣2.
【分析】
△A'DC恰为等腰三角形,分_??¤?§???????è??è??_讨论:当A'D=A'C时,当CD=CA'=4时,分别通过解直角三角形,求得AA'的长,即可得到AP的长.21cnjy.com
【详解】
如图,当A’D’=AC时,∠A’DC=∠A’CD=30?,
∴∠AA’D=60?,
又∵∠CAD=30?,
∴∠ADA’=30?,
∴Rt△ADA’中,
由折叠可得,AP=;
如图,当CD=CA’=4时,连接BD交AC于O,则
再Rt△COD中,,
∴AC=,
∴,
由折叠可得, ;
故答案为或2﹣2.
2.如图,在矩形ABCD中,,,点E在边BC上,且.连接AE,将沿AE折叠,若点B的对应点落在矩形ABCD的边上,则 a的值为________.
【答案】或
【分析】
分两种情况:①点落在AD边上,根据矩形与折叠的性质易得,即可求出a的值;②点落在CD边上,证明,根据相似三角形对应边成比例即可求出a的值.
【详解】
解:分两种情况:
①当点落在AD边上时,如图1.
四边形ABCD是矩形,
,
将沿AE折叠,点B的对应点落在AD边上,
,
,
,
;
②当点落在CD边上时,如图2.
∵四边形ABCD是矩形,
,.
将沿AE折叠,点B的对应点落在CD边上,
,,,
,.
在与中,
,
,
,即,
解得,(舍去).
综上,所求a的值为或.
故答案为或.
3.如图,在矩形中,,为中点,点为上一动点,将沿所在直线折叠到的位置,连接,则的最小值为__________.
【答案】
【分析】
由题意可知当点G在DE上时,此时GD的值最小,根据勾股定理求出DE,根据折叠的性质可知GE=BE,即可求出GD的最小值.21·cn·jy·com
【详解】
解:如图所示,
由EG=EB==,可得当点G在DE上时,此时GD的值最小,
根据折叠的性质,△EBF≌△EGF,
∴EG⊥GF,
∴EG=EB,
∵E是AB边的中点,AB=5,
∴AE=EG=,
∵BC=AD=12,
∴Rt△ADE中,DE=,
∴GD=.
故答案为:.
4.如图,∠MAN=90°,点C在边AM上,AC=4,点B为边AN上一动点,连接BC,△A′BC与△ABC关于BC所在直线对称,点D,E分别为AC,BC的中点,连接DE并延长交A′B所在直线于点F,连接A′E.当△A′EF为直角三角形时,AB的长为_____.2·1·c·n·j·y
【答案】或4
【解析】
分析:当△A′EF为直角三角形时,存在两种情况:
①当∠A'EF=90°时,如图_1?????????????§°_的性质和平行线可得:A'C=A'E=4,根据直角三角形斜边中线的性质得:BC=2A'B=8,最后利用勾股定理可得AB的长;【来源:21·世纪·教育·网】
②当∠A'FE=90°时,如图2,证明△ABC是等腰直角三角形,可得AB=AC=4.
详解:当△A′EF为直角三角形时,存在两种情况:
①当∠A'EF=90°时,如图1,
.
∵△A′BC与△ABC关于BC所在直线对称,
∴A'C=AC=4,∠ACB=∠A'CB,
∵点D,E分别为AC,BC的中点,
∴D、E是△ABC的中位线,
∴DE∥AB,
∴∠CDE=∠MAN=90°,
∴∠CDE=∠A'EF,
∴AC∥A'E,
∴∠ACB=∠A'EC,
∴∠A'CB=∠A'EC,
∴A'C=A'E=4,
Rt△A'CB中,∵E是斜边BC的中点,
∴BC=2A'E=8,
由勾股定理得:AB2=BC2-AC2,
∴AB=;
②当∠A'FE=90°时,如图2,
.
∵∠ADF=∠A=∠DFB=90°,
∴∠ABF=90°,
∵△A′BC与△ABC关于BC所在直线对称,
∴∠ABC=∠CBA'=45°,
∴△ABC是等腰直角三角形,
∴AB=AC=4;.
综上所述,AB的长为4或4;
故答案为4或4.
5.如图,中,,,点,分别在边,上,且,连接,点是的中点,点是的中点,线段的长为______.
【答案】
【分析】
如图,作CH∥AB,连接DN,_???é??DN??¤C_H于H,连接EH,作CJ⊥EH于J.首先证明CH=EC,∠ECH=120°,解直角三角形求出EH,利用三角形中位线定理即可解决问题.21世纪教育网版权所有
【详解】
解:如图,作CH∥AB,连接DN,延长DN交CH于H,连接EH,作CJ⊥EH于J.
∵BD∥CH,
∴∠B=∠NCH,
∵BN=CN,∠DNB=∠KNC,
∵△DNB≌△HNC(ASA),
∴BD=CH,DN=NH,
∵BD=EC=2,
∴EC=CH=2,
∵∠A+∠ACH=180°,∠A=60°,
∴∠ECH=120°,
∵CJ⊥EH,
∴EJ=JH=EC?cos30°=
∴EH=2EJ=2,
∵DM=ME,DN=NH,
∴MN=EH=.
故答案为.
6.如图,在中,,,,点,分别是边,上的动点,沿所在的直线折叠,使点的对应点始终落在边上.若为直角三角形,则的长为_________.www.21-cn-jy.com
【答案】1或.
【解析】
试题分析:在中,,,可得∠B=∠C=45°,由折叠可知,BM= ,若使为直角三角形,分两种情况:①,由∠C=45°可得=,设BM=x,则==x,MC=,所以x+=,解得x=1,即BM=1;②,此时点B和点C重合,BM=.所以BM的长为1或.21·世纪*教育网
7.如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为_____.www-2-1-cnjy-com
【答案】或
【分析】
分类讨论当MB_??????2??????M_B′=1时分别求解,在△EN B′中,设EN=x,根据勾股定理,表示出EB′的值,再根据△EN B′与△B′MA相似,列出等量关系,可得EN的长,再根据勾股定理,即可得出答案.2-1-c-n-j-y
【详解】
解:如图,由翻折的性质得
AB=AB′,BE=B′E.∠A B′E=∠ABE=90°
∵点B′为线段MN的三等分点
∴①当MB′=2,B′N=1时,设EN=x,得
B′E=.
又∠A B′E=∠ABE=90°
∴∠EB′N+∠M B′A=90°
又∠M B′A+∠M AB′=90°
∴∠EB′N= M AB′
∴△B′EN∽△AB′M,
∴ = ,即=,
∴x2=,
∴BE=B′E== .
②当MB′=1,B′N=2时,设EN=x,得
B′E=,
同①可得△B′EN∽△AB′M,
∴ =,即 = ,
解得x2=,BE=B′E==,
故答案为:或.
8.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=2,BD平分∠ABC,点E是边AB上一动点(不与A、B重合),沿DE所在的直线折叠∠A,点A的对应点为F,当△BFC是直角三角形且BC为直角边时,则AE的长为_____.21教育网
【答案】或
【分析】
分两种情况,当∠BCF=90°时,点F落在AC的延长线上,当∠CBF=90°时,画出图形,由直角三角形的性质可求出答案.21*cnjy*com
【详解】
解:∵∠ACB=90°,∠A=30°,AB=2,
∴BC=AB=,
∴AC=3,
∵BD平分∠ABC,
∴∠CBD=30°,
∴CD=BC?tan30°==1,
∴BD=AD=2,
如图1,当∠BCF=90°时,点F落在AC的延长线上,
∴∠ADE=90°,
∴AE=.
如图2,当∠CBF=90°,DF=DA=DB,
∵∠ACB=∠CBF=90°,
∴BF∥AC,
∴∠DFB=∠DBF=∠ADF=∠BDC=60°,
∵∠ADE=∠EDF,
∴∠ADE=∠A=30°,
∴AE=DE,
过点E作EM⊥AD于点M,
∵AD=2,
∴AM=1,
∴AE=.
故答案为:或.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
