专题02 最值问题之五大终极策略-备战2022年中考数学之满分专题专题训练(含解析)
文档属性
| 名称 | 专题02 最值问题之五大终极策略-备战2022年中考数学之满分专题专题训练(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 21:20:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
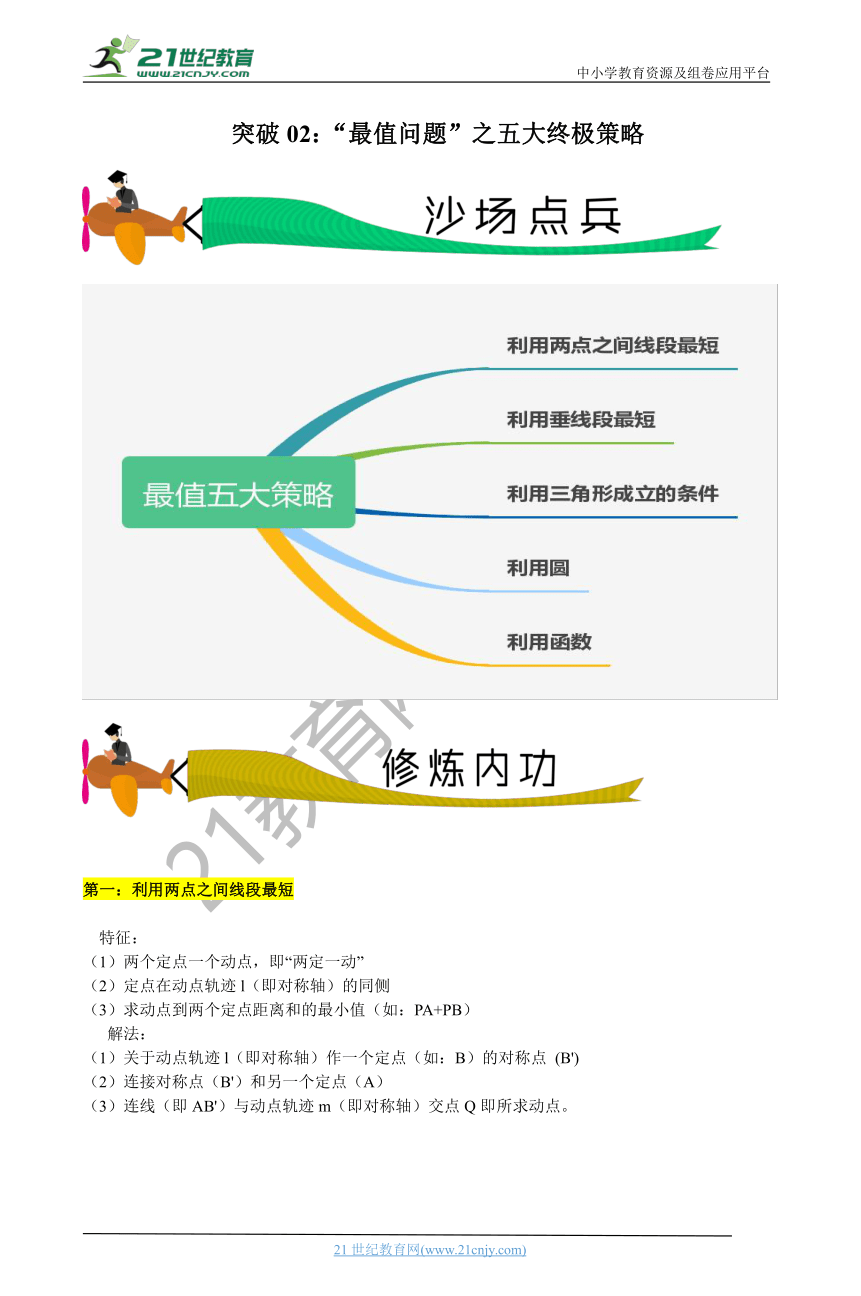
突破02:“最值问题”之五大终极策略
第一:利用两点之间线段最短
特征:
(1)两个定点一个动点,即“两定一动”
(2)定点在动点轨迹l(即对称轴)的同侧
(3)求动点到两个定点距离和的最小值(如:PA+PB)
解法:
(1)关于动点轨迹l(即对称轴)作一个定点(如:B)的对称点 (B')
(2)连接对称点(B')和另一个定点(A)
(3)连线(即AB')与动点轨迹m(即对称轴)交点Q即所求动点。
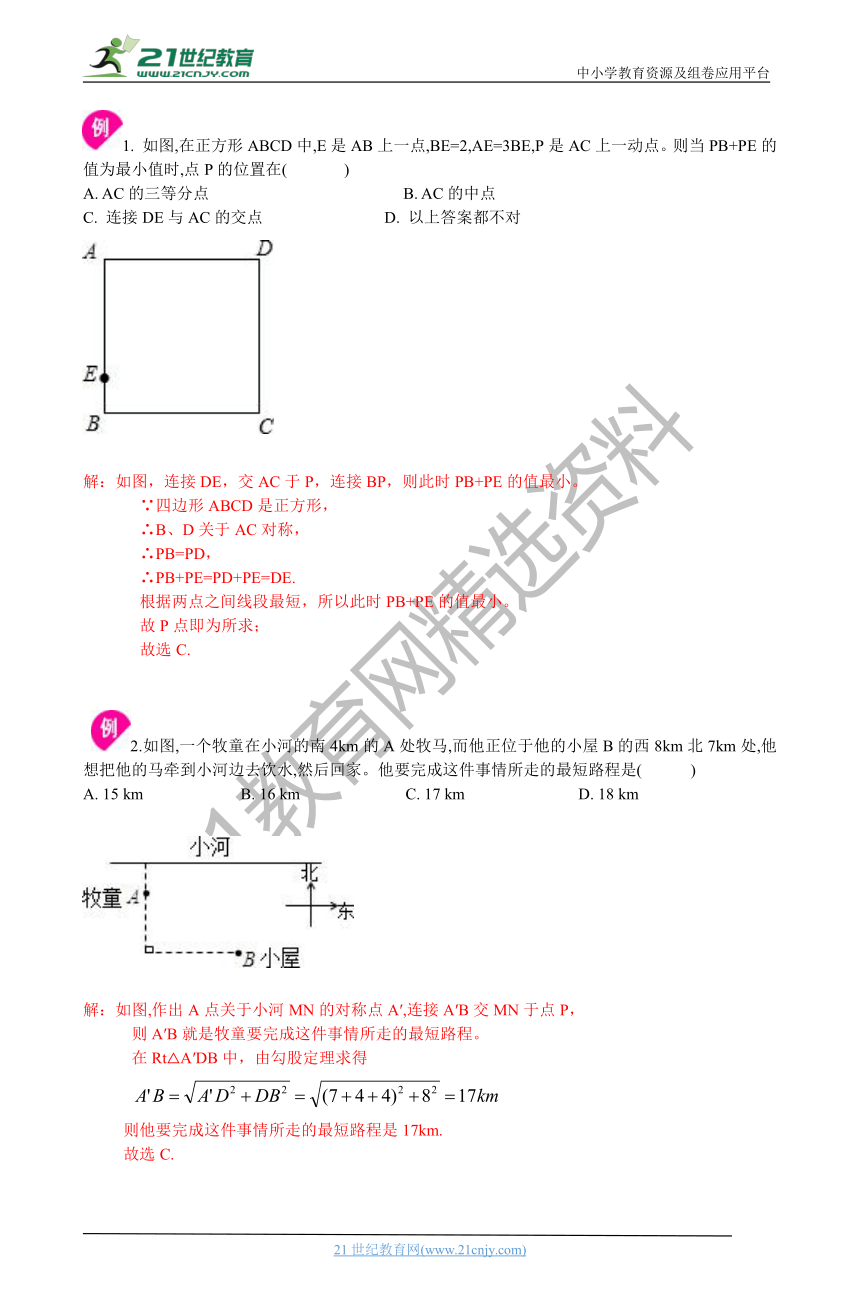
1. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点。则当PB+PE的值为最小值时,点P的位置在( )21世纪教育网版权所有
A. AC的三等分点 B. AC的中点
C. 连接DE与AC的交点 D. 以上答案都不对
解:如图,连接DE,交AC于P,连接BP,则此时PB+PE的值最小。
∵四边形ABCD是正方形,
∴B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE=DE.
根据两点之间线段最短,所以此时PB+PE的值最小。
故P点即为所求;
故选C.
2.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家。他要完成这件事情所走的最短路程是( )
A. 15 km B. 16 km C. 17 km D. 18 km
解:如图,作出A点关于小河MN的对称点A′,连接A′B交MN于点P,
则A′B就是牧童要完成这件事情所走的最短路程。
在Rt△A′DB中,由勾股定理求得
则他要完成这件事情所走的最短路程是17km.
故选C.
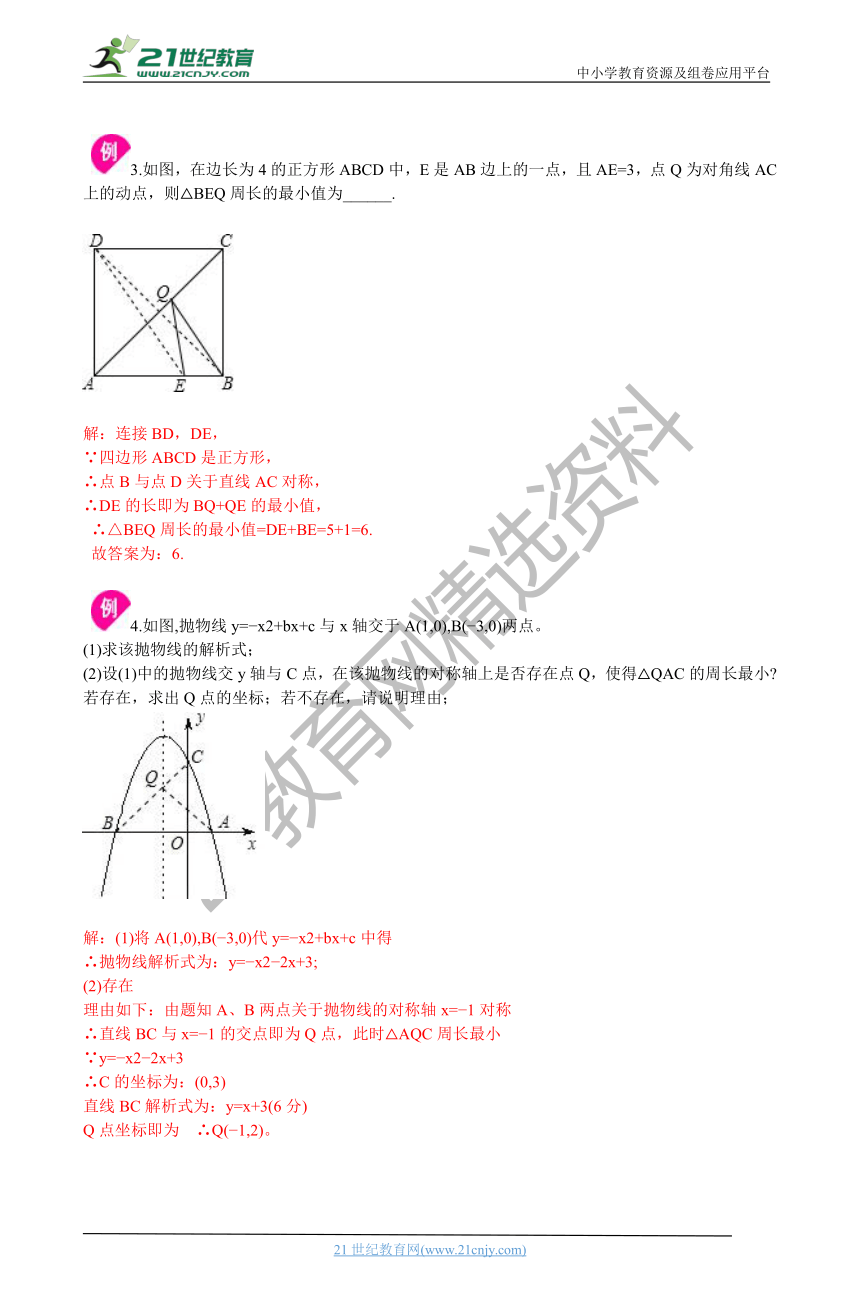
3.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为______.21·cn·jy·com
解:连接BD,DE,
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,
∴DE的长即为BQ+QE的最小值,
∴△BEQ周长的最小值=DE+BE=5+1=6.
故答案为:6.
4.如图,抛物线y=?x2+bx+c与x轴交于A(1,0),B(?3,0)两点。
(1)求该抛物线的解析式;
(2)设(1)中的_???????????¤yè??_与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;21·世纪*教育网
解:(1)将A(1,0),B(?3,0)代y=?x2+bx+c中得
∴抛物线解析式为:y=?x2?2x+3;
(2)存在
理由如下:由题知A、B两点关于抛物线的对称轴x=?1对称
∴直线BC与x=?1的交点即为Q点,此时△AQC周长最小
∵y=?x2?2x+3
∴C的坐标为:(0,3)
直线BC解析式为:y=x+3(6分)
Q点坐标即为 ∴Q(?1,2)。
第二:利用垂线段最短
(1)点P是∠AOB的内部_??????????????¨O_A上找一点M,在OB上找一点N,使得PN+MN最小.要PN+MN最小,设法将PN,MN转化在同一条直线上,想到作点P关于OB的对称点P′,即求P′N+MN的最小值,因此只要P′M⊥OA,利用垂线段最短即可求解.www-2-1-cnjy-com
(2)“胡不归”问题即点P在直线BM上运动的“PA+k·PB(0如图①,已知sin∠MBN=k_??????P??????M_BN其中一边BM上的一个动点,点A在射线BM、BN的同侧,连接AP,则当“PA+k·PB”的值最小时,P点的位置如何确定?2-1-c-n-j-y
分析:本模型的关_é????¨????????????_定“k·PB”的大小,如图②,过点P作PQ⊥BN于点Q,则k·PB=PB·sin∠MBN=PQ,∴求“PA+k·PB”的最小值转化为求“PA+PQ”的最小值问题,即当A、P、Q三点共线时“PA+k·PB”的值最小(如图③),此时AQ⊥BN,利用垂线段最短求解即可.
特殊情况:当求PA+PB的最小值时,题干中∠MBN的度数一般为30°;当求PA+PB的最小值时,题干中∠MBN的度数一般为45°;当求PA+PB的最小值时,题干中∠MBN的度数一般为60°.【来源:21cnj*y.co*m】
5.如图,在锐角△ABC中,BC=4,∠ABC=45°,BD平分∠ABC,M,N分别是BD、BC上的动点,则CM+MN的最小值是________.【出处:21教育名师】
6.如图,菱形ABCD的边长为3,∠ABC=60°,P是对角线BD上的一个动点,则BP+PC的最小值是( )21教育名师原创作品
7.如图,在Rt△ABC中,∠BAC=90°,且AB=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为________.
解:如解图,连接AD,∵∠_BAC???90_°,DM⊥AB,DN⊥AC,∴四边形AMDN是矩形,∴MN=AD,∴当线段AD最短时,MN最短,即当AD为BC边上的高时,AD最短,在Rt△ABC中,BC==5,S△ABC=×AB·AC=×BC·AD,∴×3×4=×5·AD,∴AD=.∴线段MN的最小值为.
8.如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是________.
解:如解图,过点D作DF⊥_AB??????F???_过点C作CQ⊥AB于点Q,易证△BDF∽△BAE,则∠BDF=∠A,∴tan∠BDF=tanA=2.∴=2.设DF=x,则BF=2x,在Rt△BDF中,BD==x,∴cos∠BDF=.∴DF=BD·cos∠BDF=BD.∴CD+BD=CD+DF.∴CD+BD的最小值即为点C到AB的垂线段CQ的长度, 在Rt△AEB中,tanA=2,AB=10,∴BE=4,又∵AB=AC,∴△ACQ≌△ABE.∴CQ=BE=4.
第三:利用三角形成立的条件求最值
(1)同侧差最大值问题
如图,两定点A、B位于直线l同侧,在直线l上找一点P,使得|PA-PB|的值最大
方法:根据三角形任意两边之差_?°??????????è?????_|PA-PB|<AB,则|PA-PB|的最大值为线段AB的长.连接AB并延长,与直线l的交点即为点Pwww.21-cn-jy.com
(2)异侧差最大值问题
如图,两定点A、B位于直线l异侧,在直线l上找一点P,使得|PA-PB|的值最大
方法:将异侧点转化为同侧,同③即可解决.作点B关于直线l的对称点B′,连接AB′并延长,与直线l的交点即为点P
9.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为________
解析:因为AB为定长,所以取其中_???E??????OE_为定值,在△ODE中,DE为定值,OE为定值,根据三角形三边关系即可得到OD的最大值。即:O,D,E在一直线上OD最大
10..如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6,P为对角线BD上一点,则PM-PN的最大值为________.
解:如解图,∵四边形AB_CD????????????_,∴AB和CB关于对角线BD对称,作点M关于BD对称的点M′,则点M′在AB上,连接PM′、M′N,根据对称可得BM′=BM=6,又∵AB=8,∴AC=8,AM′=2,AN=AO=×AC=2,∵cos∠M′AN=cos45°==,∴∠AM′N=90°,∴M′N=AM′=2,∵PM-PN=PM′-PN≤M′N=2,∴当点P运动到P′时,即点M′、N、P′共线时,PM-PN=PM′-PN=M′N=2,∴PM-PN的最大值为2.【来源:21·世纪·教育·网】
11.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C顺时针旋转得到△A′B′C,D是A′B′的中点,连接BD,若BC=2,∠ABC=60°,则线段BD的最大值为________
解:如解图,连接CD,在R_t???ABC???_,∵∠ACB=90°,BC=2,∠ABC=60°,∴∠A=30°,∴A′B′=AB=2BC=4,∵DB′=DA′,∴CD=A′B′=2,∴BD≤CD+CB=4,∴BD的最大值为4.
第四:利用圆求最值
12.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=6,点D是AB上一动点,将△BCD沿CD所在直线折叠,使点B落在点P处,连接AP,则线段AP的最小值为 ( C )
21*cnjy*com
A. B.3
C.3-3 D.3+3
13.如图,在Rt△ABC中,∠ABC=90°,∠C=30°,AB=1,D为线段AC上一动点(不与点A,C重合),将△BDC沿着BD翻折,点C的对应点为F,E为AC的中点.当EF最短时,EF的长为________
答案:-1
14.如图,正方形ABCD的边长为6,点E,F分别从点D,C同时出发,沿着射线DA,射线CD匀速运动(二者速度相等).设直线AF与直线BE交于点H,连接DH,则线段DH的长度的最小值为________
答案:3-3
15.如图,在边长为2的等边三角形ABC中,点D,E分别是边AC,BC上的动点,且BE=CD,连接AE,BD交于点P,则△ABP的面积的最大值为________
2·1·c·n·j·y
答案:
16.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为________
答案:+
利用函数求最值
17.如图,正方形ABCD的边长是1,点M,N分别在BC,CD上,使得△CMN的周长为2,则△MAN的面积最小值为 。【版权所有:21教育】
:21世纪教育网]
解:延长CB至L,使BL=DN,
则Rt△ABL≌Rt△ADN,故AL=AN,
∵CM+CN+MN=2,CN+DN+CM+BM=1+1=2,
∴MN=DN+BM=BL+BM=ML,∴△AMN≌△AML(SSS),
设CM=x,CN=y,MN=z,x2+y2=z2,
∵x+y+z=2,则x=2-y-z,
∴(2-y-z)2+y2=z2,
整理得2y2+(2z-4)y+(4-4z)=0,
即:y2+(z-2)y+(2-2z)=0
∴△=(z-2)2-4(2-2z)≥0,
∴z2+4z-4≥0
又∵z>0,∴z>2-2
又∵z>0,∴z>2-2
∵S△AMN=S△AML=ML?AB=z。
∴当z=2-2时,S△AMN取得最小值,为-1,故答案为:-1。
18.课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm。要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上。问加工成的正方形零件的边长是多少毫米?21*cnjy*com
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题。
(1)如果原题中要加工的零件_??????????????????_且此矩形是由两个并排放置的正方形所组成,如图1所示,此时,这个矩形零件的两条边长又分别为多少毫米?请你计算。
(2)如果原题中所要加_?·????é???????????_一个矩形,如图2所示,这样,此矩形零件的两条边长就不能确定,但这个矩形的面积有最大值,求达到这个最大值时矩形零件的两条边长。
解:(1)设矩形的边长PN=2y(mm),则PQ=y(mm),由条件可得△APN∽△ABC,
∴=,即=,解得y=,
∴PN=×2=(mm)。
答:这个矩形零件的两条边长分别为mm,mm。
(2)设PN=x(mm),由条件可得△APN∽△ABC,21世纪教育网
∴=,即=,
解得PQ=80-x,
∴S=PN?PQ=x(80-x)=-x2+80x=-(x-60)2+2400,
∴S的最大值为2400mm2,此时PN=60mm,PQ=80-×60=40(mm)
19. 如图,P是抛物线y=-x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为 。21教育网
解析:设一条边为自变量x,周长为因变量y,建立函数关系式即可
20.如图,正方形ABCD的边长为4,E、F分别是BC、CD上的两个动点,且AE⊥EF。则AF的最小值是 。21cnjy.com
解析:通过数量关系和位置关系,建立函数关系式即可
_21?????????è?????(www.21cnjy.com)_
突破02:“最值问题”之五大终极策略
第一:利用两点之间线段最短
特征:
(1)两个定点一个动点,即“两定一动”
(2)定点在动点轨迹l(即对称轴)的同侧
(3)求动点到两个定点距离和的最小值(如:PA+PB)
解法:
(1)关于动点轨迹l(即对称轴)作一个定点(如:B)的对称点 (B')
(2)连接对称点(B')和另一个定点(A)
(3)连线(即AB')与动点轨迹m(即对称轴)交点Q即所求动点。
1. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点。则当PB+PE的值为最小值时,点P的位置在( )21世纪教育网版权所有
A. AC的三等分点 B. AC的中点
C. 连接DE与AC的交点 D. 以上答案都不对
解:如图,连接DE,交AC于P,连接BP,则此时PB+PE的值最小。
∵四边形ABCD是正方形,
∴B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE=DE.
根据两点之间线段最短,所以此时PB+PE的值最小。
故P点即为所求;
故选C.
2.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家。他要完成这件事情所走的最短路程是( )
A. 15 km B. 16 km C. 17 km D. 18 km
解:如图,作出A点关于小河MN的对称点A′,连接A′B交MN于点P,
则A′B就是牧童要完成这件事情所走的最短路程。
在Rt△A′DB中,由勾股定理求得
则他要完成这件事情所走的最短路程是17km.
故选C.
3.如图,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值为______.21·cn·jy·com
解:连接BD,DE,
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,
∴DE的长即为BQ+QE的最小值,
∴△BEQ周长的最小值=DE+BE=5+1=6.
故答案为:6.
4.如图,抛物线y=?x2+bx+c与x轴交于A(1,0),B(?3,0)两点。
(1)求该抛物线的解析式;
(2)设(1)中的_???????????¤yè??_与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;21·世纪*教育网
解:(1)将A(1,0),B(?3,0)代y=?x2+bx+c中得
∴抛物线解析式为:y=?x2?2x+3;
(2)存在
理由如下:由题知A、B两点关于抛物线的对称轴x=?1对称
∴直线BC与x=?1的交点即为Q点,此时△AQC周长最小
∵y=?x2?2x+3
∴C的坐标为:(0,3)
直线BC解析式为:y=x+3(6分)
Q点坐标即为 ∴Q(?1,2)。
第二:利用垂线段最短
(1)点P是∠AOB的内部_??????????????¨O_A上找一点M,在OB上找一点N,使得PN+MN最小.要PN+MN最小,设法将PN,MN转化在同一条直线上,想到作点P关于OB的对称点P′,即求P′N+MN的最小值,因此只要P′M⊥OA,利用垂线段最短即可求解.www-2-1-cnjy-com
(2)“胡不归”问题即点P在直线BM上运动的“PA+k·PB(0
分析:本模型的关_é????¨????????????_定“k·PB”的大小,如图②,过点P作PQ⊥BN于点Q,则k·PB=PB·sin∠MBN=PQ,∴求“PA+k·PB”的最小值转化为求“PA+PQ”的最小值问题,即当A、P、Q三点共线时“PA+k·PB”的值最小(如图③),此时AQ⊥BN,利用垂线段最短求解即可.
特殊情况:当求PA+PB的最小值时,题干中∠MBN的度数一般为30°;当求PA+PB的最小值时,题干中∠MBN的度数一般为45°;当求PA+PB的最小值时,题干中∠MBN的度数一般为60°.【来源:21cnj*y.co*m】
5.如图,在锐角△ABC中,BC=4,∠ABC=45°,BD平分∠ABC,M,N分别是BD、BC上的动点,则CM+MN的最小值是________.【出处:21教育名师】
6.如图,菱形ABCD的边长为3,∠ABC=60°,P是对角线BD上的一个动点,则BP+PC的最小值是( )21教育名师原创作品
7.如图,在Rt△ABC中,∠BAC=90°,且AB=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为________.
解:如解图,连接AD,∵∠_BAC???90_°,DM⊥AB,DN⊥AC,∴四边形AMDN是矩形,∴MN=AD,∴当线段AD最短时,MN最短,即当AD为BC边上的高时,AD最短,在Rt△ABC中,BC==5,S△ABC=×AB·AC=×BC·AD,∴×3×4=×5·AD,∴AD=.∴线段MN的最小值为.
8.如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD+BD的最小值是________.
解:如解图,过点D作DF⊥_AB??????F???_过点C作CQ⊥AB于点Q,易证△BDF∽△BAE,则∠BDF=∠A,∴tan∠BDF=tanA=2.∴=2.设DF=x,则BF=2x,在Rt△BDF中,BD==x,∴cos∠BDF=.∴DF=BD·cos∠BDF=BD.∴CD+BD=CD+DF.∴CD+BD的最小值即为点C到AB的垂线段CQ的长度, 在Rt△AEB中,tanA=2,AB=10,∴BE=4,又∵AB=AC,∴△ACQ≌△ABE.∴CQ=BE=4.
第三:利用三角形成立的条件求最值
(1)同侧差最大值问题
如图,两定点A、B位于直线l同侧,在直线l上找一点P,使得|PA-PB|的值最大
方法:根据三角形任意两边之差_?°??????????è?????_|PA-PB|<AB,则|PA-PB|的最大值为线段AB的长.连接AB并延长,与直线l的交点即为点Pwww.21-cn-jy.com
(2)异侧差最大值问题
如图,两定点A、B位于直线l异侧,在直线l上找一点P,使得|PA-PB|的值最大
方法:将异侧点转化为同侧,同③即可解决.作点B关于直线l的对称点B′,连接AB′并延长,与直线l的交点即为点P
9.如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为________
解析:因为AB为定长,所以取其中_???E??????OE_为定值,在△ODE中,DE为定值,OE为定值,根据三角形三边关系即可得到OD的最大值。即:O,D,E在一直线上OD最大
10..如图,在正方形ABCD中,AB=8,AC与BD交于点O,N是AO的中点,点M在BC边上,且BM=6,P为对角线BD上一点,则PM-PN的最大值为________.
解:如解图,∵四边形AB_CD????????????_,∴AB和CB关于对角线BD对称,作点M关于BD对称的点M′,则点M′在AB上,连接PM′、M′N,根据对称可得BM′=BM=6,又∵AB=8,∴AC=8,AM′=2,AN=AO=×AC=2,∵cos∠M′AN=cos45°==,∴∠AM′N=90°,∴M′N=AM′=2,∵PM-PN=PM′-PN≤M′N=2,∴当点P运动到P′时,即点M′、N、P′共线时,PM-PN=PM′-PN=M′N=2,∴PM-PN的最大值为2.【来源:21·世纪·教育·网】
11.如图,在Rt△ABC中,∠ACB=90°,将△ABC绕顶点C顺时针旋转得到△A′B′C,D是A′B′的中点,连接BD,若BC=2,∠ABC=60°,则线段BD的最大值为________
解:如解图,连接CD,在R_t???ABC???_,∵∠ACB=90°,BC=2,∠ABC=60°,∴∠A=30°,∴A′B′=AB=2BC=4,∵DB′=DA′,∴CD=A′B′=2,∴BD≤CD+CB=4,∴BD的最大值为4.
第四:利用圆求最值
12.如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=6,点D是AB上一动点,将△BCD沿CD所在直线折叠,使点B落在点P处,连接AP,则线段AP的最小值为 ( C )
21*cnjy*com
A. B.3
C.3-3 D.3+3
13.如图,在Rt△ABC中,∠ABC=90°,∠C=30°,AB=1,D为线段AC上一动点(不与点A,C重合),将△BDC沿着BD翻折,点C的对应点为F,E为AC的中点.当EF最短时,EF的长为________
答案:-1
14.如图,正方形ABCD的边长为6,点E,F分别从点D,C同时出发,沿着射线DA,射线CD匀速运动(二者速度相等).设直线AF与直线BE交于点H,连接DH,则线段DH的长度的最小值为________
答案:3-3
15.如图,在边长为2的等边三角形ABC中,点D,E分别是边AC,BC上的动点,且BE=CD,连接AE,BD交于点P,则△ABP的面积的最大值为________
2·1·c·n·j·y
答案:
16.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为________
答案:+
利用函数求最值
17.如图,正方形ABCD的边长是1,点M,N分别在BC,CD上,使得△CMN的周长为2,则△MAN的面积最小值为 。【版权所有:21教育】
:21世纪教育网]
解:延长CB至L,使BL=DN,
则Rt△ABL≌Rt△ADN,故AL=AN,
∵CM+CN+MN=2,CN+DN+CM+BM=1+1=2,
∴MN=DN+BM=BL+BM=ML,∴△AMN≌△AML(SSS),
设CM=x,CN=y,MN=z,x2+y2=z2,
∵x+y+z=2,则x=2-y-z,
∴(2-y-z)2+y2=z2,
整理得2y2+(2z-4)y+(4-4z)=0,
即:y2+(z-2)y+(2-2z)=0
∴△=(z-2)2-4(2-2z)≥0,
∴z2+4z-4≥0
又∵z>0,∴z>2-2
又∵z>0,∴z>2-2
∵S△AMN=S△AML=ML?AB=z。
∴当z=2-2时,S△AMN取得最小值,为-1,故答案为:-1。
18.课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm。要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上。问加工成的正方形零件的边长是多少毫米?21*cnjy*com
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题。
(1)如果原题中要加工的零件_??????????????????_且此矩形是由两个并排放置的正方形所组成,如图1所示,此时,这个矩形零件的两条边长又分别为多少毫米?请你计算。
(2)如果原题中所要加_?·????é???????????_一个矩形,如图2所示,这样,此矩形零件的两条边长就不能确定,但这个矩形的面积有最大值,求达到这个最大值时矩形零件的两条边长。
解:(1)设矩形的边长PN=2y(mm),则PQ=y(mm),由条件可得△APN∽△ABC,
∴=,即=,解得y=,
∴PN=×2=(mm)。
答:这个矩形零件的两条边长分别为mm,mm。
(2)设PN=x(mm),由条件可得△APN∽△ABC,21世纪教育网
∴=,即=,
解得PQ=80-x,
∴S=PN?PQ=x(80-x)=-x2+80x=-(x-60)2+2400,
∴S的最大值为2400mm2,此时PN=60mm,PQ=80-×60=40(mm)
19. 如图,P是抛物线y=-x2+x+2在第一象限上的点,过点P分别向x轴和y轴引垂线,垂足分别为A,B,则四边形OAPB周长的最大值为 。21教育网
解析:设一条边为自变量x,周长为因变量y,建立函数关系式即可
20.如图,正方形ABCD的边长为4,E、F分别是BC、CD上的两个动点,且AE⊥EF。则AF的最小值是 。21cnjy.com
解析:通过数量关系和位置关系,建立函数关系式即可
_21?????????è?????(www.21cnjy.com)_
同课章节目录
