气体的等温变化
图片预览





文档简介
(共18张PPT)
第八章 气 体
1.气体的等温变化
一.引入:思考题
1.被封气体V如何变化
2.是不是压强变大体积一定变小
不一定如果T升高,P变大,V也可能大
不一定,如果给自行车轮胎充气,P增大,气体并没有变小.
3.怎么样研究P.T.V三者关系
控制变量法
二、等温变化
1.气体的等温变化:一定质量的气体温度保持不变的状态变化过程.
2.研究一定质量的气体等温变化的规律
(1)介绍实验装置
(2)观察实验装置,并回答:
①研究哪部分气体?
②怎样保证M不变
③A管中气体体积怎样表示?
(L·S)
④阀门a打开时,A管中气体压强多大?阀门a闭合时A管中气体压强多大?
(p0)
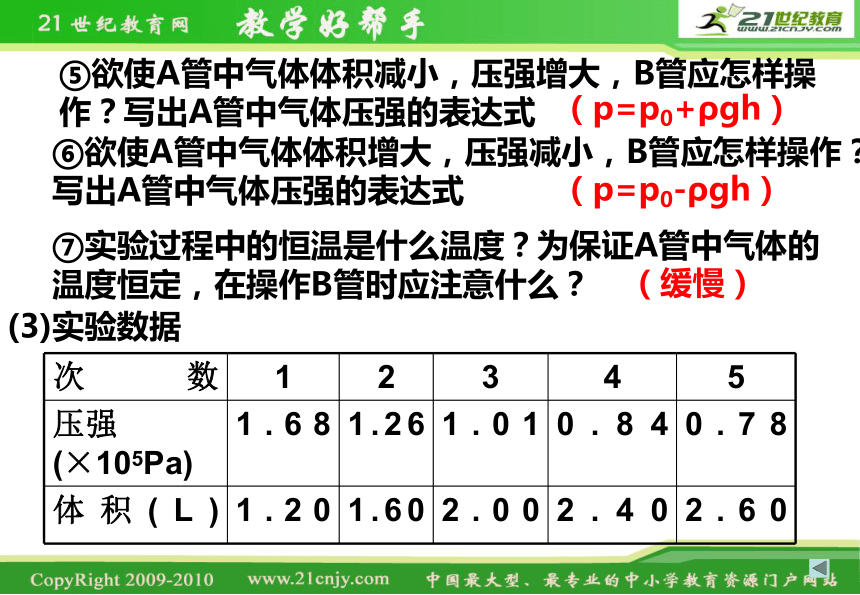
⑤欲使A管中气体体积减小,压强增大,B管应怎样操作?写出A管中气体压强的表达式
(p=p0+ρgh)
⑥欲使A管中气体体积增大,压强减小,B管应怎样操作?写出A管中气体压强的表达式
(p=p0-ρgh)
⑦实验过程中的恒温是什么温度?为保证A管中气体的温度恒定,在操作B管时应注意什么?
(缓慢)
(3)实验数据
次数 1 2 3 4 5
压强(×105Pa) 1.68 1.26 1.01
0.84 0.78
体积(L) 1.20 1.60 2.00 2.40 2.60
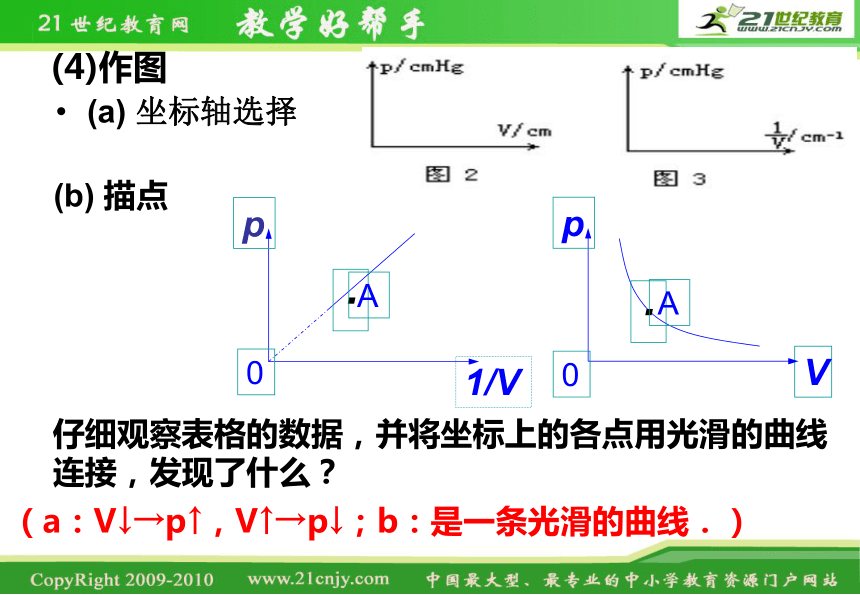
(4)作图
(a) 坐标轴选择
p
1/V
·
0
V
p
·
0
A
A
(b) 描点
仔细观察表格的数据,并将坐标上的各点用光滑的曲线连接,发现了什么?
(a:V↓→p↑,V↑→p↓;b:是一条光滑的曲线.)
等温变化图象的特点:
(1)等温线是双曲线的一支。
(2)温度越高,其等温线离原点越远.
思考与讨论
同一气体,不同温度下等温线是不同的,你能判断那条等温线是表示温度较高的情形吗?你是根据什么理由作出判断的?
V
p
1
2
3
0
结论:t3>t2>t1
恒量随温度升高而增大(与气体的质量种类温度有关)。
(5)图象意义
(1)物理意义:反映压强随体积的变化关系
(2)点意义:每一组数据---反映某一状态
(3)结论:体积缩小到原来的几分之一,压强增大到原来的几倍.体积增大到原来的几倍,它的压强就减小为原来的几分之一.
三 、实验结论---玻意耳定律
1、文字表述:一定质量某种气体,在温度不变
的情况下,压强p与体积V成反比。
2、公式表述:pV=常数 或p1V1=p2V2
3、条件:一定质量气体且温度不变
4、适用范围:温度不太低,压强不太大
例1. 将一端封闭的均匀直玻璃管开口向下,竖直插入水银中,当管顶距槽中水银面8 cm时,管内水银面比管外水银面低2 cm.要使管内水银面比管外水银面高2 cm,应将玻璃管竖直向上提起多少厘米?已知大气压强p0支持76 cmHg,设温度不变.
分析:均匀直玻璃管、U形玻璃管、汽缸活塞中封闭气体的等温过程是三种基本物理模型,所以在复习中必须到位.在确定初始条件时,无
论是压强还是体积的计算,都离不
开几何关系的分析,那么,画好始
末状态的图形,对解题便会有很大
作用.本题主要目的就是怎样去画
始末状态的图形以找到几何关系,
来确定状态参量.
解:根据题意,由图知
p1=p0+2cmHg=78cmHg,V1=(8+2)S=10S,
p2=p0-2cmHg=74cmHg,
V2=[(8+x)-2]·S=(6+x)S.
用气体定律解题的步骤
1.确定研究对象.被封闭的气体(满足质量不变的条
件);
2.用一定的数字或表达式写出气体状态的初始条件
(p1,V1,T1,p2,V2,T2);
3.根据气体状态变化过程的特点,列出相应的气体公
式(本节课中就是玻意耳定律公式);
4.将各初始条件代入气体公式中,求解未知量;
5.对结果的物理意义进行讨论.
练习1.一根一端封闭的玻璃管开口向下插入水银槽中,内封一定质量的气体,管内水银面低于管外,在温度不变时,将玻璃管稍向下插入一些,下列说法正确的是,如图所示. ( )
A.玻璃管内气体体积减小;
B.玻璃管内气体体积增大;
C.管内外水银面高度差减小;
D.管内外水银面高度差增大.
AD
练习2.如图所示,注有水银的U型管,A管上端封闭,A、B两管用橡皮管相通.开始时两管液面相平,现将B管缓慢降低,在这一过程中,A管内气体体积____,B管比A管液面____.
强调思路,由V的变化→压强变化→借助p的计算判断液面的高低.
例2. 均匀U形玻璃管竖直放置,用水银将一些空气封在A管内,当A、B两管水银面相平时,大气压强支持72 cmHg.A管内空气柱长度为10 cm,现往B管中注入水银,当两管水银面高度差为18 cm时,A管中空气柱长度是多少?注入水银柱长度是多少?
解: p1=p0=72 cm Hg,V1=10S,
分析:如图所示,由于水银是不可压缩的,所以A管水银面上升高度x时,B管原水银面
下降同样高度x.那么,当A、B
两管水银面高度差为18 cm时,
在B管中需注入的水银柱长度应
为(18+2x)cm.
V2=lS
p2=p0+18=90 cmHg
例3. 密闭圆筒内有一质量为100 g的活塞,活塞与圆筒顶端之间有一根劲度系数k=20 N/m的轻弹簧;圆筒放在水平地面上,活塞将圆筒分成两部分,A室为真空,B室充有空气,平衡时,l0=0.10 m,弹簧刚好没有形变如图5所示.现将圆筒倒置,问这时B室的高度是多少?
分析:汽缸类问题,求压强是关键:应根据共点力平衡条件或牛顿第二定律计算压强.
解:圆筒正立时:
圆筒倒立时,受力分析如图所示,有p2S+mg=kx,
x=l-l0,则
温度不变,根据玻意耳定律:p1V1=p2V2.
例4. 某个容器的容积是10 L,所装气体的压强是20×105 Pa。如果温度保持不变,把容器的开关打开以后,容器里剩下的气体是原来的百分之几?设大气压是1.0×105 Pa。
解: 设容器原装气体为研究对象。
初态 p1=20×105Pa V1=10L T1=T
末态 p2=1.0×105Pa V2=?L T2=T
由玻意耳定律 p1V1=p2V2得
即剩下的气体为原来的5%。
就容器而言,里面气体质量变了,似乎是变质量问题了,但若视容器中气体出而不走,就又是质量不变了。
第八章 气 体
1.气体的等温变化
一.引入:思考题
1.被封气体V如何变化
2.是不是压强变大体积一定变小
不一定如果T升高,P变大,V也可能大
不一定,如果给自行车轮胎充气,P增大,气体并没有变小.
3.怎么样研究P.T.V三者关系
控制变量法
二、等温变化
1.气体的等温变化:一定质量的气体温度保持不变的状态变化过程.
2.研究一定质量的气体等温变化的规律
(1)介绍实验装置
(2)观察实验装置,并回答:
①研究哪部分气体?
②怎样保证M不变
③A管中气体体积怎样表示?
(L·S)
④阀门a打开时,A管中气体压强多大?阀门a闭合时A管中气体压强多大?
(p0)
⑤欲使A管中气体体积减小,压强增大,B管应怎样操作?写出A管中气体压强的表达式
(p=p0+ρgh)
⑥欲使A管中气体体积增大,压强减小,B管应怎样操作?写出A管中气体压强的表达式
(p=p0-ρgh)
⑦实验过程中的恒温是什么温度?为保证A管中气体的温度恒定,在操作B管时应注意什么?
(缓慢)
(3)实验数据
次数 1 2 3 4 5
压强(×105Pa) 1.68 1.26 1.01
0.84 0.78
体积(L) 1.20 1.60 2.00 2.40 2.60
(4)作图
(a) 坐标轴选择
p
1/V
·
0
V
p
·
0
A
A
(b) 描点
仔细观察表格的数据,并将坐标上的各点用光滑的曲线连接,发现了什么?
(a:V↓→p↑,V↑→p↓;b:是一条光滑的曲线.)
等温变化图象的特点:
(1)等温线是双曲线的一支。
(2)温度越高,其等温线离原点越远.
思考与讨论
同一气体,不同温度下等温线是不同的,你能判断那条等温线是表示温度较高的情形吗?你是根据什么理由作出判断的?
V
p
1
2
3
0
结论:t3>t2>t1
恒量随温度升高而增大(与气体的质量种类温度有关)。
(5)图象意义
(1)物理意义:反映压强随体积的变化关系
(2)点意义:每一组数据---反映某一状态
(3)结论:体积缩小到原来的几分之一,压强增大到原来的几倍.体积增大到原来的几倍,它的压强就减小为原来的几分之一.
三 、实验结论---玻意耳定律
1、文字表述:一定质量某种气体,在温度不变
的情况下,压强p与体积V成反比。
2、公式表述:pV=常数 或p1V1=p2V2
3、条件:一定质量气体且温度不变
4、适用范围:温度不太低,压强不太大
例1. 将一端封闭的均匀直玻璃管开口向下,竖直插入水银中,当管顶距槽中水银面8 cm时,管内水银面比管外水银面低2 cm.要使管内水银面比管外水银面高2 cm,应将玻璃管竖直向上提起多少厘米?已知大气压强p0支持76 cmHg,设温度不变.
分析:均匀直玻璃管、U形玻璃管、汽缸活塞中封闭气体的等温过程是三种基本物理模型,所以在复习中必须到位.在确定初始条件时,无
论是压强还是体积的计算,都离不
开几何关系的分析,那么,画好始
末状态的图形,对解题便会有很大
作用.本题主要目的就是怎样去画
始末状态的图形以找到几何关系,
来确定状态参量.
解:根据题意,由图知
p1=p0+2cmHg=78cmHg,V1=(8+2)S=10S,
p2=p0-2cmHg=74cmHg,
V2=[(8+x)-2]·S=(6+x)S.
用气体定律解题的步骤
1.确定研究对象.被封闭的气体(满足质量不变的条
件);
2.用一定的数字或表达式写出气体状态的初始条件
(p1,V1,T1,p2,V2,T2);
3.根据气体状态变化过程的特点,列出相应的气体公
式(本节课中就是玻意耳定律公式);
4.将各初始条件代入气体公式中,求解未知量;
5.对结果的物理意义进行讨论.
练习1.一根一端封闭的玻璃管开口向下插入水银槽中,内封一定质量的气体,管内水银面低于管外,在温度不变时,将玻璃管稍向下插入一些,下列说法正确的是,如图所示. ( )
A.玻璃管内气体体积减小;
B.玻璃管内气体体积增大;
C.管内外水银面高度差减小;
D.管内外水银面高度差增大.
AD
练习2.如图所示,注有水银的U型管,A管上端封闭,A、B两管用橡皮管相通.开始时两管液面相平,现将B管缓慢降低,在这一过程中,A管内气体体积____,B管比A管液面____.
强调思路,由V的变化→压强变化→借助p的计算判断液面的高低.
例2. 均匀U形玻璃管竖直放置,用水银将一些空气封在A管内,当A、B两管水银面相平时,大气压强支持72 cmHg.A管内空气柱长度为10 cm,现往B管中注入水银,当两管水银面高度差为18 cm时,A管中空气柱长度是多少?注入水银柱长度是多少?
解: p1=p0=72 cm Hg,V1=10S,
分析:如图所示,由于水银是不可压缩的,所以A管水银面上升高度x时,B管原水银面
下降同样高度x.那么,当A、B
两管水银面高度差为18 cm时,
在B管中需注入的水银柱长度应
为(18+2x)cm.
V2=lS
p2=p0+18=90 cmHg
例3. 密闭圆筒内有一质量为100 g的活塞,活塞与圆筒顶端之间有一根劲度系数k=20 N/m的轻弹簧;圆筒放在水平地面上,活塞将圆筒分成两部分,A室为真空,B室充有空气,平衡时,l0=0.10 m,弹簧刚好没有形变如图5所示.现将圆筒倒置,问这时B室的高度是多少?
分析:汽缸类问题,求压强是关键:应根据共点力平衡条件或牛顿第二定律计算压强.
解:圆筒正立时:
圆筒倒立时,受力分析如图所示,有p2S+mg=kx,
x=l-l0,则
温度不变,根据玻意耳定律:p1V1=p2V2.
例4. 某个容器的容积是10 L,所装气体的压强是20×105 Pa。如果温度保持不变,把容器的开关打开以后,容器里剩下的气体是原来的百分之几?设大气压是1.0×105 Pa。
解: 设容器原装气体为研究对象。
初态 p1=20×105Pa V1=10L T1=T
末态 p2=1.0×105Pa V2=?L T2=T
由玻意耳定律 p1V1=p2V2得
即剩下的气体为原来的5%。
就容器而言,里面气体质量变了,似乎是变质量问题了,但若视容器中气体出而不走,就又是质量不变了。
