磁场对运动电荷的作用
图片预览




文档简介
(共17张PPT)
第四节
磁场对运动电荷的作用
电量为 q 电荷在磁场中受到的洛仑兹力:
大小:
1.洛仑兹力
一、磁场对运动电荷的作用—洛仑兹力
方向:
垂直由 和 构成的平面。
洛仑兹力不对运动电荷作功,它只改变带电粒子的运动方向,并不改变带电粒子的速率和动能。
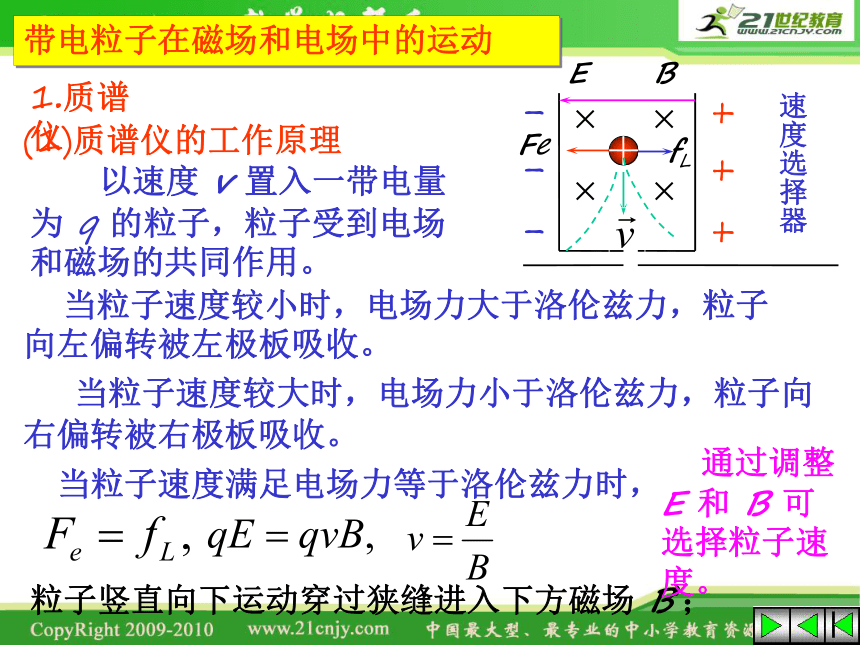
以速度 v 置入一带电量为 q 的粒子,粒子受到电场和磁场的共同作用。
+
+
+
-
-
-
E
速度选择器
Fe
fL
B
当粒子速度较小时,电场力大于洛伦兹力,粒子向左偏转被左极板吸收。
带电粒子在磁场和电场中的运动
(1)质谱仪的工作原理
1.质谱仪
当粒子速度较大时,电场力小于洛伦兹力,粒子向右偏转被右极板吸收。
当粒子速度满足电场力等于洛伦兹力时,
粒子竖直向下运动穿过狭缝进入下方磁场 B’;
通过调整 E 和 B 可选择粒子速度。
R
B’
+
+
+
-
-
-
v
E
速度选择器
Fe
fL
B
质量大的同位素粒子,轨道半径大,质量小的同位素粒子,轨道半径小。不同质量的粒子在胶片屏上留下不同的质谱线。
在 B’ 中作圆周运动的轨道半径为:
根据质谱线的位置,可推出同位素的质量。
(2)同位素
有相同的质子数和电子数,但中子数不同的元素。它们的化学性质相同,无法用化学的方向将它们分离开。
由 知:
质谱线:
其结构为金属双 D 形盒,在其上加有磁场和交变的电场。
2.回旋加速器
由于金属具有静电屏蔽作用,带电粒子在磁场的作用下作圆周运动,进入缝隙后,电场极性变换,粒子被反向加速,进入右半盒,由于速度增加,轨道半径也增加。然后又穿过缝隙,电场极性又变换,粒子不断地被加速。
将一粒子置于双 D形盒的缝隙处,在电场的作用下,进入左半盒。
~
B
B
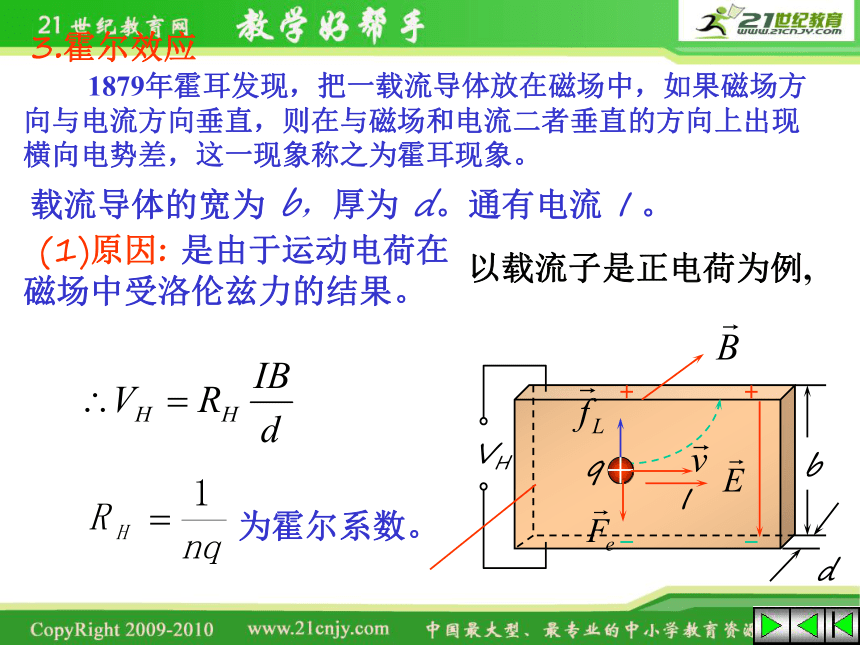
(1)原因: 是由于运动电荷在磁场中受洛伦兹力的结果。
载流导体的宽为 b,厚为 d。通有电流 I 。
1879年霍耳发现,把一载流导体放在磁场中,如果磁场方向与电流方向垂直,则在与磁场和电流二者垂直的方向上出现横向电势差,这一现象称之为霍耳现象。
I
b
d
VH
q
3.霍尔效应
以载流子是正电荷为例,
为霍尔系数。
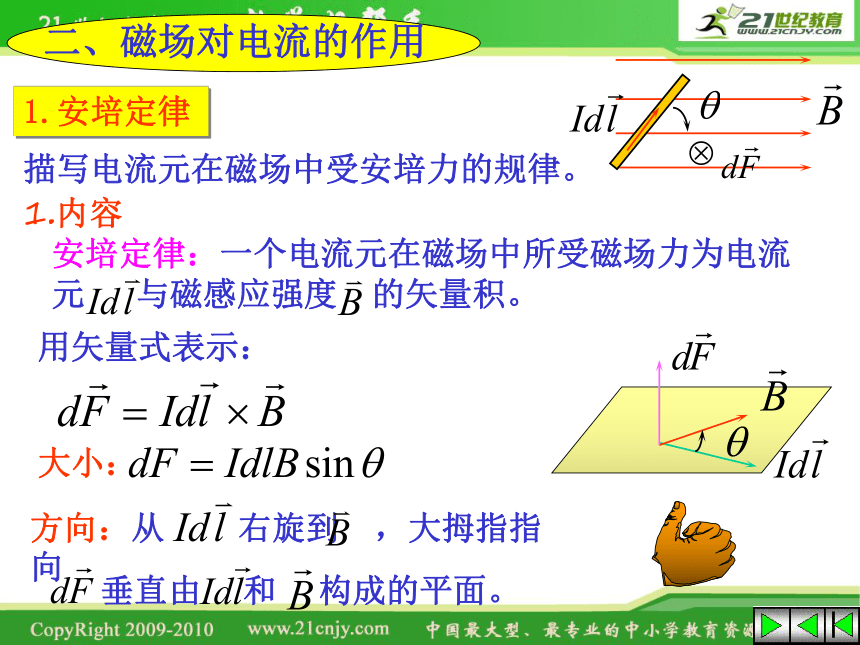
描写电流元在磁场中受安培力的规律。
大小:
用矢量式表示:
二、磁场对电流的作用
1.安培定律
1.内容
安培定律:一个电流元在磁场中所受磁场力为电流元 与磁感应强度 的矢量积。
方向:从 右旋到 ,大拇指指向
垂直由 和 构成的平面。
计算一段电流在磁场中受到的安培力时,应先将其分割成无限多电流元,将所有电流元受到的安培力矢量求和----矢量积分。
均匀磁场中曲线电流受的安培力,等于从起点到终点的直线电流所受的安培力。
由于 ,
a
b
I
2.一段电流在磁场中受力
3.均匀磁场中曲线电流受力
例1:在无限长载流直导线 I1 旁,平行放置另一长为L的载流直导线 I2 ,两根导线相距为 a,求导线 I2所受到的安培力。
解:由于电流 I2 上各点到电流 I1 距离相同,I2 各点处的 B 相同,
I2 受到的安培力方向如图所示,
其中
I2 受到 I1 的引力。
同理 I1 也受到 I2 的引力。
安培力大小:
例2:在无限长载流直导线 I1 旁,垂直放置另一长为 L 的载流直导线 I2 , I2 导线左端距 I1 为 a,求导线 I2 所受到的安培力。
解:
建立坐标系,坐标原点选在 I1上,
电流元受安培力大小为:
其中
分割电流元, 长度为 dx ,
例3:在均匀磁场中,放置一半圆形半径为 R 通有电流为 I 的载流导线,求载流导线所受的安培力。
解:由均匀磁场中曲线电流受力的结论:半圆形电流受到的安培力相当于沿直径电流受到的安培;
R
⊙
将平面载流线圈放入均匀磁场中,
电磁系列电表指针转动:在永久磁铁的两极之间的空气隙内放一个可绕固定轴转动的线圈,载流线圈在磁场中受力矩的结果。
2.磁场对载流线圈的作用
1.载流线圈在磁场中受到的力矩
规定:与电流满足右手定则的法线方向为正向。
da边受到安培力:
bc边受到安培力:
Fda 与 Fbc大小相等方向相反,作用在一条直线上,相互抵消。
ab边受到安培力:
cd边受到安培力:
Fab与Fcd大小相等方向相反,不在一条直线上,不能抵消,为一对力偶,产生力矩。
作俯视图,
线圈受到的力矩大小为:
如果为N匝平面线圈:
S 闭合电流所包围的面积!
大小:
单位:安培·米2
方向:线圈正法线方向;
定义:磁矩
法线方向的单位矢量。
考虑方向:
力矩方向为:四指从 右旋到 ,大拇指指向。
上述结论具有普遍意义(也适用于带电粒子沿任意闭合回路的运动或自旋磁矩在磁场中受的力矩) 。
1. = 0 时,
线圈处于稳定平衡态。这时如果外界的扰动使线圈稍有偏离,磁场的力矩会使它回到平衡位置。
2. = 90 时:
线圈受力矩最大。
3. = 180 时:
线圈处于非稳定平衡态。这时如果外界的扰动使线圈稍有偏离,磁场的力矩会使它继续偏转。
线圈受力矩为0。
2.讨论
线圈受力矩为0。
例1:一半径为 R 的薄圆盘,放在磁感应强度为 B 的均匀磁场中, B 的方向与盘面平行,如图所示,圆盘表面的电荷面密度为 s ,若圆盘以角速度 w 绕其轴线转动,试求作用在圆盘上的磁力矩。
解:取半径为 r, 宽为dr的圆环。
圆环带电量:
转动形成电流
磁矩:
方向沿轴线向上,
所受磁力矩:
方向为
顺时钟方向为为规定的坐标正方向
1 .载流导线在磁场中运动时磁力的功
2 .载流线圈在磁场中转动时磁力矩的功
3.磁力的功
第四节
磁场对运动电荷的作用
电量为 q 电荷在磁场中受到的洛仑兹力:
大小:
1.洛仑兹力
一、磁场对运动电荷的作用—洛仑兹力
方向:
垂直由 和 构成的平面。
洛仑兹力不对运动电荷作功,它只改变带电粒子的运动方向,并不改变带电粒子的速率和动能。
以速度 v 置入一带电量为 q 的粒子,粒子受到电场和磁场的共同作用。
+
+
+
-
-
-
E
速度选择器
Fe
fL
B
当粒子速度较小时,电场力大于洛伦兹力,粒子向左偏转被左极板吸收。
带电粒子在磁场和电场中的运动
(1)质谱仪的工作原理
1.质谱仪
当粒子速度较大时,电场力小于洛伦兹力,粒子向右偏转被右极板吸收。
当粒子速度满足电场力等于洛伦兹力时,
粒子竖直向下运动穿过狭缝进入下方磁场 B’;
通过调整 E 和 B 可选择粒子速度。
R
B’
+
+
+
-
-
-
v
E
速度选择器
Fe
fL
B
质量大的同位素粒子,轨道半径大,质量小的同位素粒子,轨道半径小。不同质量的粒子在胶片屏上留下不同的质谱线。
在 B’ 中作圆周运动的轨道半径为:
根据质谱线的位置,可推出同位素的质量。
(2)同位素
有相同的质子数和电子数,但中子数不同的元素。它们的化学性质相同,无法用化学的方向将它们分离开。
由 知:
质谱线:
其结构为金属双 D 形盒,在其上加有磁场和交变的电场。
2.回旋加速器
由于金属具有静电屏蔽作用,带电粒子在磁场的作用下作圆周运动,进入缝隙后,电场极性变换,粒子被反向加速,进入右半盒,由于速度增加,轨道半径也增加。然后又穿过缝隙,电场极性又变换,粒子不断地被加速。
将一粒子置于双 D形盒的缝隙处,在电场的作用下,进入左半盒。
~
B
B
(1)原因: 是由于运动电荷在磁场中受洛伦兹力的结果。
载流导体的宽为 b,厚为 d。通有电流 I 。
1879年霍耳发现,把一载流导体放在磁场中,如果磁场方向与电流方向垂直,则在与磁场和电流二者垂直的方向上出现横向电势差,这一现象称之为霍耳现象。
I
b
d
VH
q
3.霍尔效应
以载流子是正电荷为例,
为霍尔系数。
描写电流元在磁场中受安培力的规律。
大小:
用矢量式表示:
二、磁场对电流的作用
1.安培定律
1.内容
安培定律:一个电流元在磁场中所受磁场力为电流元 与磁感应强度 的矢量积。
方向:从 右旋到 ,大拇指指向
垂直由 和 构成的平面。
计算一段电流在磁场中受到的安培力时,应先将其分割成无限多电流元,将所有电流元受到的安培力矢量求和----矢量积分。
均匀磁场中曲线电流受的安培力,等于从起点到终点的直线电流所受的安培力。
由于 ,
a
b
I
2.一段电流在磁场中受力
3.均匀磁场中曲线电流受力
例1:在无限长载流直导线 I1 旁,平行放置另一长为L的载流直导线 I2 ,两根导线相距为 a,求导线 I2所受到的安培力。
解:由于电流 I2 上各点到电流 I1 距离相同,I2 各点处的 B 相同,
I2 受到的安培力方向如图所示,
其中
I2 受到 I1 的引力。
同理 I1 也受到 I2 的引力。
安培力大小:
例2:在无限长载流直导线 I1 旁,垂直放置另一长为 L 的载流直导线 I2 , I2 导线左端距 I1 为 a,求导线 I2 所受到的安培力。
解:
建立坐标系,坐标原点选在 I1上,
电流元受安培力大小为:
其中
分割电流元, 长度为 dx ,
例3:在均匀磁场中,放置一半圆形半径为 R 通有电流为 I 的载流导线,求载流导线所受的安培力。
解:由均匀磁场中曲线电流受力的结论:半圆形电流受到的安培力相当于沿直径电流受到的安培;
R
⊙
将平面载流线圈放入均匀磁场中,
电磁系列电表指针转动:在永久磁铁的两极之间的空气隙内放一个可绕固定轴转动的线圈,载流线圈在磁场中受力矩的结果。
2.磁场对载流线圈的作用
1.载流线圈在磁场中受到的力矩
规定:与电流满足右手定则的法线方向为正向。
da边受到安培力:
bc边受到安培力:
Fda 与 Fbc大小相等方向相反,作用在一条直线上,相互抵消。
ab边受到安培力:
cd边受到安培力:
Fab与Fcd大小相等方向相反,不在一条直线上,不能抵消,为一对力偶,产生力矩。
作俯视图,
线圈受到的力矩大小为:
如果为N匝平面线圈:
S 闭合电流所包围的面积!
大小:
单位:安培·米2
方向:线圈正法线方向;
定义:磁矩
法线方向的单位矢量。
考虑方向:
力矩方向为:四指从 右旋到 ,大拇指指向。
上述结论具有普遍意义(也适用于带电粒子沿任意闭合回路的运动或自旋磁矩在磁场中受的力矩) 。
1. = 0 时,
线圈处于稳定平衡态。这时如果外界的扰动使线圈稍有偏离,磁场的力矩会使它回到平衡位置。
2. = 90 时:
线圈受力矩最大。
3. = 180 时:
线圈处于非稳定平衡态。这时如果外界的扰动使线圈稍有偏离,磁场的力矩会使它继续偏转。
线圈受力矩为0。
2.讨论
线圈受力矩为0。
例1:一半径为 R 的薄圆盘,放在磁感应强度为 B 的均匀磁场中, B 的方向与盘面平行,如图所示,圆盘表面的电荷面密度为 s ,若圆盘以角速度 w 绕其轴线转动,试求作用在圆盘上的磁力矩。
解:取半径为 r, 宽为dr的圆环。
圆环带电量:
转动形成电流
磁矩:
方向沿轴线向上,
所受磁力矩:
方向为
顺时钟方向为为规定的坐标正方向
1 .载流导线在磁场中运动时磁力的功
2 .载流线圈在磁场中转动时磁力矩的功
3.磁力的功
