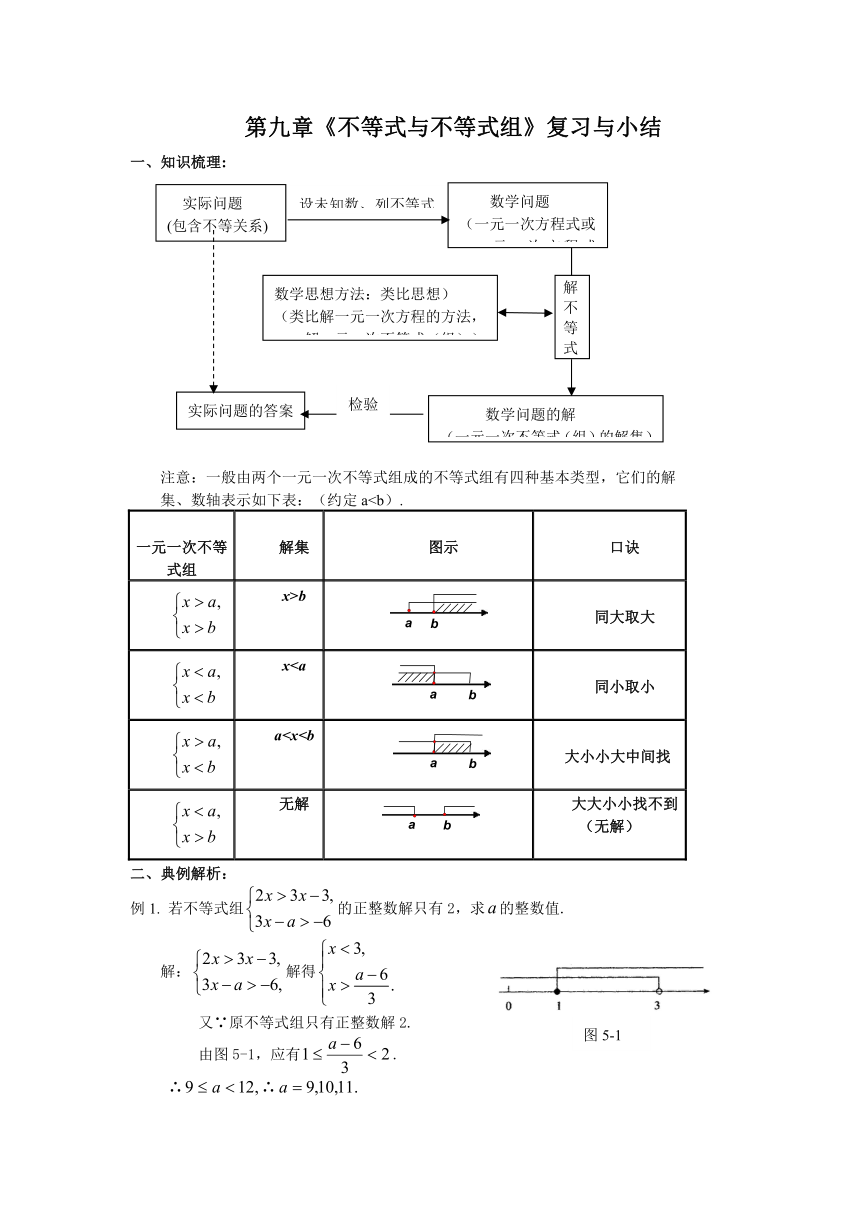
第九章《不等式与不等式组》复习与小结
文档属性
| 名称 | 第九章《不等式与不等式组》复习与小结 |
|
|
| 格式 | zip | ||
| 文件大小 | 45.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-17 00:00:00 | ||
图片预览


