2021-2022学年人教五四新版六年级上册数学《第3章 圆的初步认识》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年人教五四新版六年级上册数学《第3章 圆的初步认识》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 260.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教五四新版六年级上册数学《第3章
圆的初步认识》单元测试卷
一.选择题
1.一个扇形的圆心角为120°,半径为3,则这个扇形的面积是( )
A.π
B.2π
C.3π
D.4π
2.下列说法中,正确的是( )
A.弦是直径
B.半圆是弧
C.过圆心的线段是直径
D.圆心相同半径相同的两个圆是同心圆
3.下列说法错误的是( )
A.直径是圆中最长的弦
B.长度相等的两条弧是等弧
C.面积相等的两个圆是等圆
D.半径相等的两个半圆是等弧
4.如图,⊙O中,点A,O,D以及点B,O,C分别在一条直线上,图中弦的条数有( )
A.2条
B.3条
C.4条
D.5条
5.到圆心的距离不大于半径的点的集合是( )
A.圆的外部
B.圆的内部
C.圆
D.圆的内部和圆
6.如图所示,MN为⊙O的弦,∠N=50°,则∠MON的度数为( )
A.40°
B.50°
C.80°
D.100°
7.如图,AB是半圆的直径,AB=2r,C、D为半圆的三等分点,则图中阴影部分的面积是( )
A.
B.
C.
D.
8.如图,在扇形OAB中,已知∠AOB=90°,OA=,过的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为( )
A.π﹣1
B.﹣1
C.π﹣
D.﹣
二.填空题
9.到点O的距离等于8的点的集合是
.
10.已知⊙O的半径为5cm,则圆中最长的弦长为
cm.
11.已知⊙O中最长的弦为16cm,则⊙O的半径为
cm.
12.已知一个扇形的半径为6cm,圆心角为120°,则这个扇形的面积为
cm2.
13.点A、B在⊙O上,若∠AOB=40°,则∠OAB=
.
14.如图,在扇形OAB中,已知∠AOB=90°,OA=,过弧AB的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为
.
15.如图在以点O为圆心的两个同心圆中,大圆的半径为2,小圆的半径为1,∠AOB=100°.则阴影部分的面积是
.
16.如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是
.
三.解答题
17.一个扇形的圆心角60°,半径为12cm,求它的面积.(保留π)
18.如图,圆心为点M的三个半圆的直径都在x轴上,所有标注A的图形面积都是SA,所有标注B的图形面积都是SB.
(1)求标注C的图形面积SC;
(2)求SA:SB.
19.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长l=πa.
计算:(1)把AB分成两条相等的线段,每个小圆的周长;
(2)把AB分成三条相等的线段,每个小圆的周长l3=
;
(3)把AB分成四条相等的线段,每个小圆的周长l4=
;
(4)把AB分成n条相等的线段,每个小圆的周长ln=
.
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的
.请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
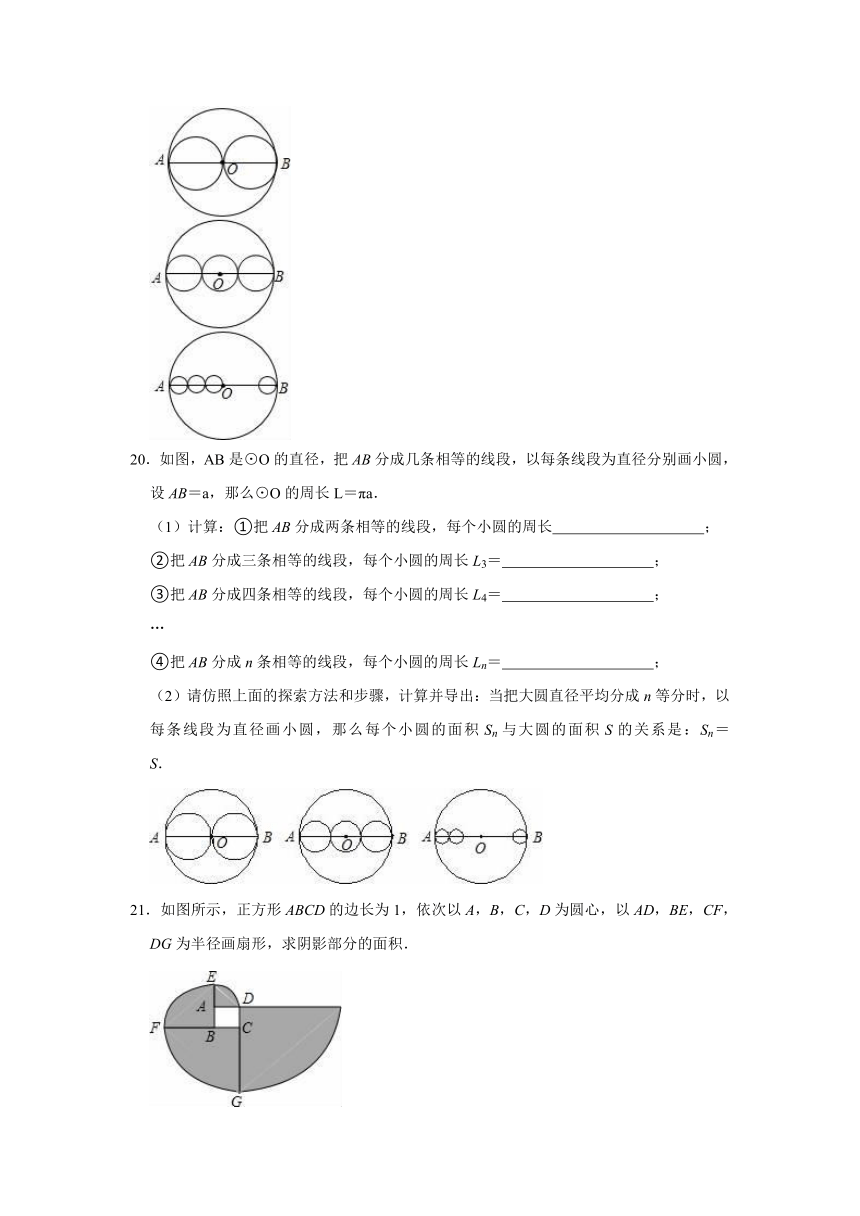
20.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长L=πa.
(1)计算:①把AB分成两条相等的线段,每个小圆的周长
;
②把AB分成三条相等的线段,每个小圆的周长L3=
;
③把AB分成四条相等的线段,每个小圆的周长L4=
;
…
④把AB分成n条相等的线段,每个小圆的周长Ln=
;
(2)请仿照上面的探索方法和步骤,计算并导出:当把大圆直径平均分成n等分时,以每条线段为直径画小圆,那么每个小圆的面积Sn与大圆的面积S的关系是:Sn=
S.
21.如图所示,正方形ABCD的边长为1,依次以A,B,C,D为圆心,以AD,BE,CF,DG为半径画扇形,求阴影部分的面积.
参考答案与试题解析
一.选择题
1.解:这个扇形的面积==3π.
故选:C.
2.解:A、直径是弦,但弦不一定是直径,故错误;
B、半圆是弧,正确;
C、过圆心的弦是直径,故错误;
D、圆心相同半径不同的两个圆是同心圆,故错误,
故选:B.
3.解:A、直径是圆中最长的弦,所以A选项的说法正确;
B、在同圆或等圆中,长度相等的两条弧是等弧,所以B选项的说法错误;
C、面积相等的两个圆的半径相等,则它们是等圆,所以C选项的说法正确;
D、半径相等的两个半圆是等弧,所以D选项的说法正确.
故选:B.
4.解:图中的弦有AB,BC,CE共三条,
故选:B.
5.解:根据点和圆的位置关系,知圆的内部是到圆心的距离小于的所有点的集合;
圆是到圆心的距离等于半径的所有点的集合.
所以与圆心的距离不大于半径的点所组成的图形是圆的内部(包括边界).
故选:D.
6.解:∵OM=ON,
∴∠M=∠N=50°,
∴∠MON=180°﹣2×50°=80°.
故选:C.
7.解:连接OC、OD.
∵△COD和△CDA等底等高,
∴S△COD=S△ACD.
∵点C,D为半圆的三等分点,AB=2r,
∴∠COD=180°÷3=60°,OA=r,
∴阴影部分的面积=S扇形COD==πr2.
故选:B.
8.解:∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=∠AOB=90°,
∴四边形CDOE是矩形,
连接OC,
∵点C是的中点,
∴∠AOC=∠BOC,
∵OC=OC,
∴△COD≌△COE(AAS),
∴OD=OE,
∴矩形CDOE是正方形,
∵OC=OA=,
∴OE=1,
∴图中阴影部分的面积=﹣1×1=﹣1,
故选:B.
二.填空题
9.解:到点O的距离等于8的点的集合是:以点O为圆心,以8为半径的圆.
故答案是:以点O为圆心,以8为半径的圆.
10.解:∵⊙O的半径为5cm,
∴⊙O的直径为10cm,
即圆中最长的弦长为10cm.
故答案为10.
11.解:∵⊙O中最长的弦为16cm,即直径为16cm,
∴⊙O的半径为8cm.
故答案为:8.
12.解:∵r=6cm,n=120°,
根据扇形的面积公式S=得
S扇==12(cm2).
故答案为:12π.
13.解:如图,
∵∠AOB=40°,OA=OB,
∴∠OAB=∠OBA==70°,
故答案为:70°.
14.解:∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=∠AOB=90°,
∴四边形CDOE是矩形,
连接OC,
∵点C是弧AB的中点,
∴∠AOC=∠BOC,
∵OC=OC,
∴△COD≌△COE(AAS),
∴OD=OE,
∴矩形CDOE是正方形,
∵OC=OA=,
∴OE=1,
∴图中阴影部分的面积=﹣1×1=﹣1,
故答案为﹣1.
15.解:S阴影=﹣=π,
故答案为π.
16.解:由AB=OC,得
AB=OB,
∠A=∠AOB.
由BO=EO,得
∠BEO=∠EBO.
由∠EBO是△ABO的外角,得
∠EBO=∠A+∠AOB=2∠A,
∠BEO=∠EBO=2∠A.
由∠DOE是△AOE的外角,得
∠A+∠AEO=∠EOD,
即∠A+2∠A=84°,
∠A=28°.
故答案为:28°.
三.解答题
17.解:由扇形面积公式得:S==24π(cm2),
故扇形的面积为:24πcm2.
18.解:(1)由题意得到圆M的半径为(6﹣4)÷2=1,
则.(1分)
(2)
∴(3分)
∵
∴(5分)
∴
即SA:SB=5:6(6分)
19.解:(2)l;
(3)l;
(4)l;;
每个小圆面积=π(?a)2=?,而大圆的面积=π(?a)2=πa2
即每个小圆的面积是大圆的面积的.
20.解:(1)根据L=πd,
①把AB分成两条相等的线段,每个小圆的周长L2=a=L;
②把AB分成三条相等的线段,每个小圆的周长L3=a=L,
③把AB分成四条相等的线段,每个小圆的周长L4=a=L;
④把AB分成n条相等的线段,每个小圆的周长Ln=a=L.
(2)以a为直径的圆的面积为S1==π.
把AB分成两条相等的线段,每个小圆的面积S2==π=S1;
把AB分成三条相等的线段,每个小圆的面积S3==π=S1;
把AB分成四条相等的线段,每个小圆的面积S4==π=S1;
把AB分成n条相等的线段,每个小圆的面积Sn=S1.
21.解:∵正方形ABCD的边长为1,
∴扇形的半径分别为1,2,3,4,圆心角为90°,
∴S阴影=π×12+π×22+π×32+π×42
=π+π+π+4π
=π.
圆的初步认识》单元测试卷
一.选择题
1.一个扇形的圆心角为120°,半径为3,则这个扇形的面积是( )
A.π
B.2π
C.3π
D.4π
2.下列说法中,正确的是( )
A.弦是直径
B.半圆是弧
C.过圆心的线段是直径
D.圆心相同半径相同的两个圆是同心圆
3.下列说法错误的是( )
A.直径是圆中最长的弦
B.长度相等的两条弧是等弧
C.面积相等的两个圆是等圆
D.半径相等的两个半圆是等弧
4.如图,⊙O中,点A,O,D以及点B,O,C分别在一条直线上,图中弦的条数有( )
A.2条
B.3条
C.4条
D.5条
5.到圆心的距离不大于半径的点的集合是( )
A.圆的外部
B.圆的内部
C.圆
D.圆的内部和圆
6.如图所示,MN为⊙O的弦,∠N=50°,则∠MON的度数为( )
A.40°
B.50°
C.80°
D.100°
7.如图,AB是半圆的直径,AB=2r,C、D为半圆的三等分点,则图中阴影部分的面积是( )
A.
B.
C.
D.
8.如图,在扇形OAB中,已知∠AOB=90°,OA=,过的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为( )
A.π﹣1
B.﹣1
C.π﹣
D.﹣
二.填空题
9.到点O的距离等于8的点的集合是
.
10.已知⊙O的半径为5cm,则圆中最长的弦长为
cm.
11.已知⊙O中最长的弦为16cm,则⊙O的半径为
cm.
12.已知一个扇形的半径为6cm,圆心角为120°,则这个扇形的面积为
cm2.
13.点A、B在⊙O上,若∠AOB=40°,则∠OAB=
.
14.如图,在扇形OAB中,已知∠AOB=90°,OA=,过弧AB的中点C作CD⊥OA,CE⊥OB,垂足分别为D、E,则图中阴影部分的面积为
.
15.如图在以点O为圆心的两个同心圆中,大圆的半径为2,小圆的半径为1,∠AOB=100°.则阴影部分的面积是
.
16.如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是
.
三.解答题
17.一个扇形的圆心角60°,半径为12cm,求它的面积.(保留π)
18.如图,圆心为点M的三个半圆的直径都在x轴上,所有标注A的图形面积都是SA,所有标注B的图形面积都是SB.
(1)求标注C的图形面积SC;
(2)求SA:SB.
19.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长l=πa.
计算:(1)把AB分成两条相等的线段,每个小圆的周长;
(2)把AB分成三条相等的线段,每个小圆的周长l3=
;
(3)把AB分成四条相等的线段,每个小圆的周长l4=
;
(4)把AB分成n条相等的线段,每个小圆的周长ln=
.
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的
.请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
20.如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长L=πa.
(1)计算:①把AB分成两条相等的线段,每个小圆的周长
;
②把AB分成三条相等的线段,每个小圆的周长L3=
;
③把AB分成四条相等的线段,每个小圆的周长L4=
;
…
④把AB分成n条相等的线段,每个小圆的周长Ln=
;
(2)请仿照上面的探索方法和步骤,计算并导出:当把大圆直径平均分成n等分时,以每条线段为直径画小圆,那么每个小圆的面积Sn与大圆的面积S的关系是:Sn=
S.
21.如图所示,正方形ABCD的边长为1,依次以A,B,C,D为圆心,以AD,BE,CF,DG为半径画扇形,求阴影部分的面积.
参考答案与试题解析
一.选择题
1.解:这个扇形的面积==3π.
故选:C.
2.解:A、直径是弦,但弦不一定是直径,故错误;
B、半圆是弧,正确;
C、过圆心的弦是直径,故错误;
D、圆心相同半径不同的两个圆是同心圆,故错误,
故选:B.
3.解:A、直径是圆中最长的弦,所以A选项的说法正确;
B、在同圆或等圆中,长度相等的两条弧是等弧,所以B选项的说法错误;
C、面积相等的两个圆的半径相等,则它们是等圆,所以C选项的说法正确;
D、半径相等的两个半圆是等弧,所以D选项的说法正确.
故选:B.
4.解:图中的弦有AB,BC,CE共三条,
故选:B.
5.解:根据点和圆的位置关系,知圆的内部是到圆心的距离小于的所有点的集合;
圆是到圆心的距离等于半径的所有点的集合.
所以与圆心的距离不大于半径的点所组成的图形是圆的内部(包括边界).
故选:D.
6.解:∵OM=ON,
∴∠M=∠N=50°,
∴∠MON=180°﹣2×50°=80°.
故选:C.
7.解:连接OC、OD.
∵△COD和△CDA等底等高,
∴S△COD=S△ACD.
∵点C,D为半圆的三等分点,AB=2r,
∴∠COD=180°÷3=60°,OA=r,
∴阴影部分的面积=S扇形COD==πr2.
故选:B.
8.解:∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=∠AOB=90°,
∴四边形CDOE是矩形,
连接OC,
∵点C是的中点,
∴∠AOC=∠BOC,
∵OC=OC,
∴△COD≌△COE(AAS),
∴OD=OE,
∴矩形CDOE是正方形,
∵OC=OA=,
∴OE=1,
∴图中阴影部分的面积=﹣1×1=﹣1,
故选:B.
二.填空题
9.解:到点O的距离等于8的点的集合是:以点O为圆心,以8为半径的圆.
故答案是:以点O为圆心,以8为半径的圆.
10.解:∵⊙O的半径为5cm,
∴⊙O的直径为10cm,
即圆中最长的弦长为10cm.
故答案为10.
11.解:∵⊙O中最长的弦为16cm,即直径为16cm,
∴⊙O的半径为8cm.
故答案为:8.
12.解:∵r=6cm,n=120°,
根据扇形的面积公式S=得
S扇==12(cm2).
故答案为:12π.
13.解:如图,
∵∠AOB=40°,OA=OB,
∴∠OAB=∠OBA==70°,
故答案为:70°.
14.解:∵CD⊥OA,CE⊥OB,
∴∠CDO=∠CEO=∠AOB=90°,
∴四边形CDOE是矩形,
连接OC,
∵点C是弧AB的中点,
∴∠AOC=∠BOC,
∵OC=OC,
∴△COD≌△COE(AAS),
∴OD=OE,
∴矩形CDOE是正方形,
∵OC=OA=,
∴OE=1,
∴图中阴影部分的面积=﹣1×1=﹣1,
故答案为﹣1.
15.解:S阴影=﹣=π,
故答案为π.
16.解:由AB=OC,得
AB=OB,
∠A=∠AOB.
由BO=EO,得
∠BEO=∠EBO.
由∠EBO是△ABO的外角,得
∠EBO=∠A+∠AOB=2∠A,
∠BEO=∠EBO=2∠A.
由∠DOE是△AOE的外角,得
∠A+∠AEO=∠EOD,
即∠A+2∠A=84°,
∠A=28°.
故答案为:28°.
三.解答题
17.解:由扇形面积公式得:S==24π(cm2),
故扇形的面积为:24πcm2.
18.解:(1)由题意得到圆M的半径为(6﹣4)÷2=1,
则.(1分)
(2)
∴(3分)
∵
∴(5分)
∴
即SA:SB=5:6(6分)
19.解:(2)l;
(3)l;
(4)l;;
每个小圆面积=π(?a)2=?,而大圆的面积=π(?a)2=πa2
即每个小圆的面积是大圆的面积的.
20.解:(1)根据L=πd,
①把AB分成两条相等的线段,每个小圆的周长L2=a=L;
②把AB分成三条相等的线段,每个小圆的周长L3=a=L,
③把AB分成四条相等的线段,每个小圆的周长L4=a=L;
④把AB分成n条相等的线段,每个小圆的周长Ln=a=L.
(2)以a为直径的圆的面积为S1==π.
把AB分成两条相等的线段,每个小圆的面积S2==π=S1;
把AB分成三条相等的线段,每个小圆的面积S3==π=S1;
把AB分成四条相等的线段,每个小圆的面积S4==π=S1;
把AB分成n条相等的线段,每个小圆的面积Sn=S1.
21.解:∵正方形ABCD的边长为1,
∴扇形的半径分别为1,2,3,4,圆心角为90°,
∴S阴影=π×12+π×22+π×32+π×42
=π+π+π+4π
=π.
