六年级下册数学课件 4.7 面积的变化 苏教版(共18张PPT)
文档属性
| 名称 | 六年级下册数学课件 4.7 面积的变化 苏教版(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-19 22:06:14 | ||
图片预览




文档简介
(共18张PPT)
面
积
的
变
化
3cm
2cm
9cm
6cm
3cm
2cm
9cm
6cm
3cm
2cm
9cm
6cm
【活动素材一】
验证:
结论:大长方形与小长方形对应边的比是(
):(
),面积的比是(
):(
)。
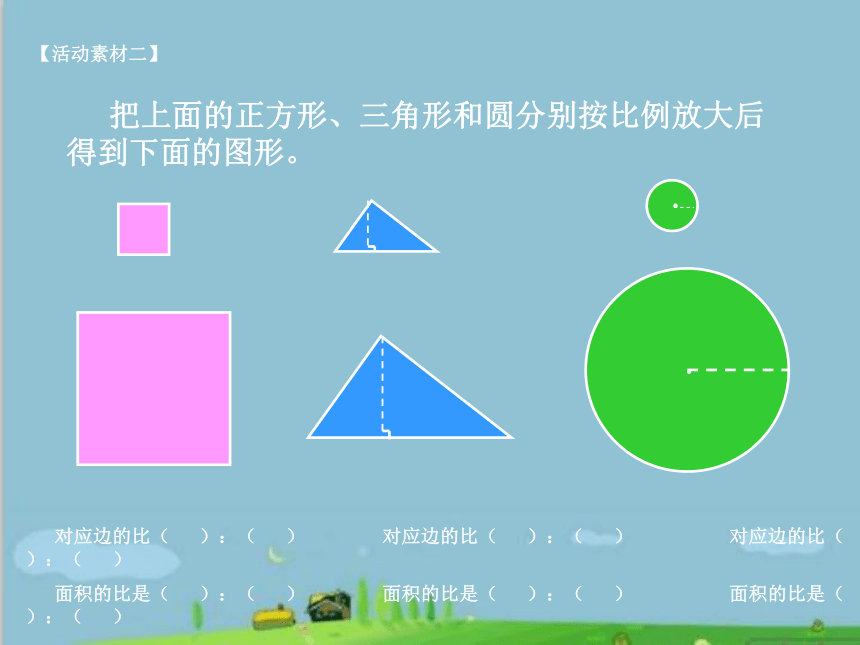
把上面的正方形、三角形和圆分别按比例放大后
得到下面的图形。
【活动素材二】
对应边的比(
):(
)
对应边的比(
):(
)
对应边的比(
):(
)
面积的比是(
):(
)
面积的比是(
):(
)
面积的比是(
):(
)
1、量出相关数据(将数据标记在图上)。
2、写出放大后与放大前对应边的比及面积的比。
(将数据填入相应的括号里)
3、比较每个图形放大后与放大前对应边的比
和面积的比,看你有什么新的发现?把你的
发现和小组的同学说一说。
【活动要求】
1cm
3cm
2cm
0.5cm
4cm
2cm
2cm
1cm
把上面的正方形、三角形和圆分别按比例放大后
得到下面的图形。
选择自己喜欢的方法(
“画”
“算”
),验证平行四边形按比例放大后面积的变化,看看是否符合上面发现的规律。
我用的是(
)方法,将一个平行四边形按(
):(
)放大后,对应边的比是(
):(
),面积的比是(
):(
)。
【活动素材三】
=
π
×
r
×
r
S三
=
a
×
h
÷
2
扩大2倍
扩大2倍
扩大(2
×2)倍
=
22
倍
S圆
=
π
×
r
2
扩大4倍
扩大4倍
扩大(4
×4)倍
=
42
倍
回顾反思
如果一个平面图形按
1:n
缩小,缩小后与缩小前
面积的比是(
)
。
如果两个平面图形对应边长的比是
n:m
,这两个
图形面积的比是(
)。
1
:
n2
n2
:
m2
如果一个立体图形按
n:1
放大,放大后与放大前
体积的比是(
)
。
n3
:
1
如果一个平面图形按
1:n
缩小,缩小后与缩小前
面积的比是(
)
。
如果两个平面图形对应边长的比是
n:m
,这两个
图形面积的比是(
)。
如果一个立体图形按n:1放大,放大后与放大前
体积的比是(
)
。
1
:
n2
n2
:
m2
n3
:
1
推
算
画
验证
如果一个平面图形按
1:n
缩小,缩小后与缩小前
面积的比是(
)
。
如果两个平面图形对应边长的比是
n:m
,这两个
图形面积的比是(
)。
如果一个立体图形按n:1放大,放大后与放大前
体积的比是(
)
。
1
:
n2
n2
:
m2
n3
:
1
推
算
画
猜想
验证
结论
3、
一个长方形按
3:
1
的比放大,原来长方形的
面积是8平方厘米,那么放大后长方形的面积是
(
)平方厘米。
4、两个圆半径的比是
2
:
1
,面积的比是(
),
周长的(
)。
2、如果一个三角形放大后的面积与原面积的比是
25
:1,那么这个三角形是按(
)
:
(
)放大的。
72
5
1
4
:
1
2:
1
1、把一个梯形按
6
:
1
的比放大,放大后的面积
与原面积的比是(
)。
36
:
1
图形按3:1放大,面积的比是9:1。放大后的面积是原面积的9倍。8×9=72(平方厘米)
面
积
的
变
化
3cm
2cm
9cm
6cm
3cm
2cm
9cm
6cm
3cm
2cm
9cm
6cm
【活动素材一】
验证:
结论:大长方形与小长方形对应边的比是(
):(
),面积的比是(
):(
)。
把上面的正方形、三角形和圆分别按比例放大后
得到下面的图形。
【活动素材二】
对应边的比(
):(
)
对应边的比(
):(
)
对应边的比(
):(
)
面积的比是(
):(
)
面积的比是(
):(
)
面积的比是(
):(
)
1、量出相关数据(将数据标记在图上)。
2、写出放大后与放大前对应边的比及面积的比。
(将数据填入相应的括号里)
3、比较每个图形放大后与放大前对应边的比
和面积的比,看你有什么新的发现?把你的
发现和小组的同学说一说。
【活动要求】
1cm
3cm
2cm
0.5cm
4cm
2cm
2cm
1cm
把上面的正方形、三角形和圆分别按比例放大后
得到下面的图形。
选择自己喜欢的方法(
“画”
“算”
),验证平行四边形按比例放大后面积的变化,看看是否符合上面发现的规律。
我用的是(
)方法,将一个平行四边形按(
):(
)放大后,对应边的比是(
):(
),面积的比是(
):(
)。
【活动素材三】
=
π
×
r
×
r
S三
=
a
×
h
÷
2
扩大2倍
扩大2倍
扩大(2
×2)倍
=
22
倍
S圆
=
π
×
r
2
扩大4倍
扩大4倍
扩大(4
×4)倍
=
42
倍
回顾反思
如果一个平面图形按
1:n
缩小,缩小后与缩小前
面积的比是(
)
。
如果两个平面图形对应边长的比是
n:m
,这两个
图形面积的比是(
)。
1
:
n2
n2
:
m2
如果一个立体图形按
n:1
放大,放大后与放大前
体积的比是(
)
。
n3
:
1
如果一个平面图形按
1:n
缩小,缩小后与缩小前
面积的比是(
)
。
如果两个平面图形对应边长的比是
n:m
,这两个
图形面积的比是(
)。
如果一个立体图形按n:1放大,放大后与放大前
体积的比是(
)
。
1
:
n2
n2
:
m2
n3
:
1
推
算
画
验证
如果一个平面图形按
1:n
缩小,缩小后与缩小前
面积的比是(
)
。
如果两个平面图形对应边长的比是
n:m
,这两个
图形面积的比是(
)。
如果一个立体图形按n:1放大,放大后与放大前
体积的比是(
)
。
1
:
n2
n2
:
m2
n3
:
1
推
算
画
猜想
验证
结论
3、
一个长方形按
3:
1
的比放大,原来长方形的
面积是8平方厘米,那么放大后长方形的面积是
(
)平方厘米。
4、两个圆半径的比是
2
:
1
,面积的比是(
),
周长的(
)。
2、如果一个三角形放大后的面积与原面积的比是
25
:1,那么这个三角形是按(
)
:
(
)放大的。
72
5
1
4
:
1
2:
1
1、把一个梯形按
6
:
1
的比放大,放大后的面积
与原面积的比是(
)。
36
:
1
图形按3:1放大,面积的比是9:1。放大后的面积是原面积的9倍。8×9=72(平方厘米)
