2020-2021学年人教版数学八年级上册13.3.2 等边三角形课件(14张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册13.3.2 等边三角形课件(14张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 16:54:43 | ||
图片预览



文档简介
A
B
C
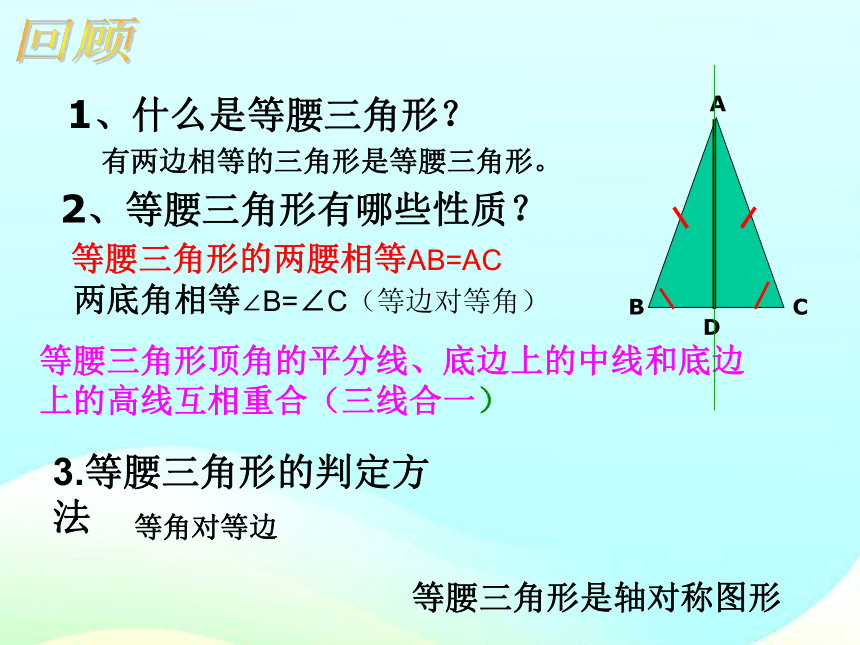
1、什么是等腰三角形?
2、等腰三角形有哪些性质?
等腰三角形的两腰相等AB=AC
两底角相等∠B=∠C(等边对等角)
等腰三角形顶角的平分线、底边上的中线和底边上的高线互相重合(三线合一)
D
等腰三角形是轴对称图形
有两边相等的三角形是等腰三角形。
3.等腰三角形的判定方法
等角对等边
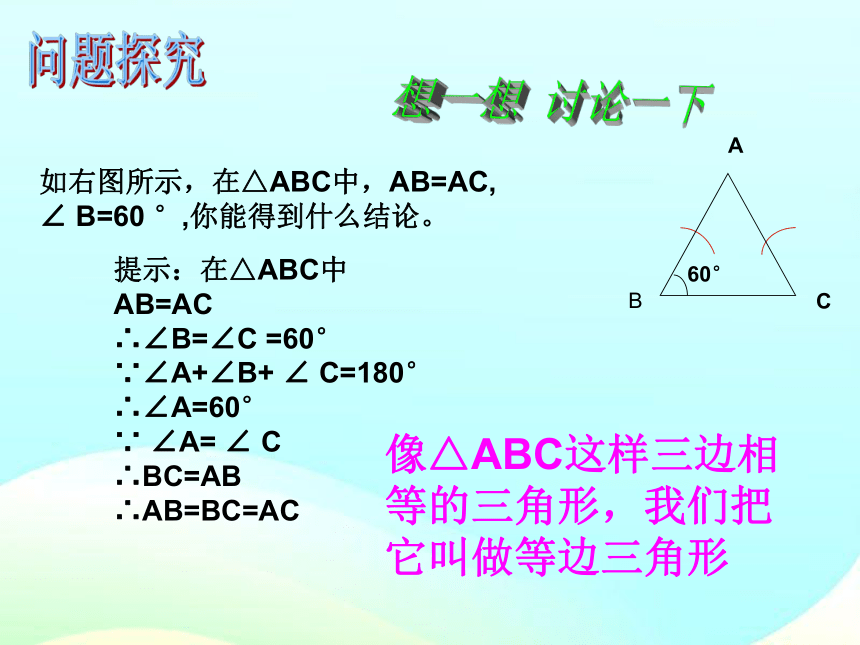
如右图所示,在△ABC中,AB=AC, ∠ B=60 °,你能得到什么结论。
A
B
C
提示:在△ABC中AB=AC
∴∠B=∠C =60°
∵∠A+∠B+ ∠ C=180°
∴∠A=60°
∵ ∠A= ∠ C
∴BC=AB
∴AB=BC=AC
像△ABC这样三边相等的三角形,我们把它叫做等边三角形
60°
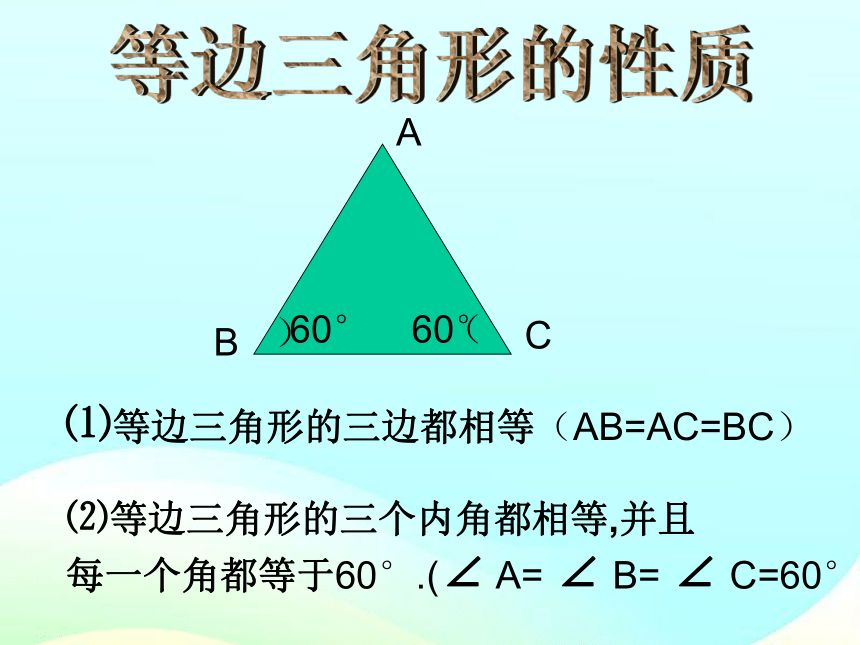
⑵等边三角形的三个内角都相等,并且
每一个角都等于60°.(∠ A= ∠ B= ∠ C=60°)
⑴等边三角形的三边都相等(AB=AC=BC)
A
B
C
)
(
60°
60°
等边三角形是轴对称图形吗?
若是,有几条对称轴?
结论:等边三角形是轴对称图形,
有三条对称轴.
等边三角形性质探索:
思考题
?
一个三角形满足什么条件
就是等边三角形?
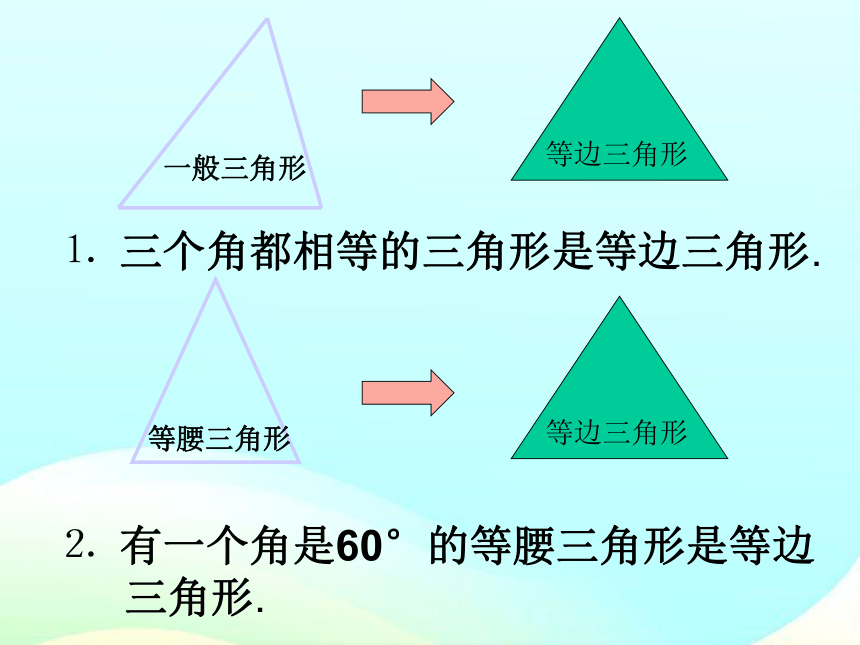
一般三角形
等边三角形
⒈ 三个角都相等的三角形是等边三角形.
⒉ 有一个角是60°的等腰三角形是等边
三角形.
等边三角形
等腰三角形
1.三个内角都相等的三角形是等边三角形.
∵∠A=∠B=∠C=60 °
∴AB=AC=BC (等角对等边)
∴三角形△ABC是等边三角形.
等边三角形判定探索(判定方法):
A
B
C
有一个内角等于60 °的等腰三角形是什么三角形?
假若AB=AC.则∠ B= ∠ C
1.当顶角∠A=60 °时,∠ B= ∠ C= 60 °
∴ ∠A= ∠ B= ∠ C=60 °
∴ △ABC是等边三角形.
2.当底角∠ B= 60时,∠ C=60 °,
∠A=180 -(60 °+60 °)=60. °
∴ ∠A= ∠ B= ∠ C=60 °
∴ △ABC是等边三角形.
A
B
C
等边三角形判定探索:
等边三角形判定方法2:
有一个内角等于60 °的等腰三角形是等边三角形
A
B
C
怎样判断三角形ABC是等边三角形?
方法一:三角形的三边相等;
方法三:有一个角等于60°的等腰三角形 是等边三角形。
方法二:三角形的三角相等;
例:如图12.3-7,⊿ABC是等边三角形,DE∥BC,交AB、AC于D、E,
求证: ⊿ADE是等边三角形。
∵ ⊿ABC是等边三角形,
∴∠A=∠B=∠C
∴∠ADE=∠B,∠AED=∠C
∴∠A=∠ADE=∠AED
∴⊿ADE是等边三角形
A
B
C
D
E
如图12.3-7
∵ DE∥BC
证明:
练习
A
B
C
E
F
D
1.等边三角形是轴对称图形吗?如 果是,指出它的对称轴.
2.如图,等边三角形⊿ABC中,AD是BC 边上的高,∠BDE=∠CDF=60°图中与BD相等的线段有哪些?
(1).等边三角形的性质.
1.等边三角形的内角都相等,且都等于60 °
2.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形各边上中线,高和所对角的平 分线都三线合一.
(2) 等边三角形的判定:
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
问题探究
在等边三角形ABC的边AB、AC上分别截取AD=AE,?ADE是等边三角形吗?为什么?
A
D
E
B
C
证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60 °.
∵ AD=AE
∴∠ADE=∠AED
∴△ADE是等边三角形
B
C
1、什么是等腰三角形?
2、等腰三角形有哪些性质?
等腰三角形的两腰相等AB=AC
两底角相等∠B=∠C(等边对等角)
等腰三角形顶角的平分线、底边上的中线和底边上的高线互相重合(三线合一)
D
等腰三角形是轴对称图形
有两边相等的三角形是等腰三角形。
3.等腰三角形的判定方法
等角对等边
如右图所示,在△ABC中,AB=AC, ∠ B=60 °,你能得到什么结论。
A
B
C
提示:在△ABC中AB=AC
∴∠B=∠C =60°
∵∠A+∠B+ ∠ C=180°
∴∠A=60°
∵ ∠A= ∠ C
∴BC=AB
∴AB=BC=AC
像△ABC这样三边相等的三角形,我们把它叫做等边三角形
60°
⑵等边三角形的三个内角都相等,并且
每一个角都等于60°.(∠ A= ∠ B= ∠ C=60°)
⑴等边三角形的三边都相等(AB=AC=BC)
A
B
C
)
(
60°
60°
等边三角形是轴对称图形吗?
若是,有几条对称轴?
结论:等边三角形是轴对称图形,
有三条对称轴.
等边三角形性质探索:
思考题
?
一个三角形满足什么条件
就是等边三角形?
一般三角形
等边三角形
⒈ 三个角都相等的三角形是等边三角形.
⒉ 有一个角是60°的等腰三角形是等边
三角形.
等边三角形
等腰三角形
1.三个内角都相等的三角形是等边三角形.
∵∠A=∠B=∠C=60 °
∴AB=AC=BC (等角对等边)
∴三角形△ABC是等边三角形.
等边三角形判定探索(判定方法):
A
B
C
有一个内角等于60 °的等腰三角形是什么三角形?
假若AB=AC.则∠ B= ∠ C
1.当顶角∠A=60 °时,∠ B= ∠ C= 60 °
∴ ∠A= ∠ B= ∠ C=60 °
∴ △ABC是等边三角形.
2.当底角∠ B= 60时,∠ C=60 °,
∠A=180 -(60 °+60 °)=60. °
∴ ∠A= ∠ B= ∠ C=60 °
∴ △ABC是等边三角形.
A
B
C
等边三角形判定探索:
等边三角形判定方法2:
有一个内角等于60 °的等腰三角形是等边三角形
A
B
C
怎样判断三角形ABC是等边三角形?
方法一:三角形的三边相等;
方法三:有一个角等于60°的等腰三角形 是等边三角形。
方法二:三角形的三角相等;
例:如图12.3-7,⊿ABC是等边三角形,DE∥BC,交AB、AC于D、E,
求证: ⊿ADE是等边三角形。
∵ ⊿ABC是等边三角形,
∴∠A=∠B=∠C
∴∠ADE=∠B,∠AED=∠C
∴∠A=∠ADE=∠AED
∴⊿ADE是等边三角形
A
B
C
D
E
如图12.3-7
∵ DE∥BC
证明:
练习
A
B
C
E
F
D
1.等边三角形是轴对称图形吗?如 果是,指出它的对称轴.
2.如图,等边三角形⊿ABC中,AD是BC 边上的高,∠BDE=∠CDF=60°图中与BD相等的线段有哪些?
(1).等边三角形的性质.
1.等边三角形的内角都相等,且都等于60 °
2.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形各边上中线,高和所对角的平 分线都三线合一.
(2) 等边三角形的判定:
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
问题探究
在等边三角形ABC的边AB、AC上分别截取AD=AE,?ADE是等边三角形吗?为什么?
A
D
E
B
C
证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60 °.
∵ AD=AE
∴∠ADE=∠AED
∴△ADE是等边三角形
