2020-2021学年人教版数学八年级上册13.4课题学习最短路径问题 课件(张PPT)
文档属性
| 名称 | 2020-2021学年人教版数学八年级上册13.4课题学习最短路径问题 课件(张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 215.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-20 17:14:56 | ||
图片预览



文档简介
13.4 最短路径问题
第13章 轴对称
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
前 言
学习目标
1、能利用轴对称解决简单的最短路径问题。
2、在谈最短路径的过程中,体会“轴对称”桥梁作用,感悟转化的数学思想。
重点难点
重点:利用轴对称将最短路径问题转化为“两点之间,线段最短”问题。
难点:如何利用轴对称将最短路径问题转化为线段和最小问题。
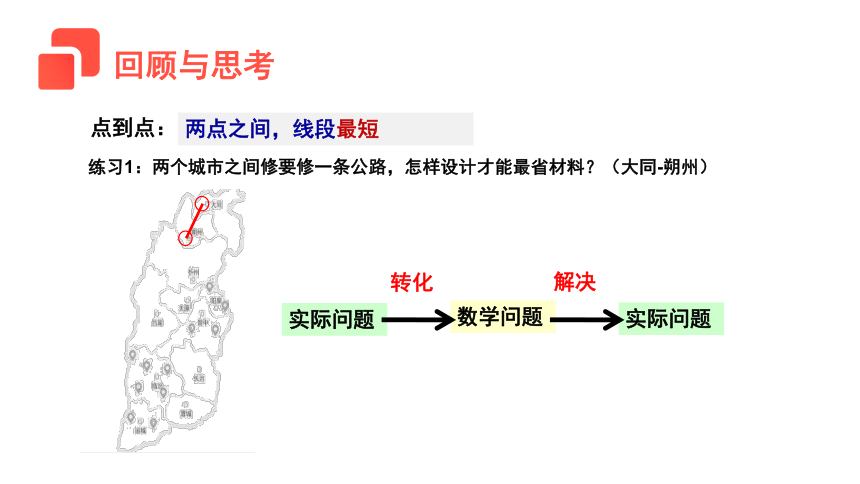
点到点:
两点之间,线段最短
练习1:两个城市之间修要修一条公路,怎样设计才能最省材料?(大同-朔州)
实际问题
数学问题
实际问题
转化
解决
回顾与思考
如图,从A点到B点有三条线路,哪条最短?为什么?
测试
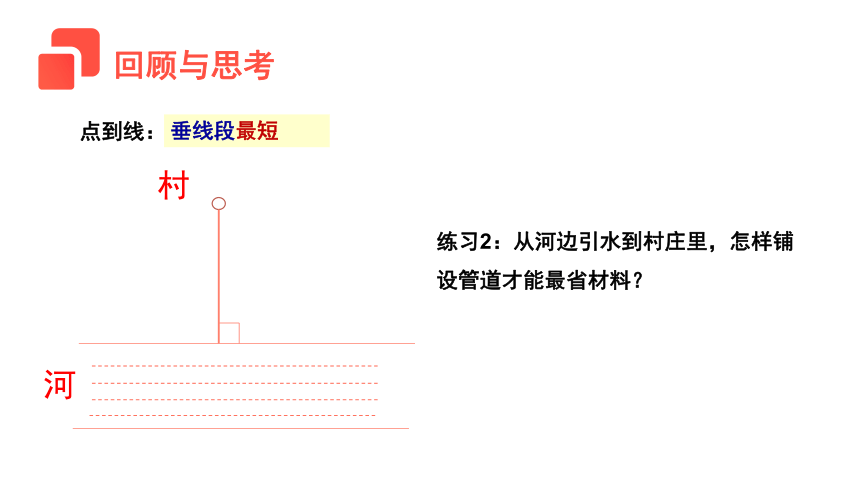
点到线:
垂线段最短
练习2:从河边引水到村庄里,怎样铺设管道才能最省材料?
河
村
回顾与思考
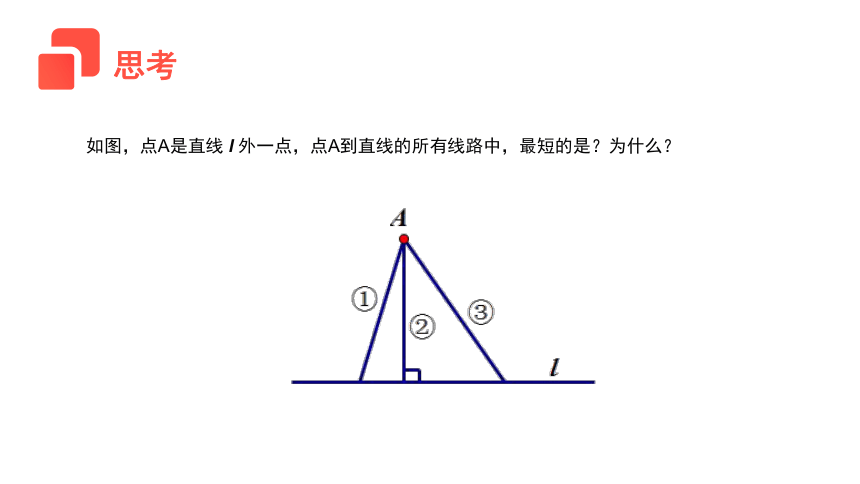
如图,点A是直线 l 外一点,点A到直线的所有线路中,最短的是?为什么?
思考
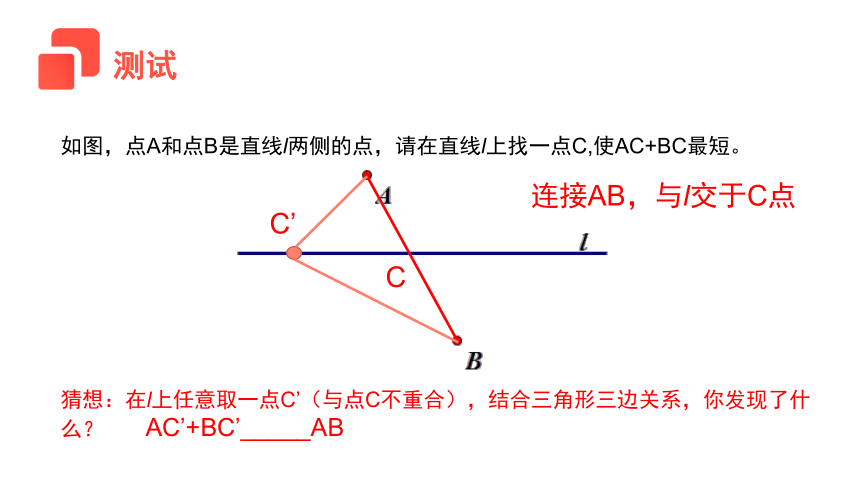
如图,点A和点B是直线l两侧的点,请在直线l上找一点C,使AC+BC最短。
C
C’
连接AB,与l交于C点
猜想:在l上任意取一点C’(与点C不重合),结合三角形三边关系,你发现了什么? AC’+BC’_____AB
测试
从图中的A地出发,到一条笔直的河边l饮马,然后到B地.河边饮马点C在河边什么地方可使他所走的路线全程最短?
B
A
l
这是一个实际问题,你打算首先做什么?
转化为数学问题
探究
将A,B 两地抽象为两个点,将河l 抽象为一条直线.
B
·
·
A
l
在直线l上找一点C,
使AC+BC最短
猜想一下,点C的位置会在哪呢?
在练习纸上尝试画出?
你能用自己的语言
把问题抽象为数学问题吗?
探究
B
·
·
A
l
作法:
作点B 关于直线l 的对称点B′;
连接AB′,与直线l 相交于点C.
则点C 即为所求.
B’
C
画法
B
·
·
A
l
B’
C
C’
在l上任取另一点C’(与点C不重合),
连结BC’、AC’、B’C’
证明:
∴BC+AC=B’C+AC=AB’ .
∴BC’+AC’=B’C’+AC’
∵直线l是点B、B’的对称轴,
点C、C’在对称轴上,
在△AB’C’中,AC’+B’C’ >AB’
即:AC’+BC’ >AC+BC
∴BC=B’C, BC’=B’C’.
验证
如图,A和B两地在一条河的两岸,现要在河上造一座桥MN.桥造在何处才能使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
B
A
探究
B
A
如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN,那么怎样确定什么情况下最短呢?
M
N
探究
解:如图,平移A到A1,使AA1等于河宽,连接A1B交河岸于N作桥MN,此时路径AM+MN+BN最短.
B
A
A1
M
N
猜想
B
A
A1
M
N
理由;另任作桥M1N1,连接AM1,BN1,A1N1.
N1
M1
由平移性质可知,AM=A1N,AA1=MN=M1N1,AM1=A1N1.
AM+MN+BN转化为AA1+A1B,而AM1+M1N1+BN1 转化为AA1+A1N1+BN1.
在△A1N1B中,由线段公理知A1N1+BN1>A1B
因此AM1+M1N1+BN1> AM+MN+BN
验证
解决最短路径问题的基本步骤:
1.实际问题---数学问题(点、线)
2.未知---已知
3.利用轴对称变换和平移变化
4.根据“两点之间,线段最短”,确定最短路径
总结
感谢各位的仔细聆听
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
第13章 轴对称
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
前 言
学习目标
1、能利用轴对称解决简单的最短路径问题。
2、在谈最短路径的过程中,体会“轴对称”桥梁作用,感悟转化的数学思想。
重点难点
重点:利用轴对称将最短路径问题转化为“两点之间,线段最短”问题。
难点:如何利用轴对称将最短路径问题转化为线段和最小问题。
点到点:
两点之间,线段最短
练习1:两个城市之间修要修一条公路,怎样设计才能最省材料?(大同-朔州)
实际问题
数学问题
实际问题
转化
解决
回顾与思考
如图,从A点到B点有三条线路,哪条最短?为什么?
测试
点到线:
垂线段最短
练习2:从河边引水到村庄里,怎样铺设管道才能最省材料?
河
村
回顾与思考
如图,点A是直线 l 外一点,点A到直线的所有线路中,最短的是?为什么?
思考
如图,点A和点B是直线l两侧的点,请在直线l上找一点C,使AC+BC最短。
C
C’
连接AB,与l交于C点
猜想:在l上任意取一点C’(与点C不重合),结合三角形三边关系,你发现了什么? AC’+BC’_____AB
测试
从图中的A地出发,到一条笔直的河边l饮马,然后到B地.河边饮马点C在河边什么地方可使他所走的路线全程最短?
B
A
l
这是一个实际问题,你打算首先做什么?
转化为数学问题
探究
将A,B 两地抽象为两个点,将河l 抽象为一条直线.
B
·
·
A
l
在直线l上找一点C,
使AC+BC最短
猜想一下,点C的位置会在哪呢?
在练习纸上尝试画出?
你能用自己的语言
把问题抽象为数学问题吗?
探究
B
·
·
A
l
作法:
作点B 关于直线l 的对称点B′;
连接AB′,与直线l 相交于点C.
则点C 即为所求.
B’
C
画法
B
·
·
A
l
B’
C
C’
在l上任取另一点C’(与点C不重合),
连结BC’、AC’、B’C’
证明:
∴BC+AC=B’C+AC=AB’ .
∴BC’+AC’=B’C’+AC’
∵直线l是点B、B’的对称轴,
点C、C’在对称轴上,
在△AB’C’中,AC’+B’C’ >AB’
即:AC’+BC’ >AC+BC
∴BC=B’C, BC’=B’C’.
验证
如图,A和B两地在一条河的两岸,现要在河上造一座桥MN.桥造在何处才能使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
B
A
探究
B
A
如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN,那么怎样确定什么情况下最短呢?
M
N
探究
解:如图,平移A到A1,使AA1等于河宽,连接A1B交河岸于N作桥MN,此时路径AM+MN+BN最短.
B
A
A1
M
N
猜想
B
A
A1
M
N
理由;另任作桥M1N1,连接AM1,BN1,A1N1.
N1
M1
由平移性质可知,AM=A1N,AA1=MN=M1N1,AM1=A1N1.
AM+MN+BN转化为AA1+A1B,而AM1+M1N1+BN1 转化为AA1+A1N1+BN1.
在△A1N1B中,由线段公理知A1N1+BN1>A1B
因此AM1+M1N1+BN1> AM+MN+BN
验证
解决最短路径问题的基本步骤:
1.实际问题---数学问题(点、线)
2.未知---已知
3.利用轴对称变换和平移变化
4.根据“两点之间,线段最短”,确定最短路径
总结
感谢各位的仔细聆听
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear, Concise And Concise Do Not Need Too Much Text
人教版 数学(初中) (八年级 上)
